关于椭圆曲线y2=qx(x2+32)的正整数点

赵建红

(丽江师范高等专科学校 数学与计算机科学系，云南 丽江 674199)



关于椭圆曲线y2=qx(x2+32)的正整数点

赵建红

(丽江师范高等专科学校 数学与计算机科学系，云南 丽江 674199)

设q为无平方因子的正奇数，q的任意素因子qi(i∈Z+)都满足qi≡5(mod 8)，主要利用同余的性质、Legendre符号等证明了y2=qx(x2+32)无正整数点．

椭圆曲线；正整数点；同余；Legendre符号

1 引言及相关结论

椭圆曲线的整数点是数论和算术代数几何学中基本而又重要的问题，关于椭圆曲线y2=qx(x2+a),q,a∈Z+的整数点问题，目前主要结论为：a=1时文献[1-5]已进行了一些研究；a=2时文献[6-10]已进行了一些研究；a=4时，文献[11]已进行了一些研究；a=64时文献[12]进行了一些研究．

本文给出了a=32时椭圆曲线(1)的正整数点的情况．

2 重要引理

引理1[6]对于素数p，方程X2-2p2Y4=1,其中X,Y∈N+仅当p=2和3时分别有解(X,Y)=(3,1)和(17,2)．

3 相关定理

定理1 如果q为无平方因子的正奇数，q的任意素因子qi(i∈Z+)都满足qi≡5(mod 8)，则椭圆曲线

y2=qx(x2+32)

(1)

无正整数点.

证明 设(x,y),x,y∈Z+是椭圆曲线(1)的正整数点，因为q是奇素数，故由椭圆曲线(1)知：q|y，设y=pz，z∈Z+，将其代入椭圆曲线(1)式得：qz2=x(x2+32)

(2)

因为gcd(x,x2+32)=gcd(x,32)=1或2或4或8或16或32，故式(2)可分解为以下6种情况：

情形ix=ma2,x2+32=nb2,z=ab,q=mn,gcd(a,b)=1,a,b∈Z+；

情形iix=2ma2,x2+32=2nb2,z=2ab,q=mn,gcd(a,b)=1,a,b∈Z+；

情形iiix=4ma2,x2+32=4nb2,z=4ab,q=mn,gcd(a,b)=1,a,b∈Z+;

情形ivx=8ma2,x2+32=8nb2,z=8ab,q=mn,gcd(a,b)=1,a,b∈Z+;

情形vx=16ma2,x2+32=16nb2,z=16ab,q=mn,gcd(a,b)=1,a,b∈Z+;

情形vix=32ma2,x2+32=32nb2,z=32ab,q=mn,gcd(a,b)=1,a,b∈Z+.

下面分别讨论这6种情形下椭圆曲线(1)的正整数点的情况.

情形i将x=ma2代入x2+32=nb2,得:

m2a4+32=nb2

(3)

(i)n>1时，n中至少含有一个素因子qj，j∈Z+由题意得qi≡5(mod 8).对式(3)两边同时取模qj，得

(ma2)2≡-32(modqj)

(4)

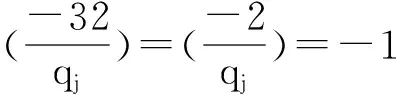
(ii)n=1,m=q此时式(3)成为q2a4+32=b2，两边同时取模q，得：

b2≡-32(modq)

(5)

情形ii将x=2ma2,x2+32=2nb2得：

2m2a4+16=nb2

(6)

(i)n>1时，n中至少含有一个素因子qj，j∈Z+,由题意得qi≡5(mod 8).对式(6)两边同时取模qj，得2m2a4≡-16(modqj)，则有m2a4≡-8(modqj)，即：

(ma2)2≡-8(modqj)

(7)

(ii)n=1时，m=q,此时式(6)成为： 2q2a4+16=b2

(8)

由式(8)知b为偶数，令b=2c(c∈Z+)，整理得：q2a4=2c2-8

(9)

因为b为偶数，而gcd(a,b)=1，所以a为奇数.又q为奇数，故式(9)左边为奇数，右边为偶数，显然不成立，因此n=1时情形ii不成立.

情形iii将x=4ma2代入x2+32=4nb2,得: 4m2a4+8=nb2

(10)

(i)n>1时，n中至少含有一个素因子qj，j∈Z+，由题意得qi≡5(mod 8).对式(10)两边同时取模qj，得4m2a4≡-8(modqj)，则有m2a4≡-2(modqj),即：

(ma2)2≡-2(modqj)

(11)

(ii)n=1时，m=q,此时式(10)成为4q2a4+8=b2，两边同时取模q，得：

b2≡8(modq)

(12)

情形iv将x=8ma2代入x2+32=8nb2,得:

8m2a4+4=nb2

(13)

(i)n>1时，n中至少含有一个素因子qj，j∈Z+，由题意得：qi≡5(mod 8).对式(13)两边同时取模qj，得8m2a4≡-4(modqj)，即4m2a4≡-2(modqj)，也即：

(2ma2)2≡-2(modqj)

(14)

(ii)n=1时，m=q此时式(13)成为:

8q2a4+4=b2

(15)

由式(15)知b为偶数，令b=2c(c∈Z+)，整理得2q2a4+1=c2，两边取模8，得：2q2a4+1≡c2(mod 8)

(16)

因为b为偶数，而gcd(a,b)=1，所以a为奇数，又q为奇数，故2q2a4+1≡3(mod 8)，则由式(16)有c2≡3(mod 8)，显然不成立，因此n=1时情形iv不成立.

情形v将x=16ma2代入x2+32=16nb2得：

16m2a4+2=nb2

(17)

(i)n>1时，n中至少含有一个素因子qj，j∈Z+，由题意得qi≡5(mod 8).对式(17)两边同时取模qj，得16m2a4≡-2(modqj)，即： (4ma2)2≡-2(modqj)

(18)

(ii)n=1时，m=q此时式(17)成为16q2a4+2=b2，两边取模q，得：

b2≡2(modq)

(19)

情形vi将x=32ma2代入x2+32=32nb2,得:

32m2a4+2=nb2

(20)

(i)n>1时，n中至少含有一个素因子qj，j∈Z+，由题意得qi≡5(mod 8).对式(20)两边同时取模qj，得32m2a4≡-1(modqj)，即64m2a4≡-2(modqj)，也即:

(8ma2)2≡-2(modqj)

(21)

(ii)n=1时，m=q此时式(20)成为32q2a4+2=b2，即：

b2-2q2·(2a)4=1

(22)

由引理1知方程(22)仅当q=3时有正整数解(c,2a)=(17,2)，即(c,a)=(17,1)，这与“q≡5(mod 8)为奇素数”矛盾，故n=1时情形vi不成立.

综上有椭圆曲线(1)无正整数点.

[1] 祝辉林，陈建华.两个丢番图方程y2=nx(x2±1)[J].数学学报，2007，50(5)：1071-1074.

[2] 乐茂华.椭圆曲线y2=px(x2±1)的正整数点[J].湛江师范学院学报，2008,29(3)：1-2.

[3] 管训贵.关于椭圆曲线y2=px(x2+1)的一个注记[J].四川理工学院(自然科学版)，2010，23(4)：384,393.

[4] 窦志红.椭圆曲线y2=2px(x2+1)上正整数点的个数[J].纯粹数学与应用数学，2011,27(2)：210-212,235.

[5] 杨海，付瑞琴.一类椭圆曲线有正整数点的判别条件[J].纯粹数学与应用数学，2013,29(4)：338-341.

[6] 廖思泉，乐茂华.椭圆曲线y2=px(x2+2)的正整数点[J].数学杂志，2009,29(3)：387-390.

[7] 陈历敏.Diophantine方程y2=px(x2+2)[J].数学学报，2010,53(1):83-86.

[8] 李玲，张绪绪.椭圆曲线y2=nx(x2+2)的整数点[J].西安工程大学学报，2011，25(3):407-409.

[9] 杜晓英.椭圆曲线y2=nx(x2+2)在p≡1(mod 8)时的正整数点[J].数学的实践与认识,2014,44(15):290-293.

[10] 张瑾.椭圆曲线y2=px(x2+2)有正整数点的判别条件[J].数学的实践与认知，2015,45(4)：232-235.

[11] 崔保军.椭圆曲线y2=px(x2+4)的正整数点[J].佳木斯大学学报(自然科学版)，2014,32(6)：962-963.

[12] 崔保军.椭圆曲线y2=px(x2+64)的正整数点[J].甘肃高师学报，2015,20(2):7-9.

责任编辑：时 凌

The Positive Integral Points on the Elliptic Curvey2=qx(x2+32)

ZHAO Jianhong

(Department of Mathematics and Computer Science, Lijiang teachers college, Lijiang 674199, China)

Letqbe a positive odd number,which has no square factor, and prime factorsqi(i∈Z+) satisfyqi≡5(mod 8).It was proved thaty2=qx(x2+32) has no positive integer points by using some properties of congruence,Legendre symbol.

elliptic curve；positive integer point；congruence；Legendre symbol

2017-03-24.

云南省科技厅应用基础研究计划青年项目 (2013FD061)

赵建红(1981-)，男，硕士，副教授，主要从事初等数论的研究.

1008-8423(2017)02-0134-03

10.13501/j.cnki.42-1569/n.2017.06.004

O156.1

A