超级画板演示初中数学动态问题摭谈
2017-06-21李文录
李文录
(四川省石棉县城北中学)
超级画板演示初中数学动态问题摭谈
李文录
(四川省石棉县城北中学)
超级画板的动画功能是通过自由点和半自由点的运动带动其关联图形变化实现的,其中直线上的点、曲线上的点、多边形边界上的点等半自由点的运动可以进行精确控制,做出可以反映数学动态问题的动画,在教学中可以运用超级画板功能,用不同的方法和技巧制作动画,反映数学现象发生、发展的过程,有利于学生观察、理解、思考,降低动态问题的难度,更有利于学生抽象思维的发展.
超级画板;动画产生;动点控制;动态问题;动画演示
Z+Z智能教育平台——超级画板V2.10功能强大,能够很好地实现中小学数学教学设计的意图,是数学教学和学习的好助手,是数学教育与信息技术整合的一种有力技术手段.笔者接触超级画板的时间短,只见其冰山一角,但也感受到它给数学教育带来的缕缕春风.本文就超级画板演示初中数学动态问题与同行们进行学习、交流.
一、超级画板的动画形式
1.自由点或半自由点的控制动画
直接设置半自由点动画可以使其在所在的几何对象上运动.自由点的动画无规律,直线、射线上的点不容易控制,一般不选取它们作为动画点.
2.将几何对象与运动点关联生成动画
将插入的对象与动画点关联,用点的运动带动关联对象运动.
3.由参数控制图形对象的平移、旋转产生动画效果
坐标轴方向的平移可在平移向量终点坐标上设置参数,然后作这个参数的动画,由参数的范围控制动画.
任意方向上的平移,可在这个方向的直线上先选取两点,再选取第三点,作这个点参数的动画,范围确定在前面两个点的参数之间.
旋转则直接将旋转角设置为变量参数,作这个参数的动画,最大值确定为实际旋转角.
4.由参数控制函数图象变化产生动画效果
输入函数表达式,将函数参数的最大值设置为变量参数,作这个参数的动画,用范围控制图象.
二、超级画板动画的精确控制
1.直线上点的动画的控制
坐标轴上的点可设置坐标参数,直接作点或坐标参数的动画,确定好参数范围,就可以精确控制点的动画.作点A(0,m),作点A(或作参数m)的动画,范围设置为-2~3,点A就在y轴上-2到3之间运动.任意直线上可先选取三点,作其中一点的参数动画,参数范围确定在另两个点的参数之间.点的动画就控制在两点之间.如图1,依次在直线上选取三点H,I,G,作点I参数u001的动画,参数范围u000~u002.点I就在点G和点H之间运动.如果直线是通过表达式作出来的,还可以设直线上一点P(m,k*m+b),作点P或参数m的动画,用自变量范围内的值设定动画参数范围.
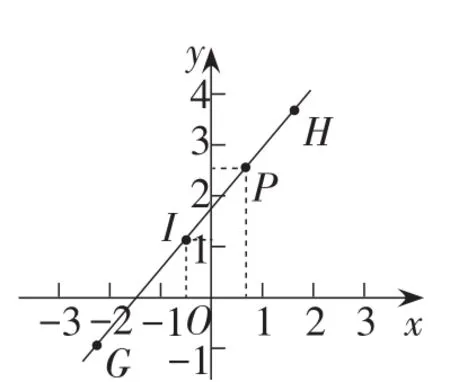
图1
2.曲线上点的动画控制
如图2,圆上的点的动画控制有两种方法.
方法1:直接在圆上选取一点P作动画,用参数范围控制动画,如选取最小值为,最大值为π,点P就在这个范围内运动.
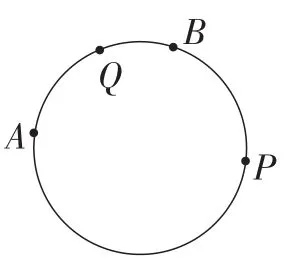
图2
方法2:在圆上选取三点A,B,Q,作其中一点参数的动画,用另外两点的参数为变化范围控制动画.
其他曲线上点的动画控制仍然有两种方法.
方法1:直接在曲线上选取一点作动画,在函数变量的定义域内设置参数范围控制动画.
方法2:在曲线上选取三点,作其中一点参数的动画,用另外两点的参数为变化范围控制动画.
图3中P,Q两点是分别用以上两种方法作的动画,它们在点A和点B之间运动.
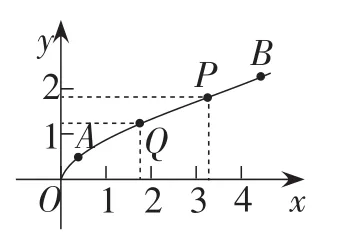
图3
3.多边形边上点的动画控制
方法1:直接作多边形边界上的点,用这个点的参数作动画,设参数变化范围在不超过边数的任意两个值之间,该点将在设定的部分边上运动.如图4,依次选取A,B, C三点,作多边形边界点P,作点P的参数u000的动画,参数范围设为0~2,则点P就在边AB,BC上运动;
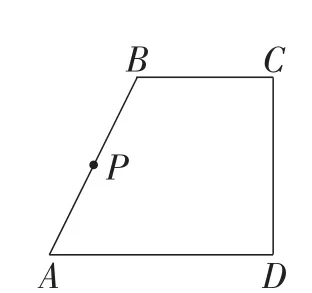
图4
方法2:用含符号函数sign(t,0)的代数式替换边界点的参数u000,X-拖动参数改为t.如图4,用sign(t,0)*sign(2,t)*t/2+(1-sign(2,t))* sign(3,t)*(t-1)+(1-sign(3,t))*2替换边界点的参数u000,X-拖动参数改为t,作参数t的动画,参数范围设为0~2,点P就在边AB,BC上运动.改变参数t的范围则可改变点P的运动路径.
三、超级画板动画技巧在教学中的创造性应用
掌握了超级画板中点的动画方法和技巧,只是制作数学动态问题演示动画的基础,要很好地反映教学中的具体数学动态问题,还要结合实际,灵活运用各种动画技巧,创造性地进行创作,才能达到满意的数学动态问题演示效果.
在公共政策冲突的治理方面,学者们主要从体制、利益关系调整和沟通反馈机制等方面提出对策。具有代表性的观点如改革政策制定体制,加强各政策制定部门的相互协调,做好执行过程的信息反馈工作。除此之外,也要在承认中央与地方利益区别的基础之上,寻找地方利益和中央利益之间的均衡点,协调政策之间的冲突。
例1如图5,△ABC是等边三角形,AB=2,D是BC边的中点,点P从点A出发,沿AB—BD以每秒1个单位长度的速度向终点D运动,同时点Q从点C出发,沿CA—AC以每秒1个单位长度的速度运动,当点P停止运动时,点Q也随之停止运动,设点P运动时间为t秒,△PQD的面积为S.
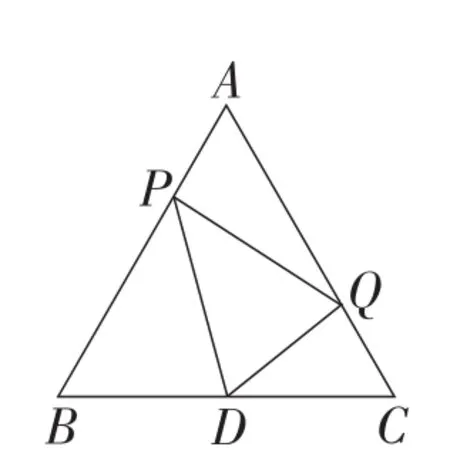
图5
(1)求线段PB的长(用含t的代数式表示);
(2)当△PQD为等边三角形时,求t的值;
(3)当S>0时,求S与t的函数关系式;
(4)若点D关于PQ的对称点为点D′,且S>0,直接写出点D′落在△ABC边上时的t值.
方法1:作AC的中点E,作多边形ABD和多边形
CAE(在超级画板中同一直线上的多个点可以认作多边形,并利用边界上的点作动画)的边界点P,Q,其参数分别为u000,u001,再分别作u000和u001的动画,调整好参数范围,将两动画并行即可.此法容易理解,也容易制作.这里有一技巧值得介绍的是:同一线段上按顺序选取多点可以产生多边形边界上的点,作动画可使其在同一直线上折返运动.
方法2:P,Q的参数u000,u001改为:sign(t,0)* sign(2,t)*t/2+(1-sign(2,t))*sign(3,t)*(t-1)+(1-sign(3,t))*2,X-拖动参数改为t,调整参数范围即可.此法P,Q两点的参数设置复杂,因此这类动态问题一般想到的是用方法1比较恰当.
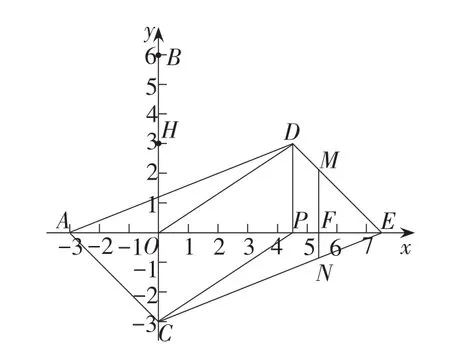
图6
(1)当点C运动到线段OB的中点时,求t的值及点E的坐标;
(2)当点C在线段OB上时,求证:四边形ADEC是平行四边形;
(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在第一、四象限,在运动过程中设▱PCOD的面积为S.
①点M,N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;
②若点M,N中恰好只有一个点落在四边形ADEC的内部(不包括边界)时,直接写出S的取值范围.
作法:设题目描述三个动点分别为P(t,0),C(0,6-2t),E(t+3,0),作参数t的动画,设置参数范围即可.
由于动点P,C在坐标轴上,首先考虑用作动点坐标参数的动画的方法.点P与点C运动的速度和方向都不同,这里用了坐标点的横坐标参数t和纵坐标参数6-2t进行控制.
例3如图7,矩形的长、宽分别为4和3,等腰三角形的底和高分别为3和4,如果此三角形的底和矩形的宽重合,三角形沿矩形宽中点连线所在的直线从左到右匀速穿过矩形,设三角形与矩形重叠部分的面积为S,重叠部分图形的高为x,那么S关于x的函数的大致图象为().

图7
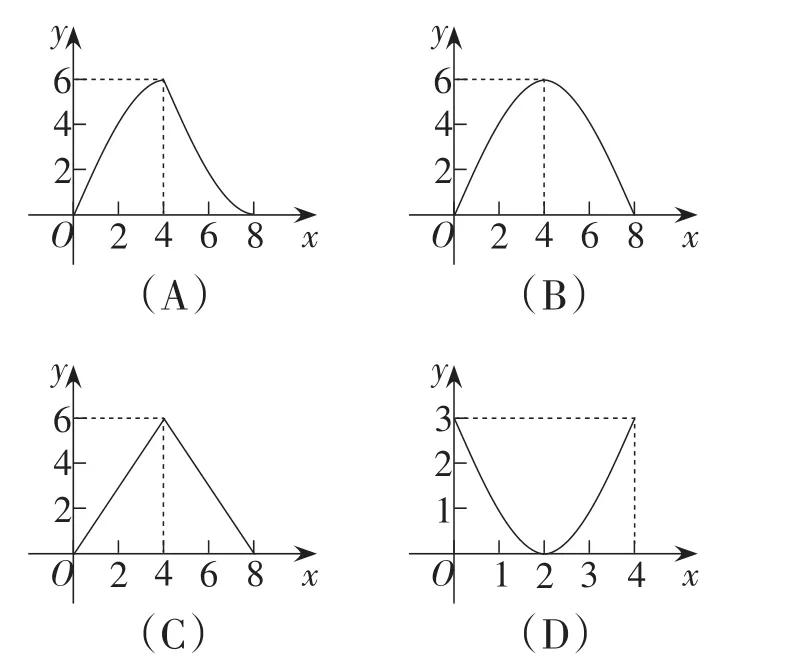
方法1:将等腰三角形的顶点D,E,F的坐标分别设为D(m-4,1.5),E(m,3),F(m,0),作等腰三角形腰与矩形宽的交点,通过作图菜单作如图8、图9所示的多边形EFGH和△DIJ,然后作参数m的动画,范围设置为0~8.用动态Alpha值控制多边形EFGH和△DIJ的显示.
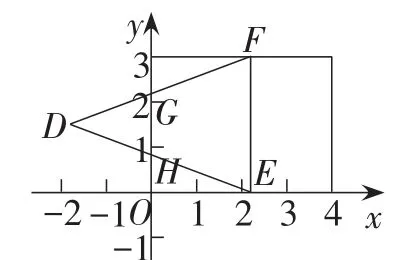
图8

图9
方法2:将△DEF沿x轴方向平移.在x轴上选取两点指定平移向量,其中一点选在起点,另一点设为(m,0),然后作m的动画,参数范围的最小值为起点横坐标的值,最大值为终点横坐标的值,然后将△DEF隐藏.
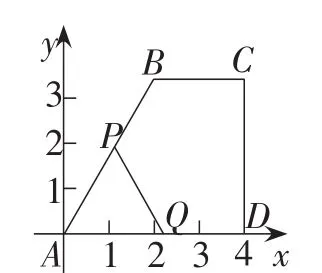
图10
作法:作多边形ABCD的边界点P,其参数为u000,作u000的动画,参数范围设置为0~3,动画的频率设置为100,时间为150毫秒;作线段AD上的点Q,直接作点Q的动画,动画的频率设置为100,时间为50毫秒,同时选中两个动画按钮,启动或停止动画即可.这里主要介绍了通过设置动画时间控制动画的速度.缺点是动画过程与题目实际不相符,两个动画按钮不能并行运动按钮.
从以上例题我们可以看出,用超级画板演示数学动态问题具有明显优势,动画制作是灵活运用超级画板方法和技巧进行创造的过程.
四、数学动态问题演示教学思考
数学动态问题是数学教学的难点,也是学生数学学习的难点,很多学生无法想象数学现象发生、发展的过程,借助超级画板将数学动态问题制作成动画,把数学动态问题直观呈现给学生,让他们从动画中理解数学现象发生、发展的过程,自然就降低了数学动态问题的难度.
学生抽象思维培养需要长期经过从具体数学事实到数学模型,然后才能在大脑中形成抽象的数学概念,对动态数学现象的观察和思考是培养学生抽象思维最好的方法和手段.
通过长期观察动态数学现象,思考变化的数学过程,学生逐步会在大脑中建立动态数学问题的模型,培养学生数学建模的意识和抽象思维的能力.
[1]中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2]张景中.超级画板自由行[M].武汉:湖北科学技术出版社,2016.
[3]叶茂恒,许芬英.2014年中考数学试题“图形的性质”分类解析[J].中国数学教育(初中版),2015(1/2):57-72.
2017—03—16
李文录(1964—),男,中学高级教师,四川省特级教师,四川省初中数学骨干教师,四川省中小学教学名师.主要从事初中教育教学研究.
