开展小学数学建模教学活动的意义与方法

冯远军

【摘要】数学的应用越来越广泛和深入，如何培养学生运用数学知识解决实际问题的能力是数学教学中的一个重要的新课题，数学模型是数学基础知识与数学应用之间的桥梁，数学建模教育不能仅限于高等院校，也应拓展到中小学数学教学方面，小学同样可以开展数学建模的教學活动.

【关键词】数学建模；数学语言；思维创新

数学的方法和应用不只表现在理科方面，已经渗透到各学科各领域中.数学建模教育不能仅限于高等院校，也应拓展到中小学数学教学方面，小学同样可以开展数学建模的教学活动.

一、开展小学数学建模教学活动的意义

数学模型是指用数学符号、公式或图表等语言来刻画某种事物的本质属性与内在规律，一般表现为数学概念、定律、定理、公式、性质、数量关系等.数学模型是数学基础知识与数学应用之间的桥梁，建立和处理数学模型的过程，就是将数学理论知识应用于实际问题的过程；是复杂问题的简化过程；是通过观察和分析实际对象的特征和规律，抓住问题的关键，由数学语言来反映问题的数量关系，然后，利用数学的理论和方法去分析和解决问题的过程.

学生学习数学知识的过程，实际上就是对基本数学模型的学习，是建立数学模型解决实际问题的开始.学生对数学模型的理解、掌握及构建的能力，很大程度上反映了学生的数学思维能力及数学应用能力.

二、开展小学数学建模活动的教学方法

（一）培养学生应用数学知识去分析解决问题的能力

以学习生活中的实际的应用价值出发，选择较感兴趣的问题参与基础知识的教学，把数学建模渗透到数学教学中，可以使学生体会到数学知识与实际问题之间的关系；体会到理论与实践之间的相互作用；体会到数学在学习生活中的地位.小学数学中的计算、整除知识就是广泛被应用的数学知识，教师应多举事例来结合教学，如，学校里班容评分、分组搞游戏、卫生包干区的划分等等的方案设计都可以由学生利用各种不同的运算去构建完成，这样可以直观地为学生阐明了数学的应用价值，从而提高学生学习数学的自觉性.

我们应该改变这种教学观念，充分考虑学生的身心发展特点，对原有的教材内容应进行加工处理，选择与日常生活有关的数学知识作为教学内容，以联系学生的生活实践为基础，使学生体会到数学就在身边，感受到数学的趣味和作用，对数学产生亲切感，吸引学生在学习中主动地去寻找问题和解决问题.

（二）培养学生的数学建模能力

目前小学数学教学的内容较为形式、抽象，只讲概念、定律、推导、计算等，很少讲数学与我们周围世界以及日常生活的密切联系.也许这些教学方法对培养少数数学尖子生还是可以的，但对培养大多数的学生来说欠缺兴趣、欠缺对数学应用的认识，学习确实会有难度，这正是当今的数学教育改革中关键的问题.

适当开设数学建模课，介绍建模活动的过程，通过一些有趣例子来向学生讲授建模的基本方法、步骤.例如，“七桥问题”.

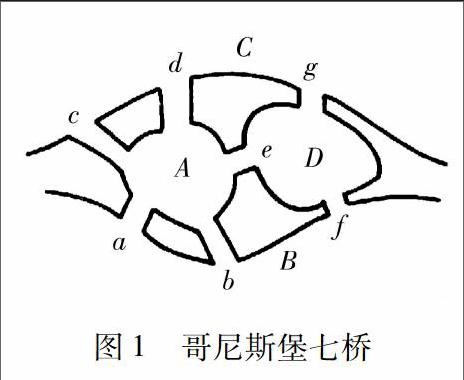
图1哥尼斯堡七桥18世纪，普鲁士哥尼斯堡镇上有一个小岛，岛旁流过一条河的两条支流，七座桥跨在河的两支流上（图1）.

假设A表示岛，B表示河的左岸，C表示右岸，D为两支流间地区，a，b，c，d，e，f，g分别表示七座桥（图1）.

问一个人能否经过每座桥一次且恰好经过每座桥一次并且最后回到原出发点？

图论中最早的问题之一就是“哥尼斯堡七桥问题”.此问题在1736年被欧拉解决之前一直是这个普鲁士城镇中的居民很感兴趣问题.

欧拉解决七桥问题采用了“数学模型”法.

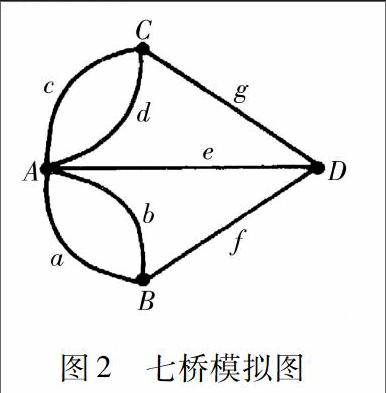
图2七桥模拟图建模既然岛与陆地无非是桥梁连接的，那么就不妨把4处地点缩小（抽象）成4个点，并把7座桥表示（抽象）成7条边，便得到了七桥问题的模拟图（图2），这样当然并未改变问题的实质，于是人们试图一次无重复地走过7座桥的问题就等价于一笔画出上述图形的问题（每条边必须且只需经过一次），此图2就是七桥问题的数学模型.

欧拉解决七桥问题是先考虑一般化问题：如果给定任意一个河道图与任意多座桥，可否判断每座桥能否恰好走过一次呢？一般化的问题就要有一个一般解法，才有更实际的意义，考查一笔画的结构特征，有个起点和终点（若起点和终点重合时即为欧拉图）.除起点与终点处，一笔画中出现在交点处的边总是一进一出的，故交点的度数总和为偶数，由此欧拉给出一般结论：

（1）连接奇数个桥的陆地仅有一个或超过两个以上，不能实现一笔画.

（2）连接奇数个桥的陆地仅有两个时，则从两者任一陆地出发，可以实现一笔画而停在另一陆地.

著名的七桥问题彻底解决了，进一步可知，对于任意一个河道图和任意多座桥的问题都解决了.

【参考文献】

[1]周义仓，等.数学建模实验[M].西安：西安交通大学出版社，1999.

[2]谢云荪，等.数学实验[M].北京：科学出版社，1999.