铁磁元件铁心损耗的低频测量方法

刘 鑫 姚陈果 梁仕斌 王俊凯 刘 涛

(1. 输配电装备及系统安全与新技术国家重点实验室(重庆大学) 重庆 400044 2. 云南电力试验研究院(集团)有限公司 昆明 650051 3. 云南电力技术有限责任公司 昆明 650051)



铁磁元件铁心损耗的低频测量方法

刘 鑫1姚陈果1梁仕斌2王俊凯1刘 涛3

(1. 输配电装备及系统安全与新技术国家重点实验室(重庆大学) 重庆 400044 2. 云南电力试验研究院(集团)有限公司 昆明 650051 3. 云南电力技术有限责任公司 昆明 650051)

变压器出厂实验需要测量其空载励磁特性、空载损耗和负载损耗。空载损耗主要是铁损耗，测量空载损耗时往往要施加一个容量较大的工频电源。为了减小实验电源容量，使测量设备便携化，提出一种采用低频电源代替工频电源测量铁磁元件铁心损耗的低频测量法。该方法通过施加几个频率的低频电压，测量低频下的铁损耗PFe，得到不同频率的E/f(电动势/频率)-PFe曲线，再通过样条插值法计算频率不同、E/f相等时的铁损耗，根据最小二乘原理计算折算至工频下的铁损耗。并在单相变压器和电流互感器中开展实验，采用15,20,25Hz的折算结果与工频50Hz实测结果的相对误差ε<5%，相对误差标准差σε<0.9。结果表明，该方法折算准确度高、稳定性好，并减小了实验电源容量。

铁磁元件 铁心损耗 低频法 最小二乘法 涡流损耗

0 引言

变压器作为电力系统中最重要的输变电设备，其性能好坏直接影响电力系统的安全、经济运行。变压器空载损耗和短路损耗是反映变压器性能的重要参数，不仅反映变压器的运行效率，也反映变压器磁路的局部缺陷和使用寿命。《GB1094.1—2013 电力变压器 第一部分：总则》要求空载损耗和短路损耗测量为例行实验[1]；《JB/T 501—2006电力变压器实验导则》规定，进行空载实验时，应从试品各绕组中的一侧绕组(一般为低压绕组)供给额定频率的额定电压，其余绕组开路[2]。但随着电网电压等级的提高，变压器电压等级和容量也逐渐增大，进行空载实验时所需要的实验设备容量、体积和重量往往很大，导致空载实验程序复杂、操作人员人身安全得不到保障。

铁心损耗的测量、计算在国内外已有较多研究。文献[3]采用低频电源测量铁磁元件伏安特性的补偿算法中考虑了铁心损耗，补偿算法的关键在于对铁心损耗的补偿。文献[4]将铁心损耗分为交变损耗和旋转损耗，有限元仿真计算铁心损耗并与实测值进行了对比。文献[5-8]分析了直流偏磁对变压器铁心损耗的影响，直流偏磁下的铁心损耗大于无偏磁下的铁心损耗。文献[9]分析了高频变压器的铁损耗精确测量方法。文献[10]仿真分析了磁通分布和铁损耗的关系，可指导变压器铁心的设计。文献[11,12]分别分析了铁心损耗在不同频率激励下的铁损耗变化规律。文献[13-15]分析得出了变压器铁心饱和是励磁涌流产生的主要原因。采用低频法测量电力系统中铁磁元件的铁心损耗，能大大减小实验电源容量，降低实验成本，因此具有较大的工程实用价值。

本文采用低频电源进行铁磁元件空载实验。测量低频下的铁心损耗，再根据相关算法折算至工频实验条件下，达到采用低频实验代替工频实验的目的。由于铁磁元件铁心饱和时的电压基本与电源频率呈正比，在低频电源的激励下，能够成倍降低电源电压，而电流基本相等，从而减小实验电源的容量。

1 基本原理

本文采用几个低频率的正弦波电源来测量电力系统中铁磁元件低频下的涡流损耗和磁滞损耗，并根据相应折算算法得到折算至工频实验下的铁心损耗。

1.1 铁磁元件等效电路

铁磁元件一侧开路的等效电路如图1所示。图1中，Rdc为绕组上的直流电阻，Lσ为该侧绕组漏感，Re为涡流损耗等效电阻，带磁滞回环的非线性电感Lm为励磁电感[16]，Lm中包含磁滞损耗Ph，iex(t)为励磁电流，im(t)为流过Lm的磁化电流，ie(t)为涡流损耗等效电流，e(t)为感应电动势，u(t)为施加在绕组上的励磁电压。

图1 铁磁元件等效电路Fig.1 Equivalent circuit of ferromagnetic components

由式(1)、式(2)[17]可知，当饱和程度(磁通Φ)相同时，磁化电流Im不变，而感应电动势有效值E与频率呈正比，空载时的漏感和直阻上的压降很小，励磁电压U几乎与电动势E相等，因此励磁电压U几乎与频率呈正比。涡流电流Ie随频率减小，但Ie通常比Im小很多，从式(3)可得，励磁电流Iex稍减小。由式(4)可知，实验电源容量Spower基本与频率f呈正比。因此随着频率降低，实验电源容量大大减小。

E=4.44fNΦ

(1)

(2)

Iex=Ie+Im

(3)

Spower=UIex≈4.44fNΦIex

(4)

式中，S为铁心横截面积；H为磁场强度；l为磁路长度；N为铁心匝数；μ为铁心材料的磁导率。

1.2 铁心损耗的组成

变压器损耗是指在额定电压下空载运行时变压器铁心所消耗的能量，其包括铁心损耗PFe和空载电流在绕组中产生的铜耗PCu。而铁心损耗又可分为磁滞损耗Ph、涡流损耗Pe和附加损耗。通常绕组铜耗和附件损耗都只占变压器损耗的很小一部分，可忽略。因此本文主要分析磁滞损耗和涡流损耗。

大量实验分析表明，磁滞损耗Ph的计算式为[17]

(5)

式中，Ch为磁滞损耗系数，其大小决定于材料的性质，与频率无关；对一般硅钢片，可取指数n=1.6～2.3；Bm为铁心磁感应强度最大值；V为铁心体积。

涡流损耗的计算式为[17]

(6)

式中，f为频率；Ce为涡流损耗系数，其大小取决于材料的电阻率，与频率无关；Δ为硅钢片厚度[13]。

铁心中磁滞损耗和涡流损耗之和为铁心损耗，通常可用Steinmetz公式即式(3)进行计算。对于同一个铁磁元件，其铁心体积V、硅钢片厚度Δ、磁滞损耗系数Ch、磁滞损耗系数Ce都是定值。因此如果保证不同频率下的Bm一致，则可以认为We、Wh为常数。

=Whf+Wef2

(7)

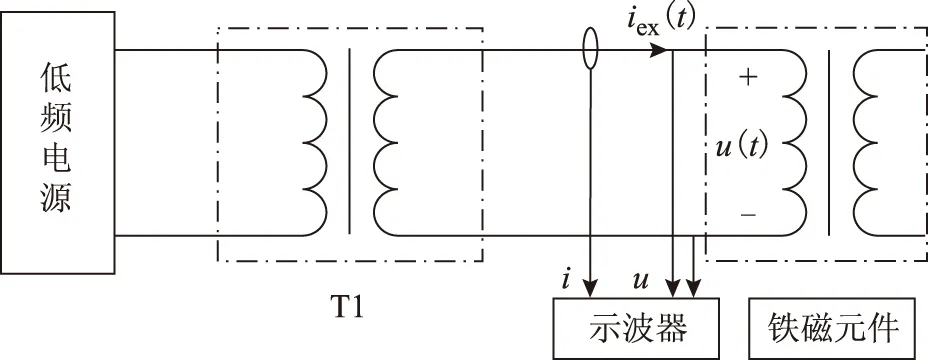
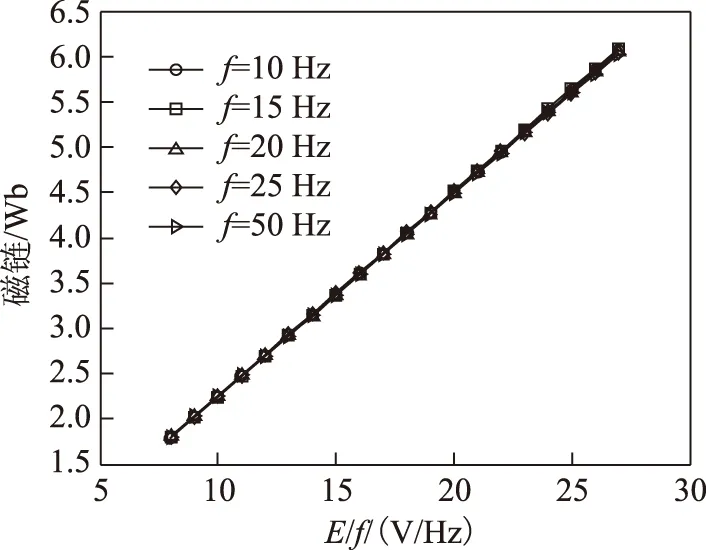
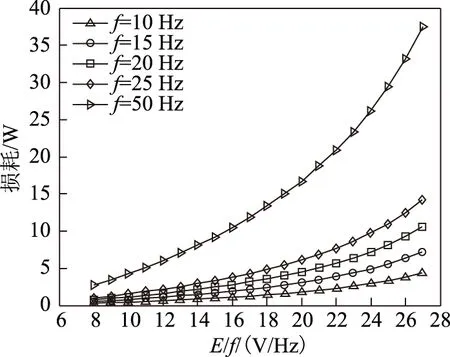
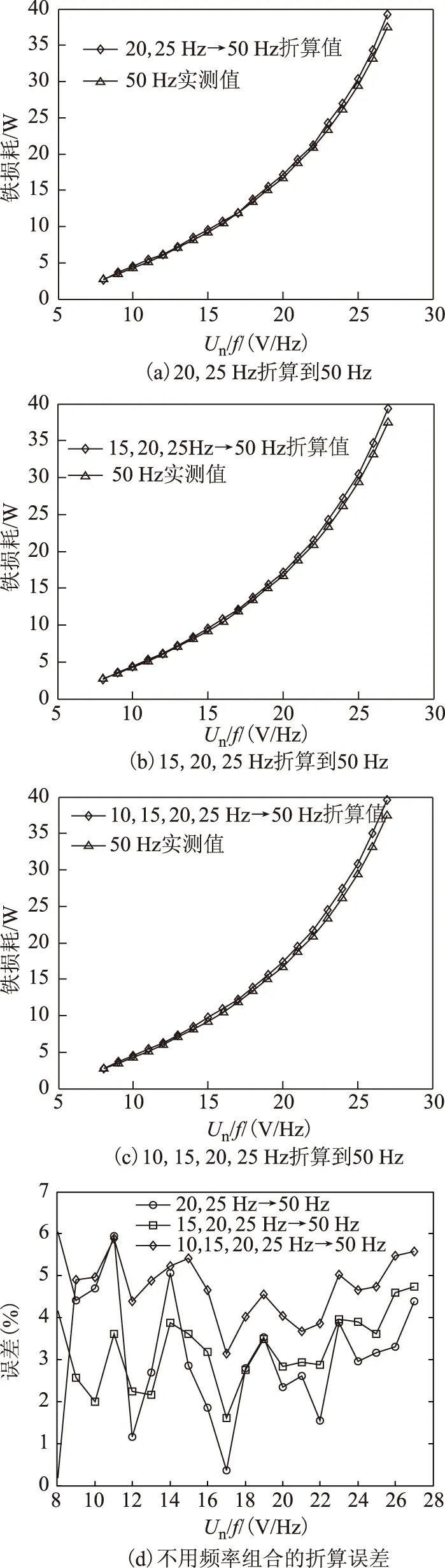
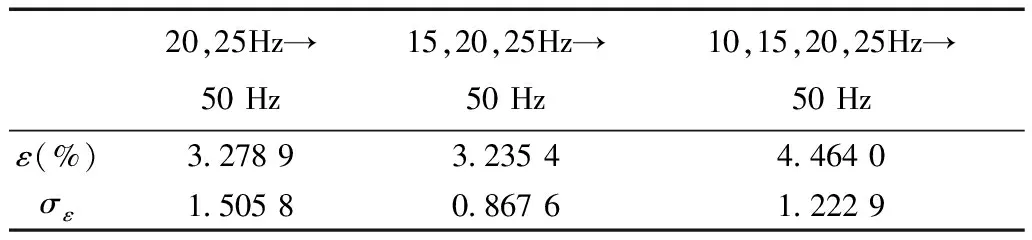
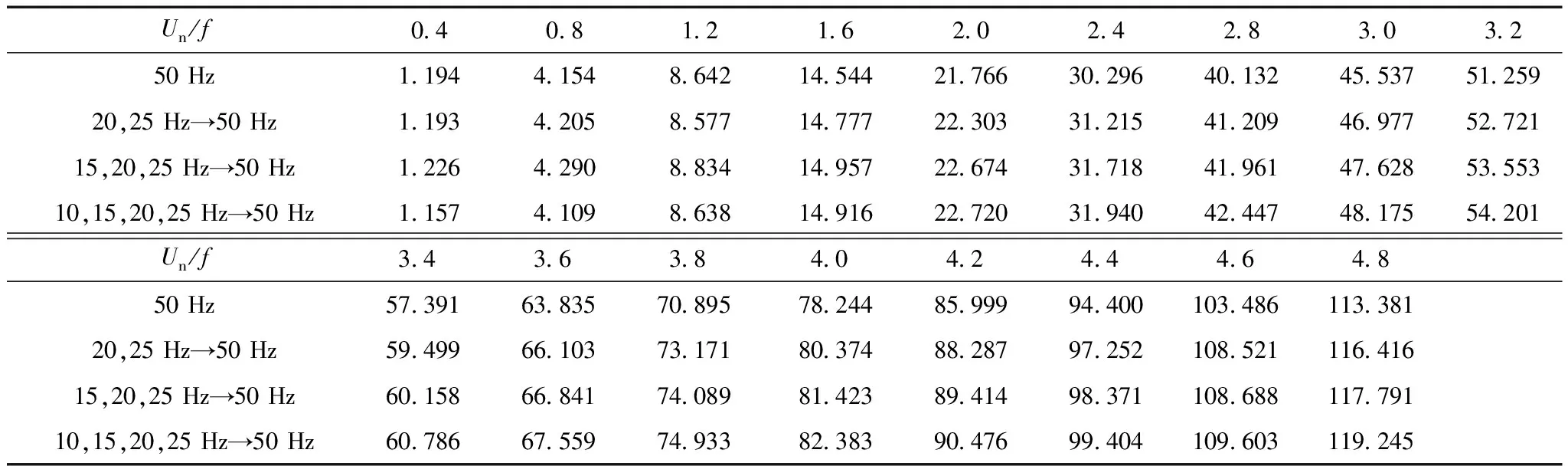
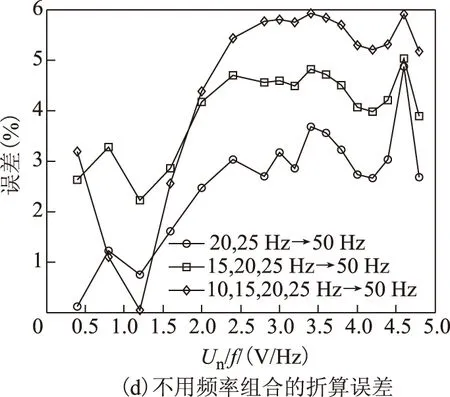
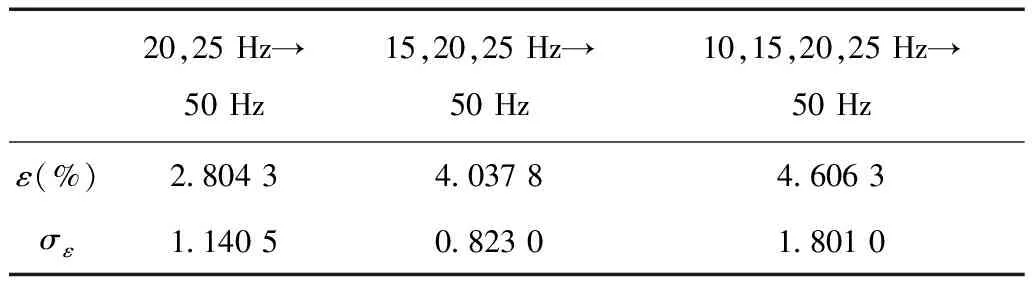
式中，Wh、We分别为每个磁化周期产生的单位磁滞损耗(W/Hz)和涡流损耗(W/Hz2)； 1 Hz

保持不同频率下的磁通幅值相等，可通过两个不同频率下的铁心损耗求出Wh和We，再代入工频fn=50 Hz即可求得工频下的铁心损耗。由E=KvfNBmS(正弦波时Kv=4.44)[20]、Ψ=NBmS知，可通过计算铁心磁链Ψ是否相等来判断磁感应强度是否相等。

感应电动势计算式为

(8)

磁链计算式为

(9)

式中,T为感应电动势周期。

1.2 低频法铁心损耗的计算

考虑到采用两个频率计算的We和Wh可能具有一定的偶然性，为了使计算结果更加精确，本文采用多组频率下的实验数据来计算We和Wh。绕组一侧开路，一侧施加电压，记录电压、电流数据。

铁损耗的计算式为

(10)

计算各个频率下对应的铁损耗，PFem为第m个频率下的铁损耗，得到

(11)

将式(7)写成矩阵形式为

FX=P

(12)

其中

式中，F为频率矩阵；X为被求参数We、Wh组成的矩阵；P为铁损耗矩阵。对于式(7)，采用最小二乘法可求得We和Wh。

X=(FTF)-1FTP

(13)

因此，折算到工频下的铁损耗为

(14)

式中，fn为额定频率，一般为50Hz或60Hz。

铁损耗电流可分为磁滞损耗电流与涡流损耗电流，即

(15)

式中，IFe、Ih、Ie分别为铁损耗、磁带损耗、涡流损耗对应电流的有效值。

由E=KvfNBmS可知，E与频率f呈正比，因此涡流损耗电流ie与频率呈正比，磁滞损耗电流ih与频率无关。而不同频率下Bm相等，所以im相等，折算到工频下的励磁电流为

(16)

折算到工频下的励磁电压为

(17)

这样便可得到折算到工频的励磁电压Un与工频损耗PFen的对应关系。值得提出的是本文方法的频率适用范围为1～60Hz。

2 实验装置及方法

2.1 实验装置

实验装置示意图如图2所示。其中，低频电源采用PCR2000LE，用来产生频率可变(0.1～999.9Hz)的正弦波；变压器T1起升降压的作用(电压比可调，额定最高输出电压3.5kV)，同时还可以起到隔离直流的作用，消除直流偏磁的影响；示波器(力科HDO8000)记录绕组两端电压、电流数据(电压探头：HVD3106，电流探头：CP030A)；试品为变压器、互感器等铁磁元件。

图2 实验装置示意图Fig.2 Testing apparatus diagran

2.2 实验方法与过程

为了验证本文低频折算法的准确性，选取型号为LMZ-3电流互感器和一台配网动态模拟实验室的单相变压器为实验对象。互感器参数：电流比为1 000A/1A，额定电压为3kV，直流电阻Rdc1=4.902Ω(直阻仪测得)；变压器参数：电压比为380V/220V，额定容量为16.7kV·A，空载电流<1.5%，空载损耗<1.2%，阻抗电压14%。低压侧直流电阻Rdc2=0.018 07Ω(直阻仪测得)，根据名牌参数和直阻计算得到低压侧漏感Lσ=6.432×10-4H。

按照图2所示接线，变压器从低压侧加压，高压侧绕组开路;互感器从二次侧加压，一次侧开路。分别施加四个频率(10Hz、15Hz、20Hz、25Hz)的正弦波进行铁磁元件空载实验。由于实验过程中E无法实时测量，因此实验时保证不同频率下U/f相同，记录电压、电流数据，再根据式(8)、式(10)计算得到不同频率下的E/f-PFe曲线，采用三次样条插值计算不同频率、相同E/f下的铁心损耗，最后根据式(10)～式(17)折算至工频50Hz下铁损耗PFen和励磁电压Un。分析采用低频折算法的计算结果和50Hz实测结果的误差。

3 实验结果与分析

3.1 互感器实验结果

设置示波器采样点数为50 000，采集测试过程中的电压、电流数据，采用Matlab对实验数据进行分析。互感器(CurrentTransformer,CT)的漏感Lσ很小，计算时可忽略。

为了分析不同频率下的Bm是否相等，按照式(8)、式(9)计算不同频率下E/f相同时的磁链，结果如图3所示。可看出当E/f相等时，磁链基本相等。

互感器在频率不同、E/f值相同时的铁心损耗如图4所示，可看出频率减小1/2，损耗约减小到1/3。

图3 互感器频率不同、E/f相等时的磁链Fig.3 The flux linkage of CT at different frequency under constant value of E/f

图4 互感器频率不同、E/f相等时的铁心损耗Fig.4 Core loss of CT at different frequency and constant value of E/f

图4 互感器频率不同、E/f相等时的铁心损耗Fig.4 Core loss of CT at different frequency and constant value of E/f

由于数据量较多，受篇幅限制，本文中没有给出不同频率下、不同电压下铁心损耗的实验数据。

采用三次样条插值法分别计算互感器在不同频率、相同E/f下的铁心损耗，并采用式(10)～式(17)计算推算至工频50Hz下的损耗，得到Un/f-PFe曲线。比较Un/f相同时的折算值和工频50Hz实测损耗，分析其测量误差。表1为互感器不同频率组合的折算结果与50Hz实测铁心损耗的实验数据对比。

表1 互感器低频法和工频法的铁心损耗实验数据对比

图5为互感器在不同频率组合的折算值与工频50 Hz 实测结果的比较。可看出采用本文所述的低频折算法折算值与工频实测值有很好的吻合度。

图5 互感器不同频率组合的折算值与50 Hz实测值对比Fig.5 Comparison of test results at 50 Hz and conversion results of current transformer at different frequency combination

从图5d可看出，几种频率组合下采用15,20,25 Hz 折算到50 Hz的折算相对误差最小，每个点的相对误差ε均不超过5%。几种折算方法的折算相对误差与误差标准差σε见表2，由此可见采用三个频率(15,20,25 Hz)折算到50 Hz的折算相对误差平均值和标准差都更小，因此折算效果最好。

表2 互感器不同频率组合折算误差

3.2 变压器实验结果

互感器的漏感很小，基本可忽略，简化了图1中的等效电路。但是对于电压等级高、容量大的变压器而言，漏感相对较大，在电流较大时，漏感上的压降不能忽略，因此采用式(8)计算变压器的感应电动势时，需要考虑变压器漏感的压降。认为漏感为空心电感，不产生有功损耗，且与频率无关，因此式(10)对于变压器同样适用。本文在变压器上展开实验，分析该方法的折算效果。

变压器在不同频率、相同E/f值下的铁心损耗如图6所示，50 Hz下电压最高加到约1.1Un(240 V)，变压器出厂实验值一般为1.1Un[2]。

图6 变压器频率不同、E/f相等时的铁心损耗Fig.6 Core loss of transformer at different frequency and constant value of E/f

同理，采用三次样条插值法分别计算变压器在不频率、相同E/f时的铁心损耗，计算推算至工频50Hz下的损耗，得到Un/f-PFe曲线。比较Un/f相同时折算值和工频50 Hz实测损耗，分析其测量误差。

表3为变压器不同频率组合的折算结果与50 Hz铁心损耗的实验数据。图7为变压器不同频率组合的折算值与工频50 Hz实测结果的比较。从图7可看出，变压器采用本文算法与工频实测值仍有很好的吻合度，验证了本文方法的正确性。从图7d可看出，几种频率组合下采用20,25 Hz和15,20,25 Hz折算到50 Hz 时，每个点的折算相对误差ε仍均不超过5%。几种折算方法的折算相对误差与相对误差标准差σε见表4，虽然采用20,25 Hz的相对误差平均值较小，但是其标准差比采用15,20,25 Hz大，稳定性比采用三个频率组合时差。

表3 变压器低频法和工频法的铁心损耗对比

图7 变压器不同频率组合的折算结果与50 Hz实测值对比Fig.7 Coparison of test results at 50 Hz and conversion results of transformer at different frequency combination

20，25Hz→50Hz15，20，25Hz→50Hz10，15，20，25Hz→50Hzε(%)2 80434 03784 6063σε1 14050 82301 8010

图8为变压器采用不同频率所需的实验电源容量和工频实验所需的实验电源容量的比较，纵坐标为工频实验电源容量Spowern与低频电源容量Spower的比值。可以看出所需实验电源容量的大小与频率基本呈正比，曲线出现峰值的原因可能是低频下的励磁电流变化较快，使低频下的实验电源容量变化较快，而且频率越低，Spowern/Spower变化越明显，因此10 Hz时峰值现象最明显。

图8 不同频率下的实验电源容量Fig.8 The capacity of power supply under different frequency

4 结论

通过采用几个频率的低频正弦波对铁磁元件进行空载实验，计算低频下的铁损耗，采用三次样条插值计算不同频率下E/f相等时的铁损耗，采用本文提出的基于最小二乘原理的折算算法推算工频50 Hz下的铁损耗，并与工频实测铁损耗进行比较，可得到以下结论：

1)本文分别采用两个频率、三个频率和四个频率折算，综合互感器和变压器实验结果，采用三个频率折算的相对误差和相对误差标准差较小，稳定性较好，实际工程应用中建议采用三个频率折算。

2)采用低频法测量铁磁元件铁心损耗，可大大减小实验电源容量。所需的实验电源容量基本与频率呈正比，缺点是要多次测量，但是如果后期能研制出自动化测量、分析设备，可极大地减少实验成本和时间。

3)本文采用15,20,25 Hz三个频率下的损耗计算工频下的损耗与工频实测损耗的相对误差ε<5%，折算相对误差标准差σε<0.9，具有较好的折算效果，后期可以考虑添加修正系数的方法修正不同频率下的折算误差，使测量精度更高。

[1] GB1094.1—2013,电力变压器 第一部分: 总则[S].2013.

[2] JB/T 501—2006,电力变压器试验验导则[S]. 2006.

[3] 梁仕斌, 文华, 赵涓, 等. 低频变频电源测量铁磁元件伏安特性的一种补偿计算方法[J]. 中国电机工程学报, 2010, 30(3): 125-129. Liang Shibin, Wen Hua, Zhao Juan, et al. A compensation calculation method for measuring ferromagnetic component volt-ampere characteristic using low frequency and frequency conversion power[J]. Proceedings of the CSEE, 2010, 30(3): 125-129.

[4] 张艳丽, 刘洋, 谢德馨, 等. 一种考虑硅钢片旋转损耗的三相变压器铁心损耗简化计算方法[J]. 中国电机工程学报, 2013, 33(18): 126-131. Zhang Yanli, Liu Yang, Xie Dexin, et al. A simplified calculation method of core losses considering rotating losses of electrical steel sheets in three-phase transformers[J].Proceedings of the CSEE, 2013, 33(18): 126-131.

[5] 张艳丽, 彭志华, 谢德馨, 等. 直流偏磁下不同磁化曲线对变压器铁心损耗仿真的影响[J]. 电工技术学报, 2014, 29(5): 43-48. Zhang Yanli, Peng Zhihua, Xie Dexin, et al. Effect of different magnetization curves on simulation for transformer core loss under DC bias[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 43-48.

[6] 赵小军, 崔灿, 李琳, 等. 基于定点谐波平衡法的铁心磁滞与损耗特性分析[J]. 电工技术学报，2014, 24(5): 46-51. Zhao Xiaojun, Cui Can, Li Lin, et al. Analysis of the hysteresis and loss characteristic in the laminated core by fixed-point harmonic-balanced method[J].Transactions of China Electrotechnical Society, 2014, 24(9): 46-51.

[7] 赵小军, 李琳, 程志光, 等. 定点谐波平衡有限元法与叠片铁心直流偏磁磁化特性研究[J]. 中国电机工程学报, 2011, 31(9): 126-132. Zhao Xiaojun, Li Lin, Cheng Zhiguang, et al. Fixed point harmonic-balanced finite element method and DC-biasing magnetizing characteristic of laminated core[J]. Proceedings of the CSEE, 2011, 31(9): 126-132.

[8] 郭满生, 梅桂华, 张喜乐, 等. 直流偏磁条件下单相三柱电力变压器损耗计算[J]. 电工技术学报, 2010, 25(7): 67-71. Guo Mansheng, Mei Guihua, Zhang Xile, et al.Calculation of losses in single phase three limb transformer under DC-biasing[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 67-71.

[9] Mu Mingka, Li Qian, David J G, et al. New core loss measurement method for high-frequency magnetic materials[J].IEEE Transactions on Power Electronics , 2014, 29(8): 4374-4381.

[10]Tenyenhuis E G, Mechler G F, Girgis R S. Flux distribution and core loss calculation for single phase and five limb three phase transformer core designs[J]. IEEE Transactions on Power Delivery, 2000, 15(1): 204-209.

[11]Ibrahim M, Pillay P.Advanced testing and modeling of magnetic materials including a new method of core loss separation for electrical machines[J]. IEEE Transactions on Industry Applications, 2012, 48(5): 1507-1515.

[12]Hasan S, Taib S, Hardi S, et al. Core loss characteristics analysis of power transformer under different frequencies excitation[C]//7th International Power Engineering and Optimization Conference, Langkawi, 2013: 619-623.

[13]何小庆, 刘淑萍, 李攀宏, 等. 一种消除单相变压器励磁涌流的预充磁策略[J]. 电力系统保护与控制, 2014, 42(17): 120-124. He Xiaoqing, Liu Shuping, Li Panhong, et al. Eliminating the single-phase transformer inrush current based on pre-magnetizing[J]. Power System Protection and Control, 2014, 42(17): 120-124.

[14]傅伟, 赵莉华, 梁勇, 等. 多台变压器空载合闸励磁涌流及其抑制方案的研究[J]. 电力系统保护与控制, 2015, 43(1): 28-33. Fu Wei, Zhao Lihua, Liang Yong, et al. Study on no-load closing inrush current of transformer group and suppression measures[J]. Power System Protection and Control, 2015, 43(1): 28-33.

[15]姚东晓, 邓茂军, 倪传坤, 等. 变压器多侧励磁涌流产生机理及对差动快速动作区影响研究[J]. 电力系统保护与控制, 2016, 44(5): 36-41. Yao Dongxiao, Deng Maojun, Ni Chuankun, et al. Transformer′s multi-side inrush current generation mechanism and its influence on the differential protection′s fast action zone[J]. Power System Protection and Control, 2016, 44(5): 36-41.

[16]León F D, Farazmand A, Jazebi S, et al. Elimination of residual flux in transformers by the application of an alternating polarity DC voltage source[J]. IEEE Transactions on Power Delivery, 2015, 30(4): 1727-1734.

[17]汤蕴璆.电机学[M]. 北京: 机械工业出版社, 2011.

[18]Steinmetz C P. On the law of hysteresis[J]. Proceedings of the IEEE, 1984, 72(2): 196-221.

[19]Bertotti G. General properties of power losses in soft ferromagnetic materials[J]. IEEE Transactions on Magnetics, 1988, 24(1): 621-630.

[20]朱春波, 徐德鸿, 张龙龙, 等. 应用于电力电子技术的变压器和电感——理论、设计与应用[M]. 北京:机械工业出版社, 2014.

(编辑 张洪霞)

Core Loss Measurement of the Ferromagnetic Components Using Low-Frequency Method Frequency Power Supply

LiuXin1YaoChenguo1LiangShibin2WangJunkai1LiuTao3

(1.State Key Laboratory of Power Transmission Equipment & System Security and New Technology Chongqing University Chongqing 400044 China 2.Yunnan Electric Power Test & Research Institute (Group) Co.Ltd Kunming 650051 China 3.Yunnan Electric Power Technology Company Kunming 650051 China)

Transformers will have measured no-load excitation characteristics, no-load loss and load loss for factory tests. Generally, a large capacity of industrial-frequency (IF) power supply is needed to measure the no-load loss which mainly consists of core loss. In order to reduce the capacity of testing power supply and make the test equipment portable, a low-frequency power supply rather than IF power supply which was used for core loss measurement of ferromagnetic components, was demonstrated in this paper. By applying several low frequencies voltages, the cure ofE/f-PFe(electromotive force/frequency-core loss) via calculating core loss under low-frequency can be first obtained. Core loss under low-frequency of different frequency at constant value ofE/fwere then calculated through spline interpolation method. Lastly, the converted core loss under IF was determined based on least square method. In addition, experiments were conducted on the current transformer (CT) and single phase power transformer, comparing conversion results which using 15,20,25 Hz with directly measured results under IF, the relative errorεis below 5% and standard deviation of relative errorσεis less than 0.9, respectively. These results show that this method possesses high conversion accuracy and stability and reduces the capacity of testing power supply obviously.

Ferromagnetic components, core loss, low-frequency method, least squares method, eddy loss

中国南方电网有限责任公司科技项目资助(K-YN2014-136)。

2016-04-06 改稿日期2016-05-28

TM416

刘 鑫 男，1992年生，硕士研究生，研究方向为互感器、变压器等设备检测方法。

E-mail：alxenderking@cqu.edu.cn(通信作者)

姚陈果 男，1975年生，教授，博士生导师，研究方向为变压器在线监测技术和脉冲功率技术在生物医学中的应用。

E-mail：yaochenguo@cqu.edu.cn