电工软磁材料旋转磁滞损耗测量及建模

张长庚 杨庆新,2 李永建

(1. 河北工业大学电磁场与电气可靠性省部共建重点实验室 天津 300130 2.天津工业大学电工电能新技术天津市重点实验室 天津 300387)



电工软磁材料旋转磁滞损耗测量及建模

张长庚1杨庆新1,2李永建1

(1. 河北工业大学电磁场与电气可靠性省部共建重点实验室 天津 300130 2.天津工业大学电工电能新技术天津市重点实验室 天津 300387)

电力变压器和电机中存在旋转铁心损耗是其损耗预测不准的主要原因之一。针对该问题，提出电工软磁材料旋转磁滞损耗测量及建模方法。首先，矢量磁滞损耗分解为切向损耗和法向损耗两部分，分别根据圆形旋转损耗和交变损耗建模。其次，对软磁复合材料和无取向电工钢片进行模型参数辨识，并比较两种材料的损耗特性和模型参数。最后，利用三维磁特性测量装置进行多种励磁模式下的损耗测量，并对比实验结果与模型预测值。结果表明，在旋转复杂激励下，所提出的模型比传统的Steinmetz模型有更高的精度。

电机铁耗 磁滞损耗 电磁场数值模拟 旋转损耗

0 引言

高效率的电机和电力变压器的使用能够节约社会总能源消耗，是响应国家节能减排发展战略的有效措施。设计高效率的电机和电力变压器，一方面改进或提出新的结构、工艺和控制策略，例如三维磁通电机；另一方面减少磁性材料本身的铁耗，例如采用新型非晶纳米晶材料[1]。两方面都依赖准确的铁心材料的磁特性测量和建模。早在电机等电磁装置用于工业生产之初，1892年S.Steinmetz提出了著名的磁滞损耗计算Steinmetz公式[2]。该公式适用于正弦稳态下的损耗预测，随着HVDC和电力电子设备的广泛应用，大量谐波引入电机和变压器设备，为解决复杂磁通密度波形的激励，提出了多种修正的Steinmetz公式。文献[3] 引入等价频率的概念，考虑非正弦磁通密度励磁下的损耗改进Steinmetz公式。文献[4]提出广义的Steinmetz公式，进一步考虑小磁滞回环对损耗的贡献。文献[5]考虑频率和磁通密度对Steinmetz公式系数的影响，通过拟合变系数的公式，提高损耗计算精度。文献[6]考虑电力变压器的杂散损耗和屏蔽钢板的铁耗。为了获得更高精度磁滞损耗的估计，各种经典标量磁滞模型，如Preisach模型、Play模型和Jiles-Atherton(JA)模型等相继被提出。

在电力变压器和电机实际运行中发现旋转磁场激励下损耗大于单方向的交变损耗。对旋转损耗的研究分为两类：①基于Steinmetz公式方法和矢量磁滞模型方法，文献[7]在频域空间把二维空间磁通密度B轨迹分解为圆形旋转磁通密度和交变磁通密度两部分，根据交变损耗系数和旋转损耗系数分别利用Steinmetz公式进行损耗估计；②建立矢量的磁滞模型，如新型混合矢量磁滞模型。文献[8]利用Stoner-Wohlfarth模型求解磁滞算子矢量磁化强度方向，再利用Preisach模型矢量加和所有单个磁滞算子的磁化强度。因而，准确的磁滞模型和损耗模型有助于从铁心磁化本质上理解变压器的磁化和损耗特性，解决相应的工程问题如励磁涌流问题[9,10]。基于磁滞模型的损耗计算方法，通过有限元方法耦合标量或矢量磁滞模型，解法器迭代次数多，算法复杂计算量大[11,12]；基于Steinmetz公式类交变损耗和旋转损耗方法，计算过程简单但精度较低[13]，广泛用于电机本体设计和效率分析[14]。传统Steinmetz公式是稳态计算方法，为了避免电磁有限元计算存储每一步的计算结果，文献[15] 提出瞬态的Steinmetz计算方法，有效减少了计算量。

无论是材料的精确磁滞模型还是Steinmetz公式的经验模型，模型应用的前提是参数的辨识，首先获得模型所需要的材料磁特性测量数据。可靠的材料模型数据获得依赖准确的可重复的磁特性实验测量。电工钢片一维国家测量标准是爱泼斯坦方圈方法；国际上一些科研团队研制了不同结构形式的二维单片磁特性测量系统，根据励磁结构和磁化样品的不同，可分为水平形式方形样片旋转测量仪[16]、水平圆形样片旋转测量仪[17]、垂直型旋转测量仪等[18]。悉尼科技大学针对软磁复合材料研发了首个三维软磁材料磁特性测量仪[19]。国内沈阳工业大学对硅钢片软磁材料进行了二维磁特性测量[20]。河北工业大学研制了宽频(20～1 000Hz)大功率软磁材料的三维磁特性测量装置[21]。

本文提出一种基于旋转磁特性测量的瞬态矢量磁滞损耗模型。该模型统一描述了交变磁滞损耗和旋转磁滞损耗，能够预测对空间任意磁通密度轨迹的瞬时磁滞铁耗。其基本原理是将空间磁通密度轨迹的运动分解为切向运动和法向运动，其中法向磁通密度轨迹运动采用交变损耗计算，切向磁通密度运动采用旋转损耗计算方法。利用三维磁特性测量装置对无取向硅钢片进行交变损耗、旋转损耗和变轴比的椭圆激励的磁滞损耗测量。根据本文提出的矢量磁滞损耗模型，预测了变轴比的复合型椭圆激励下的磁滞损耗，验证了该模型的有效性。

1 旋转损耗模型的定义

1.1 改进矢量磁滞模型的定义

本文基于传统的矢量Play磁滞模型[12]提出考虑旋转磁化的改进型矢量磁滞模型。传统的矢量Play模型依赖于圆形磁滞算子Hk(H)的叠加运算，即

(1)

式中，B为磁通密度；H为磁场强度；n为磁滞算子的数量；fk为非线性的映射函数从磁场强度空间映射到磁通密度矢量空间；Hk(H)为圆形的Play磁滞算子。磁场强度超前的空间距离即为磁滞算子半径。

图1为软磁材料椭圆磁化轨迹和改进磁滞模型，图中椭圆表示磁滞算子，椭圆形磁滞算子的边界到算子中心的空间距离表示磁场强度的空间超前矢量，磁滞算子随磁化轨迹的运动而运动。磁滞算子椭圆长轴和短轴在不同空间位置的长度表征磁性材料磁特性，根据二维或三维矢量磁特性测量建模和辨识。椭圆圆心表示无磁滞磁场强度Hnon，椭圆形算子的长轴或短轴之一位于椭圆圆心与坐标原点的连接线上。算子的圆心位于磁化轨迹的圆弧上，表示无磁滞的磁场强度轨迹。磁场强度轨迹逆时针旋转，相应磁通密度轨迹也逆时针旋转，两者关系由磁场饱和、磁场各向异性和磁滞等因素决定。dB/dt的射线代表磁通密度矢量的空间变化方向，一维dB/dt表示磁通密度的增加或减少，从而决定磁场强度超前于磁通密度的方向。

图1 软磁材料椭圆磁化轨迹和改进磁滞模型Fig.1 The elliptic magnetization locus of soft magnetic material and the improved hysteresis model

宏观磁场强度Hhys分解为两部分，即

Hhys=Hnon+Hcr

(2)

式中，Hcr为矫顽磁场强度；Hnon仅为磁通密度B的函数。Hcr是在椭圆中心点处作斜率为dB/dt的射线与磁滞算子的相交线段。当交变励磁时，dB/dt的射线沿轨迹的轴线方向；当圆形励磁时，射线沿圆形轨迹的切向方向；当椭圆形励磁时，射线位于两者之间。Hnon计算式为

Hnon=g(B)

(3)

对于各向同性材料，矢量Hnon方向与B方向相同，函数g的幅值可选为正切函数或Langevin函数；对于各向异性软磁材料函数，g是空间二维矢量函数。综上，矢量磁滞模型的计算流程如图2所示。

图2 改进磁滞模型计算流程Fig.2 Control flow chart of improved hysteresis model

本文提出的改进矢量磁滞模型与传统的矢量Play模型区别如下：

1)矢量Play模型以磁场强度H为变量，而改进模型以B为变量，因此后者也被称为磁滞逆模型。当进行基于磁矢位A的有限元分析时，逆磁滞模型避免迭代运算，提高了计算效率。

2)传统矢量Play模型磁滞算子为圆形，改进模型磁滞算子为椭圆形且考虑了旋转磁化过程。

3)两种模型中的非线性映射函数是一对互逆的函数。

1.2 矢量磁滞损耗分解

软磁材料的比损耗，即单位时间内的磁场做功，计算式为

(4)

Hnon磁场分量瞬时吸收或释放能量，但一个周期内做功的积分为零。磁通密度增加时储存静磁能，磁通密度减小时释放静磁能，本质上不消耗能量，从而使磁性器件外特性为感性。磁滞能量的耗散仅来自于矫顽磁场Hcr部分，如图1所示，矫顽磁场部分依赖椭圆形磁滞算子进行插值计算，Hcr总是超前于无磁滞的磁场强度Hnon。商用软件如Ansys-Maxwell中，矫顽磁场强度沿直角坐标系正交分解为两部分，即

Hcr=Hxcrix+Hycriy

(5)

式中，Hxcr、Hycr分别是x、y方向的矫顽力。则总磁滞损耗相应分解为两部分之和，即

(6)

直角坐标系下的正交分解不能有效表征旋转磁滞损耗的物理过程。旋转磁化的铁磁学机理是磁畴壁的旋转，而在低场强的交变磁化时本质是磁畴壁的移动。实验发现接近饱和时的旋转磁滞损耗接近于零，因此理论上矫顽磁场强度也应该为零。式(5)中，Hxcr、Hycr独立采用交变矫顽力建模方法，故式(6)计算的两个方向独立的交变损耗之和大于旋转磁化损耗，这与实验结果不符。

为了解决该问题，本文将矫顽磁场强度分解为法向和切向两部分。椭圆的两个轴分别是切向轴和法向轴，法向轴与坐标原点和椭圆中心连线重合，切向轴与连线垂直。沿法向轴分解的磁损耗受交变磁化影响，沿切向轴分解的磁损耗受旋转磁化影响，则

(7)

1.3 幅值交变磁滞损耗建模

幅值矫顽磁场强度的建模，根据等价的椭圆模型，假设励磁波形是标准正弦，矫顽磁场强度符合余弦规律变化，则

(8)

式中，Bm为磁化历史记录的最大磁通密度；Hm为最大的矫顽力；ω为时变磁场的角频率。联立式(4)和式(8)，幅值交表磁滞损耗简化为

(9)

式中，f为励磁频率。根据Berotti损耗分离定律交变磁滞损耗假设得

(10)

式中，kh为磁滞损耗系数。式(7)与式(6)联立解得

(11)

故瞬时交变磁滞损耗计算式为

(12)

式中，Br为矢量B在椭圆轨迹法向方向的分量，当交变磁化时Br为矢量B的幅值。

1.4 旋转磁滞损耗建模

图3为软磁材料圆形旋转磁化过程磁场强度，磁通密度幅值Br不变，B滞后于H空间角度θ，且θ是圆形旋转磁通密度幅值Br的函数。当磁性材料的磁化轨迹为圆形时，瞬时功率式(4)简化为

(13)

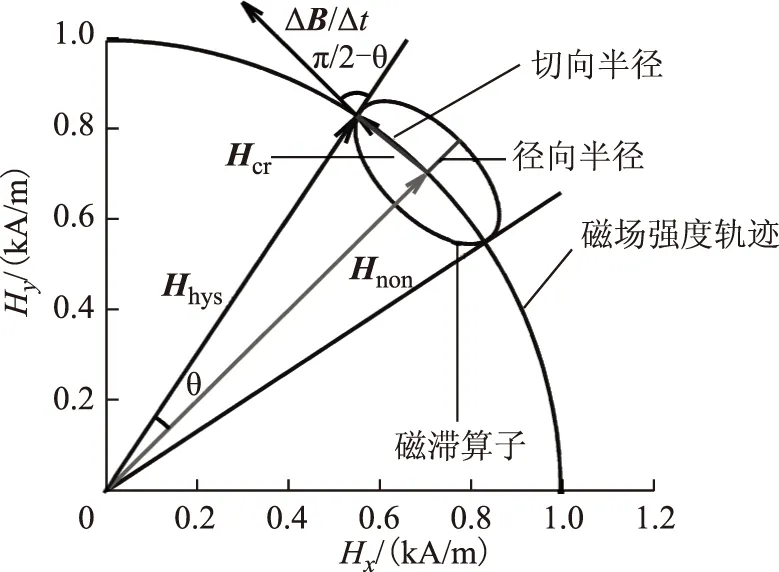
图3 软磁材料圆形旋转磁化过程磁场强度Fig.3 Soft magnetic material magnetic field intensity of rotational magnetization process

(14)

在有限元计算中，Hnon可以通过磁通密度非线性关系直接计算，H通过磁滞模型计算，故切向计算式更实用。由于磁性材料SMC和无取向钢片都存在一定的空间各向异性，当磁通密度轨迹运动时，空间角度差θ不恒定。为了进一步简化损耗模型，取空间角度差的积分平均值作为损耗模型的特征参数，即

(15)

式中，α为磁通密度矢量的空间角度。

(16)

式中，B1为基波幅值。由于磁性材料的非线性，磁场强度H产生高次谐波的畸变为

(17)

式中，Hi为各奇次谐波幅值；θi为各次谐波相位。单位时间平均功率的积分表达式为

(18)

式中，θ1为Hx的基波分量与Bx基波的相位差。式(18) 说明对于圆形磁通密度的励磁模型，旋转损耗仅决定于基频下的相角差θ1，Hx、Hy的高次谐波部分对磁滞损耗无贡献。此时H1仅是H基波的幅值，故在式(12)增加修正系数，即

(19)

当样品未达到饱和时，系数k≈1； 当样品过饱和时，系数k略小于1。进一步给出损耗模型旋转部分的计算式为

(20)

综上，通过式(12)和式(20)分别计算幅值交变损耗和切向瞬时旋转损耗。文献[7]中旋转损耗的分解算法是在频域下，需要有限元后处理存储每一时刻每一网格位置的磁场。本文提出的算法在时域进行磁通密度轨迹的分解，显著节约内存，降低计算量。

2 损耗模型辨识方法

根据本文提出的旋转损耗模型对软磁复合材料SMC-Somaloy500和无取向硅钢片35WW270进行模型参数的辨识和数值实现。

2.1 交变损耗模型参数辨识

无论采用哪种动态磁特性测量方法，在交变或旋转激励下，磁性材料测量总铁耗不仅包含磁滞损耗Ph而且含有经典涡流损耗Pc和异常损耗Pe。随着励磁频率的升高，涡流损耗和异常损耗在总损耗的占比增加起主导作用。仅在极低测量频率(1Hz)时，可忽略剩余两部分，认为测量损耗仅是磁滞损耗。常用的实验损耗分离和处理方法是根据经典的Steinmetz公式理论，将磁性材料总损耗Pv进行理论分解，即

(21)

式中，kh、kc、ke分别为交变磁滞损耗系数、涡流损耗系数和异常损耗系数。

通过测量多个频率的Bm-P损耗曲线，拟合模型损耗参数，求解最优化问题，即

(22)

优化问题采用基因算法求解。对于无取向硅钢片的优化拟合,采用20Hz、50Hz、100Hz和200Hz的损耗测量数据；对于SMC材料,采用20Hz、100Hz和200Hz的损耗测量数据进行辨识。

图4是无取向钢片和SMC两种材料20～200Hz的Bm-P损耗曲线，通过Steinmetz公式得到的计算值的拟合结果和测量结果吻合较好。SMC铁耗在低磁通密度时远高于无取向钢片，随着频率升高，铁耗中涡流损耗占比不断增大，两者的总铁耗差距缩小。当交变励磁频率为200Hz时，SMC铁耗高于35WW270一倍。

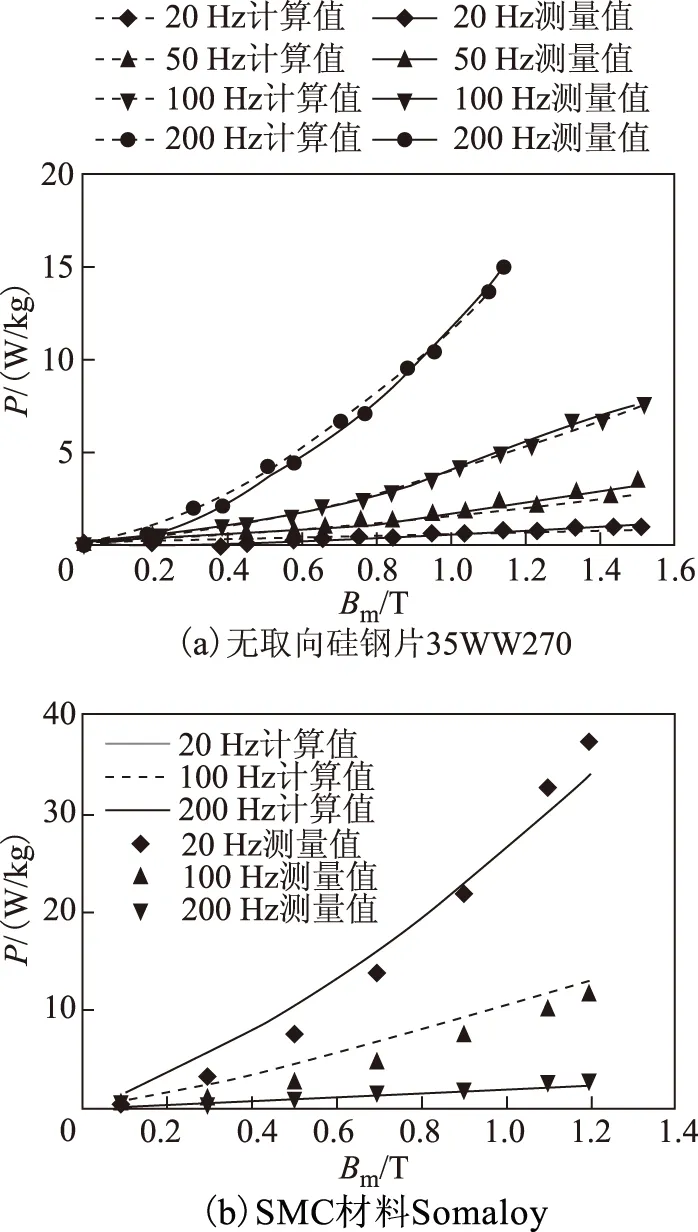
图4 两种材料的Bm-P曲线Fig.4 Bm-P curves of two materials

表1为无取向钢片和SMC材料的Steinmetz损耗系数，是通过在宽频(20～200Hz)下的交变损耗曲线拟合得到。该模型认为拟合的损耗系数不随频率的变化而变化，但是总损耗与频率的关系是β倍频、2倍频和1.5倍频三部分的组合关系。SMC材料的磁滞损耗系数远大于无取向硅钢片，SMC异常损耗系数小于无取向钢片。根据实验数据，两者涡流损耗系数相差不大。SMC材料的涡流损耗机制复杂，不仅依赖于微小铁基颗粒的尺寸而且依赖绝缘层的绝缘性能；既存在铁基小颗粒内部的微观涡流，也存在穿过绝缘层的宏观涡流[22]。

表1 两种材料的损耗系数

对于硅钢片材料,当交变励磁或旋转励磁时，硅钢片内部涡流Jx和Jy仅在沿叠片方向有显著变化，在平行叠片的平面内变化不显著。任意复杂励磁下，硅钢叠片的三维涡流场问题可分解为x、y方向的独立交变磁化过程，分别用一维涡流方程描述[23]，因此涡流损耗也可相应地分解为x、y方向交变涡流损耗。类似地，假设异常损耗也可分解为x、y方向独立的交变异常损耗，使用交变损耗辨识的kc、ke系数。故瞬时涡流损耗功率和异常损耗功率分别表示为

(23)

(24)

根据式(23)和式(24)，从测量的总铁耗中去除涡流损耗和异常损耗部分，剩余部分即不随频率变化的磁滞损耗，采用本文算法进行模型验证。

2.2 旋转损耗模型参数辨识

软磁材料的旋转磁特性测量方法没有统一的国际标准，国内外实验室广泛采用控制圆形或椭圆形B轨迹的励磁模型为

(25)

式中，εy为椭圆轨迹轴比。标准的圆形磁轨迹(εy=1)不包含谐波，易于损耗建模和特征参数的提取，同时反映软磁材料磁各向异性和旋转磁损耗特性。当εy=0时，励磁模型退化为单轴的交变励磁，反映了软磁材料的单轴交变损耗特性。在电力变压器的T型接口处，磁通密度的轨迹接近菱形，可采用椭圆形磁通密度轨迹近似模拟。

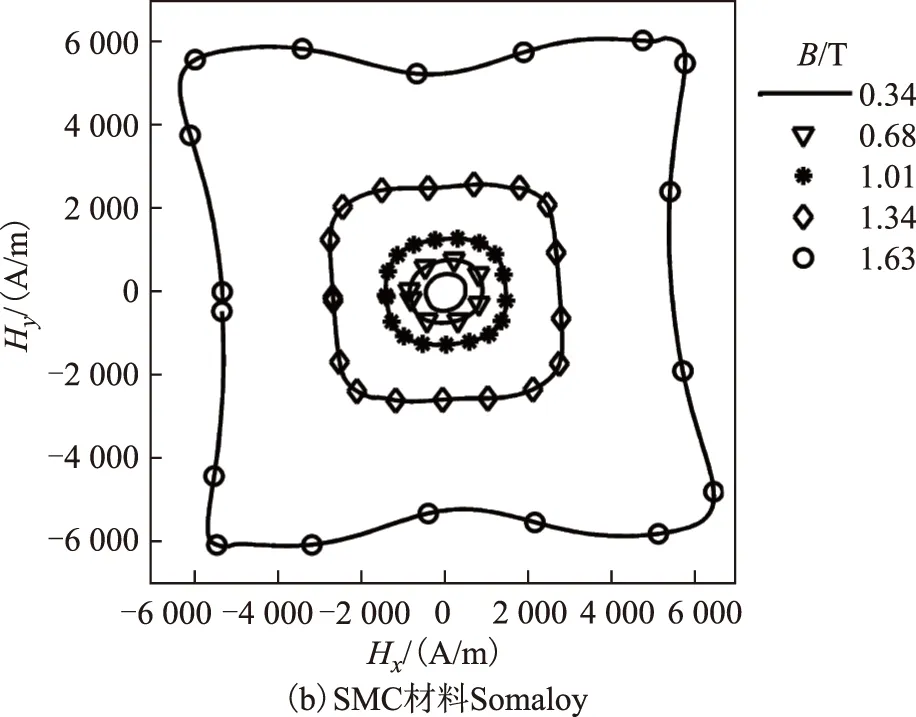
图5 圆形激励下50 Hz磁场强度轨迹Fig.5 Trajectory of 50 Hz magnetic field under circular excitation

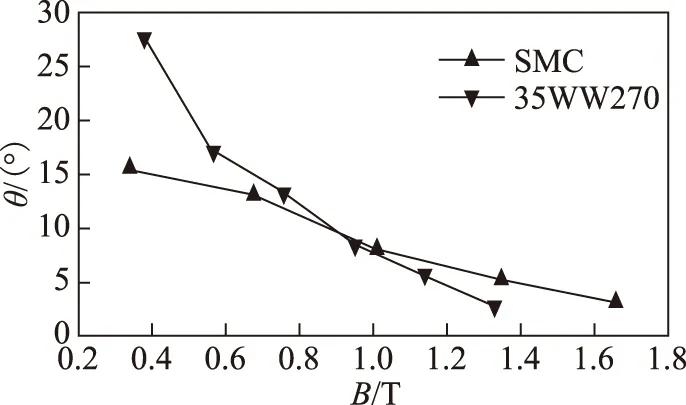
图6 旋转磁化磁通密度幅值与空间夹角关系Fig.6 Relationship between amplitude and space angle of the rotation magnetization

3 旋转损耗模型实验验证

3.1 三维磁特性测量

三维磁测量装置的主磁路由三对正交的C型铁心和六个多层柔性励磁线圈组成，如图7所示[21]。励磁装置的测量样品是SMC样品或硅钢叠片。样品切割或叠置为边长为22mm的立方体，放置于B-H复合立方体传感箱内，B-H线圈的尺寸和形状如图8所示，样品四周相距1mm，是匀场保护层，保护层的材料和叠置方向与样品相同，匀场保护层作为磁测量样品的延伸，Ansys-Maxwell的磁场仿真结果表明保护层磁场分布不均匀，但在样品表面获得了均匀的磁场，从而避免磁场的边缘效应。

图7 三维磁特性测量装置主磁路Fig.7 Three dimensional excitation core structure

图8 B-H线圈的尺寸和形状Fig.8 Size and shape of B-H coil

三维磁测量系统的任意椭圆宽频励磁模型为

(26)

式中，Ix、Iy分别为x、y轴励磁电流；εy为椭圆轨迹轴比。三维磁特性测量系统采用自适应的数字控制算法[24]。以工控机为控制核心，通过多功能采集卡发出三路模拟控制信号，经三路功率放大器和阻抗匹配电路放大获得大励磁电流，在测量样品的内部(SMC或硅钢叠片)生成交变或旋转的磁场，从而测量不同励磁模式下软磁材料的磁各向异性和损耗特性。

3.2 磁损耗的测量和模型验证

本文提出的磁滞损耗计算模型同时兼顾交变磁滞损耗和旋转磁滞损耗。采用三维磁特性测量装置对无取向钢片进行多种励磁模式的损耗测量。首先，通过一组交变磁化实验和一组圆形磁化实验辨识损耗模型的参数；其次，利用不同轴比椭圆轨迹下的损耗特性验证本文损耗模型的有效性。

图9 对比了四种磁特性测量实验下的铁心总损耗，磁滞损耗部分采用本文提出的损耗模型，经典涡流损耗和异常损耗分别采用式(23)和式(24)进行建模分析。根据励磁模型式(25)，四组实验磁通密度轨迹分别是εy=0、1、1/2、1/4，轨迹的形状通过磁场反馈控制算法保证。图9a是x轴交变损耗实验结果及两种模型的预测结果，因为两种模型的参数都依赖交变励磁实验结果，故两种模型都能够很好地逼近测量结果。图9b是圆形旋转磁化的实验结果，本文模型的参数使用该组测量数据进行辨识，故两种模型与实验结果吻合很好。而基于Steinmetz的方法认为旋转磁化是两个方向独立交变磁化的叠加。铁磁学的物理磁化过程是当软磁材料接近饱和时，旋转磁化的磁性材料磁畴逐渐减少至消失，因此磁滞损耗部分接近于零，故旋转磁特性实验损耗低于两个方向交变的磁特性损耗之和，Steinmetz方法计算的预测旋转损耗高于测量旋转损耗，即为模型的主要缺陷。本文模型能够直接从旋转磁化角度建模分析，与实验结果吻合较好。图9c和图9d是不同轴比的椭圆激励的测量结果，混合激励下的磁畴壁运动行为复杂，既有磁畴壁的平动也包含磁畴壁的转动，基于Steinmetz的模型仅假设两个方向独立的磁畴壁移动，其预测损耗结果低于实际测量结果和本文模型预测结果。

图9 不同励磁模式下模型预测值与实验值对比Fig.9 Comparison of model predictions and experimental values under different excitation modes

综上，对于四种不同的励磁模型，本文提出的损耗预测方法与实验结果误差较小，尤其在旋转励磁下，明显优于传统的Steinmetz方法。

4 结论

本文提出一种旋转磁滞损耗模型，并对SMC材料和无取向硅钢片进行实验验证，详细阐述了磁滞损耗模型原理及其实现过程。该模型有如下优点：

1)统一了交变损耗和旋转损耗模型，实现了任意轨迹二维磁滞损耗的计算。

2)损耗模型是基于瞬态实现的，无需存储全过程的磁化历史并计算处理，故占用内存少，而且易于集成到电磁有限元分析中。

3)能够计算过度饱和状态下旋转磁滞损耗，此时旋转磁滞损耗显著下降，铁耗主要包括涡流损耗和剩余损耗两部分，该方法比Steinmetz方法有更高的精度。

[1] 佟文明, 朱晓锋, 朱龙飞, 等. 不同供电方式对非晶合金永磁同步电机铁耗的影响[J]. 电工技术学报, 2015, 30(10): 10-18.TongWenming,ZhuXiaofeng,ZhuLongfei,etal.Theimpactofdifferentsupplymodesoncorelossesofamorphousalloypermanentmagnetsynchronousmotor[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(10): 10-18.

[2]BerotttiG.Hysteresisinmagnetismforphysicists,materialsscientists,andengineers[M].NewYork:AcademicPress, 1998.

[3]ReinertJ,BrockmeyerA,DonckerRD.Caculationoflossesinferro-andferromagneticmaterialsbasedonthemodifiedsteinmetzequation[J].IEEETransactionsonIndustryApplications, 2001, 37(4): 1055-1061.

[4]AbdallahJ,SullivanC.Improvedcalculationofcorelosswithnonsinusoidalwaveforms[C]//Thirty-SixthIASAnnualMeeting, 2001, 4: 2203-2210.

[5]IonelD,DellingerSJ,MillerTJE,etal.Onthevariationwithfluxandfrequencyofthecorelosscoefficientsinelectricalmachines[J].IEEETransactionsonIndustryApplications, 2006, 42(3): 658-667.

[6] 赵志刚, 程志光, 刘福贵, 等. 基于漏磁通补偿的导磁钢板直流偏磁杂散损耗特性模拟[J]. 电工技术学报, 2015, 30(8): 38-44.ZhaoZhigang,ChengZhiguang,LiuFugui,etal.ModelingoftheDC-biasedstray-fieldlossofmagneticsteelplatebasedoncompensatorofleakageflux[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(8): 38-44.

[7]ZhuJianguo,RamsdenVS.Improvedformulationsforrotationalcorelossesinrotatingelectricalmachines[J].IEEETransactionsonMagnetics, 1998, 34(4): 2234-2242.

[8] 李丹丹, 刘福贵, 李永建, 等. 一种新的混合矢量磁滞模型磁滞算子定义方法[J]. 电工技术学报, 2014, 29(11): 1-7.LiDandan,LiuFugui,LiYongjian,elal.Anewdefinitionmethodofthehysteroninhybridvectorhysteresismodel[J].TransactionsofChinaElectrotech-nicalSociety, 2014, 29(11): 1-7.

[9] 傅伟, 赵莉华, 梁勇, 等. 多台变压器空载合闸励磁涌流及抑制方案的研究[J]. 电力系统保护与控制, 2015, 43(1): 28-33.FuWei,ZhaoLihua,LiangYong,etal.Studyonno-loadclosinginrushcurrentoftransformergroupandsuppressionmeasures[J].PowerSystemProtectionandControl, 2015, 43(1): 28-33.

[10]姚东晓, 邓茂军, 倪传坤, 等. 变压器多侧励磁涌流产生机理及对差动快速动作区影响研究[J]. 电力系统保护与控制, 2016, 44(5): 36-41.YaoDongxiao,DengMaojun,NiChuankun,etal.Transformer′smulti-sideinrushcurrentgenerationmechanismanditsinfluenceonthedifferentialprotection′sfastactionzone[J].PowerSystemProtectionandControl, 2016, 44(5): 36-41.

[11]EnokizonoM,SodaN.DirectmagneticlossanalysisbyFEMconsideringvectormagneticproperties[J].IEEETransactionsonMagnetics, 1998, 34(5): 3008-3011.

[12]LinDingsheng,ZhouPing,BergqvistA.Improvedvectorplaymodelandparameteridentificationformagnetichysteresismaterials[J].IEEETransactionsonMagnetics, 2014, 50(2): 357-60.

[13]赵小军, 崔灿, 李琳, 等. 基于定点谐波平衡法的铁心磁滞与损耗特性分析[J]. 电工技术学报, 2014, 29(7): 10-18.ZhaoXiaojun,CuiCan,LiLin,etal.Analysisofthehysteresisandlosscharacteristicsinthelaminatedcorebyfixedpointharmonic-balancedmethod[J].TransactionsofChinaElectrotechnicalSociety, 2014, 29(7): 10-18.

[14]赵海森, 罗应立, 刘晓芳, 等. 异步电机空载铁耗分布的时步有限元分析[J]. 中国电机工程学报, 2010, 30(30): 99-106.ZhaoHaisen,LuoYingli,LiuXiaofang,etal.Analysisonno-loadironlossesdistributionofasynchronousmotorswithtime-steppingfiniteelementmethod[J].ProceedingsoftheCSEE, 2010, 30(30): 99-106.

[15]ZhouPing,LinDingsheng,LuChuan,etal.Anewalgorithmtoconsidertheeffectsofcorelosseson3-Dtransientmagneticfields[J].IEEETransactionsonMagnetic, 2014, 50(2): 365-368.

[16]PfutznerH,MulasalihovicE,YamaguchiH,etal.Rotationalmagnetizationintransformercores-areview[J].IEEETransactionsonMagnetics, 2011, 47(11): 4523-4533.

[17]SievertJ.Recentadvancesintheone-andtwo-dimensionalmagneticmeasurementtechniqueforelectricalsheetsteel[J].IEEETransactionsonMagnetics, 1990, 26(3): 2553-2558.

[18]ZurekS,RygalR,SoinskiM.Asymmetryofmagneticpropertiesofconventionalgrain-orientedsteelwithrelationto2Dmeasurement[J].PrzegladElektrotech-niczny, 2009, 85(1): 16-19.

[19]LiYongjian,LinZhiwei,LiuHongxun,etal.Three-dimensionalmagneticpropertiesofsoftmagneticcompositematerialatdifferentfrequencies[J].JournalofAppliedPhysics, 2010, 109(7): 07B503.

[20]张艳丽, 何厚建, 谢德馨, 等. 基于二维磁特性测量的电工钢片矢量磁滞模型[J]. 中国电机工程学报, 2010, 30(3): 130-135.ZhangYanli,HeHoujian,XieDexin,etal.Vectormagnetichysteresismodelofelectricalsteelsheetsbasedontwo-dimensionalmagneticpropertymeasurement[J].ProceedingsoftheCSEE, 2010, 30(3): 130-135.

[21]LiYongjian,YangQingxin,ZhuJianguo,elal.Designandanalysisofanovel3-Dmagnetizationstructureforlaminatedsiliconsteel[J].IEEETransactionsonMagnetics, 2014, 50(2): 389-392.

[22]KollarP,BircakovaZ,FuzerJetal.PowerlossseparationinFe-basedcompositematerials[J].JournalofMagnetismandMagneticMaterials, 2013, 327(2): 146-150.

[23]DlalaE.Comparisonofmodelsforestimatingmagneticcorelossesinelectricalmachinesusingthefinite-elementmethod[J].IEEETransactionsonMagnetics, 2009, 45(2): 716-725.

[24]ZurekS,MarketosP,MeydanT,etal.Useofnoveladaptivedigitalfeedbackformagneticmeasurementsundercontrolledmagnetizingconditions[J].IEEETransactionsonMagnetics, 2005, 41(11): 4242-4249.

(编辑 张洪霞)

Measurement and Modeling of Rotational Hysteresis Loss ofElectric Soft Magnetic Material

ZhangChanggeng1YangQingxin1,2LiYongjian1

(1.Province-Ministry Joint Key laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology Tianjin 300130 China 2. Tianjin Key Laboratory of Advanced Technology of Electrical Engineering and Energy Tianjin Polytechnic University Tianjin 300387 China)

The rotational flux in the core of power transformer and motor causes the inaccuracy efficiency computation of magnetic apparatus. In order to address the problem, this work focuses on magnetic measurement of rotational magnetization and its hysteresis loss modeling. Firstly, the vector hysteresis loss is decomposed into the transverse and radial components which are defined based on rotational loss and alternating loss, respectively. Secondly, the model parameters of soft magnetic composites and non-oriented silicon steel are identified. Their magnetic properties and model parameters are compared and analyzed. Finally, a series of complex excitation magnetization experiments on non-oriented silicon steel are carried out. The measurement results are compared with the predicted values by the model. It shows that the proposed model gives more exact predicted results than the traditional Steinmetz method.

Motor core loss，hysteresis loss，electro-magnetic simulation，rotational loss

国家自然科学基金资助项目(51237005，51507045)。

2016-03-30 改稿日期2016-05-05

TM15

张长庚 男，1985年生，博士研究生，研究方向为工程电磁场与磁技术、三维磁特性测量与建模。

E-mail：chang_geng@sina.com

李永建 男，1978年生，教授，研究方向为工程电磁场与磁技术、三维磁特性测量与建模。

E-mail：liyongjian@hebut.edu.cn(通信作者)