单相级联H桥整流电路非线性控制策略

孙玉巍 刘教民 李永刚 付 超 杨喆明

(新能源电力系统国家重点实验室(华北电力大学) 保定 071003)



单相级联H桥整流电路非线性控制策略

孙玉巍 刘教民 李永刚 付 超 杨喆明

(新能源电力系统国家重点实验室(华北电力大学) 保定 071003)

针对电力电子牵引变压器输入级单相级联H桥(CHB)整流电路的非线性及扰动工况，提出一种基于静止坐标系的非线性优化控制策略。根据系统仿射非线性模型及微分几何理论，提出基于部分反馈线性化的零动态设计方案，对其线性部分采用二次型最优方法以确定反馈增益，并引入谐振环节以实现零相差跟踪；对于零动态则采用基于扩张状态观测器的自抗扰控制策略，以提高系统在负载大范围扰动时的控制品质。实验结果表明，该控制策略能提高CHB系统在电网电压及负载扰动时的动态响应速度，保证网侧电流及直流电压快速稳定调节，同时使网侧在单位功率因数下运行，各模块直流电压均衡。

单相级联H桥 静止坐标 状态反馈 零动态 自抗扰控制

0 引言

基于电力电子及中高频大功率变压器技术的电力电子牵引变压器(Power Electronic Traction Transformer，PETT)能够实现轻量化、高功率密度、低谐波及能量交互，已成为国内外研究的热点[1-3]，而作为其输入级的单相级联H桥(Cascade H-Bridge，CHB)整流器则是PETT能够实现上述目标的关键。一方面，为获得“净化”的电力电子接口，需要对并网电流进行精确控制，实现网侧低谐波、单位功率因数运行；另一方面，由于PETT运行工况复杂，电网电压和负载扰动剧烈，要求系统具有较强的抗扰能力。

针对单相或三相PWM整流电路的非线性、强耦合，基于微分几何的非线性控制方法近年来受到了广泛关注[4-7]。通过适当的非线性状态反馈和坐标变换，可将非线性系统精确或部分线性化，从而采用线性系统的优化控制方法。文献[4]通过引入关系度为2的能量函数作为系统输出，实现了PWM整流器精确线性化，但将能量函数作为单一控制目标的方法仅适用于dq坐标系下有功电流指令为直流量的情况。文献[5，6]针对三相PWM整流电路，采用将并网电流精确线性化，而将直流电压作为零动态通过外环予以控制的方法，并在电压环分别引入变速积分及非线性抗扰积分以提高系统抗扰能力，这两种方法均借鉴了自抗扰控制(Active Disturbance Rejection Control，ADRC)非线性光滑反馈的优点，但没有涉及作为ADRC核心的扩张状态观测器(Extended State Observer，ESO)。ESO可实时估计系统状态及总和扰动信息，并用给予补偿的方法取代误差积分反馈作用[8，9]，对非线性、扰动剧烈的PETT应用场合具有较好的应用前景。此外，上述非线性控制方案均基于dq旋转坐标系，当用于单相CHB整流器时，还需构建正交虚拟电路以实现dq变换[10]，而本文CHB作为PETT输入级，只需要实现网侧单位功率因数运行，无需提供无功补偿功能，因此可采用简单的基于静止坐标系的控制方法。

为实现并网电流对电网电压的零相位差跟踪及对特定谐波的抑制，目前基于静止坐标系的PWM整流控制方法多为基于内模原理的重复控制[11，12]、比例谐振(PR)控制[13，14]。PR控制器的比例系数kp和谐振系数kr的整定，均依赖于系统近似线性化模型，当用于PETT大范围负载扰动工况时，其控制品质将难以保证；且kp、kr共同影响系统响应，当采用根轨迹法整定时，需要多族根轨迹进行分析，以实现两参数的相互配合取值，整定较困难[15]。

本文针对PETT输入级CHB电路静止坐标系模型提出基于部分反馈线性化的零动态控制策略。根据微分几何非线性理论，对系统状态反馈线性化过程进行详细推导，由此选择以并网电流为可控量，直流电压的二次方为零动态的设计方案。对于线性部分采用二次型最优方法确定反馈增益，并引入谐振环节以补偿系统相差；对零动态采用基于ESO的ADRC控制，以提高系统在负载大范围扰动时的控制品质。最后将所提控制策略应用于采用混合PWM(Hybrid PWM，HPWM)调制的5模块CHB系统，通过实验对其控制品质进行了验证。

1 系统建模及其状态反馈非线性控制

1.1 级联H桥整流器仿射非线性模型

级联式PETT拓扑如图1所示，由输入级CHB及后级隔离双向DC-DC变换器(Isolated Bidirectional DC-DC Converter，IBDC)构成，本文研究对象为前级CHB整流器，而将后级IBDC用等效负载电阻RL表示，vs和is分别为电网电压、电网电流，Ls为交流滤波电感，Rs为其等效电阻，van为CHB总的交流输出电压，vhi、vdci(i=1，2，…，N)分别为第i个模块的交流端电压及直流电压，C为直流电容，S1～S4为电力电子开关器件，各模块参数均相同。

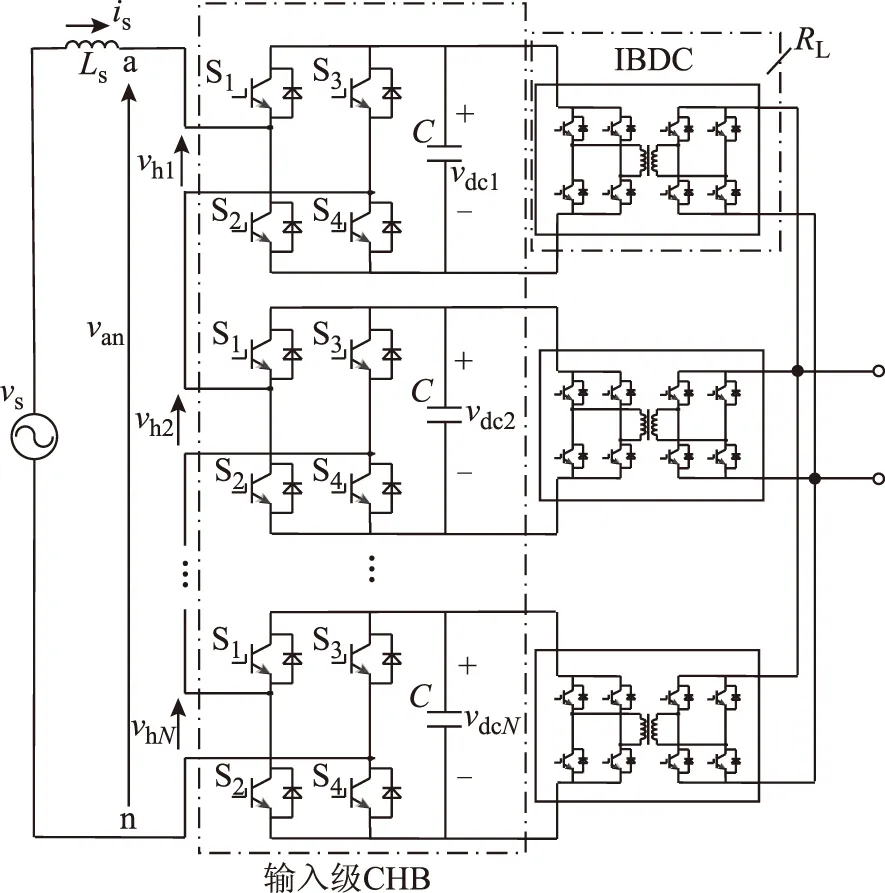
图1 级联式PETT主电路拓扑Fig.1 Main circuit topology of cascaded PETT

根据基尔霍夫定律，可列写CHB状态方程为

(1)

式中，hi为各H桥开关函数，i=1，…，N。当S1、S4导通时，hi=1；当S2、S3导通时，hi=-1；当S1、S3或S2、S4导通时，hi=0。

假设各直流电压均衡，即vdc1=vdc2=…=vdcN=vdc，vdc为各模块直流电压平均值，则系统状态方程为

(2)

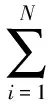
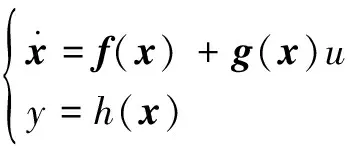
(3)

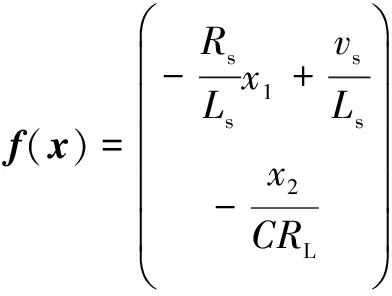
观察状态方程可知其对状态变量呈非线性，对控制变量呈线性，为仿射非线性系统。系统输出方程根据实际控制目标，可有多种选择，输出方程不同。决定系统的关系度不同。若关系度等于系统阶数，则可以采用状态反馈精确线性化设计方法；如果关系度小于系统阶数，则可采用部分反馈线性化零动态设计方法[16]。

1.2 状态反馈非线性控制原理

1)状态反馈精确线性化条件。

根据微分几何非线性控制理论[16，17]，式(3)所示仿射非线性系统可以实现状态反馈精确线性化，当且仅当存在一个区域Ω使得下列条件成立：

以上条件若满足，就必然存在一个输出函数ω(x)，使得在Ω上系统的关系度等于系统阶数n，该系统可以被完全精确线性化为可控的线性系统。

已知式(3)所示系统n=2，对其求Lie括号，有

(4)

(5)

可知矩阵[g，adfg]秩为2，条件(1)满足。又由于集合{g}是对合的，条件(2)也满足。因此可以找到一个函数ω(x)，使其满足条件Lgω(x)=0，LgLfω(x)≠0，即系统关系度为2，等于系统阶数。

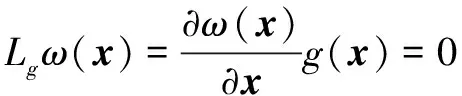
(6)

经验证：LgLfω(x)≠0，符合条件。

可见只有将输出函数选为关系度为2的能量函数时，式(3)才能实现精确线性化。而对于实际单相CHB系统，并网电流需要精确跟踪正弦指令，直流电压指令为直流量，如将能量函数作为直接控制对象，控制器设计困难，因此更适合选用以并网电流为输出函数的零动态设计方案。

2)零动态标准型。

选择并网电流与其参考值之差作为输出函数

y=h(x)=x1-iref

(7)

由Lgh(x)=-vdc/Ls≠0可知系统关系度为r=1，小于系统阶数2，又由系统满足条件(1)和条件(2)，根据非线性控制零动态设计原理，存在函数η(x)满足条件Lgη(x)=0，使得系统在坐标变换z=Φ(x)=[h(x)η(x)]T下，可转换为零动态标准型

(8)

式中，第一式为线性系统动态方程；第二式为零动态方程。根据实际系统可直接选择η(x)为零动态变量，也可以选择η(x)中的不可控部分为零动态变量，由式(6)可直接选取

(9)

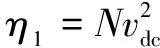
(10)

由式(10)可看出，零动态的特征根s=-2/(CRL)位于左半复平面，因此零动态渐近稳定。但若零动态不加控制，当负载电阻RL较大时，特征根离虚轴很近，直流电压的过渡时间将很长。为改善零动态在负载大范围扰动时的动态性能，本文采用基于ADRC的零动态控制策略，在第2.2节阐述。

2 CHB控制系统设计

2.1 基于状态反馈二次型最优及谐振补偿的并网电流控制策略

将式(8)第一式写成线性系统形式为

(11)

式中，A=0；B=1。选取二次型性能指标为

(12)

式(12)中第一项体现了控制过程中和终端时刻的状态误差趋近于0，第二项是对控制幅度的限制。因状态变量及预控变量为一维，权矩阵Q和R均为一个正数，设使性能指标为最小的最优控制为

v*=-K*z1

(13)

则反馈增益系数为K*=R-1BTP，P是Riccati矩阵方程PA+ATP-PBR-1BTP+Q=0的正定对称解。

对权矩阵Q的确定，取式(9)能量函数第一项构造性能指标，即

(14)

可得Q=Ls/2，并且选择权矩阵R=Ls2/f，f为系统等效开关频率。

将A、B、Q、R代入Riccati方程，可解得矩阵P和反馈增益K*，将求得的反馈增益代入式(13)、式(11)，即可得到原非线性系统的反馈控制律u为

(15)

式中，iref为并网电流指令，iref=Irefsin(ωt)，sin(ωt)为与电网电压同相位的正弦信号，Iref为并网电流幅值指令。

由式(15)所得并网电流非线性控制框图如图2a所示。由于输入iref为正弦变化量，若仅采用单增益状态反馈会产生跟踪相位差。对此，根据内模及重复控制原理[18]，本文在状态反馈环中引入谐振控制器Gr(s)，如图2b所示。谐振控制器传递函数为

(16)

式中，ωc为考虑实际系统实现及电网允许频率波动引入的带宽量，若电网频率允许波动范围为±0.8 Hz，ωc=1.6π=5 rad/s[15]。对于k′，根据以其为参量的单条根轨迹即可容易整定。

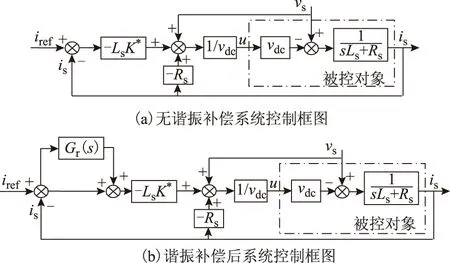
图2 并网电流非线性控制闭环框图Fig.2 The nonlinear closed loop control diagram of grid current

根据闭环特征方程相同的原则，由图2b可得以k′为开环增益的等效开环传递函数为

(17)

设系统参数Ls=8 mH，Rs=0.2 Ω，等效开关频率f=2 kHz，由Matlab lqr指令可计算反馈增益K*=790，代入式(17)，绘出以k′为参变量的系统根轨迹如图3所示，s1、s2、s3为特征根，选择阻尼比最大的极点(黑色方框中)，对应增益k′的值为40。

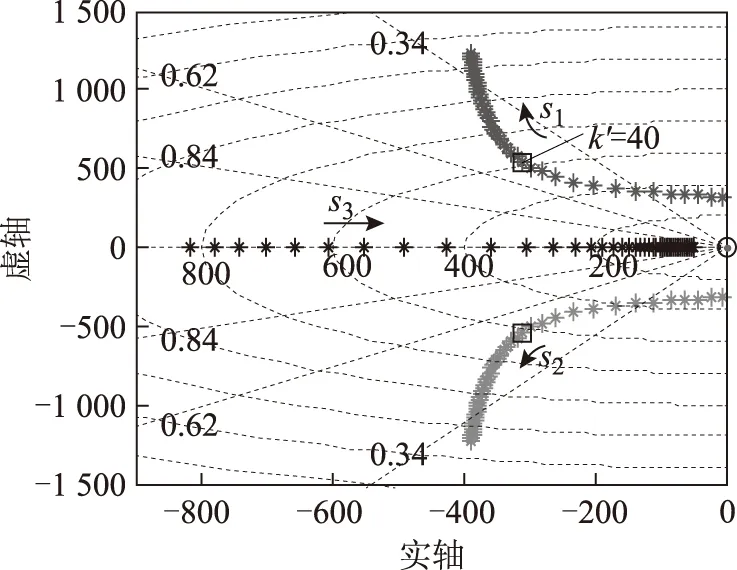
图3 以k′为参变量的系统根轨迹Fig.3 Root locus of the system depending on parameter k′

2.2 基于ADRC的零动态控制

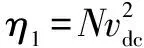
将式(10)中网侧瞬时功率vsiref用有功功率vmIref/2代替，vm为电网电压幅值，零动态方程可写为

(18)

式中，u′为并网电流幅值指令，u′=Iref；f为由系统内部不确定性及外部扰动共同作用的总扰动项[8]，采用二阶非线性ESO进行估计，表达式为

(19)

式中，γ1为η1的观测值；γ2为对总扰动项f的估计值；β1、β2为观测器增益；采用非线性函数fal(e，α，δ)可避免高频振颤现象的出现，其中α为非线性因子，δ为滤波因子。fal(e，α，δ)函数表达式为

(20)

在ESO对系统状态及总扰动能获得较好估计的基础上，令

(21)

则零动态方程可转换为典型一阶线性系统

=kp(η1ref-η1)

(22)

式中，kp为系统带宽，kp越大，调节时间ts越短，考虑PWM控制、采样延迟而留取一定裕量，本文取kp≈5/ts，若需ts为0.1 s时，kp为50。

对于ESO非线性函数参数α、δ，根据文献[8]对fal(e，α，δ)的大量测试，要求0<α<1，其值越小非线性越强，本文取α1=0.25，α2=0.5，滤波因子δ=0.01。对于ESO反馈增益β1和β2，采用线性极点配置方法，忽略式(19)中非线性函数，令β1=2ω0，β2=ω02[19]，ω0为二阶线性ESO带宽，要求其必须大于反馈控制器带宽kp，考虑采样速率及噪声容限，本文选ω0=4kp。

根据图2及2.2节对CHB整流器非线性电流环及自抗扰零动态控制器的设计，可得CHB整体控制策略如图4所示，图中PLL表示锁相环，CHB采用HPWM调制技术，具体见第4节。

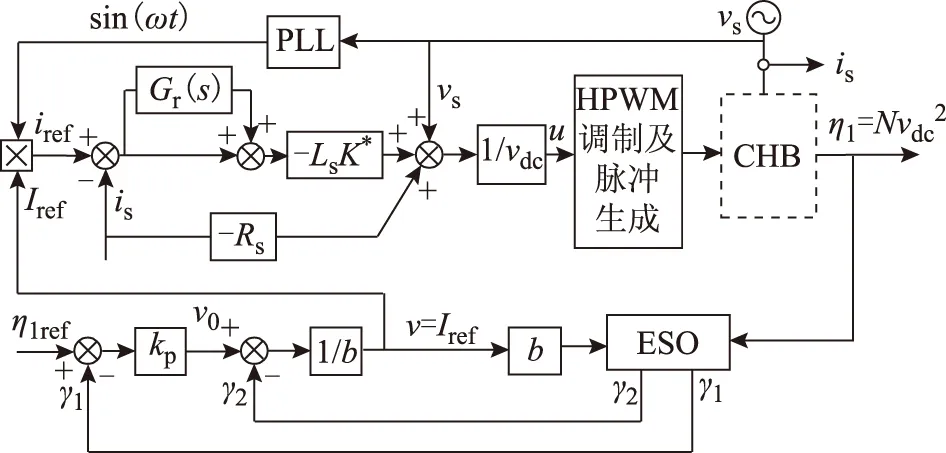
图4 CHB整流器整体控制策略Fig.4 Overall control strategy of the CHB rectifier

3 HPWM调制策略

在上述控制策略生成总占空比调制信号u的基础上，为降低系统开关频率，采用阶梯波与PWM相结合的HPWM调制方法[20]，基本原理如图5所示。利用N-1个模块工作于阶梯波模式，1个模块工作于PWM模式，两者输出波形叠加，即可得到2N+1电平PWM电压波形，该方法可降低系统整体开关频率，且保证波形质量。

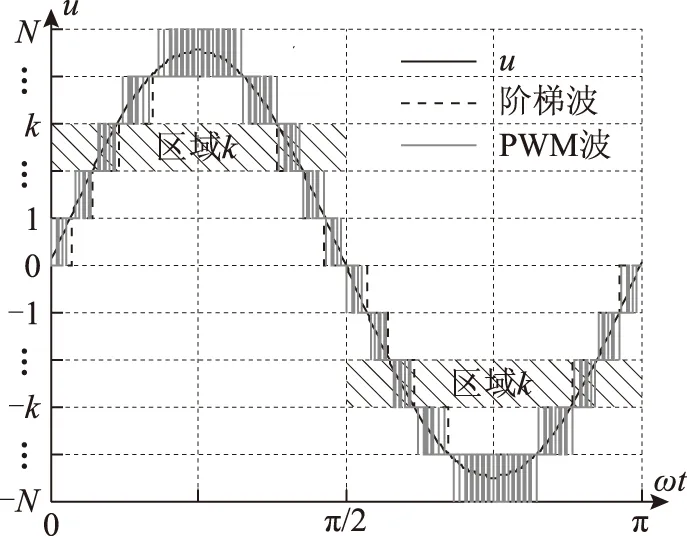
图5 HPWM调制原理Fig.5 Principle of HPWM modulating strategy

HPWM调制实现方法可描述为：

首先将总调制信号u进行取整运算以得到当前多电平电压区域k为

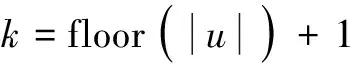
(23)

式中，floor(·)为向低取整的函数，k=1,2,…,N。

然后将各模块直流电压进行排序，并根据当前k值、调制信号u及并网电流is极性，确定各模块开关函数hi，以保证直流电压均衡。基于电压排序的HPWM算法实施流程如图6所示，可描述为：

1)当u>0，is>0，令直流电压较低的k-1个模块工作于+1开关模式，第k个模块工作于PWM模式，其余工作在0模式。

2)当u>0，is<0，令直流电压较高的k-1个模

块工作于+1开关模式，第k个模块工作于PWM模式，其余工作于0模式。

3)当u<0，is>0，令直流电压较高的k-1个模块工作于-1开关模式，第k个模块工作于PWM模式，其余工作于0模式。

4)当u<0，is<0，令直流电压较低的k-1个模块工作于-1开关模式，第k个模块工作于PWM模式，其余工作于0模式。

工作于PWM模式的H桥调制波ut为

ut=u-(k-1)sign(u)

(24)

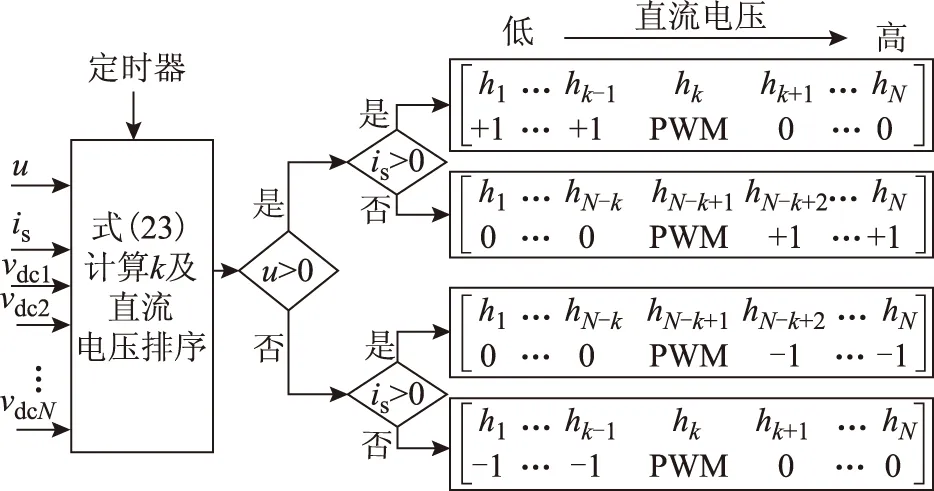
图6 HPWM调制算法流程Fig.6 Flowchart of the HPWM algorithm

4 实验验证

搭建小功率5模块级联CHB实验平台，如图7所示，其中HB1～HB5为5个H桥模块，控制器采用DSP+FPGA架构，DSP28335主要实现控制算法，FPGA采用XilinxXC3S400芯片，主要负责采样、通信和PWM脉冲生成。

实验参数：电网电压vs频率为50 Hz，其有效值由160 V阶跃至200 V，滤波电感Ls=8 mH，内阻Rs=0.2 Ω，直流侧电容C=20 mF，vdcref=60 V，负载扰动时，模块等效负载电阻由50 Ω切换为25 Ω；HPWM调制载波频率fc=2 kHz。

图7 5模块CHB整流器实验平台Fig.7 Laboratory setup of the five-module CHB rectifier

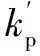
图8为两种控制策略电网电压扰动时网侧和直流电压实验波形对比，负载不变。图8a、图8b为网侧波形结果，包括并网电流is、电网电压vs及多电平交流电压van；图8c、图8d为直流电压波形对比。由实验录波得到相应的对比结果见表1。可知当电网电压扰动时，两种控制策略并网电流均可由原稳态值3.3 A过渡至新稳态值2.6 A，在本文控制策略下，并网电流调节时间仅为15 ms(0.75个周波)，而PR-PI控制下约为70 ms(3.5个周波)。对于直流电压波形，当电网电压扰动时，本文控制策略下直流电压几乎无明显突变；而PR-PI控制下约有3 V的上升，经约300 ms恢复稳态60 V，表明本文控制策略抗扰能力较强。两种控制策略下稳态波形相差不大，在200 V额定电网电压下，多电平输出电压van为11电平波形，总谐波畸变率(THD)均约为13.4%，经交流滤波电感滤波后，稳态并网电流波形THD仅为2.7%，且与电网电压同相位。

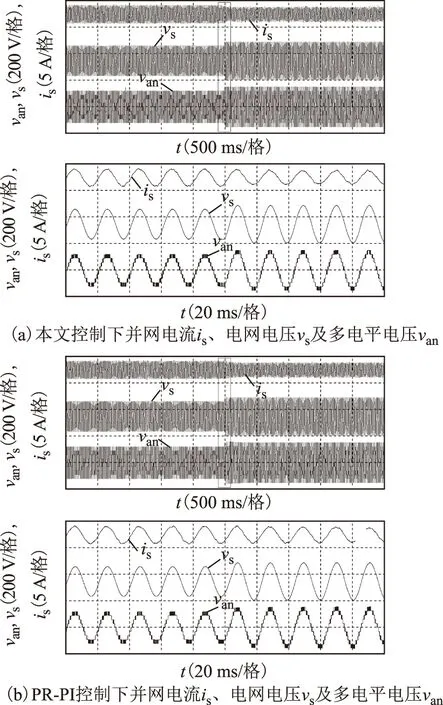
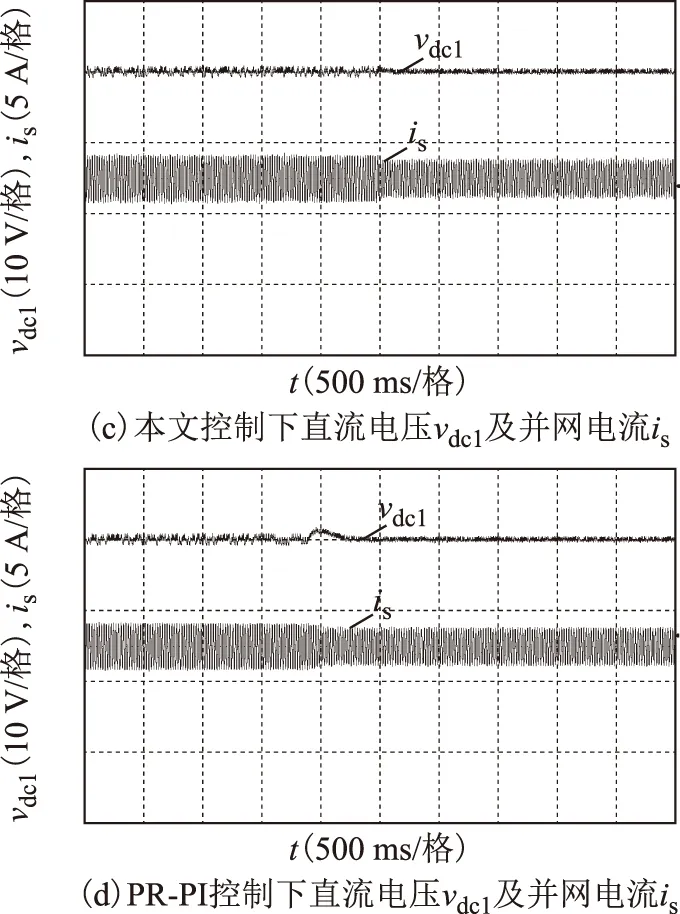
图8 两种控制策略下电网电压扰动实验结果比较Fig.8 Comparison of experimental results between two control methods under grid voltage disturbed case

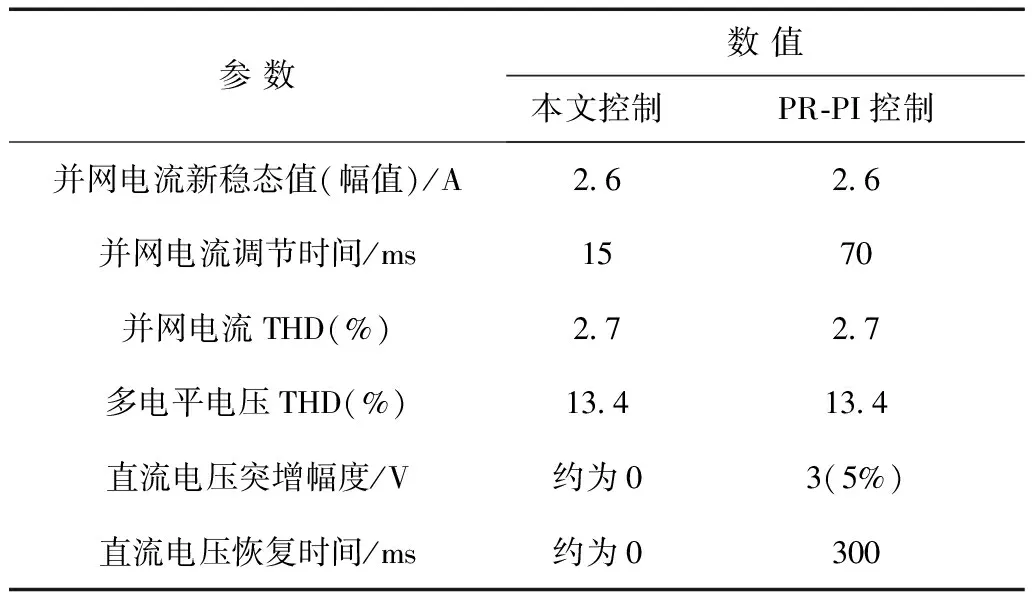
表1 两种控制策略电网电压扰动下实验结果对比

图9为两种控制策略在加载扰动时(负载功率由360 W增加至720 W)的实验对比结果。由实验录波得到相应的对比结果见表2，可知当负载扰动时，两种控制策略下并网电流均可由原稳态值2.6 A过渡至新稳态值5.2 A，但本文控制下并网电流调节时间仅为15 ms(0.75个周波)，而PR-PI控制下调节时间约为40 ms(2个周波)。对于直流电压波形，当负载增加时，本文控制下直流电压仅下降2 V，经100 ms即可恢复；而PR-PI控制下直流电压下降幅度约为5 V，经150 ms恢复。该结果表明所提控制策略对负载扰动具有较好的控制品质。

图10为本文控制策略下5个模块直流电压波形，均稳定在参考值60 V，加载之前电压纹波约2.5%，负载增加后，导致电容充、放电电流亦增加，因此电压纹波增加至4%。该结果表明文中基于电压排序的HPWM调制算法可有效实现直流电压的均衡。

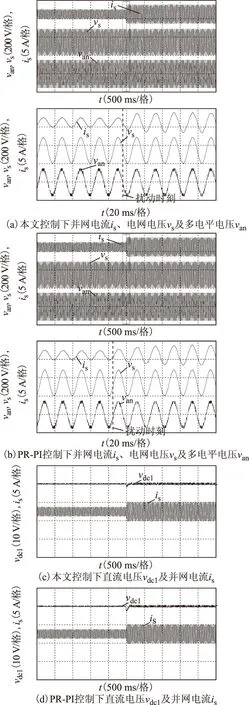
图9 两种控制算法下负载扰动时实验结果比较Fig.9 Comparison of experimental results between two control methods under load disturbed case

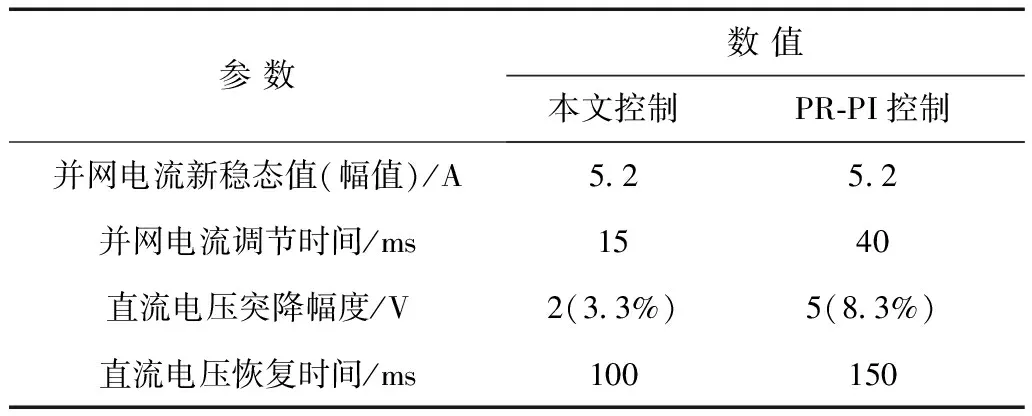
参数数值本文控制PR⁃PI控制并网电流新稳态值(幅值)/A5 25 2并网电流调节时间/ms1540直流电压突降幅度/V2(3 3%)5(8 3%)直流电压恢复时间/ms100150

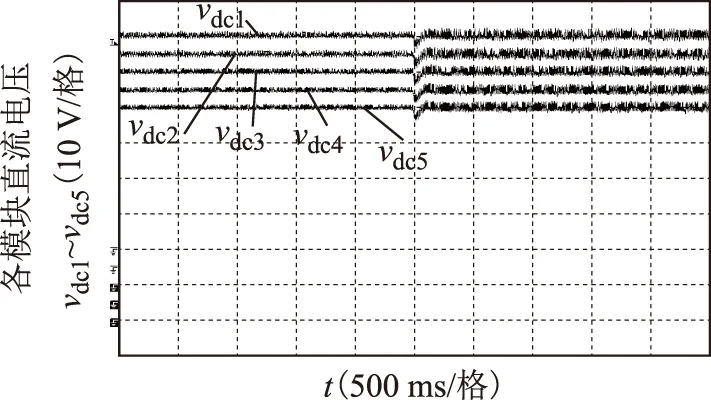
图10 本文控制算法下5个模块直流电压波形Fig.10 Waveforms of dc voltages of the five modules under the proposed control strategy

5 结论

本文对CHB系统基于静止坐标系的非线性控制策略进行研究，提出以并网电流为可控量、直流电压平方量为零动态的部分反馈线性化零动态控制方案。

1)对系统线性化部分采用二次型最优方法以确定反馈增益，并在反馈环引入谐振控制以实现电流零相位差跟踪，由于反馈增益已确定，谐振系数可在系统全局线性化模型的基础上，通过根轨迹法进行整定，由于参量只有一个，因而整定过程较容易。

2)选择直流电压二次方量为零动态，可得到一阶零动态方程，进而采用一阶ADRC控制器，控制算法易于实现；且可提高系统在负载大范围扰动时的控制品质，对PETT时变负载场合具有较好的应用价值。

[1] 李伟，张黎.铁道牵引单相电力电子变压器及控制[J].铁道学报，2013，35(4)：37-42. Li Wei，Zhang Li.Railway traction single-phase power electronics transformer and control[J].Journal of the China Railway Society，2013，35(4)：37-42.

[2] Dujic D，Zhao Chuanhong，Mester A，et al.Power electronic traction transformer-low voltage prototype[J].IEEE Transactions on Power Electronics，2013，28(12)：5522-5533.

[3] 律方成，郭云翔，付超，等.基于磁链分区的大功率中频变压器漏感参数计算方法[J].电工技术学报，2016，31(5)：164-169. Lü Fangcheng，Guo Yunxiang，Fu Chao，et al.Calculation method for leakage inductance of high power medium frequency transformers based on flux linkage partition[J].Transactions of China Electrotechnical Society，2016，31(5)：164-169.

[4] 孟建辉，石新春，付超，等.三相VSG系统的高性能非线性控制策略[J].中国电机工程学报，2014，34(6)：863-871. Meng Jianhui，Shi Xinchun，Fu Chao，et al.A high-performance nonlinear control strategy of three-phase VSG systems[J].Proceedings of the CSEE，2014，34(6)：863-871.

[5] 孟建辉，石新春，王毅，等.VSG系统直流电压快速稳定的控制策略研究[J].电工技术学报，2014，29(8)：219-226. Meng Jianhui，Shi Xinchun，Wang Yi，et al.Research on a fast and stable DC voltage control strategy of voltage sag generator system[J].Transactions of China Electrotechnical Society，2014，29(8)：219-226.

[6] 张晓华，郭源博，周鑫，等.PWM整流器的欠驱动特性与非线性控制[J].中国电机工程学报，2011，31(33)：85-92. Zhang Xiaohua，Guo Yuanbo，Zhou Xin，et al.Underactuated property and nonlinear control for PWM rectifier[J].Proceedings of the CSEE，2011，31(33)：85-92.

[7] 屈克庆，李文旗，叶天凯，等.基于状态反馈的LCL型逆变器解耦控制策略[J].电工技术学报，2016，31(20)：130-137. Qu Keqing，Li Wenqi，Ye Tiankai，et al.State feedback based decoupling control strategy for grid-connected inverter with LCL filter[J].Transactions of China Electrotechnical Society，2016，31(20)：130-137.

[8] 韩京清.自抗扰控制技术—估计补偿不确定因素的控制技术[M].北京：国防工业出版社，2013.

[9] 刘英培，梁海平，栗然.基于无源性与自抗扰控制的双馈风力发电系统研究[J].电工技术学报，2015，30(18)：122-130. Liu Yingpei，Liang Haiping，Li Ran.Research on doubly-fed wind power generation with passivity-based control and active disturbance rejection control[J].Transactions of China Electrotechnical Society，2015，30(18)：122-130.

[10]孙毅超，赵剑锋，季振东，等.一种基于虚拟电路闭环的单相PWM整流器控制新方法[J].电工技术学报，2013，28(12)：222-230. Sun Yichao，Zhao Jianfeng，Ji Zhendong，et al.A novel closed-loop control approach for single-phase PWM rectifier based on virtual circuit[J].Transactions of China Electrotechnical Society，2013，28(12)：222-230.

[11]张学广，马彦，李瑞，等.两相静止坐标系下并网逆变器的重复控制策略[J].电工技术学报，2016，31(9)：85-91. Zhang Xueguang，Ma Yan，Li Rui，et al.Repetitive control strategy for grid-connected converters in stationary frame[J].Transactions of China Electrotechnical Society，2016，31(9)：85-91.

[12]赵学华，史丽萍，陈丽兵.基于复合控制的改进型级联STATCOM控制策略[J].电力系统保护与控制，2015，43(17)：98-106. Zhao Xuehua，Shi Liping，Chen Libing.A new current control strategy of cascaded STATCOM with composite control[J].Power System Protection and Control，2015，43(17)：98-106.

[13]郭小强，贾晓瑜，王怀宝，等.三相并网逆变器静止坐标系零稳态误差电流控制分析及在线切换控制研究[J].电工技术学报，2015，30(4)：8-14. Guo Xiaoqiang，Jia Xiaoyu，Wang Huaibao，et al.Analysis and online transfer of stationary frame zero steady-state error current control for three-phase grid-connected inverters[J].Transactions of China Electrotechnical Society，2015，30(4)：8-14.

[14]陈素华.基于多载波和PR控制实现变换器并联环流抑制研究[J].电力系统保护与控制，2016，44(11)：129-134. Chen Suhua.Multicarrier PWM and PR control strategy of circulating current reduction for grid-connected converters[J].Power System Protection and Control，2016，44(11)：129-134.

[15]黄华，周波达，费建平，等.基于根轨迹法的链式STATCOM比例谐振电流控制器设计[J].江苏电机工程，2015，34(2)：1-9. Huang Hua，Zhou Boda，Fei Jianping，et al.Design of current proportional-resonant controller for chained STATCOM basing on root-locus method[J].Jiangsu Electrical Engineering，2015，34(2)：1-9.

[16]Isidori A.非线性控制系统[M].王奔，庄圣贤，译.北京：电子工业出版社，2005：172-228.

[17]卢强，梅生伟，孙元章.电力系统非线性控制[M].北京：清华大学出版社，2008：56-108.

[18]杨云虎，周克亮，程明，等.单相PWM变换器相位补偿谐振控制方案[J].电工技术学报，2013，28(4)：65-71. Yang Yunhu，Zhou Keliang，Cheng Ming，et al.Phase compensation resonant control scheme for single phase PWM converters[J].Transactions of China Electrotechnical Society，2013，28(4)：65-71.

[19]Gao Zhiqiang.Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the American Control Conference，Denver，Colorado，2003：4989-4996.

[20]Iman-Eini H，Schanen，J L，Farhangi S，et al.A modular strategy for control and voltage balancing of cascaded H-bridge rectifiers[J].IEEE Transactions on Power Electronics，2008，23(5)：2428-2442.

(编辑 赫蕾)

Nonlinear Control Strategy of Single-Phase Cascade H-Bridge Rectifier

SunYuweiLiuJiaominLiYonggangFuChaoYangZheming

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Baoding 071003 China)

A static coordinate based nonlinear optimal control strategy was presented for the single-phase cascade H-bridge(CHB)rectifier，serving as the input stage of the power electronic traction transformer，for its nonlinear and disturbed operating conditions.According to the nonlinear affine model of CHB and nonlinear differential geometric theory，the zero-dynamic control scheme based on partial feedback linearization was preferred.For the linear part，the feedback gain was optimized using the linear quadratic control method，and a resonant controller was added for achieving zero phase error tracking.For the zero-dynamic variable，the active disturbance rejection controller(ADRC)based on extended state observer was designed to improve its dynamic response under wide range of load disturbance.Experimental results show that the proposed control strategy has good performance in improving dynamic response under grid voltage and load disturbances，guaranteeing fast regulation and stability of grid current and dc voltage，meanwhile achieving unity power factor operation and dc voltage balance of each module.

Single-phase cascade H-bridge(CHB)，static coordinate，state feedback，zero-dynamic，active disturbance rejection controller(ADRC)

国家科技支撑计划(2013BAG24B02)和中央高校基本科研业务费专项资金(2015XS112)资助项目。

2016-08-20 改稿日期2016-12-21

TM464

孙玉巍 女，1987年生，博士研究生，研究方向为电力电子技术在电力系统中的应用和电力电子变压器。

E-mail：sunyuwei@ncepu.edu.cn(通信作者)

刘教民 男，1958年生，教授，博士生导师，研究方向为新能源电力系统特性与多源互补等。

E-mail：ljm6667@126.com