充电模态下电动汽车动力电池模型辨识

刘伟龙 王丽芳 廖承林 王立业

(1.中国科学院电力电子与电力传动重点实验室(电工研究所) 北京 100190 2.中国科学院大学 北京 100049)



充电模态下电动汽车动力电池模型辨识

刘伟龙1,2王丽芳1廖承林1王立业1

(1.中国科学院电力电子与电力传动重点实验室(电工研究所) 北京 100190 2.中国科学院大学 北京 100049)

电池模型及参数辨识是电动汽车动力电池进行充、放电优化控制的基础，同时模型参数受充、放电工况的影响。为对充电模态下的电动汽车动力电池进行建模与参数辨识，对动力电池建模方法、模型参数辨识算法展开研究，建立基于电极阻抗谱理论的可变阶次电池等效电路模型，提出基于遗忘因子扩展递推最小二乘算法(FFRELS)的模型参数辨识算法，构建基于贝叶斯信息准则(BIC)的电池模型最优阶次选择算法，创建基于晶格气体模型(LGM)的电池开路电压模型，对电池模型参数辨识算法进行修正，实现了充电模态下的电池模型参数辨识与最优阶次选择。仿真结果证明了该方法的有效性。

电池模型 参数辨识 遗忘因子 贝叶斯信息准则 晶格气体模型

0 引言

电动汽车使用电能代替燃油，是解决能源危机与环境问题的重要手段。目前，电动汽车作为汽车产业的发展方向已经成为普遍共识。动力电池是电动汽车的主要能量来源，决定着电动汽车的续航里程、动力性能以及使用经济性等。由于锂离子电池具有能量密度高、工作电压窗口宽、循环寿命长和没有记忆效应的优点，已成为电动汽车动力电池的首要选择。电动汽车在使用过程中，动力电池有充、放电两种工作模态。因为相较于传统汽车，电动汽车的能量补给速度有很大劣势，所以动力电池充电成为制约电动汽车推广的关键因素[1]。而电池模型及参数辨识是动力电池进行充电优化控制的基础。因此，建立能够通过动力电池的输入(激励电流)输出(响应电压)信息估算电池内部状态的电池模型，并研究充电模态下的动力电池模型参数实时辨识方法具有重要意义。

目前，动力电池模型的研究主要分为三类：电化学机理模型[2,3]、经验模型[4-6]和等效电路模型[7,8]。其中，电化学机理模型通过电化学反应第一性原理，以偏微分方程描述电化学动力学过程，含有大量先验电化学参数，计算复杂，不具备通用性。经验模型是基于实验数据通过输入输出量的非线性关系来表征其外部特性，该模型依赖于实验数据，很难满足预测精度要求。等效电路模型是将电池等效为集总参数电路，具有便于分析应用、通用性好的优点，取得了广泛应用。

在电池模型参数辨识方面，须基于一定的电池测试方法才能对电池模型参数进行辨识，现有的电池测试方法主要有两种：基于电动汽车运行工况得到的电池电流-时间曲线[9]；基于统计学分析设计的电池电流-时间曲线[10]。当电池模型参数辨识方法应用于充电模态下的动力电池参数辨识时，却有其局限性。常规充电模态主要有恒压充电、恒流充电和恒流-恒压充电。在常规充电模态下，电池的动态特性并不能得到充分激发，因此，电池模型参数辨识方法应用于充电模态时，并不能得到足够精确的模型参数，需进一步对此结论进行验证。综上，本文从充电模态下电池模型参数辨识的角度，对电池模型建立与模型参数辨识方法展开研究。

1 锂离子动力电池模型

建立电池模型是进行电池状态观测与优化控制的基础[11-13]。电池在充、放电的过程中，内部状态主要有欧姆极化、浓差极化和电化学极化[14]。典型的电池电路模型有Rint模型、Thevenin模型和DP模型等[15,16]。但这些模型的参数与电池内部状态并不具备一一对应的关系。基于电极阻抗谱理论[17]，建立的电池电路模型如图 1所示。图1中：Uoc为电池开路电压；Rs为电池等效内阻，与电池欧姆极化对应；Cdl为双电层电容，与电池浓差极化对应；ZF为电化学阻抗，与电池电化学极化对应；Rt为电荷转移电阻；n为模型阶次，n=0,1,2,…；nRC对应于电化学极化迟滞效应，RC数量越多，电池模型的精度越高，运算越复杂；Ut为电池端电压；iL为电池电流，充电为正，放电为负。下面对电池模型进行离散化处理，以便于应用参数辨识算法对电池模型参数进行辨识。

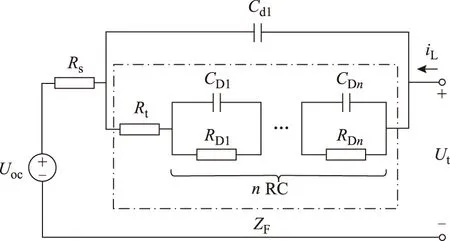
图1 锂离子动力电池电路模型结构Fig.1 Schematic of the lithium-ion power battery circuit model

首先，由基尔霍夫电压定律得到动力电池模型输出电压与输入电流的复频域数学关系表达式为

(1)

式中

(2)

其次，利用双线性变换法，将电池模型复频域式(1)从s平面映射到Z域，映射公式为

(3)

式中，Δt为系统的采样时间。将式(3)代入式(1)得电池模型Z域表达式为

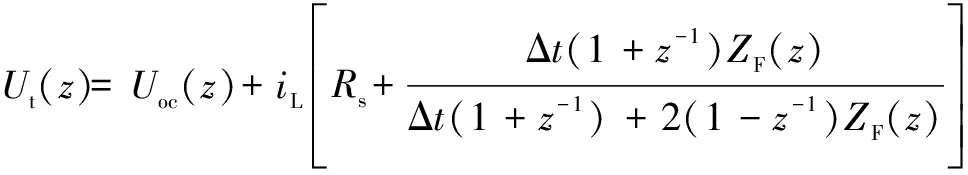
(4)

最后，因为动力电池开路电压Uoc与荷电状态(StateofCharge，SOC)、工作温度T、老化状态(State of Health，SOH)具有耦合关系，而通常情况下Δt非常小，所以在nΔt内假设SOC、T和SOH的变化均近似为0。因此，在nΔt内，电池开路电压Uoc变化近似为0，即

Uoc,k≈Uoc,k-1≈…≈Uoc,k-n

(5)

式中，k为采样时刻。对式(4)进行z逆变换，并将式(5)代入整理后，可得电池模型第k个采样时刻输出电压的时间域离散表达式为

an+1Ut,k-n-1+an+2iL,k+an+3iL,k-1+…+a2n+3iL,k-n-1

(6)

式中，ai为电池模型参数构成的待辨识参数，i=1,2,…,2n+3。

2 电池模型参数辨识方法

锂离子动力电池是一个参数时变的系统。本文锂离子动力电池模型参数辨识方法采用遗忘因子扩展递推最小二乘(ForgettingFactorRecursiveLeastSquare,FFRELS)算法，FFRELS结合遗忘因子递推最小二乘算法和递推扩展最小二乘(RecursiveExtendedLeastSquare,RELS)算法，继承了FFRLS和RELS算法的优点，可以解决因采集数据的增多出现的“数据饱和”问题，并且可以将每一次预测值相对测量值的偏差作为下一时刻的输入，进行迭代运算，提高了参数辨识的精度。

2.1FFRELS辨识算法

对于式(6)所示的电池输出表达式，可将其改写为矩阵相乘的形式，即

Ut,k=Φn,kθn,k

(7)

其中

Φn,k=[1,Ut,k-1,…,Ut,k-n-1,iL,k,…,iL,k-n-1]

(8)

θn,k=[a0,a1,…,a2n+3]T

(9)

(10)

式中，Φn,k为数据矩阵；θn,k为参数矩阵。

以yk表示电池电压的测量值，则电池系统方程可表示为

yk=Φn,kθn,k+ek

(11)

式中，ek为电池系统的有色噪声，其计算式为

ek=ξk+c1ξk-1+…+cncξk-nc

(12)

将ξk-i(i=1,…,nc)作为系统的输入置入系统数据矩阵，则电池系统方程可改写为

(13)

其中

(14)

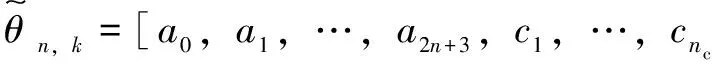
(15)

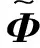
(16)

(17)

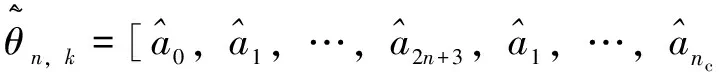
(18)

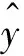
根据指数遗忘法，设定FFRELS的性能指标为

(19)

式中，λ为遗忘因子,0<λ≤1，本文取0.99；L为电池测试数据长度。使式(19)最小的电池系统参数矩阵为最优估计。该方法对测试数据施加了时变加权系数，最新的数据用1加权，而前面第n个采样周期的数据则用λn加权。为实现电池模型参数在线实时辨识，须将上述算法转换为递推算法，推导过程参考递推最小二乘算法[18]，得到FFRELS递推公式为

(20)

2.2 电池模型阶次选择

基于以上模型参数辨识算法，进行模型参数辨识，还须确定电池的模型阶次。电池模型阶次越高，模型对电池系统的输出预测精度就越高，但计算越复杂。因此，需要对电池模型阶次进行优化选择。

本文基于贝叶斯信息准则(BayesianInformationCriterions,BIC)选择最优模型阶次。BIC是考评综合最优配置的指标，为模型估计精度和模型参数数量的加权函数，是对赤池信息准则(AkaikeInformationCriterion,AIC)[19]的改进，考虑采集数据长度的影响。基于本文的电池模型，简化后的BIC为

(21)

式中，N为BIC采用的数据窗口宽度，N=10；p为电池模型参数数量，是模型阶次的函数，p=2n+3。式(21)右边第一项表示模型阶次对计算复杂度的影响，lnN为惩罚系数；右边第二项表示模型的预测精度。最小BIC值对应的模型阶次为最优阶次。

2.3 参数辨识算法与模型阶次选择实现

FFRELS算法的实现步骤为：

1)设置初始模型阶次n为0。

3)采样当前输出数据yk和输入数据iL,k。

6)数据更新迭代，时刻由k→k+1，返回步骤3，进行循环直至完成参数辨识计算。

7)BIC判定，根据式(21)计算BIC值，模型阶次加1，返回步骤2，重新进行循环，再次计算BIC值，直至得到不同阶次电池模型的BIC值，某一时刻最小BIC值对应的模型阶次即为这一时刻模型的最优阶次。

3 电池实验测试方法

本文选用双登50 A·h磷酸铁锂电池作为实验对象，电池参数见表 1。电池模型参数辨识算法是利用电池测试方法激发的电池动态特性来辨识模型参数，所以对电池测试方法的要求是能有效激发电池所有的动态特性，或者是能有效激发电池使用工况下的所有动态特性。传统的电池模型参数辨识实验测试方法通常是在放电模态下对电池进行测试，并不适用于动力电池充电模态下的模型参数辨识。常规动力电池充电方法中的恒流-恒压充电是目前应用最为广泛的充电方法。因此，本文采用恒流-恒压充电方法对实验电池进行充电测试，测试曲线如图 2所示。其中，恒流充电阶段采用恒流10 A充电，恒压充电阶段采用3.65 V进行充电，当恒压充电阶段充电电流小于0.5 A时，充电结束。为验证FFRELS算法的有效性和电池测试方法对电池模型参数辨识的影响，对电池进行了放电测试作为对比实验。放电测试实验采用由FUDS(federal urban driving schedule)工况对应的电池电流-时间曲线，如图 2所示。

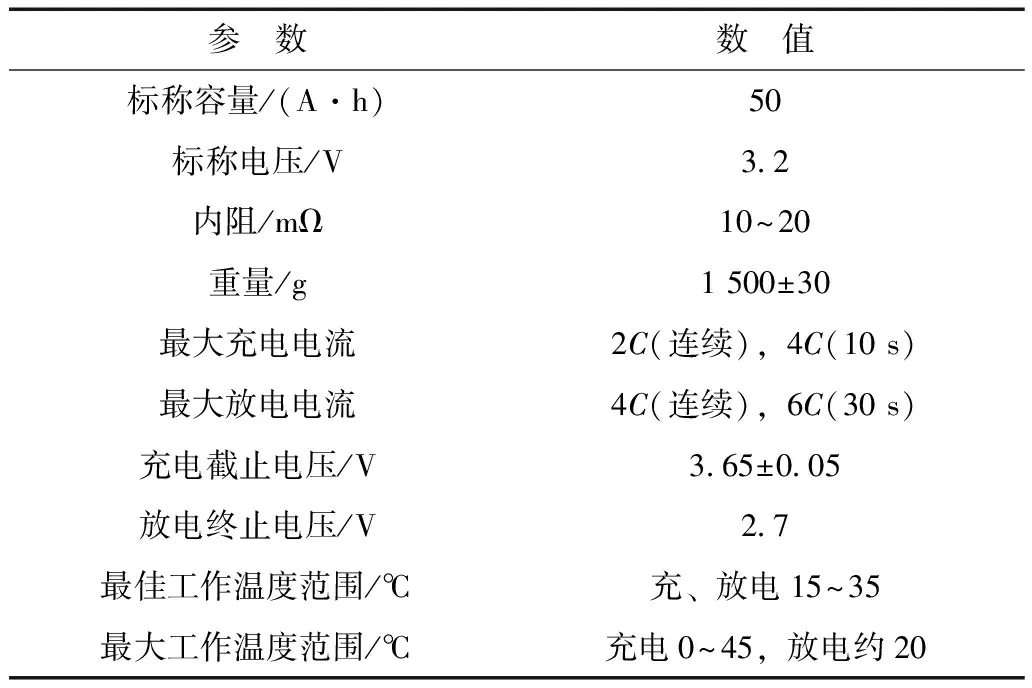
表1 磷酸铁锂动力电池技术规格

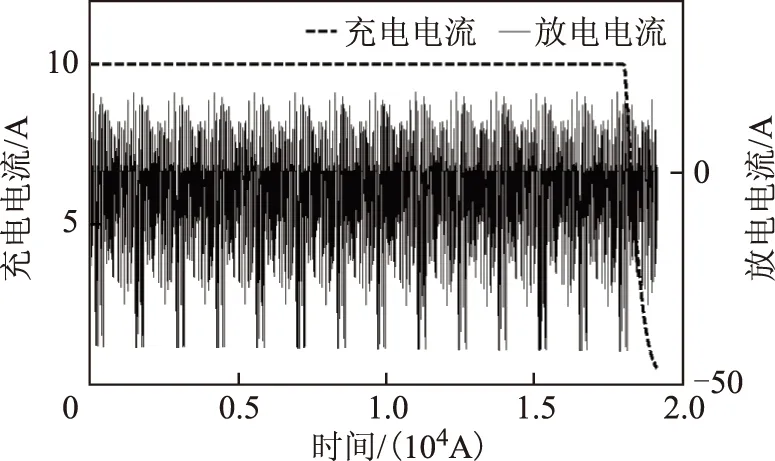
图2 动力电池充、放电测试曲线Fig.2 Charging and discharging test curves of the power battery

4 参数辨识方法验证与优化

基于上述锂离子动力电池模型与电池实验测试方法，对FFRELS进行验证。验证分为两方面：FFRELS有效性验证；测试工况对FFRELS的影响验证。其中，FFRELS有效性验证也包括两方面：算法估计电池端电压准确度验证;算法辨识模型参数有效性验证。对于算法估计电池端电压准确度的验证，通常采用实验电池标称电压的1%作为判断依据，即当最大辨识误差小于32 mV时，认为估计电压精度满足要求。对于算法辨识模型参数有效性的验证，电池模型参数中开路电压Uoc可测量得到，因此本文将其作为参数辨识有效性的判断依据。下面将基于电池0～5阶模型对参数辨识方法进行验证。

4.1 参数辨识方法的验证

首先，基于动力电池放电测试数据，验证FFRELS对电池端电压估计的准确度和放电测试工况对FFRELS算法的影响。基于不同阶次模型的FFRELS电池端电压估计误差如图 3所示，算法收敛后的估计误差始终小于11mV，小于电压估计准确度评判标准32mV，参数辨识结果初始误差较大，但算法能较快实现收敛。初始辨识误差大的原因是电池模型参数初始设置值与真实值之间存在较大差异。由图 3局部放大图可以看出，不同阶次模型的电压估计误差呈现规律近似的波动特性，对照图 2中的放电工况，可以看出放电工况的剧烈变化影响参数辨识算法的电压估计误差。不同阶次模型对应的BIC值如图 4所示，不同阶次模型的BIC值随时间呈现一定的波动特性，由局部放大图可以看出并不存在始终最优的模型阶次。FFRELS对不同阶次模型的电压估计误差分析见表 2，不同阶次模型的电压估计误差平均值均小于1mV，而电压估计误差最大值均小于80mV，这是因为FFRELS尚未收敛导致。由分析可知，在放电模态下FFRELS收敛后对电池模型电压估计准确度有效，放电工况影响FFRELS的电压估计误差，并且不同阶次模型的BIC值随放电工况呈现一定的波动特性，不存在始终最优的模型阶次。

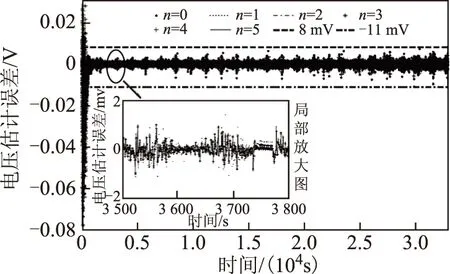
图3 放电模态不同阶次电池模型电压估计误差Fig.3 Voltage estimation deviations of different order battery models with discharging data

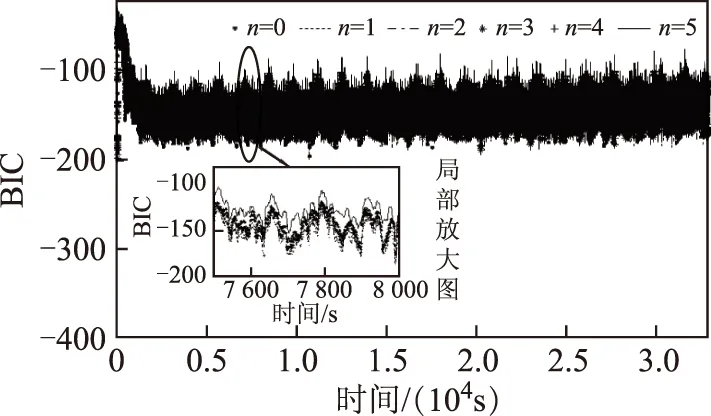
图4 放电模态不同阶次电池模型BIC值Fig.4 The BIC of different order battery models with discharging data

其次，基于动力电池充电测试数据，验证FFRELS对电池端电压估计的精准确度和充电测试工况对FFRELS的影响。不同阶次模型对应的电池端电压估计误差如图5所示，不同阶次模型电池端电压估计误差始终小于10mV，小于电压估计准确度评判标准32mV，FFRELS实现了快速收敛，但是FFRELS电压估计误差存在大量奇异值。由图 5局部放大图可以看出，不同阶次模型的端电压估计误差呈现规律近似的波动特性，对比图 3局部放大图可知,平稳的充电测试工况带来电池端电压估计误差的平稳波动特性，剧烈变化的放电测试工况导致电池端电压估计误差的剧烈波动。充电模态下不同阶次模型对应的BIC值如图 6所示，可以看出充电模态下不同阶次模型的BIC值同样存在波动特性，由局部放大图可以看出，不存在始终最优的模型阶次。不同阶次模型的FFRELS电压估计误差分析见表 3，可知FFRELS对不同阶次模型输出电压的平均估计误差均小于0.05 mV，最大电压估计误差均小于10 mV。对比图 3和图 5可知，FFRELS在充电测试工况下可以更快地实现收敛。因此，FFRELS在电池充电模态下对电池端电压估计的准确度有效，并且与放电模态相比拥有更高的估计精度，电池的充放电测试工况影响电池端电压估计误差，不同模型阶次的BIC值随充电工况呈现一定的波动特性，不存在始终最优的模型阶次。

表2 放电模态下不同阶次模型电压估计误差分析

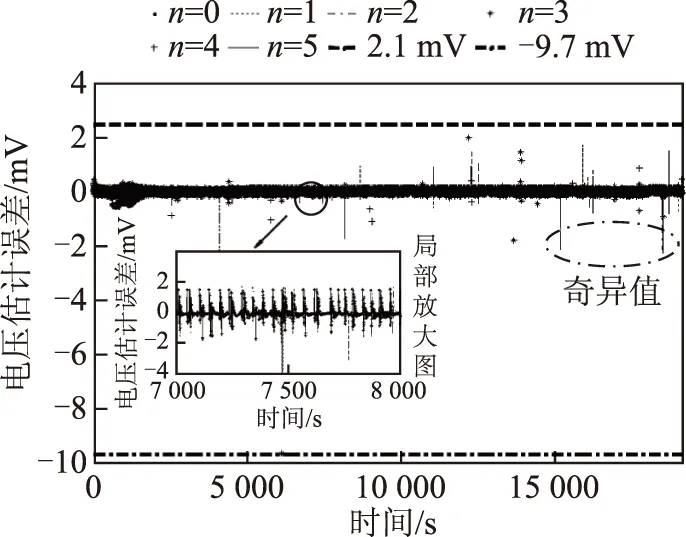
图5 充电模态不同阶次电池模型电压估计误差Fig.5 Voltage estimation deviations of different order battery models with charging data

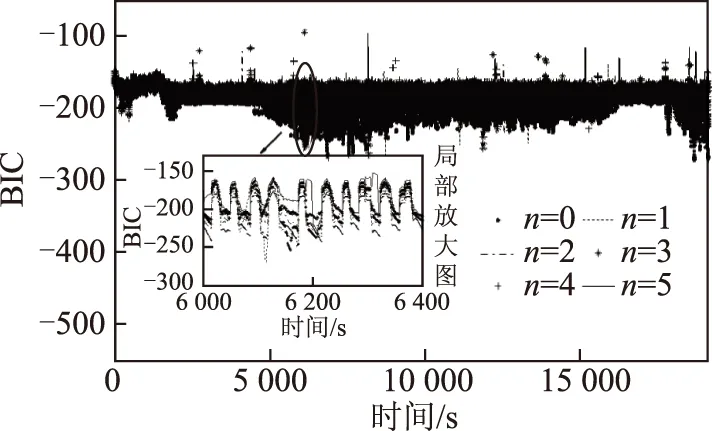
图6 充电模态不同阶次电池模型BIC值Fig.6 The BIC of different order battery models with charging data

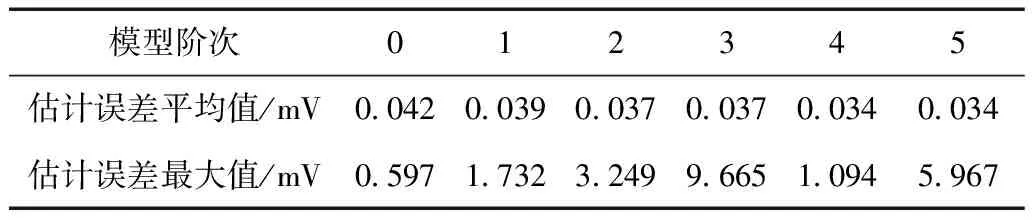
模型阶次012345估计误差平均值/mV0 0420 0390 0370 0370 0340 034估计误差最大值/mV0 5971 7323 2499 6651 0945 967

最后，基于动力电池的放电和充电测试数据，验证FFRELS辨识模型参数的有效性。对电池0～5阶模型，采用FFRELS分别辨识电池充、放电模态下的开路电压，结果如图7所示。本文实验用的动力电池的开路电压范围在2.7～3.5 V之间，并且由上文假设在采样时间Δt内，SOC变化近似为0，根据电池开路电压与SOC的对应关系可知，在某个测试点附近电池开路电压应基本保持不变。但是由图7a所示放电模态下开路电压的估计值在大部分测试时间内远小于2.7V，图7b所示充电模态下开路电压估计值存在大量-400～100V之间的奇异值，并且从图7a、图7b局部放大图看，开路电压估计值波动剧烈。因此，可知FFRELS对电池开路电压辨识结果是不准确的。这是因为辨识的电池模型参数表示的是电池测试曲线所激发的电池动态特性，并不能反映电池的本征特性，所以不同测试工况将影响电池模型参数的准确辨识。同时，由于FFRELS在充电模态下对电池模型参数的辨识结果产生了奇异值，这也影响电池模型参数的求解，因此在充电模态下电池开路电压的估计值也产生了大量奇异值。

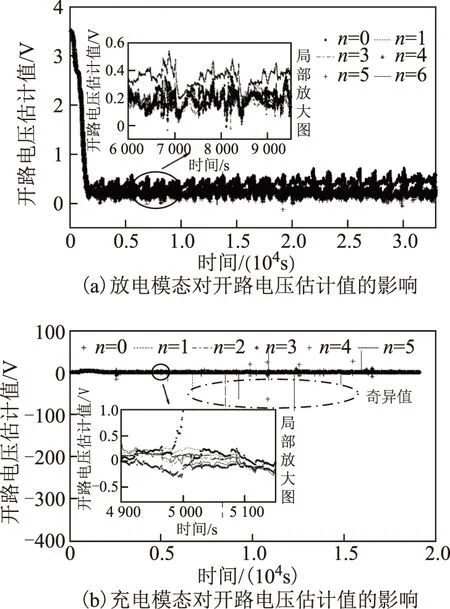
图7 充、放电模态对动力电池开路电压估计值的影响Fig.7 The influence of charging and discharging mode to the power battery′s open circuit voltage estimations

综上分析，不论FFRELS在电池放电模态下还是充电模态下，都可以对电池端电压进行有效地估计，但是电池测试工况会对FFRELS的电压估计精度、算法收敛速度和电池模型参数估计造成影响。即基于测试数据辨识得到的电池模型，具有与测试电池相同的输出特性，但电池模型参数却并不能表征电池的内部状态，此时的电池模型参数只与电池测试方法相关。因此，要辨识得到电池模型的准确参数，就必须对辨识算法进行优化改进。

4.2 参数辨识算法的优化

参数辨识算法的修正可以从两个方面进行考虑：①设 计可以激发动力电池全部动态特性的电池测试方法；②从修正电池部分状态参量估计值的角度对参数辨识算法进行改进，即对动力电池的开路电压估计值进行实时修正，从而实现对电池其他状态参量的精确估计。

对于前者，很难设计可以完全激发电池动态特性的测试曲线。同时，电池在充电模态下进行参数辨识，可供选择的充电方法有限。因此，采用开路电压修正的参数辨识算法是较为可行的方案。

电池的开路电压通常采用多项式进行拟合，而此种方式拟合的结果并不理想。因此本文采用基于晶格气体模型[20](LatticeGasModel，LGM)的锂离子动力电池开路电压模型来描述锂离子动力电池开路电压。对于晶体嵌入材料，因LGM考虑了离子电势、嵌入离子熵值、离子相互作用对电势的影响和嵌入电子电势，在计算电池电动势领域得到了成功的应用。LGM的表达式为

(22)

式中，U为电极电势；E0为离子电势；k为玻耳兹曼常数；T为热力学温度；xr为晶格中离子的占有率；Wxr为离子间相互作用对电势的影响；Vel为嵌入电子电势。

基于LGM的锂离子动力电池开路电压模型为

Uoc=a+bz+cz2+dz3+ez4+fz5+gz6+hz7+

(23)

式中，a、b、c、d、e、f、g、h、i、j、l、m、n、p、q为模型拟合参数；z为电池的SOC值，具体推导过程见附录。电池开路电压数据采用充、放电5A·h静置2h取平均值的方法得到，并使用最小二乘法进行曲线拟合，拟合曲线如图 8所示。需要说明的是，本文采用电池SOC的定义为电池可用于充、放电的容量与电池标称容量之比。由于本文测试电池的充、放电容量大于标称容量，所以此电池充满电时SOC大于1。

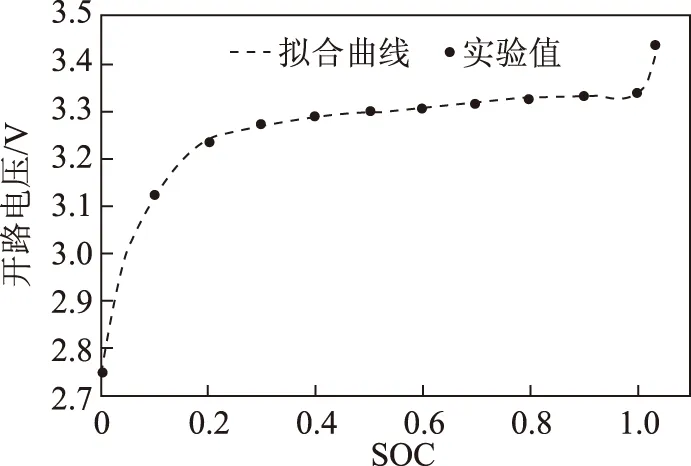
图8 开路电压拟合曲线Fig.8 The fitting curve of open circuit voltage

采用LGM开路电压模型修正的FFRELS流程如图 9所示，其中，Ek为电池的极化电压，包括欧姆极化电压、浓差极化电压和电化学极化电压，Ek=yk-Uoc,k。基于动力电池的充电测试数据，使用修正的FFRELS对动力电池0～5阶模型进行参数辨识。不同模型阶次对应的电池端电压估计误差如图 10所示，不同阶次模型输出电压最大估计误差不超过0.4mV，相比算法修正前有明显的改善，远小于电压估计精确度评判标准32mV，并且算法不存在电压估计奇异值，可实现快速收敛。不同阶次模型参数辨识算法估计值分析见表 4，不同阶次模型输出电压的平均估计误差均小于0.04mV，相比算法修正前电压估计精度也有提高。

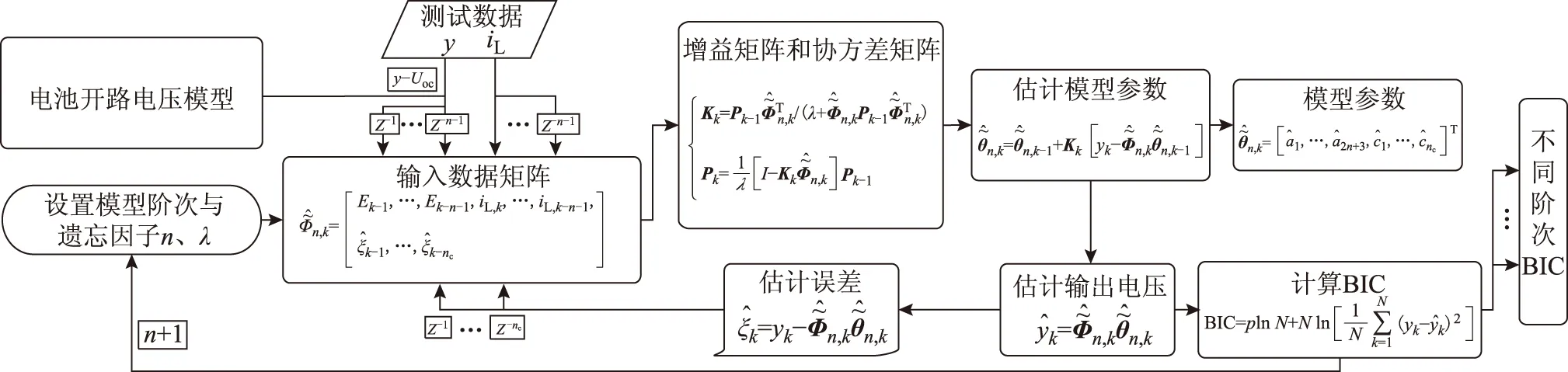
图9 LGM开路电压模型修正的FFRELS算法流程Fig.9 The amended FFRELS algorithm with the LGM open circuit voltage model

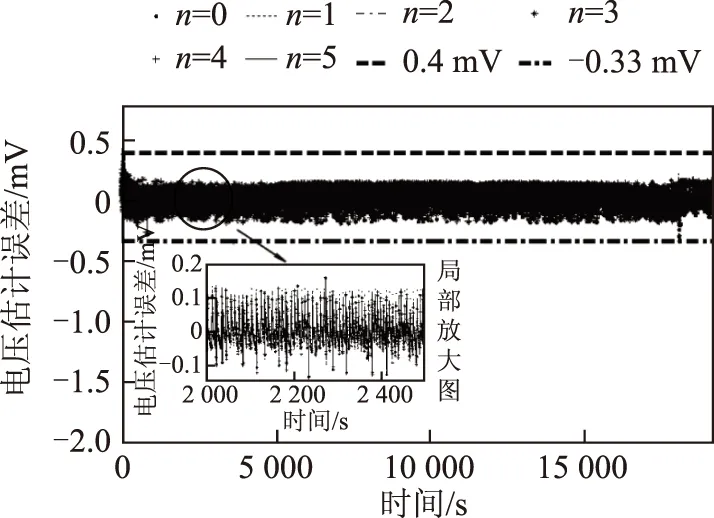
图10 充电模态修正的模型电压估计误差Fig.10 Amended voltage estimated deviations of different order battery models with charging data

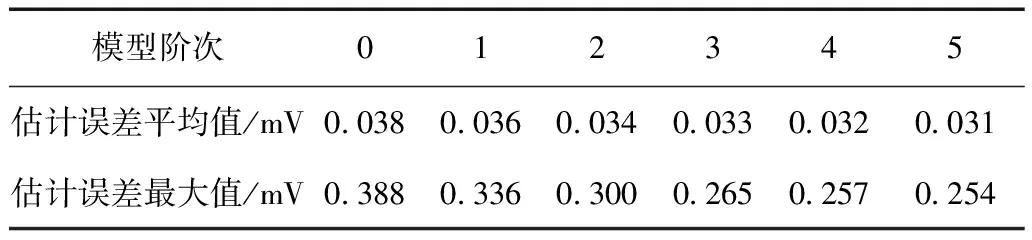
模型阶次012345估计误差平均值/mV0 0380 0360 0340 0330 0320 031估计误差最大值/mV0 3880 3360 3000 2650 2570 254

修正的FFRELS对动力电池0～5阶模型辨识的BIC值如图 11所示，由图可看出修正算法对不同阶次

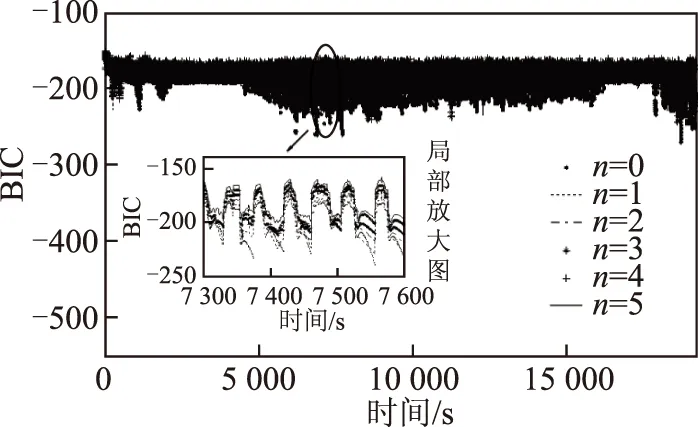
图11 充电模态下修正的模型BIC值Fig.11 The amended BIC with charging data

模型的BIC值也存在一定的波动状态，由局部放大图可以看出不存在始终最优的模型阶次。最小的BIC值对应的最优模型阶次的时间与整个充电过程时间之比用饼状图 12表示，可以看出0和1阶次作为电池模型最优阶次的时间占比99%，为电池模型主要的最优阶次，考虑到修正FFRELS对动力电池0～5阶模型的电压估计始终满足精确度评判标准，可认为在本文测试充电模态下，电池模型的最优阶次可通过BIC在0和1之间选取。

修正的FFRELS对电池开路电压估计值及估计误差如图13所示，由于对FFRELS采用LGM开路电压模型进行了修正，所以电池开路电压估计误差与电池端电压估计误差相等；并且电池测试方法不再对电池的开路电压辨识造成影响，而是对电池模型极化参数产生作用，因此修正的FFRELS辨识得到的是与电池测试方法相关的电池极化参数，可以表征电池在特定测试方法下的内部极化状态。同时，该修正的FFRELS也适用于电池放电模态下的模型参数辨识，限于本文篇幅，在此不进行讨论。

图12 最优模型阶次时间占比饼状图Fig.12 The pie chart of optimal battery model′s time ratio

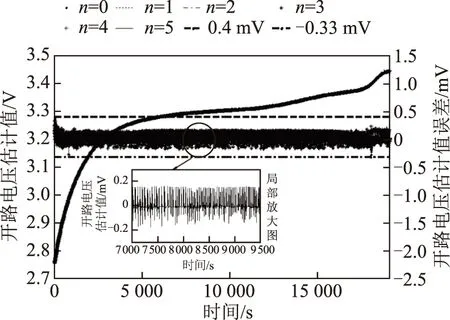
图13 充电模态下修正的模型开路电压估计值及误差Fig.13 Amended open circuit voltage and estimated deviations with charging data

5 结论

本文围绕充电模态下电动汽车动力电池模型辨识这一核心问题，提出基于FFRELS的参数辨识算法，建立基于电极电化学阻抗谱理论的电池电路模型，并进行模型参数辨识研究，采用BIC准则对电池模型阶次进行优化选择，并使用基于LGM的电池开路电压模型对参数辨识算法FFRELS进行修正。

通过对模型参数辨识算法的验证表明，FFRELS满足动力电池模型输出电压精度的评判标准，并且不依赖于电池的工作模态与测试工况，但辨识得到的动力电池模型参数有效性与电池工作模态和测试工况相关。针对充电工况选择有限的问题，采用基于LGM的电池开路电压模型对FFRELS进行修正，修正的FFRELS可以避免测试工况对电池开路电压参数辨识的影响，辨识得到的动力电池模型参数可以反映该测试工况下的电池极化特性，修正的FFRELS对电池端电压及开路电压的平均估计误差小于0.04 mV，最大估计误差小于0.4 mV，可以很好地满足电动汽车的使用需求。

通过BIC计算表明，不同阶次动力电池模型的BIC值呈现波动特性，不存在始终最优的模型阶次。通过对不同阶次模型BIC值分析得到0和1为本文恒流-恒压充电模态下动力电池模型的主要最优阶次，在满足电压估计精度评判标准的前提下，通过BIC可在0和1之间选择动力电池模型最优阶次。由于本文提出的电池模型及参数辨识算法并不依赖于本文使用的锂离子电池，因此具有较好的普遍适用性。

附录 锂离子动力电池开路电压模型

锂离子动力电池由正、负两电极组成，因此开路电压可表示为

Uoc=U+-U-

(A1)

式中，U+为正极电势；U-为负极电势。

在锂离子动力电池充、放电循环过程中，为保护电极材料晶体结构，须防止电极材料中锂离子过度脱嵌[21]，即电极材料中有部分锂离子并不参与充、放电。因此正、负极材料晶格中锂离子的占有率可以表示为

(A2)

式中，C+、C-分别为正、负电极内锂离子数；Cm+、Cm-分别为正、负电极内锂离子最大数；Czm+、Czm-分别为正、负电极内参与一次充电或放电的锂离子最大数，Czm+=Czm-=Czm；Cz+、Cz-分别为当前正、负电极材料内可用于充电或放电的锂离子数，Cz++Cz-=Czm；C0+、C0-分别为正、负电极不用于充电或放电的锂离子数，且均大于零。电池的标称容量对应的锂离子数用C表示，正、负极材料晶格中锂离子的占有率可改写为

(A3)

式中，Cz-/C为电池的荷电状态，即SOC；Czm/C为电池真实容量与标称容量之比，用1+r′替代；C0+/C表示电池正极不参与充放电的容量与标称容量之比，用p′代替；C0-/C为电池负极不参与充放电的容量与标称容量之比，用n代替。则正、负极材料晶格中锂离子的占有率可改写为

(A4)

将式(A4)代入式(22)可得

(A5)

将式(A5)代入式(A1)得

Uoc=E0+-E0--(Wxr+-Wxr+)+Vel+-Vel-+

(A6)

式中，E0+-E0--(Wxr+-Wxr+)+Vel+-Vel-与电池的荷电状态z相关，本文采用多项式拟合的方式得到，因此式(A6)可改写为

Uoc=a+bSOC+cSOC2+dSOC3+eSOC4+fSOC5+gSOC6+

(A7)

LGM模型描述的是理想晶格材料的电势特性，并在xr等于0或1时模型失效。根据上文讨论，因C0+、C0-均大于零，所以由式(A2)可知xr>0。为提高模型适用性并解决xr=1模型失效的问题，采用拟合参数j、l代替式(A7)中的参数kT和增加拟合参数m的方法，则

Uoc=a+bSOC+cSOC2+dSOC3+eSOC4+fSOC5+gSOC6+

(A8)

令r′+p′=p、r′+m=q，满足m>0，且1+q大于电池充满电时SOC，可得锂离子动力电池开路电压模型为

Uoc=a+bSOC+cSOC2+dSOC3+eSOC4+fSOC5+gSOC6+

(A9)

[1] 党杰, 汤奕, 宁佳, 等. 基于用户意愿和出行规律的电动汽车充电负荷分配策略[J]. 电力系统保护与控制, 2015, 43(16): 8-15.DangJie,TangYi,NingJia,etal.Astrategyfordistributionofelectricvehicleschargingloadbasedonuserintentionandtriprule[J].PowerSystemProtectionandControl, 2015, 43(16): 8-15.

[2]SmithKA,RahnCD,WangCY.ControlorientedIDelectrochemicalmodeloflithium-ionbattery[J].EnergyConversionandManagement, 2007, 48(9): 2565-2578.

[3]SmithKA,RahnCD,WangCY.Model-basedelectrochemicalestimationandconstraintmanagementforpulseoperationoflithium-ionbatteries[J].IEEETransactionsonControlSystemsTechnology, 2010, 18(3): 654-663.

[4]ShenWX,ChanCC,LoEWC,etal.Anewbatteryavailablecapacityindicatorforelectricvehiclesusingneuralnetwork[J].EnergyConversionandManagement, 2002, 43(6): 817-826.

[5]ChauKT,WuKC,ChanCC.Anewbatterycapacityindicatorforlithium-ionbatterypoweredelectricvehiclesusingadaptiveneuro-fuzzyinferencesystem[J].EnergyConversionandManagement, 2004, 45(11-12): 1681-1692.

[6] 孙丙香, 高科, 姜久春, 等. 基于ANFIS和减法聚类的动力电池放电峰值功率预测[J]. 电工技术学报, 2015, 30(4): 272-280.SunBingxiang,GaoKe,JiangJiuchun,etal.ResearchondischargepeakpowerpredictionofbatterybasedonANFISandsubtractionclustering[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(4): 272-280.

[7]WaagW,FleischerC,SauerDU.On-lineestimationoflithium-ionbatteryimpedanceparametersusinganovelvaried-parametersapproach[J].JournalofPowerSources, 2013, 237(3): 260-269.

[8]WaagW,SauerDU.Adaptiveestimationoftheelectromotiveforceofthelithium-ionbatteryaftercurrentinterruptionforanaccuratestate-of-chargeandcapacitydetermination[J].AppliedEnergy, 2013, 111(4): 416-427.

[9]HeHongwen,XiongRui,GuoHongqiang.Onlineestimationofmodelparametersandstate-of-chargeofLiFePO4batteriesinelectricvehicles[J].AppliedEnergy, 2012, 89(1): 413-420.

[10]李勇, 王丽芳, 廖承林, 等. 基于子空间技术的电动汽车电池模型辨识研究[J]. 电工电能新技术, 2015, 34(1): 1-6.LiYong,WangLifang,LiaoChenglin,etal.Researchonsubspace-basedidentificationofbatterymodelforelectricvehicles[J].AdvancedTechnologyofElectricalEngineeringandEnergy, 2015, 34(1): 1-6.

[11]程泽, 董梦男, 杨添剀, 等. 基于自适应混沌粒子群算法的光伏电池模型参数辨识[J]. 电工技术学报, 2014, 29(9): 245-252.ChengZe,DongMengnan,YangTiankai,etal.Extractionofsolarcellmodelparametersbasedonself-adaptivechaosparticleswarmoptimizationalgorithm[J].TransactionsofChinaElectrotechnicalSociety, 2014, 29(9): 245-252.

[12]冯飞, 宋凯, 逯仁贵, 等. 磷酸铁锂电池组均衡控制策略及荷电状态估计算法[J]. 电工技术学报, 2015, 30(1): 22-29.FengFei,SongKai,LuRengui,etal.EqualizationcontrolstrategyandSOCestimationforLiFePO4batterypack[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(1): 22-29.

[13]冯飞, 逯仁贵, 朱春波. 一种锂离子电池低温SOC估计算法[J]. 电工技术学报, 2014, 29(7): 53-58.FengFei,LuRengui,ZhuChunbo.StateofchargeestimationofLi-ionbatteryatlowtemperature[J].TransactionsofChinaElectrotechnicalSociety, 2014, 29(7): 53-58.

[14]MitsudaK,TakemuraD.Polarizationstudyofalithium-ionbatterywithanextrapositiveelectrodeusingeightreferenceelectrodes[J].Electrochemistry, 2008, 76(12): 880-885.

[15]HeHongwen,XiongRui,GuoHongqiang,etal.Comparisonstudyonthebatterymodelsusedfortheenergymanagementofbatteriesinelectricvehicles[J].EnergyConversionandManagement, 2012, 64(4): 113-121.

[16]刘艳莉, 戴胜, 程泽, 等. 基于有限差分扩展卡尔曼滤波的锂离子电池SOC估计[J]. 电工技术学报, 2014, 29(1): 221-228.LiuYanli,DaiSheng,ChengZe,etal.Estimationofstateofchargeoflithium-ionbatterybasedonfinitedifferenceextendedkalmanfilter[J].TransactionsofChinaElectrotechnicalSociety, 2014, 29(1): 221-228.

[17]HuetF.Areviewofimpedancemeasurementsfordeterminationofthestate-of-chargeorstate-of-healthofsecondarybatteries[J].JournalofPowerSources, 1998, 70(1): 59-69.

[18]庞中华, 崔红. 系统辨识与自适应控制MATLAB仿真[M]. 北京: 北京航空航天大学出版社, 2013.

[19]商云龙, 张奇, 崔纳新, 等. 基于AIC准则的锂离子电池变阶RC等效电路模型研究[J]. 电工技术学报, 2015, 30(17): 55-62.ShangYunlong,ZhangQi,CuiNaxin,etal.Researchonvariable-orderRCequivalentcircuitmodelforlithium-ionbatterybasedontheAICcriterion[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(17): 55-62.

[20]KalikmanovVI,KoudriachovaMV,deLeeuwSW.Lattice-gasmodelforintercalationcompounds[J].SolidStateIonics, 2000, 136(11): 1373-1378.

[21]IslamMS,FisherCAJ.Lithiumandsodiumbatterycathodematerials:computationalinsightsintovoltage,diffusionandnanostructuralproperties[J].ChemicalSocietyReviews, 2014, 43(1): 185-204.

(编辑 张洪霞)

Parameters Identification Method of Battery Model for Electric Vehicles under the Charging Mode

LiuWeilong1,2WangLifang1LiaoChenglin1WangLiye1

(1.Key Laboratory of Power Electronics and Electric Drives Institute of Electrical Engineering Chinese Academy of Science Beijing 100190 China 2. University of Chinese Academy of Sciences Beijing 100049 China)

The battery model and parameters identification are the base of the charge and discharge optimal control of electric vehicle traction batteries. And the parameters of the battery model are affected by the working condition of the traction battery. In order to model the traction battery and identify the model parameters, modeling algorithm of traction battery and parameters identification method were studied in this paper. A variable order equivalent circuit model was established, which is based on the electrode impedance spectrum theory. A parameter identification algorithm was proposed, which is based on the forgetting factor recursive extended least square (FFRELS). A selection algorithm for the optimal order of the battery model was built, which is based on the Bayesian information criterions (BIC). A battery open circuit voltage model that was used for calibration of the proposed parameter identification algorithm was created, which is based on the lattice gas model (LGM). In the end, the battery model parameters identification algorithm and the optimal order selection under the charging mode was achieved. Validation results show that the proposed modeling and parameters identification algorithm is efficient.

Battery model, parameters identification, forgetting factor, Bayesian information criterions, lattice gas model

国家重点研发计划项目(2016YFB0101801,2016YFB0101800)和国家电网公司科技项目“电动汽车基础设施运行安全与互联网互通技术”资助。

2016-03-05 改稿日期2017-01-04

TM912.8

刘伟龙 男，1988年生，博士研究生，研究方向为电动汽车电池管理技术。

E-mail：liuweilong@mail.iee.ac.cn(通信作者)

王丽芳 女，1971年生，博士，研究员，研究方向为电动汽车电池管理技术和电动汽车无线充电技术等。

E-mail：wlf@mail.iee.ac.cn