浅埋黄土地铁双连拱隧道施工引起地表沉降特征研究

刘新军

(中铁第一勘察设计集团有限公司,710043,西安∥高级工程师)



浅埋黄土地铁双连拱隧道施工引起地表沉降特征研究

刘新军

(中铁第一勘察设计集团有限公司,710043,西安∥高级工程师)

以西安地铁4号线飞天路站到航天大道站区间双连拱隧道工程为例,通过FLAC3D软件模拟计算隧道两侧洞室采用CRD法(交叉中隔墙法)施工时各阶段地表沉降,并与现场监测数据进行对比。结果表明：两侧洞室施工引起地表沉降占总沉降的65%,上导洞施工引起地表沉降占该阶段总沉降的67%；控制上导洞施工引起的沉降是控制最终沉降的关键。中洞施工时,在监测断面前后1.5倍单个导洞宽度范围内地表沉降增长速率较大;两侧洞室施工时,在监测断面前后5倍单个导洞宽度范围内地表沉降增长速率较大。当施工到该范围内时,应及时进行初期支护并加强监测。

双连拱隧道; 地表沉降; 数值模拟

Author′s address China Railway First Survey & Design Institute Group Co.,Ltd.,710043,Xi′an,China

在特殊地质及地形条件地区,为保证线路流畅,断面造型美观,可采用双连拱隧道。但连拱隧道跨度大,施工工序繁琐,围岩受扰动次数多,中墙受力复杂,结构体系转换频繁。为了全面了解连拱隧道在施工过程中围岩的稳定性、支护结构的受力演变以及地表变形规律,国内许多学者对双连拱隧道展开了一系列研究。胡庆安等[1]利用ANSYS软件对隧道围岩的变形进行了三维有限元分析,得出了右洞开挖对左洞围岩位移的影响约为开挖面前后3B(B为单洞开挖跨度)的范围。任安菊[2]对连拱隧道施工过程进行了三维弹塑性有限元数值模拟,得到了施工过程中围岩应力集中区分布情况,并分析了最终地表沉降曲线的特点。杨萌[3]对双连拱隧道的开挖及支护全过程进行有限元模拟,分析了不同工序下围岩和衬砌结构的应力和变形规律。许多学者还结合实际工程探讨了双连拱隧道的开挖技术[4-6]，并对中墙进行了空间力学效应分析[7-9]。但是,以上研究大多是进行了连拱隧道在开挖工程中围岩的应力场和位移场分析、衬砌结构应力和位移变化规律的探讨，以及中墙受力随开挖过程变化的情况,较少讨论黄土地铁连拱隧道左右侧洞室采用CRD法(交叉中隔墙法)施工时的地表沉降规律。本文依托西安地铁4号线飞天路站—航天大道站区间双连拱隧道工程,利用FLAC3D软件对隧道施工过程进行计算,分析地表变形特征,并与实测数据对比,其研究结果可为类似工程提供参考。

1 工程概况

西安地铁4号线飞天路站—航天大道站区间连拱隧道沿神州四路地下布设。神舟四路为城市主干路,两侧有住宅小区,道路宽度为50 m,为双向4车道沥青路面,道路车流量平时一般,上下班高峰期车流量较大。隧道起止里程为YZDK4+913.848～YDK5+127.430,隧道全长约214 m,整体跨度为22.41 m,高10.13 m,中洞采用正台阶法施工,在中洞施工完成之后施工中墙,最后采用CRD法施工左右两侧洞室。隧道断面如图1和图2所示,其中A点为道路中心点,L1为开挖步距,L2为台阶长度,L3为相邻导洞掌子面相差距离,L4为左右两侧相对应导洞掌子面相差距离。隧道采用复合式衬砌结构进行支护,支护参数见表1。采用超前小导管、超前大管棚进行预加固,小导管厚度t=3.5 mm,长度l=3.5 m,外插角θ=15°,钢管直径d=42 mm,环向间距为0.4 m,纵向间距为2.0 m。

该区段内湿陷性土层最大埋深为27.8 m,最大厚度为19.2 m,属于自重湿陷性黄土,湿陷性等级为Ⅱ。地下水位埋深46.5 m,其补给主要有大气降水、侧向径流及局部水管渗漏等,排泄方式主要为径向排泄、人工开采和潜水越流排泄等。

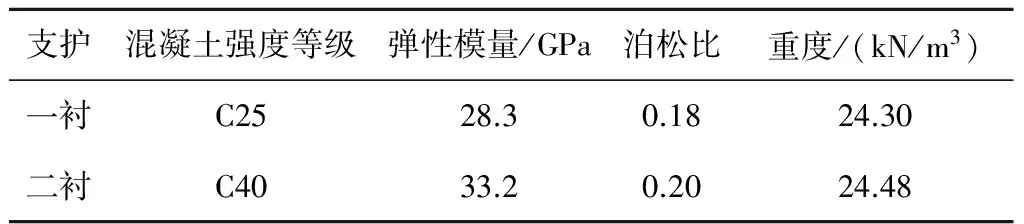
表1 支护参数表

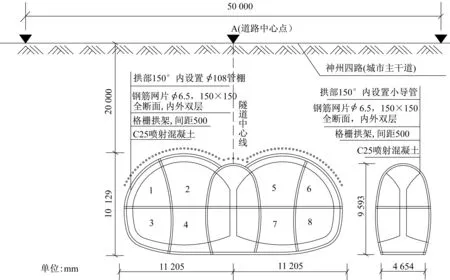
图1 隧道横向断面图

图2 隧道纵向断面图

2 数值模拟

2.1 计算模型

本文采用FLAC3D数值模拟软件建立了三维计算模型,岩土体采用实体单元模拟,其本构模型为Mohr-Coulomb,相应的材料参数与地质勘探资料相同。注浆区采用增大岩土体参数的方法来模拟。衬砌采用实体单元模拟,其本构模型为弹性各向同性模型。钢拱架的作用按照等效的方法予以考虑,即是将钢拱架的弹性模量折算给混凝土,其计算公式[10]为:

E=E0+

式中:

E——折算后混凝土弹性模量;

E0——折算前混凝土弹性模量;

Eg——钢材弹性模量;

Sg——钢拱架横截面积;

Sc——混凝土截面面积。

由于道路在高峰期时车流量较大,故在模拟过程中对地表施加附加荷载,附加荷载按照15 kPa考虑。考虑到隧道开挖对周围土体的影响范围,计算模型尺寸为X·Y·Z=120 m×48 m×72 m,模型共92 328个单元,98 700个节点。建立的CRD法施工模型如图3所示。

模型的边界条件为:左右两侧约束X方向位移,前后两侧约束Y方向位移,底面约束Z方向位移。

2.2 计算参数

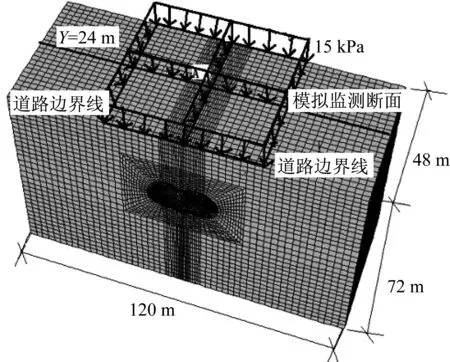
图3 CRD法计算模型

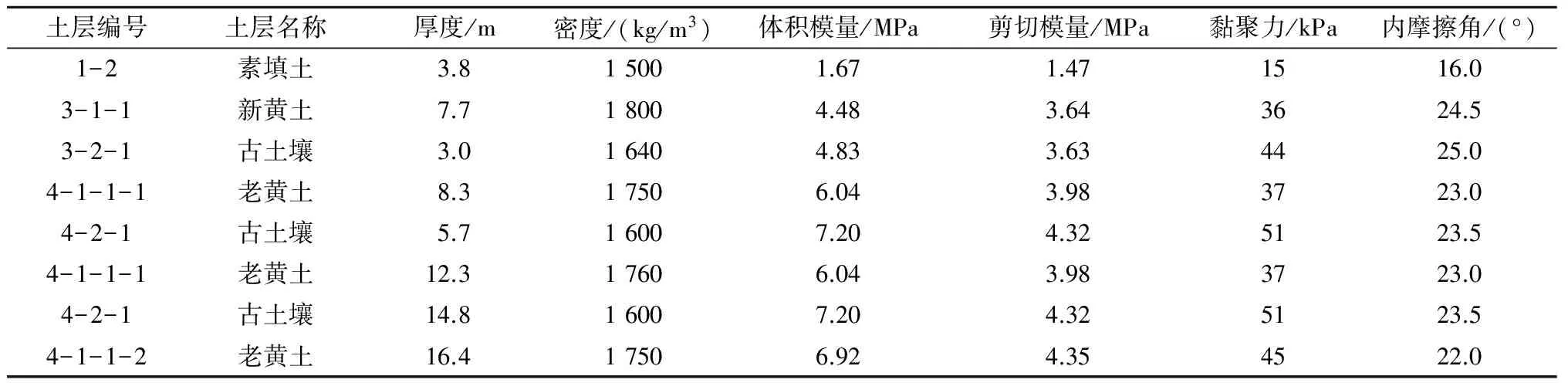
表2 土层物理力学性质指标

2.3 隧道开挖

模拟开挖过程中,开挖步距L1=0.5 m,台阶长度L2=4 m,相邻导洞掌子面相差L3=12 m,左右侧相对应导洞掌子面相差L4=12 m,对Y=24 m处的地表点进行监测。 施工步骤如表3所示。

表3 施工步骤

3 计算结果分析

3.1 地表沉降横向变化过程

各施工阶段引起的地表沉降见表4。由表可知:

(1) 中洞施工完成后,地表沉降最大值为11.02 mm,占总沉降的31%。上导洞开挖到监测断面时,由于施工扰动引起应力释放,地表沉降占该阶段总沉降的大部分,为64%,故在施工上导洞时可加强对围岩的预加固,并控制进尺和开挖速度来限制地层移动。当下导洞通过监测断面之后,由于衬砌变形、土体固结和混凝土失水收缩,引起的地表沉降占该阶段总沉降的20.16%,故要注意及时在背后注浆。

(2) 施工中墙时,中洞施工已完成且地表沉降基本稳定,故对其扰动很小,引起的地表沉降仅占总沉降的5%。

(3) 两侧导洞施工完成后,地表沉降最大值为34.58 mm,占总沉降的63.87%,两侧洞室上导洞开挖时,拱顶上方土体由于应力重分布必然向临空面移动,引起地表较大沉降,沉降量占该阶段总沉降的68%。下导洞开挖时,对土体扰动小,且上导洞已支护封闭成环,承担了一部分压力,故引起地表沉降较小,沉降量占该阶段总沉降的25.47%。后期由于衬砌变形、土体固结和混凝土收缩引起的地表沉降占总沉降的6.53%。故控制该阶段沉降的关键在于控制上导洞开挖引起的地表沉降。

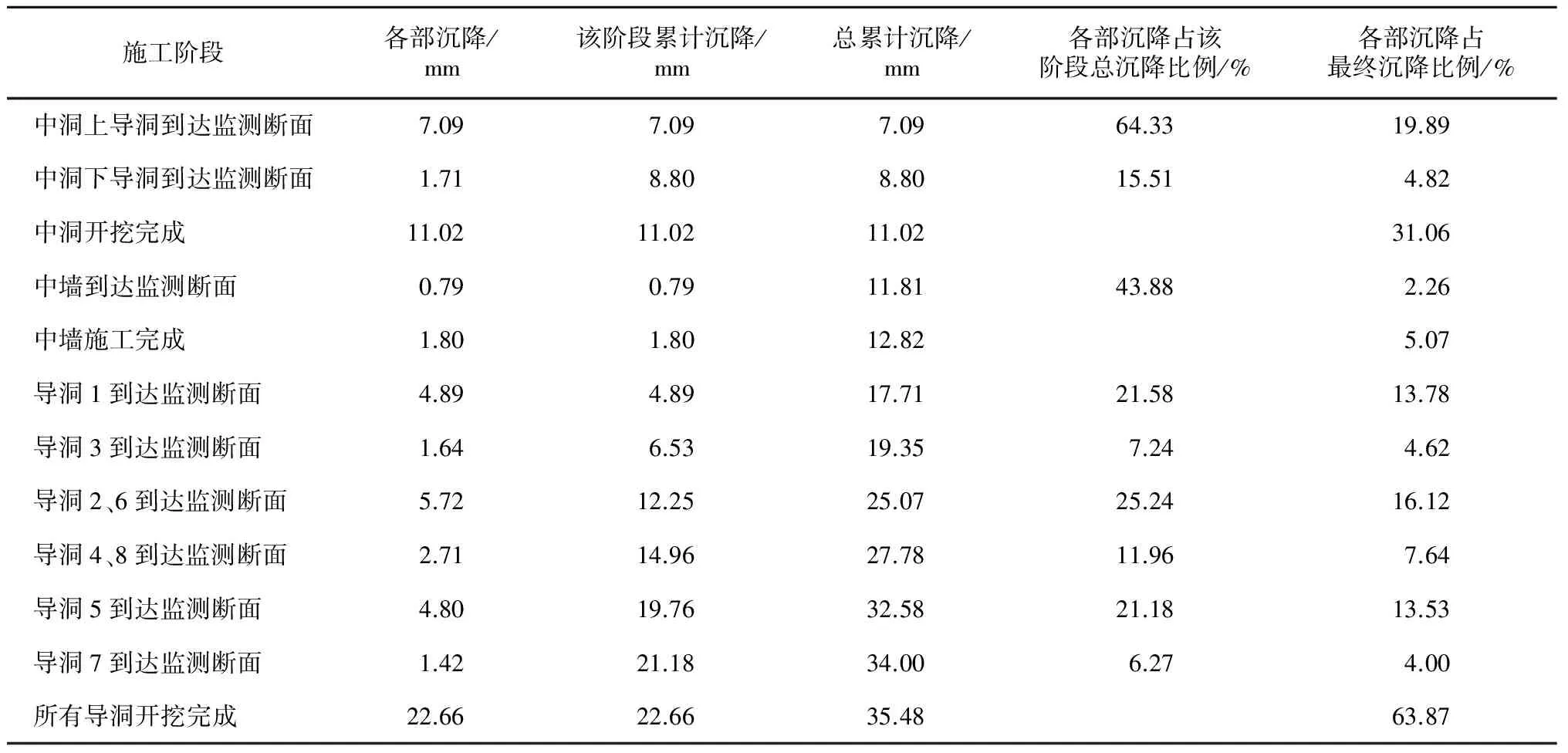
表4 地表沉降随施工过程变化情况

3.2 地表沉降纵向变化过程

3.2.1 中洞开挖地表沉降纵向变化过程

中洞开挖过程中,以监测断面中心点为观测点,观测点沉降随开挖过程的变化如图4所示。

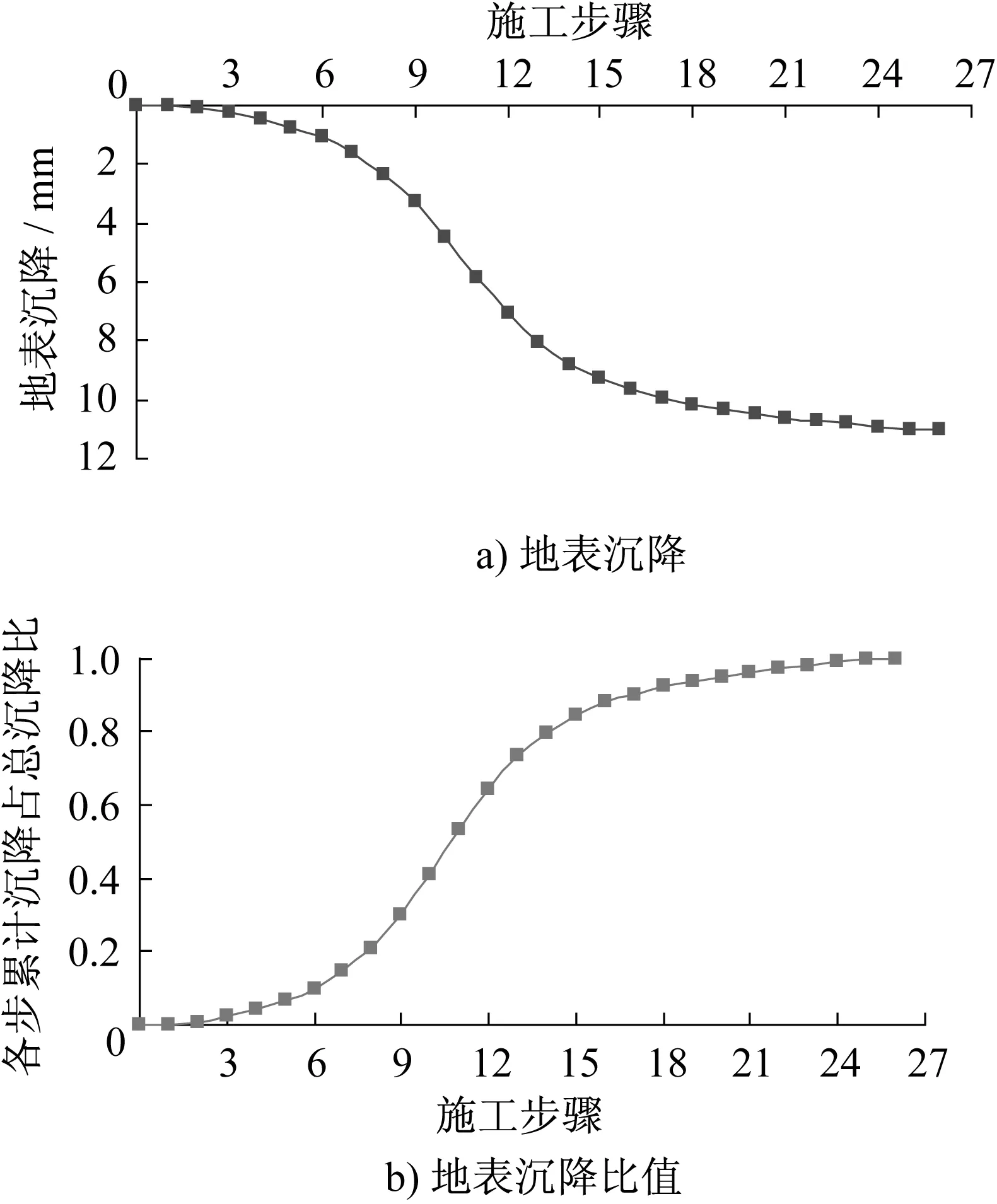
图4 中洞开挖完后地表A点纵向沉降

由图4可知,观测点纵向沉降分为3个阶段。当开挖到第4步时,观测点沉降开始受开挖影响;在开挖到第8步之前,地表沉降缓慢增长,到第8步时累计沉降量为2.3 mm,占最终沉降的21.1%。之后,地表沉降随掌子面的推进迅速增长;在开挖到第16步之后,地表沉降增长速度变缓,这之前中洞上方累计沉降量为9.68 mm,占最终沉降的87.8%。综上可知:地表纵向沉降3个阶段沉降占比分别为21%、67%、12%;每个阶段所在范围分别为-16 m～-8 m(约为-3B～-1.5B)，-8 m～8 m(约为-1.5B～1.5B)，以及1.5B之后。

3.2.2 两侧导洞开挖地表沉降纵向变化过程

两侧导洞开挖过程中,以监测断面中心点为观测点,观测点位移随开挖过程的变化如5所示。由图可知,观测点纵向沉降分为3个阶段,开挖到第4步时,观测点沉降开始受开挖影响;在开挖到第12步(导洞1掌子面到监测断面)之前,地表沉降缓慢增长;到第12步时累计沉降分别为4.8 mm,占最终沉降的21%;之后,地表沉降迅速增长,当开挖到第26步(导洞7掌子面到监测断面)之后,地表沉降增长变缓,这之前累积沉降量为21.2 mm,占最终沉降的92.35%。综上可知,地表纵向沉降中3个阶段沉降占比依次为21%、71%、8%。地表纵向沉降速率最快的阶段所在范围为-5B～5B。

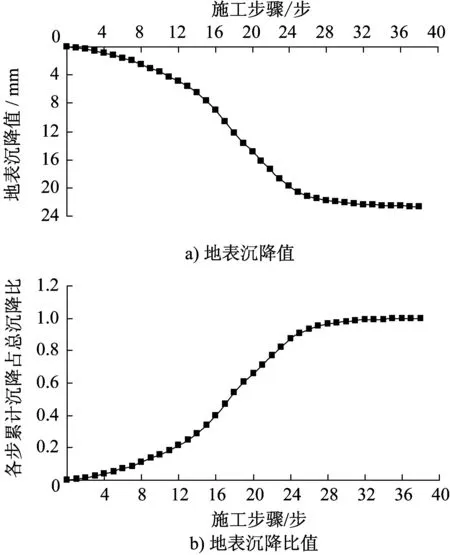
图5 两侧导洞施工完后地表A点纵向沉降

4 现场监测结果分析

4.1 现场监测方案

在实际施工过程中,对地表沉降进行监测,隧道里程YDK4+943.848处监测点布置如图6所示。图中A1～A11为沉降观测点。本工程监测等级为一级,为确保路面和地下管线的正常运行以及隧道施工期间的安全,要求地面沉降累计值为30 mm[11]。

4.2 地表沉降横向变化监测分析

实测地表沉降横向变化如图7所示。由图可知,中洞施工完后,地表沉降曲线关于隧道中心线对称,最大值为9.8 mm,占最终沉降的32%,沉降槽宽度为16 m,横向影响范围为40 m。中墙施工完后,沉降最大值为11 mm,占总沉降的36.52%,且地表沉降曲线形状基本没变化。两侧导洞施工完成后,地表沉降最大值为29.6 mm,发生在隧道中心线处,满足规范要求。这与模拟结果基本一致。

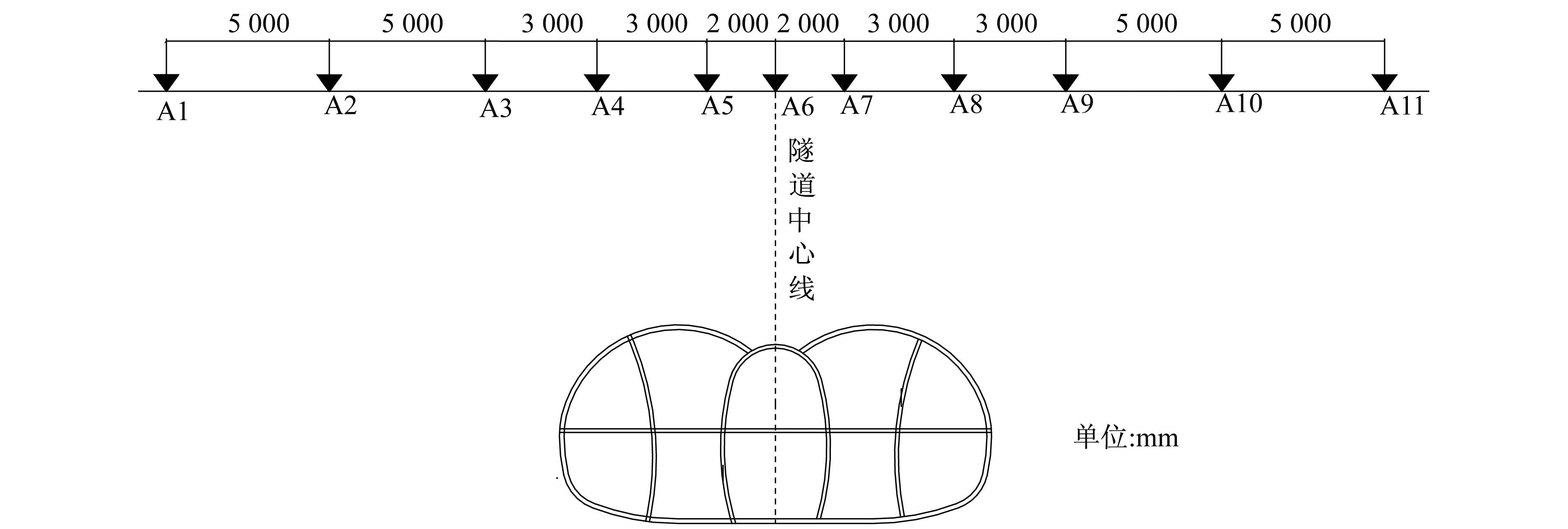
图6 地表横向监测点布置图

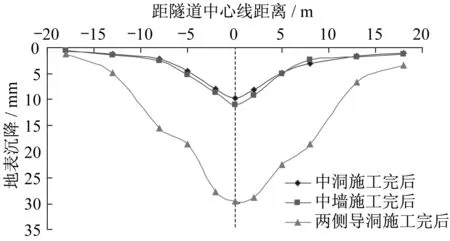
图7 实测地表横向沉降曲线

4.3 地表沉降纵向变化监测分析

实测两侧导洞开挖地表沉降纵向变化曲线见图8。由图可知,当导洞1掌子面距监测断面16 m时,观测点A6开始受导洞开挖的影响。在导洞1开挖到监测断面之前,地表沉降缓慢增长,导洞1开挖到监测断面时,地表沉降为4.6 mm,占总沉降19.1%。从导洞1开挖到监测断面至导洞7开挖到监测断面,地表沉降迅速增长,导洞7开挖到监测断面时,地表沉降为21.15 mm,占总沉降的88%。之后,地表沉降缓慢增长,直到稳定,稳定时沉降值为24.03 mm。这与模拟结果吻合较好。

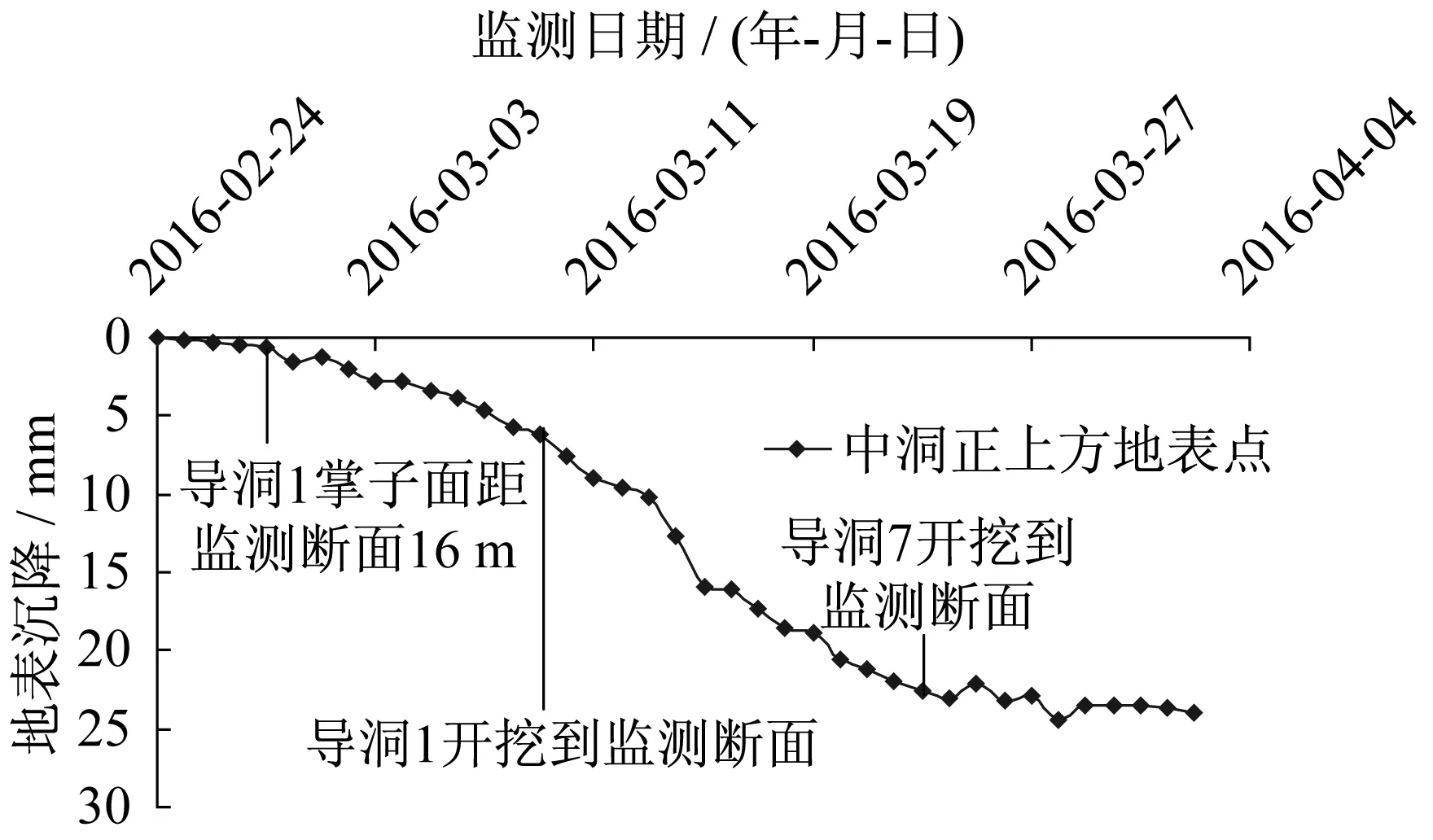
图8 实测两侧导洞开挖地表纵向沉降曲线

5 结论

通过FLAC3D软件对西安地铁4号线飞天路站到航天大道站区间双连拱隧道进行了三维数值模拟,分析了地表横向和纵向变形规律,并用现场实测数据加以验证,得到如下结论:

(1) 在隧道施工过程中,每个阶段引起地表沉降差异较大。中洞开挖引起的地表沉降占最终沉降的30%,其中上导洞开挖是引起地表沉降的主要部分,占64%。中墙开挖引起地表沉降占最终沉降的5%。两侧导洞开挖引起地表沉降占最终沉降的65%,导洞1、3、2和6、4和8、5、7开挖引起地表沉降占该阶段总沉降的21%、7%、25%、11%、21%、6%,其中上导洞开挖是引起沉降的主要部分,占67%。因此在施工上导洞时,可通过加密小导管和在掌子面全断面处注浆来加强初期支护。

(2) 在隧道两侧施工过程中,地表纵向沉降曲线均分为3个阶段:缓慢增长阶段,迅速增长阶段,缓慢增长阶段。但不同施工中地表沉降迅速增长阶段所在范围不同,对于中洞施工,在监测断面前后1.5倍单个导洞宽度范围内沉降增长最迅速;对于两侧洞室施工,在监测断面前后5倍单个导洞宽度范围内沉降增长最迅速。当施工在该范围内时,应及时施加初期支护,加强地表监测,并通过监测信息指导施工。

[1] 胡庆安,夏永旭,王文正.双连拱隧道施工过程的三维数值模拟[J].长安大学学报(自然科学版),2005,25(1):48-50.

[2] 任安菊.连拱隧道开挖过程空间应力应变研究[D].长春:吉林大学,2010.

[3] 杨萌.双连拱隧道开挖及支护全过程仿真分析[J].中国水运,2013,13(12):144-148.

[4] 李润军,单仁亮,廖秋林，等.CRD+CD法实现双连拱大断面暗挖施工的关键技术[J].公路交通科技,2014(4):194-198.

[5] 周文瑞.探讨高速公路双连拱隧道的施工[J].黑龙江交通科技,2013(2):134-136.

[6] 黄喜雄,何东洪.复杂地区条件下大跨双联拱隧道暗挖技术[J].广东土木与建筑,2014(9):44-47.

[7] 李强,王明年,李玉文.双联拱隧道两种中墙的空间力学效应分析[J].岩土力学,2006,26(4):667-972.

[8] 曹云钦,王小林.浅埋偏压联拱隧道中墙优化分析[J].岩土工程学报,2006,28(4):537-540.

[9] 时亚昕,王明年,李强.浅埋双连拱隧道的合理选用[J].地下空间与工程学报,2005,1(6):948-951.

[10] 吴波,高波,索晓明,等.城市地铁小间距隧道施工性态的力学模拟与分析[J].中国公路学报,2005,18(3):84-89.

[11] 中华人民共和国住房与城乡建设部.城市轨道交通工程监测技术规范:GB 50911—2013[S].北京:中国建筑工业出版社,2013.

Surface Settlement Caused by Shallow Double-arch Tunnel Construction in Loess Land

LIU Xinjun

Based on the double-arch tunnel project between Flying Road Station and Space Avenue Station on Xi′an metro Line 4, software FLAC3Dis used to simulate the surface settlement during the construction stage when two side chambers are excavated by cross diaphragm (CRD) method, the calculated results are compared with the measured data for the interval. The result shows that the surface settlement caused by the excavation of the two side chambers accounts for 65% of the total settlement, the top heading excavation accounts for 67% of the total settlement. It is clear that the construction of the two side chambers of the top heading is the key to control the final surface settlement. The growth rate of surface settlement is larger in the monitoring section before and after 1.5 times of a single heading width range as the middle of the tunnel is excavated, in the monitoring section before and after 5 times of a single tunnel width range as the two side chambers are excavated. Therefore, the monitoring should be strengthened and the initial support be applied in time when the construction is carried out within the certain range.

double-arch tunnel; surface settlement; numerical simulation

TU 433

10.16037/j.1007-869x.2017.05.009

2016-06-07)