地铁列车振动实测与共振理论分析

乔小雷 张允士 张 楠

(1.南京地铁运营有限责任公司,210012,南京; 2.北京交通大学土木建筑工程学院,100044,北京∥第一作者,工程师)



地铁列车振动实测与共振理论分析

乔小雷1张允士2张 楠2

(1.南京地铁运营有限责任公司,210012,南京; 2.北京交通大学土木建筑工程学院,100044,北京∥第一作者,工程师)

为研究地铁列车的竖向振动机理,以南京地铁1号线南延线某区间工程为背景,推导了考虑车钩约束的地铁列车运动方程,对车体的自由振动进行现场测试,得到地铁车辆的自振特性,据此分析其共振条件,并对地铁运行时引起的列车振动进行测试,验证了理论分析结果的正确性。结果表明:车速越高，车辆的载客率越高,桥梁周期性不平顺引起的外荷载输入频率越接近于车辆的卓越自振频率,导致车体共振概率越大;车速较低、车辆的载客率较低时,桥梁周期性不平顺引起的外荷载输入频率越小于车辆的卓越自振频率,导致车体共振概率越小。

地铁; 车辆; 共振

First-author′s address Nanjing Metro Operation Co.,Ltd.,210012,Nanjing,China

近年来,随着轨道交通的快速发展,轨道交通带来的振动问题越来越受到人们的关注。该问题通常可分为轨道交通引起的沿线建筑物的环境振动问题，以及车体本身振动问题。目前对于轨道交通引起的环境振动对周围建筑物的影响以及环境振动的预测已有较为深入的研究[1-4]。同时对于车体自身的振动问题,国内外的研究者也取得了一系列成果:文献[5]依托现场试验,提出一种更有效的评价车体振动的方法;文献[6]提出一种模态参数方法解决列车振动问题;文献[7]针对高速列车结构的振动特性进行了探讨;文献[8]针对车速在100～140 km/h行驶时机车引起的车体颤振机理进行了详细阐释;文献[9]创新性地考虑了车体柔性下的车-桥系统动力响应;文献[10]针对轮对的纵向振动,机车车辆轮对踏面剥离问题进行了研究。南京地铁1号线南延线JY站往返JM站高架区间自运营开通以来存在列车通过时产生不明原因的上下振动现象。列车过大振动不仅影响乘客的舒适度,而且有可能危及高架桥的寿命安全。有研究发现，弹性车体共振被激发时其动力响应被显著放大[11];车辆运行时,受线路和各种激励的作用,将引起车体整车或车体局部振动,如果这种振动超过某一限度,将严重影响乘客的舒适性[12]。为查明振动真实原因并消除可能存在的病害,为今后相关问题整改进行技术积累,开展了本课题研究,旨在彻底查找振动原因,提出切实可行的车体振动控制措施。

1 地铁列车分析模型与自由振动实测

根据结构动力学的基本原理,当荷载频率与结构物的自振频率相等或接近时,体系将发生共振,引起很大的动力响应。地铁列车在以某一稳定速度正常行进时,车轮受到轨道支撑处周期性力的作用,如果外荷载的频率接近车体的自振频率,就会引起车体的共振,加剧列车在行进时的振动效应。文献[13]研究发现，当车体的竖向1阶弯曲频率与车体空点头响应频率吻合时,将产生剧烈的弹性振动,从而影响承载舒适性和车体结构的疲劳寿命。该区间桥梁观测结果未发生拍振现象,排除了车桥之间共振的可能性。所以本文将车辆振动过大的原因归结于车辆系统与其输入激励频率接近导致的车体共振上,为此着重研究车辆共振条件,即当外荷载输入频率等于车辆自振频率时发生的共振状态。所以，准确获得实际列车弹簧刚度系数,建立与实际状态更相符的地铁列车模型,较为准确地获得车体自振频率，对于研究地铁列车共振尤为重要。

1.1 地铁列车动力学分析模型

将1列由6节车辆组成的地铁列车,依次编号为A车、B车、C车、C车、B车、A车。尽管在多数车-桥动力分析中均不考虑车辆与车辆之间的耦合关系,但由于实测中激励较小,测量的车辆为B车,其前后均有其他车辆的约束作用。为表征该约束作用,本文假定所测车辆的车体前后端均为弹簧约束,弹簧计算参数见图1。

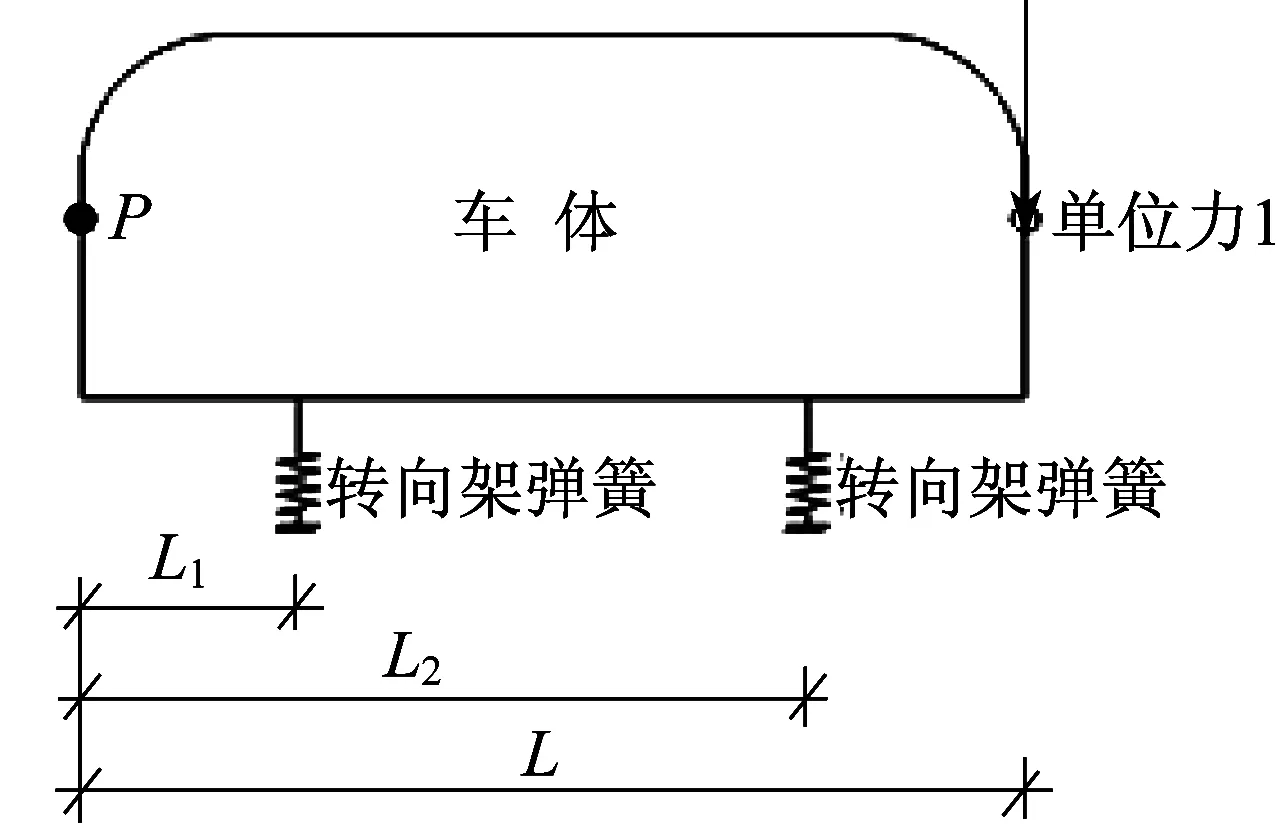
图1 车体弹簧约束的计算参数示意图

当车体右端作用单位力时,设位置为L1处的转向架弹簧变形量为δ,对车体左端P点取矩:

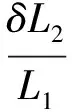
(1)

式中:

L1——左端转向架弹簧到车体左端的距离;

L2——右端转向架弹簧到车体左端的距离;

K——每一转向架一系、二系弹簧的总刚度，且

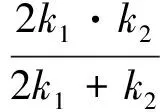
(2)

式中：

k1——一系悬挂弹簧刚度系数;

k2——二系悬挂弹簧刚度系数。

因此,车体右端的等效弹簧约束刚度为:

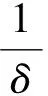
(3)

考虑等效弹簧后,车体模型见图2所示。图2中,ke是车体两端约束弹簧刚度系数;m2、m1分别是车体、转向架质量;c2、c1分别是一系悬挂轮对及二系悬挂转向架的阻尼系数;d1是轴距之半,d2为转向架定距之半;I2、I1分别是车体及转向架的转动惯性距。

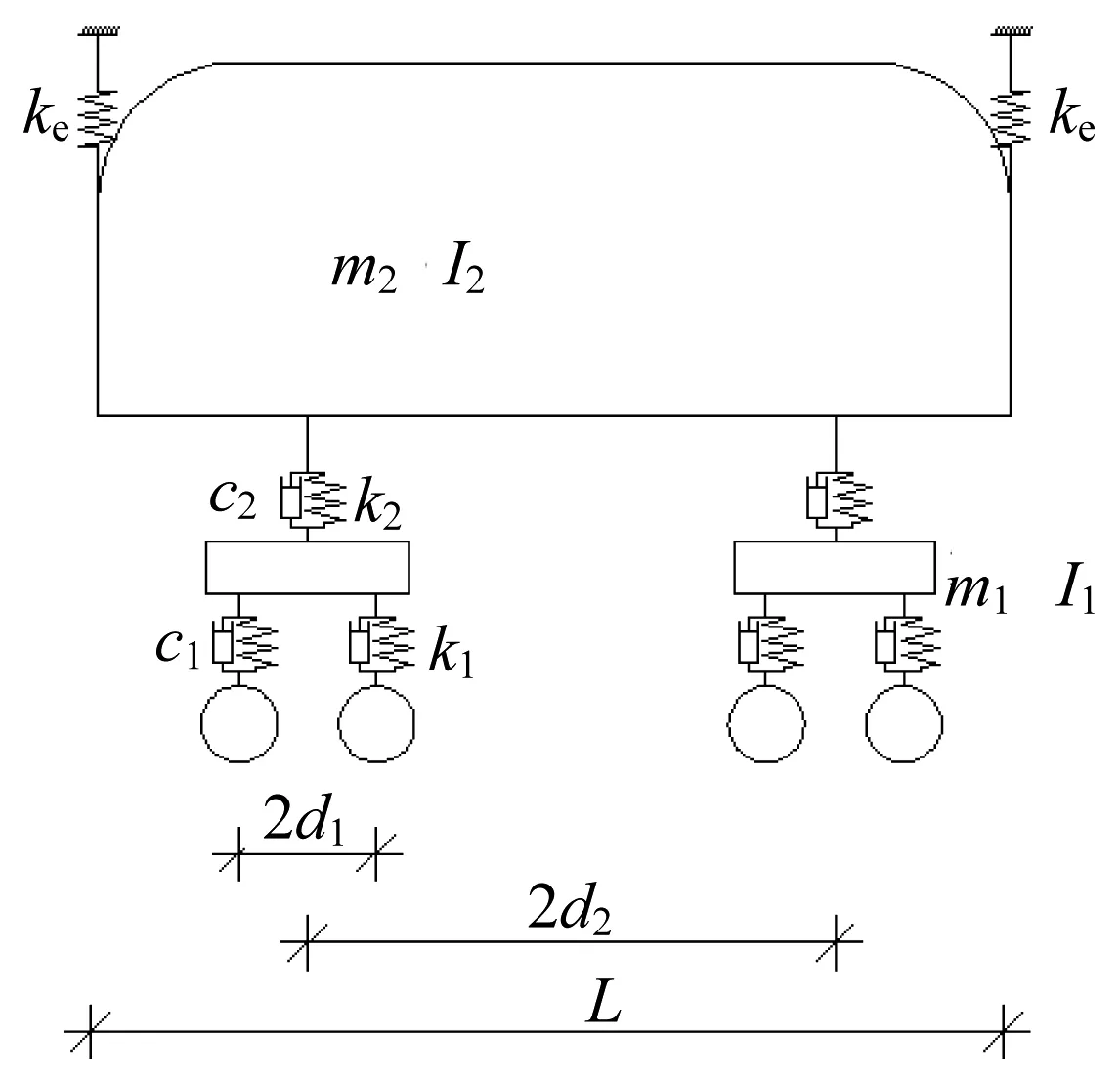
图2 车辆刚体动力学模型

经计算,车体的质量矩阵M及考虑等效弹簧的刚度矩阵K为:

其中:

由此,建立车辆系统的自由振动方程为:

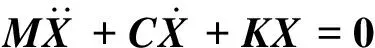
(4)

式中:

C——阻尼矩阵;

X——位移向量。

根据车辆基本参数(见表1),可计算得到车辆系统的自振频率。

大量研究表明,地铁列车运行一定时间后,其悬挂刚度参数会发生一定程度的改变,车体刚度参数的改变会导致车辆在运行时产生较大的振动,故车体的弹簧刚度系数应基于试验结果来进行调整。

1.2 车体自由振动现场实测

为了解所研究地铁车辆的真实悬挂参数,在地铁车辆段内进行了车体自由振动测试。测量中,在列车不同位置以人员跳起为激励,测量激励后列车前、后部车厢地面的自由振动。测点布置在前、后转向架处车体纵向轴线上,如图3所示。

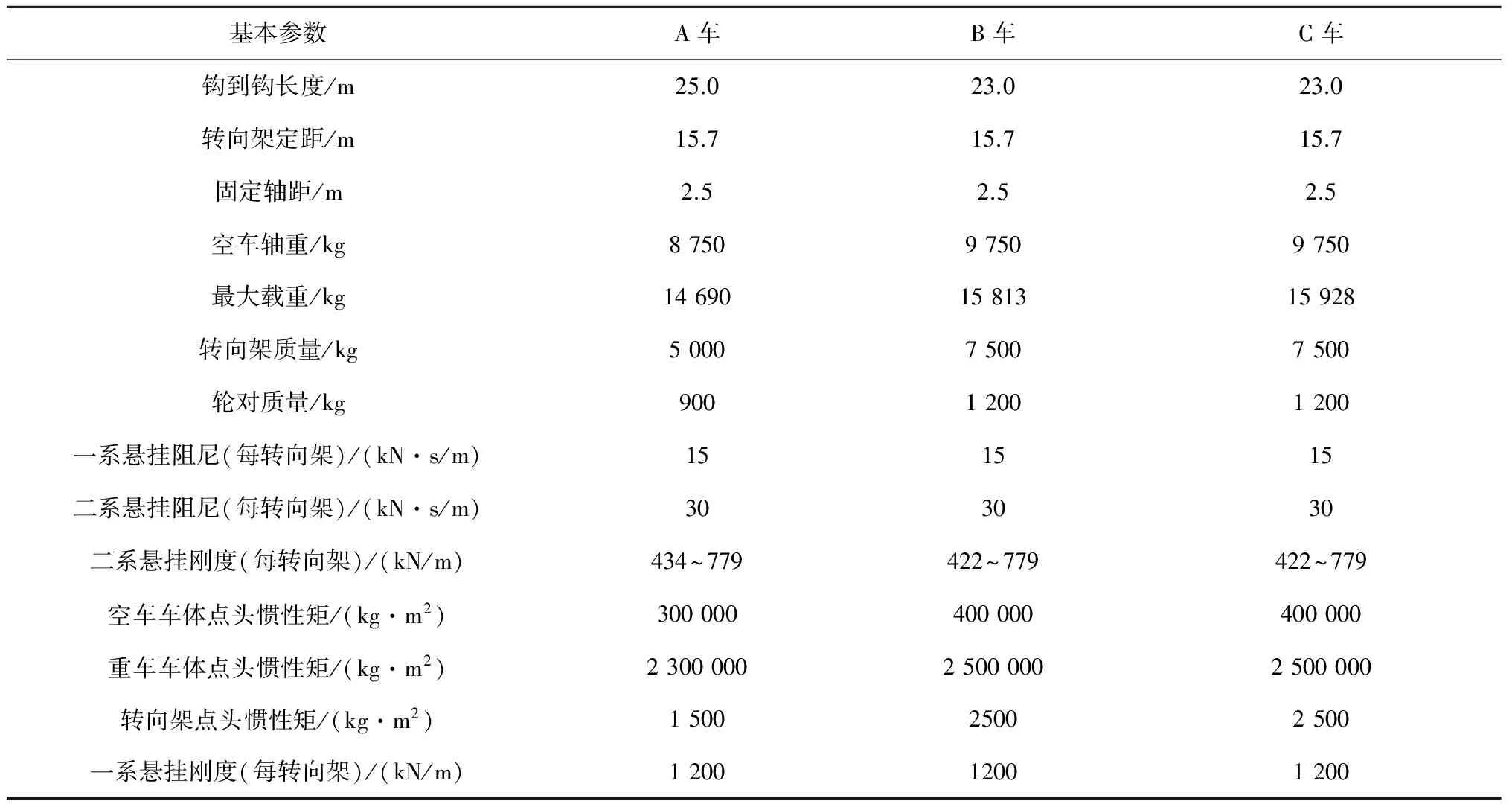
表1 车辆基本参数表

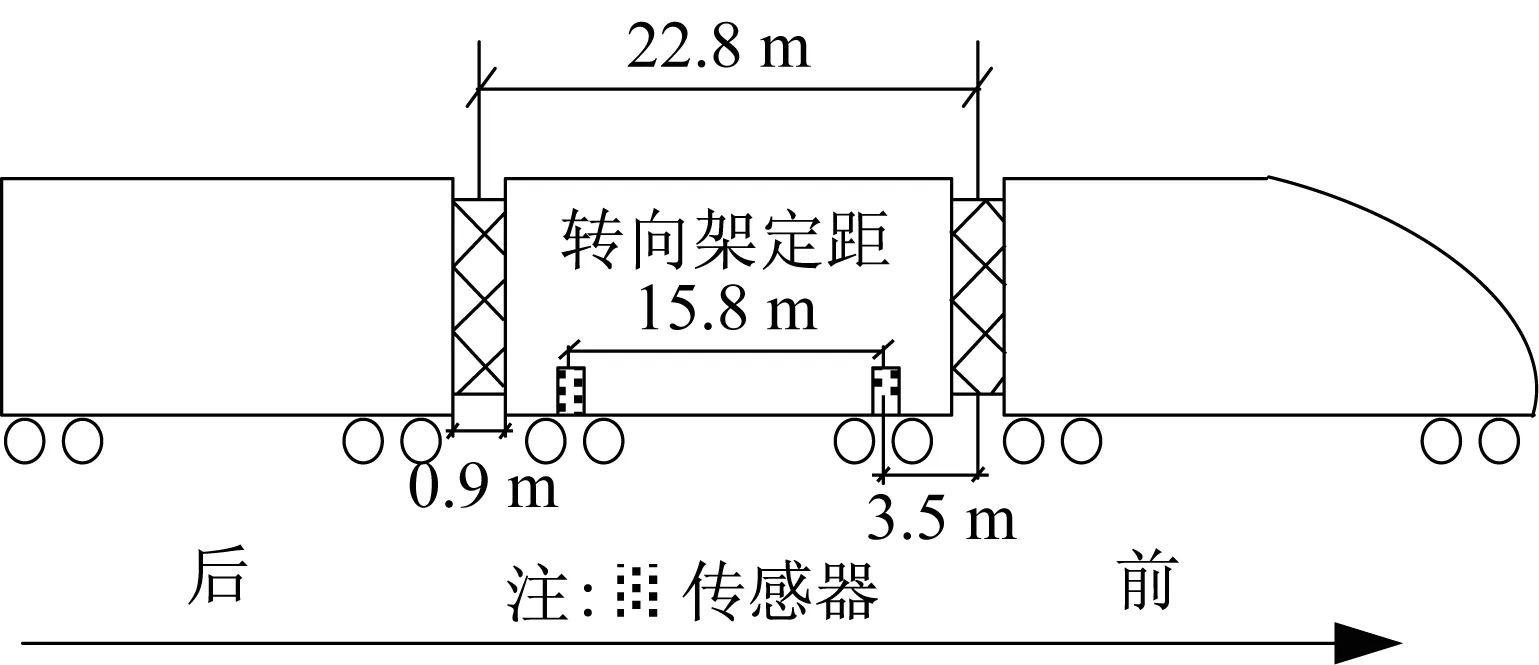
图3 车体自由振动测试的测点布置

试验中车体加速度采用北京东方振动和噪声技术研究所生产的INV-3018A型24位高精度USB采集仪、中国地震局工程力学研究所生产的941B型超低频测振仪，以及北京交通大学研发的BJTU-DZ3型测振仪底座,测量地铁正常运营条件下的车体振动。

测试中,采样频率为256 Hz。人员依次在车辆中部、车辆前部及车辆后部起跳,引起车体自由振动,采集车体竖向加速度时程,如图4所示。每测次分析前10次起跳记录,研究每次起跳后0.25 s起共计4 s的加速度记录。每测次共有40 s的时域记录数据。将其进行傅里叶变换(FFT)及模态识别，经分析,各测次均可识别车体的前两阶振动,且两车振动频率相同(见表2)。

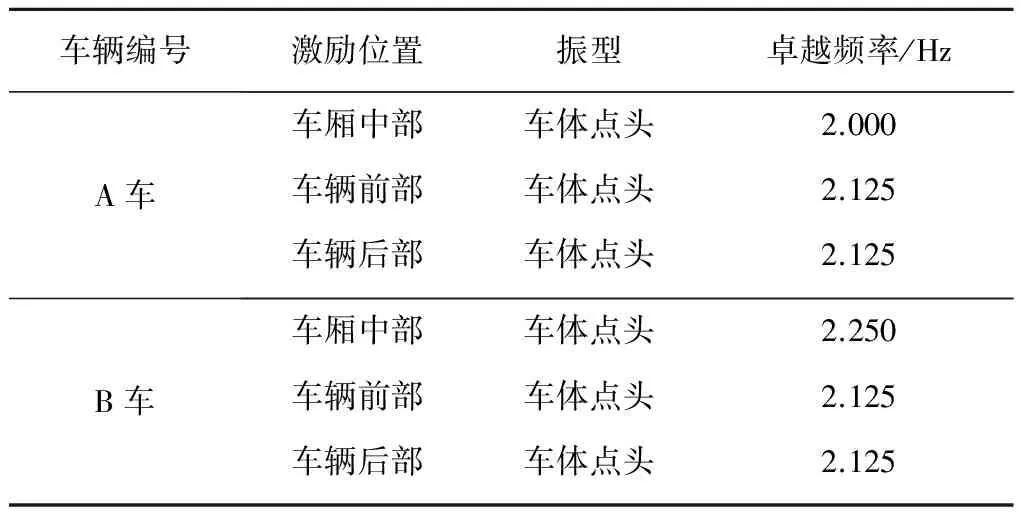
表2 车体自由振动频率

由表2可见,所测量的两节车辆的频率极为接近,测得的振型均为车体点头,卓越频率介于2.000～2.250 Hz之间。经调整,当其二系悬挂刚度为600 kN/m时,车体点头频率数值符合实测结果。故在后续计算中,将车体空载时二系悬挂刚度取为600 kN/m,满载时取为779 kN/m。由于激励点在前后转向架位置处,在车辆中间起跳也并非严格位于车辆中心处,故实测中沉浮响应成分不明显。由此得到A车、B车、C车在不同满载率条件下的自振频率，见表3。

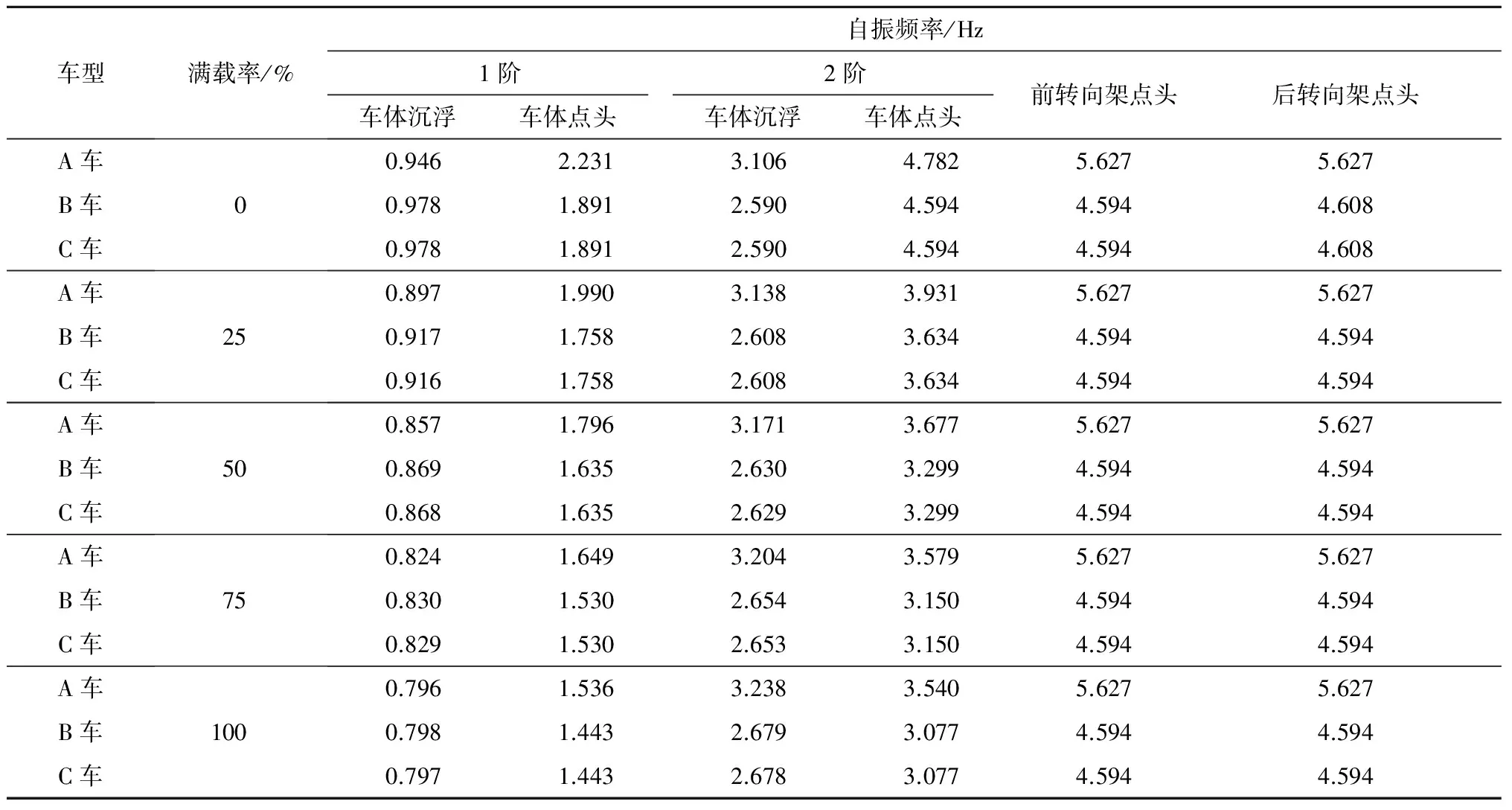
表3 车辆自振频率计算

1.3 正常运营条件下地铁列车共振条件分析

考虑车桥的耦合动力相互作用,将桥对车的作用力作为车体受到的外部激励。由共振条件可知,当车体受到外部激励的频率与车体自身的自振频率一致时,车体将发生共振。此处,外荷载仅指列车通过桥跨结构的周期性线路不平顺,本区段桥梁典型跨长为30 m。考虑列车速度范围50～80 km/h,其外荷载输入频率见表4所示。

表4 桥梁周期性不平顺引起的外荷载输入频率

对比表3及表4分析发现,在所有车型、满载率及车速条件下,车辆卓越自振频率均高于桥梁周期性不平顺引起的外荷载输入频率。但是车速越高,车辆的载客率越高,桥梁周期性不平顺引起的外荷载输入频率就越接近于车辆的卓越自振频率;车速越低,车辆的载客率越低,桥梁周期性不平顺引起的外荷载输入频率就越小于车辆的卓越自振频率。所以车速越高,满载率越高,车桥间发生共振的概率就越大;车速越低,满载率越低,车桥间发生共振的概率就越小。此结论亦验证了研究者在给定行车速度条件下列车振动测试的研究结果,即当车体振动过大时,控制车速为减振可供选择的方法之一。

需要说明的是,尽管满载率越高,车辆频率越低,与输入荷载卓越频率越接近,但满载状态下列车质量大,共振程度有可能反而降低。此外,较多文献表明,人体组织亦对列车有减振作用。因此,上述对比结果不应解释为满载率越大,共振程度越大。

2 地铁运营条件下车辆振动现场实测与共振条件分析

为了进一步分析验证地铁列车振动过大的原因是否是由于车辆共振所致,进行了地铁运营条件下车体振动测试，即测量地铁列车车厢地板的振动。测试主要是在JM至JY区段内测量正常行驶列车车厢地板处的三方向振动加速度时程,测量中采样频率为256 Hz,采样时间为列车正常运行在各区段内的行驶时间。其中，振动分析指标的计算方法如下:将测量竖向加速度数据分为时长1s的时间段,分别按GB 10071—88《城市区域环境振动测量方法》规定的方法及相应的计权因子,计算每个时间段的VLz振级;A0为各时段加速度最大值中超越概率0%者,即最大者,亦各时间段中VLz振级最大者;A5、A10、A20分别为各时段VLz振级超越概率为5%、10%、20%者;A50为各时段VLz振级超越概率为50%者,亦即中位数。本文以A50数据为评价列车振动程度的主要指标。测试记录以及各测次车体振动数据见表5。

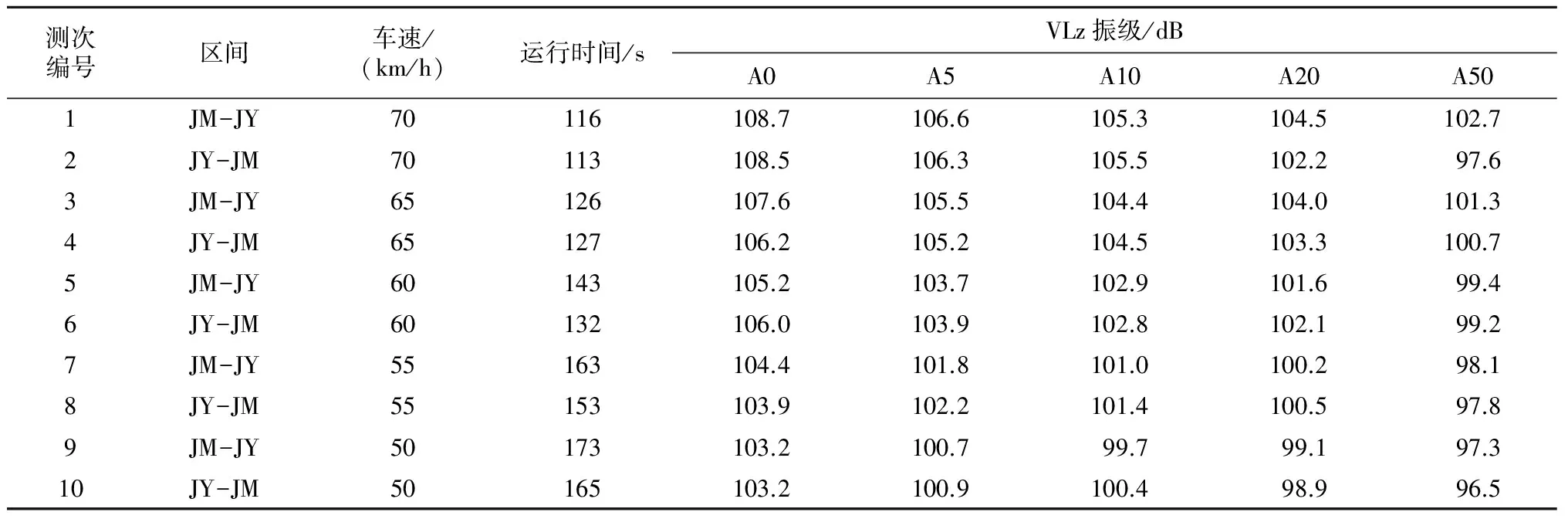
表5 不同行车速度条件下列车振动测试表

由表5分析数据可见,随着列车速度提高,车体竖向振动加速度显著增大。A50分析数据显示，车速70 km/h时,车体振动VLz振级较车速50 km/h约增加6 dB,即前者有效振动加速度为后者的2倍。可见,当车体振动过大时,控制车速为减振可供选择的方法之一。此外,JM开往JY方向车体振动略大于JY开往JM方向,其原因除两侧线路不平顺条件差异等偶然因素外,有可能是线路平纵断面设计等因素造成。一般而言,列车高速通过曲线区段时,由于车-桥系统存在横向-竖向耦合关系,也会造成车体竖向振动幅值增加。

3 结论

本文通过对南京地铁1号线南延线地铁列车在JM至JY站之间正常运营时车体振动现场实测与分析,得到以下研究结论:

(1) 车体自由振动测试显示,所测车辆振型均为车体点头,卓越频率介于2.000～2.250 Hz之间。

(2) 车速越高，车辆的载客率越高,桥梁周期性不平顺引起的外荷载输入频率就越接近于车辆的卓越自振频率,导致车体共振概率越大;车速越低，车辆的载客率越低,桥梁周期性不平顺引起的外荷载输入频率就越小于车辆的卓越自振频率,导致车体共振概率越小。

(3) JM往返JY区段所测得的振动明显较其他区段大。且随列车速度的提高,车体竖向振动加速度显著增大。原因是该区段内车辆的参振质量低，以及两侧线路不平顺条件差异等偶然因素造成,也有可能是线路平纵断面设计等因素造成。

[1] 蒋通,张昕.高架轨道交通引起环境振动的实测与数值模拟[J].同济大学学报(自然科学版)，2004,32(5):565-569.

[2] 夏禾,张楠,曹艳梅.列车对周围地面及建筑物振动影响的试验研究[J].铁道学报,2004,26(4):93-98.

[3] 陈建国,夏禾,肖军华,等.列车运行对周围地面振动影响的试验研究[J].岩土力学,2008,29(11):3113-3118.

[4] 李小珍,刘全民,张迅,等.铁路高架车站车致振动实测与理论分析[J].岩土力学,2014,49(4):612-618.

[5] DIANA G,CHELI F,COLLINA A,et al.The development of a numerical model for railway vehicles comfort assessment through comparison with experimental measurement [J].Vehicle System Dynamics,2002,38(3):165-183.

[6] ZHOU J S,SHEN G,ZHANG H,et al.Application of modal parameters on ride quality improvement of railway vehicles[J].Vehicle System Dynamics,2008,46(1):629-641.

[7] 郭涛,赵明,张迅,等.高速列车车体结构振动特性分析[J].计算机辅助工程,2013,22(3):9-13.

[8] 戴焕云.机车车辆车体颤振机理分析及解决方案[J].内燃机车,2008(7):16-18.

[9] 王英杰.考虑车体柔性的车-桥动力响应分析及行车舒适性影响因素研究[D].北京:北京交通大学,2011.

[10] 马卫华.轮对纵向振动及其相关动力学影响研究[D].成都:西南交通大学,2007.

[11] 王英杰,时瑾,魏庆朝.单车过桥下弹性车体共振与消振现象分析[J].振动与冲击,2015,34(2):1-8.

[12] 郭金莹,王勇,石怀龙.地铁车辆地板共振机理分析及解决方案[J].机械,2013,40(9):6-9.

[13] 周劲松,孙文静,宫岛.铁道车辆几何滤波现象及弹性车体共振分析[J].同济大学学报(自然科学版)，2009,37(12):1653-1657.

Test of Rail Transit Vehicle Vibration and Analysis Resonance Theory

QIAO Xiaolei, ZHANG Yunshi, ZHANG Nan

In order to analyse the vertical vibration mechanism of subway vehicles in the background of the south extension on Nanjing subway Line 1, a subway train motion-equation considering coupling constraints is developed. Through in-situ measurement of the free vibration of vehicles body, the natural vibration characteristics of metro train is obtained. Then the resonance condition is analyzed, the vehicles vibration induced by metro train is tested on the site, which verifies the correctness of the theoretical analysis result. It shows that the higher train speed, the higher load factor; when the external input frequency induced by bridge periodic irregularities comes closer to the vehicle′s natural frequency, the resonance probability of vehicle will increase. While with lower train speed and load factor, the external input frequency induced by bridge periodic irregularities will be smaller than vehicle′s natural frequency, which will decrease the resonance probability of vehicle consequently.

metro; vehicle; resonance

TB 533+.2;U 270.1+6

10.16037/j.1007-869x.2017.05.006

2015-06-10)