运用动量定理妙解电磁感应中的单杆问题
2017-06-19李元法
李元法
(湖北省当阳市第一高级中学,湖北 当阳 444100)
·试题研究·
运用动量定理妙解电磁感应中的单杆问题
李元法
(湖北省当阳市第一高级中学,湖北 当阳 444100)
新物理考试大纲将选修3-5的内容纳入必考内容,这将使高考命题更加突出主干内容的整体性、综合性,更能考查学生的核心素养.巧用动量定理妙解电磁感应现象中的单杆问题,正是符合上述高考的变革要求,这类问题既强调基础,又兼顾综合,还能考查学生运用所学知识分析问题、解决问题的能力,值得广大师生重视
动量定理;电磁感应;单杆模型
1 引言
2017年湖北省普通高考考试大纲规定了考试内容与形式,对指导高考内容改革、规范高考命题都有重要意义.其中将选修3-5的内容纳入必考内容,可使动量和牛顿运动定律、能量相结合,不但保证了经典力学体系的完整性,而且使高考命题更加突出考试内容的整体性.电磁感应现象中的单杆问题主要应用了动量定理,单杆模型是电磁感应现象中的重要模型,常见的模型有三种类型:单杆和电阻相结合、单杆和电容器相结合、单杆和电源相结合.
2 单杆和电阻相结合模型
单杆在磁场中运动产生的动生电动势和电阻相结合,相当于电源和电阻组成闭合回路.利用动量定理和闭合电路欧姆定律、法拉第电磁感应定律相结合,可以方便地求出金属杆运动的距离、速度和运动时间.
2.1 单杆和电阻相结合在水平面运动
例1:如图1所示,一水平放置的光滑足够长平行导轨上放一质量为m的金属杆,导轨间距为L,导轨的一端连接一阻值为R的电阻,其他电阻不计,磁感应强度为B的匀强磁场垂直于导轨平面.当金属杆以初速度v0水平向右运动时,试求金属杆在导轨上向右移动的最大距离.

图1
解:金属杆受重力、支持力和水平向左的安培力作用;设金属杆运动时间为Δt,取水平向右为正方向.
2.2 单杆和电阻相结合在竖直方向运动
例2:如图2所示,竖直放置的平行金属导轨的上端跨接一阻值为R的电阻,导轨间距为L.质量为m的金属棒MN可沿平行导轨竖直下滑,不计轨道与金属棒的电阻,在垂直导轨平面有两个方向垂直纸面向里、磁感应强度为B的匀强磁场区域.两磁场的上边界相距为d,将金属棒MN从第一个磁场上方高h处由静止释放,已知金属棒MN刚进入第一个磁场时速度为v0,金属棒MN刚进入第二个磁场时速度也为v0.

图2
求:(1) 金属棒MN刚离开第一个磁场时的速度;
(2) 金属棒MN由静止释放到离开第二个磁场时的运动时间.
解:(1) 设金属棒穿过磁场克服安培力做功为W克,金属棒运动时间为t、穿过任意一个磁场的时间为Δt、金属棒刚离开磁场时的速度设为v.

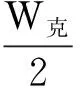
金属棒在竖直方向先做自由落体运动,进入磁场后做变减速运动;然后做匀加速运动,再变为减速运动,难以用运动学公式求出变速运动的时间,巧用动量定理可迅速求出全过程的运动时间.
3 单杆和电容器相结合模型
当单杆和电容器相结合时,杆运动切割磁感线产生电动势,电容器会出现充、放电现象,电路中形成电流,杆受到安培力作用,做变速运动最后达到稳定状态,做匀速运动,应用动量定理和电流的定义式、电容的定义式、法拉第电磁感应定律相结合可以简洁地求出杆稳定运动的速度和电容器所带电荷量.
3.1 单杆和电容器相结合在水平面运动
例3:如图3所示,U型导轨固定在水平面上,导轨左端接一电容为C的电容器,电容器原来不带电.导轨间距为L且足够长.有一质量为m、长度为L的导体棒放在导轨上,设导体棒、导轨的电阻均可忽略,导体棒和导轨间的摩擦也不计,导轨处于方向垂直水平面(即纸面)向下的匀强磁场B中.今给导体棒ab一个向右的初速度v0,试求:(1) 导体棒ab的最终运动速度;

图3
(2) 导体棒ab稳定运动时电容器所带电荷量.
解:(1) 导体棒向右运动,切割磁感线产生感应电动势使电容器充电,当电容器C极板间电压与导体棒产生的感应电动势相等时,电路中没有电流,ab棒不再受安培力,向右以速度v0做匀速运动.
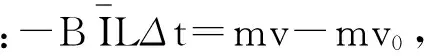

3.2 单杆和电容器相结合在竖直方向运动

图4
例4:如图4所示,竖直方向上有两条足够长的平行导轨ab、cd,导轨间距为L.导轨上端接有一平行板电容器,电容为C.导轨处于水平向里的匀强磁场中,磁感应强度大小为B.在导轨上放置一质量为m的金属棒MN,让金属棒由静止开始向下运动,且在运动过程中保持与导轨垂直并良好接触.重力加速度大小为g,忽略所有电阻.求:
(1) 电容器极板上积累的电荷量与金属棒速度大小的关系;
(2) 金属棒的速度大小随时间变化的关系.
解:(1) 设金属棒MN运动的速度大小为v,由法拉第电磁感应定律得:E=BLv.


4 利用动量定理解析单杆和电源相结合模型
金属杆和电源相结合组成回路,杆为负载,受安培力作用将做变速运动.金属杆运动切割磁感线产生动生电动势,反过来影响电路使金属杆做变加速运动.利用动量定理可灵活地求出通过金属杆的电荷量、金属杆运动的时间.
4.1 单杆和电源相结合在水平面运动
例5:如图5所示,金属棒ab质量m=20g,放在相距L=0.5m的两根光滑的金属导轨上,磁感应强度B=4T,方向竖直向上,电源电动势E=3V,导轨距地面高度h=0.2m,当电键闭合后,金属棒被抛到水平距离s=1.6cm的地面上,重力加速度取10m/s2.求:
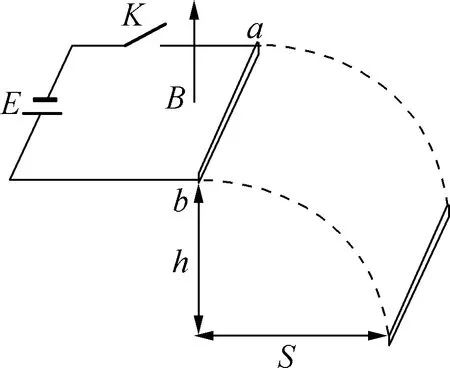
图5
(1) 电键闭合瞬间金属棒获得的速度;
(2) 电键闭合瞬间通过金属棒的电荷量.


4.2 单杆和电源相结合在竖直方向运动

图6
例6:如图6所示,竖直放置的平行金属导轨上端跨接一电动势为E=2V的电源,不计轨道和电源的内阻.质量为m=100g的金属棒MN可沿平行导轨竖直下滑,金属棒电阻R=2Ω,竖直导轨处在匀强磁场中,匀强磁场垂直导轨平面向里且B=1T.两导轨足够长,间距为L=0.5m,当金属棒MN在磁场中由静止释放后,竖直向下运动距离h=2m时达到稳定状态.
求:(1) 金属棒达到稳定状态时的速度;
(2) 金属棒MN在磁场中由静止释放到达稳定状态运动的时间.
解:(1) 金属棒向下运动切割磁感线产生动生电动势,做加速度越来越小的加速运动,达到稳定状态后做匀速运动.

(2) 设对金属棒经过时间t达到稳定状态.

孟卫东,何龙.高考物理改革,我们怎么学?[J].中国考试,2017,(1).
