浅析以层层递进的方式建立合理模型在物理教学中的作用——以“电磁滑轨中的双杆问题”为例

邬扬杰

(浙江省宁海中学 浙江 宁波 315600)

1 课堂引入

教学片段1:以单杆模型为例.

【例1】如图1所示，两条平行的光滑金属轨道置于水平桌面上，轨道足够长，轨道间距为L，金属棒P置于轨道上，始终与轨道垂直且接触良好，金属棒P的质量为m，速度为v，方向向右，磁场方向垂直水平桌面向下，大小为B.距金属棒P很远的位置有一电阻，阻值为R2，此时轨道与金属棒P、电阻R2构成闭合回路，金属棒P接入闭合回路的电阻为R1，所有轨道电阻忽略不计.

图1 例1题图

提出问题,学生回答如下：

(1)金属棒P将做什么运动？

学生回答：金属棒向右做加速度减小的减速运动直至静止.

(2) 若此时金属棒P的速度为vP，则加速度是多少？

学生回答：

电流

加速度

(3)整个过程产生的焦耳热是多少？

学生回答：根据能量守恒定律

(4)整个过程流过金属棒P或R2的电荷量为多少？

学生回答:可以用动量定理来计算[1]，对金属棒P分析

(5)计算出金属棒P运动多少距离后停下？(师提示：q与磁通量的变化量有关)

学生回答:

所以有

设计意图:抓住由简入难的思想，以单杆模型为铺垫，为了引出双杆模型；题目设计一环扣一环，难度按梯度上升，使学生投入课堂，积极思考并解决相关问题.

教学片段2:引出电磁滑轨类问题中的多种模型,如图2所示.

图2 电磁滑轨类问题多种模型

设计意图 使学生清楚电磁滑轨问题复杂多样，题目千变万化，并正式引出“双杆模型”.

2 分析多种双杆模型

教学片段3：双杆模型——等长同一磁场.

【例2】(在例题1的基础上稍做改变)如图3所示，若电阻R2换成一根阻值同样为R2的不固定的金属棒Q，质量为m2，初速度为零，金属棒P的质量为m1，其他条件不变.

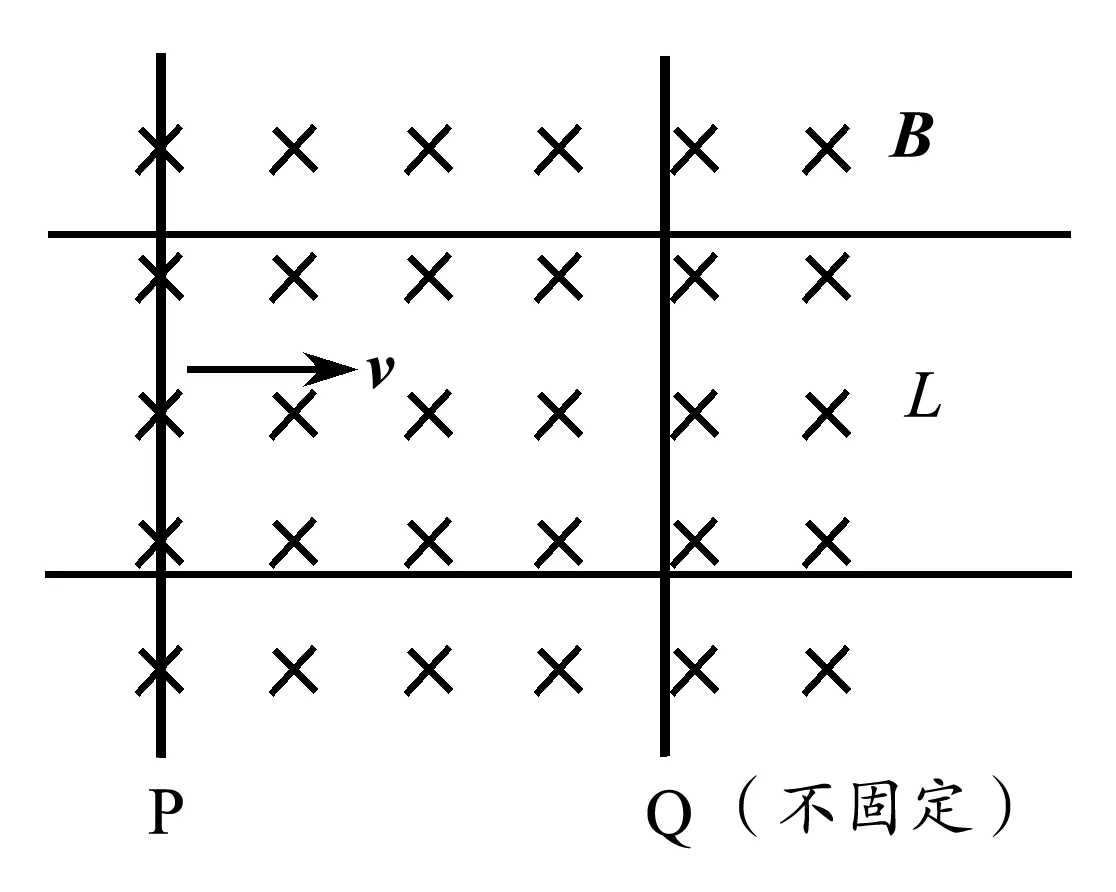
图3 例2题图

提出问题，学生回答如下：

(1)金属棒P，Q将分别做什么运动？

学生回答：P做减速运动，Q做加速运动，最终两者以共同的速度做匀速直线运动.

(2) 若此时金属棒P和Q的速度分别为vP和vQ，则加速度分别是多少？

学生回答：

加速度都逐渐在减小.

老师补充：若vP=vQ，两根棒加速度都为零，接下来一起做匀速直线运动.

(3) 最终共同速度是多少？(师提示对金属棒P,Q运用动量定理求解)

学生回答：

m1v=(m1+m2)v共

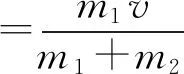
(4) 整个过程流过金属棒P或Q的电荷量为多少？(师提示对某一金属棒运用动量定理求解)学生回答对棒Q分析，利用动量定理

BLq=m2v共

得

(5) 整个过程产生的焦耳热是多少？

学生回答:利用能量守恒定律

总结 整个运动过程中可以分为两部分，金属棒P和Q做变速运动与匀速运动.整个过程产生的焦耳热其实是金属棒P和Q做变速运动时产生的，金属棒P和Q做匀速直线运动时不会产生焦耳热.不会产生焦耳热意味着这个过程中回路中无电流.为什么会没有电流？这是因为金属棒P和Q产生的感应电动势等大反向，BLv1=BLv2，得出v1=v2=v共，所以我们可以利用感应电动势等大反向来判断出匀速时两根金属棒的速度大小关系.

3 学以致用

【习题1】(2018年温州新力量联盟期中试题)如图4所示，NQ和MP是两条平行且倾角为θ的光滑金属轨道，在两条轨道下面，在Q,P处接着QT和PS两条平行光滑的金属轨道，轨道足够长，所有轨道电阻忽略不计.金属棒ab,cd放在轨道上，始终与轨道垂直且接触良好.金属棒ab,cd的质量均为m，长度均为L，且金属棒的长度恰好等于轨道的间距，它们与轨道构成闭合回路，金属棒ab的电阻为2R，cd的电阻为R.磁场方向均垂直于导轨向上(不考虑PQ交界处的边界效应，可认为磁场在PQ处立即变为竖直向上)，磁感应强度大小为B.若先保持金属棒cd不动，ab在沿导轨向下的力F的作用下，开始以加速度a沿倾斜轨道向下做匀加速直线运动.经过t0时间，ab棒恰好到PQ位置，此时撤去力F，同时释放金属棒cd，重力加速度为g，求：

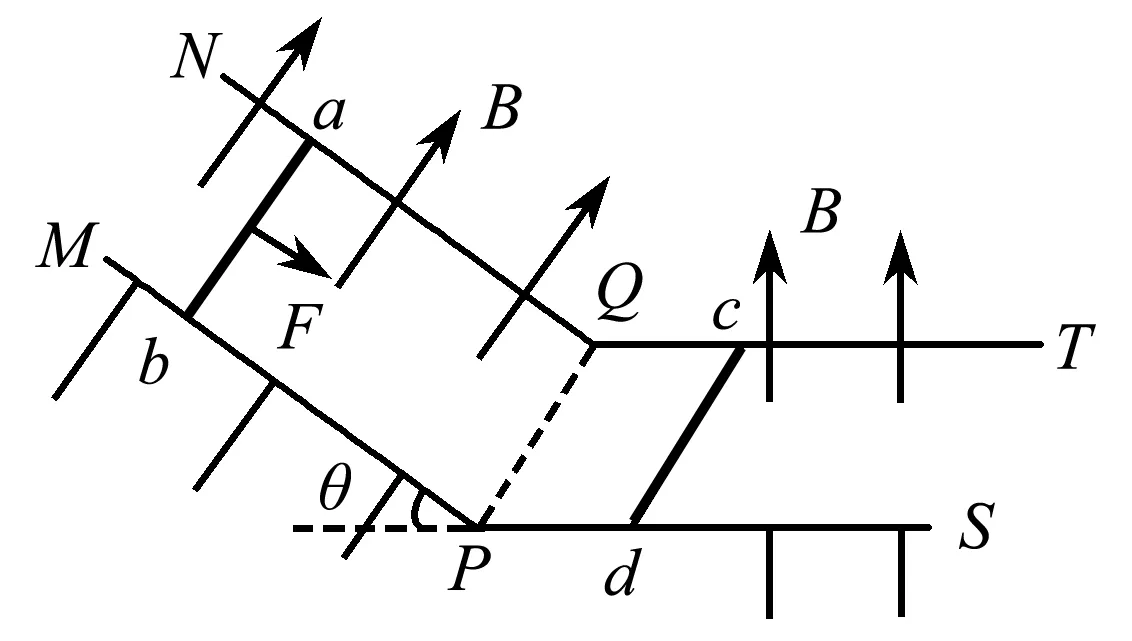
图4 习题1题图

(1)棒ab匀加速运动过程中，外力F随时间t变化的函数关系；

(2)两金属棒从撤去F，直到最后达到稳定后的运动过程中，金属棒cd产生的热量Q；

(3)两金属棒从撤去F，直到最后达到稳定后的运动过程中，通过金属棒cd的电荷量q.

得

(2)

v1=at0mv1=2mv2

则

v2=0.5at0

则

(3)

则

教学片段4:双杆模型——不等长同一磁场

【例3】(在例2的基础上稍作改变)如图5所示，水平面内固定两对足够长的平行光滑金属导轨，左侧两导轨间的距离为L1，右侧两导轨间的距离为L2，左、右侧的两导轨间都存在大小为B，方向竖直向下的匀强磁场，其他条件不变.

图5 例3题图

提出问题，学生回答如下：

(1)金属棒P与Q将分别做什么运动？

学生回答：金属棒P做加速度减小的减速运动直至匀速.金属棒Q加速度减小的加速运动直至匀速.

(2) 若此时金属棒P和Q的速度分别为vP和vQ，则加速度分别是多少？

学生回答：

(3) 最终匀速(稳定)的速度满足什么关系？(师提示感应电动势等大反向)

学生回答:

BL1v1=BL2v2

则

(4) 金属棒P和Q的稳定速度分别是多少？

老师推导:对金属棒P和Q，由动量定理

-BL1q=m1(v1-v)

BL2q=m2v2-0

(5) 整个过程流过金属棒P或Q的电荷量为多少？(师提示对某一金属棒运用动量定理求解)

学生回答:对棒Q分析，利用动量定理

BL2q=m2v2-0

得

【习题2】(河北省武邑中学2019届高三上学期第一次调研物理试题)如图6所示，水平面内固定两对足够长的平行光滑金属导轨，左侧两导轨间的距离为2L，右侧两导轨间的距离为L，左、右侧的两导轨间都存在大小为B，方向竖直向下的匀强磁场.两均匀的导体棒ab和cd分别垂直放在左、右两侧的导轨上，棒ab的质量为2m,有效电阻为2r，而棒cd的质量为m、有效电阻为r，其他部分的电阻不计.原来两棒都处于静止状态，现给棒ab一大小为I0,方向平行导轨向右的冲量使棒ab向右运动，在达到稳定状态时，两棒均未滑出各自的轨道.求：

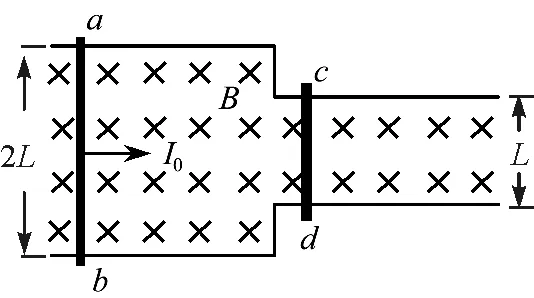
图6 习题2题图

(1)棒cd中的最大电流Im；

(2)棒cd的最大加速度；

(3)两棒达到稳定状态时，各自的速度大小.

(3)稳定时

2LBvab=BIvcd

-2LBIt=2mvab-2mv0

BILt=mvcd-0

则

教学片段5:双杆模型——等长不同磁场，如图7所示.

图7 双杆等长不同磁场

双杆模型——不等长不同磁场，如图8所示.

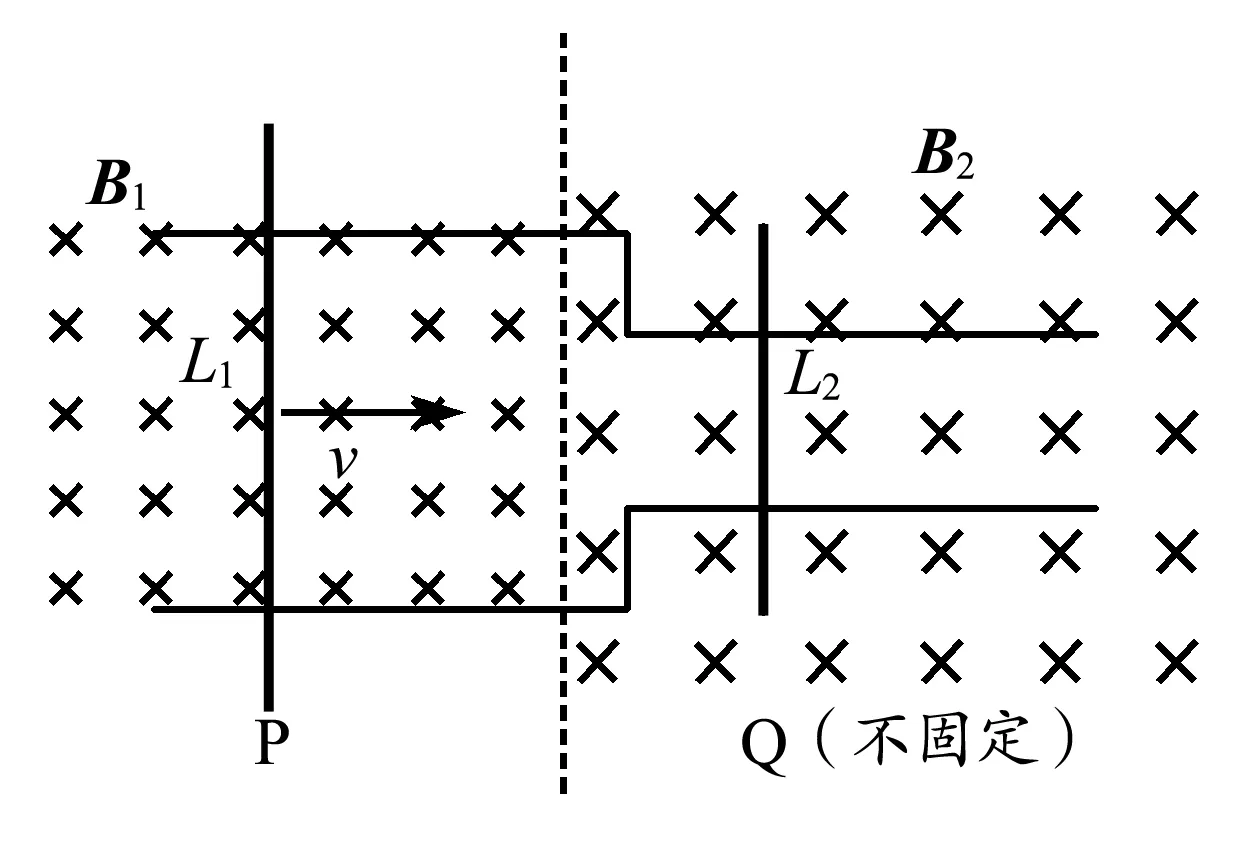
图8 双杆不等不同磁场

提出问题，学生回答如下：

(1)两根金属棒最终匀速(稳定)的速度满足什么关系？运用什么方法？

学生回答：两根金属棒产生的感应电动势等大反向.

(2) 金属棒P和Q的稳定速度分别是多少？可以如何计算？

学生回答：分别对两根金属棒列动量定理表达式.

设计意图：从等长同一磁场到不等长同一磁场再到等长不同磁场和不等长不同磁场，模型在发生变化，题目难度和复杂程度在不断加大，但我们的解题思路和方法手段有很大的相似之处，让同学们感受到这些相同之处，并且加深理解，有助于他们解决这类题目.

4 课堂总结

从以上模型我们可以得到一些结论，在冲量型双杆模型中最终的电流会趋近于一定值——零，导体棒的加速度也会趋近于一定值——零.其实不管是单杆还是双杆，不管是冲量型还是拉力型，不管是等宽还是不等宽，最终电路中电流会趋近于一个定值(可以为零，也可以不为零)，导体棒的加速度趋近于一定值(可以为零，也可不为零).

双杆模型在处理最终速度时，紧扣电流这条主线，再结合动量定理或动量守恒，能量守恒，一般情况下可以解决问题.

为什么双杆电路中的电流或加速度会趋近于一个定值？这是因为导体棒的速度与时间关系是一个以e为底的指数函数，现在笔者简单推导如下：

以冲量型等长双杆模型为例，如图9所示，金属轨道光滑，棒a质量为m1，电阻为R1，棒b质量为m2，电阻为R2，现给棒a初速度v0，求棒b速度与时间的关系.

图9 冲量型等长双杆模型

设某时刻t，棒a速度为v1，棒b速度为v2,则

(1)

再根据系统动量守恒得

m1v0=m1v1+m2v2

(2)

(3)

将式(3)带入式(1)，整理可得

(4)

化简得

(5)

(6)

整理可得

(7)

积分可得

(8)

式中C1为积分常量，则

(9)

式中τ为某常量.

冲量型双杆模型中最终两棒中的速度不变，电流不变，导体棒的加速度不变.

拉力型双杆模型中最终两棒中的速度差不变，电流不变，导体棒的加速度不变.

笔者以“电磁滑轨中的双杆问题”为例，从双杆运动情况、加速度、稳定状态、电荷量、动量、能量等几个角度多方位地剖析整个运动情形，并且从最简单的等长同一磁场双杆模型入手，一步步改变题目的条件，使题目的难度逐步增加.从等长同一磁场双杆模型到不等长不同磁场双杆模型，以层层递进的方式建立合理的物理模型，由简入难，使学生尽可能地掌握电磁滑轨中的双杆模型；同时，可以有效地培养学生的思维能力与探究精神.