聚焦高考中的计数问题
2017-06-19河南省平顶山市一中李智恒
■河南省平顶山市一中 李智恒
聚焦高考中的计数问题
■河南省平顶山市一中 李智恒
计数问题种类繁多,方法多变,但从高考的角度来看,重点考查同学们利用“加法和乘法”这两个原理与“排列数和组合数”这两个公式解决实际问题的能力。按元素的性质“合理分类”和按事件发生的连续过程“准确分步”,始终是处理计数问题的关键所在。
一、构建组合模型求解计数问题的实际应用
1.选人和组数的有关问题。
(1)(2015年上海卷理科)在报名的3名男教师和6名女教师中,选取5人参加义务献血,要求男、女教师都有,则不同的选取方式的种数为____。(结果用数值表示)
(2)(2015年四川卷理科)用数字0,1, 2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( )。
A.144个 B.120个
C.96个 D.72个
解析:(1)由题意得,任选5人再去掉全选5名女教师的情况即可,-=120。
(2)比40000大的偶数,第一位必为4或5。当第一位为4时,末位有0和2两种选择,故有2×4×3×2=48(个)偶数;当第一位为5时,末位有0、2、4三种选择,故有3×4× 3×2=72(个)偶数。共有120个,选B。
点评:选人与顺序无关,可构建组合数的模型计数。注意“含”与“不含”的问题:“含”,则先将这些元素取出,再由另外元素补足;“不含”,则先将这些元素排除,再从剩下的元素中选取。通常直接分类复杂时,考虑逆向思维,用间接法处理。
2.交换、握手问题。
(2012年安徽卷理科)6位同学在毕业聚会活动中进行纪念品的交换,任意2位同学之间最多交换一次,进行交换的2位同学互赠1份纪念品。已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为( )。
A.1或3 B.1或4
C.2或3 D.2或4
解析:设6位同学分别用a,b,c,d,e,f表示。若任意2位同学之间都进行交换,则需要进行C26=15(次)交换,已知共进行了13次交换,说明有2次交换没有发生,此时可能有两种情况:
①由3人构成的2次交换,如a→b和a→c之间没有发生交换,则收到4份纪念品的有b,c2人。
②由4人构成的2次交换,如a→b和c→d之间没有发生交换,则收到4份纪念品的有a,b,c,d4人。故选D。
点评:交换、握手问题顺序确定,构建组合模型计数,注意特殊情况的剔除,如本题中的特殊情况由3人构成的2次交换和由4人构成的2次交换。
3.求二项展开式中某一项的系数。
A.56 B.20 C.-56 D.60
所以x7的系数为(-1)7=-56,因此答案为C。
点评:求二项展开式中某一项的系数,先分析该项的构成,再结合所给式,分析如何得到该项,利用组合知识求解,它源于二项式定理的推导过程。
二、特殊元素或特殊位置的“优先法”
1.特殊元素自然分组。
(2014年广东卷)从0,1,2,3,4, 5,6,7,8,9中任取7个不同的数,则这7个数的中位数是6的概率为____。
解析:要使6为取出的7个数中的中位数,则取出的数中必有3个不大于6,另外3个不小于6,将元素按性质分组,合理分类分步计数。从0,1,2,3,4,5, 6,7,8,9中任取7个不同的数,有C710种方法,若7个数的中位数是6,只需从0, 1,2,3,4,5中选3个,从7,8,9中选3个不同的数即有种方法。
故这7个数的中位数是6的概率为:
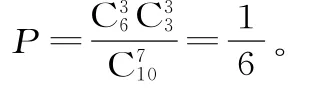
点评:依据中位数的意义,将7个元素合理分成2组,凸现合理分类与分步计数算概率的思维方法,它贯穿于排列组合应用问题的始终。
2.特殊位置合理分类。
(2014年四川卷)6个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有( )。
A.192种 B.216种
C.240种 D.288种
解析:可从甲所在位置入手合理分类,当甲在最左端时,有A55=120(种)排法;当甲不在最左端时,乙必须在最左端,且甲也不在最右端,有=4×24=96(种)排法。共有120+96=216(种)排法。选B。
点评:解决排列组合问题最基本的方法是位置分析法和元素分析法,若以位置为主,首先满足特殊位置的要求,再处理其他位置;若以元素为主,先满足特殊元素的要求,再处理其他元素。对于有限制条件的排列组合问题,可从限制元素(或位置)入手,优先考虑,先分类后分步,设计填空位的模型来求解。
三、相邻、不相邻(相离)、不全相邻问题的处理方法
1.相邻问题用捆绑法。
2位男生和3位女生共5位同学站成一排,若男生甲不站两端,3位女生中有且只有2位女生相邻,则不同排法的种数是( )。
A.60 B.48 C.42 D.36
解法1:从3位女生中任取2人“捆”在一起记作A,则A共有C23·A22=6(种)不同排法,剩下1位女生记作B,2位男生分别记作甲、乙,则男生甲必须在A、B之间(若甲在A、B两端,则为使A、B不相邻,只有把男生乙排在A、B之间,此时就不能满足男生甲不在两端的要求),此时共有6×2=12(种)排法(A左B右和A右B左),最后在排好的3个元素形成的4个空隙中选1个插入乙,所以,共有12×4=48(种)不同排法。
解法2:从3位女生中任取2人“捆”在一起记作A(A共有A23种不同排法),剩下1位女生记作B,两名男生分别记作甲、乙。为使男生甲不在两端可分三类情况:
第一类:女生A、B在两端,男生甲、乙在中间,共有6A22A22=24(种)排法;
第二类:“捆绑”A和男生乙在两端,则中间女生B和男生甲只有1种排法,此时共有6A22=12(种)排法;
第三类:女生B和男生乙在两端,同样中间“捆绑”A和男生甲也只有1种排法,此时共有6=12(种)排法。
排法共有24+12+12=48(种),选B。
点评:对于某些元素要求相邻的排列问题,先将相邻的元素“捆绑”起来,看成一个“大”元素与其余元素排列,然后再对“大”元素内部进行排列。对于有限制条件的排列问题,一般先从特殊元素和特殊位置入手,基本解法有直接法和间接法。
2.不相邻问题用插空法。
(2014年辽宁卷)6把椅子摆成
解析:这是一个元素不相邻问题,从结果入手设计插空法的模型。先排3个空位(无序),再在3个空位构成的4个空隙中插入坐人的3把椅子,3个人的顺序可交换,分步完成,有=24(种),选D。
点评:不相邻问题用插空法时,一般是先排没有限制条件的元素,再按要求将不相邻的元素插入排好的元素之间。
3.不全相邻问题采用“间接法”。
(2014年北京卷)把5件不同产品摆成一排,产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有____种。一排,3人随机就座,任何2人不相邻的坐法种数为( )。
A.144 B.120 C.72 D.24
解析:这是一个不全相邻问题,采用“间接法”,注意A、B相邻中含有A、C相邻的情形。先考虑产品A与B相邻,把A、B作为一个元素有种方法,而A、B可交换位置,所以有2=48(种)摆法;又当A、B相邻又满足A、C相邻时,有2=12(种)摆法。故满足条件的摆法有48-12=36(种)。
点评:相邻问题用“捆绑法”,不相邻问题用“插空法”,不全相邻问题常采用“正难则反”的策略,即用“间接法”求解,凸显“特殊化、模型化和一一对应思想”在计数中的具体应用。对于捆绑法,一般是将必须相邻的元素看作一个“大元素”,然后再与其余“普通元素”全排列,但不要忘记对“大元素”内的元素进行排列。
四、间接法和列举法求解错位排列问题
(1)同室4人各写1张贺年卡,先集中起来,然后每人从中各拿1张别人送出的贺年卡,则4张贺年卡不同的分配方式有( )。
A.6种 B.9种
C.11种 D.23种
(2)编号为1、2、3、4、5的5个球放入编号为1、2、3、4、5的5个盒子里,每盒只放1个,至多有2个对号入座的情形有____种。
解析:这两题分别为4个元素和5个元素的错位排列问题,用列举法或间接法求解。
(1)解法1:分类求解,设4人A,B,C,D写的贺年卡分别是a,b,c,d,当A拿贺年卡b,则B可拿a,c,d中的任何1个,若B拿a,则C拿d,D拿c;若B拿c,则D拿a,C拿d;若B拿d,则C拿a,D拿c。所以A拿b时有3种不同分配方法。同理,A分别拿c, d时也各有3种不同的分配方式。由分类计数原理知,4张贺年卡共有3+3+3=9(种)分配方式。
解法2:分步完成,让4人A,B,C,D依次拿1张别人送出的贺年卡。如果A先拿有3种,此时写被A拿走的那张贺年卡的人也有3种不同的取法。接下来,剩下的2个人都各只有1种取法。由分步计数原理可知,4张贺年卡不同的分配方式有:
3×3×1×1=9(种)。
解法3:树图列举法,如果把4个人依次抽取的结果用一个图表体现出来,就显得更加清楚。
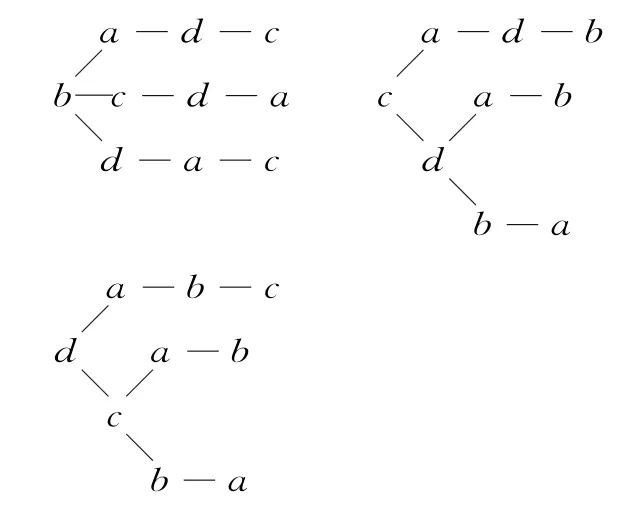
由图表可知,共有9种不同结果。
(2)至少或至多问题一般选用间接法。3个球的标号与盒子的标号一致的放法有种,只有4个球的标号与盒子的标号一致的放法没有,5个球的标号与盒子的标号一致的放法有1种,用排除法,至多有2个对号入座的情形有--1=109(种)。
点评:元素的错位排列可直接求解,如果某些元素不能排在某些特殊位置上,可先把某个元素按规定排入,再排另外元素,如此继续下去,借助树图列举法依次即可完成错位排列的问题。
(责任编辑 徐利杰)
