柱棒式超磁致伸缩能量收集器的设计与实验

孟爱华, 杨剑锋, 蒋孙权, 刘 帆, 刘成龙

(杭州电子科技大学 机械工程学院，杭州 310018)

柱棒式超磁致伸缩能量收集器的设计与实验

孟爱华, 杨剑锋, 蒋孙权, 刘 帆, 刘成龙

(杭州电子科技大学 机械工程学院，杭州 310018)

为了能够利用自然界中的振动能量，弥补传统微器件供能方式的不足。设计制作了一种以超磁致伸缩材料(GMM)为基础的振动能量收集装置，并通过实验加以验证其能量收集特性；首先，通过对超磁致伸缩材料物理特性的分析，进行了能量收集装置理论建模与仿真分析；然后，根据仿真分析的结果设计了一套柱棒式的超磁致伸缩能量收集器；最后，通过搭建实验平台进行了效果验证。实验结果表明：当输入激振信号频率fn不变，振动能量收集装置输出电压峰-峰值和输入振动信号的幅值Fm成正比；当输入振动信号幅值Fm不变，振动能量收集装置输出电压峰-峰值和输入激振信号的频率fn成正比；在激振应力最大值为2.54 MPa、频率100 Hz的正弦激振条件下，感应线圈100匝的实验条件下，超磁致伸缩振动能量收集器输出电动势峰-峰值为136.4 mV，与理论值(156 mV)符合较好，且波形一致。

振动；能量收集；超磁致伸缩材料

随着科技的发展，能源作为一切生产生活的源动力，关系着国家的整体发展，因此能源问题越来越受到各界学者和专家的密切关注。除了从根本上减少资源浪费，加大资源的利用效率外，发掘新型能源用于代替传统不可再生资源已经成为国内外学者的研究重点。在自然界中机械振动所产生的能量具有存在范围更广、不受气候与地域以及时间的限制等优点。因此，近年来被众多专家学者所重视，随之各种形式的振动能量收集技术也应运而生。现阶段主要的能量收集技术主要包括：电磁式、压电式、静电式、磁致伸缩式四类，且以前三种居多[1-2]。

近年来，随着对超磁致伸缩材料特性研究的不断深入，越来越多的专家学者提出了一种新型的能量收集技术即超磁致伸缩式能量收集技术。利用超磁致伸缩材料的维拉里效应，也称为压磁效应，即超磁致伸缩材料受到压应力的作用发生变形[3]，引起材料内部的磁通密度发生改变的现象。然后根据电磁感应定律，变化的磁场产生电场，回路中就会产生感应电动势，从而实现机械能向电能的转化。由于超磁致伸缩式振动能量收集方式相对于其他振动能量收集方式较为复杂，目前的相关研究报道较少，主要集中在几所国外院校。埃及开罗大学的Amr Adly和意大利萨尼奥大学的Daniele Davino对磁致伸缩材料的输出特性进行了分析并设计以稀土超磁致伸缩材料Terfenol-D为核心智能材料的能量收集装置模型[4]。Ueno等[5-7]在对铁镓合金(Galfenol)进行了相关性能分析的基础上，选择Galfenol作为其设计的能量收集装置的核心材料，设计出了一系列的试验样机。以上提到的关于超磁致伸缩式能量收集技术的模型的理论研究还不是很成熟，没有完善的理论体系，国内对这种方式的能量收集技术的研究还处在探索阶段[8]。因此，如何基于已有的理论利用磁致伸缩材料的超强的机电耦合特性进行能量收集，实现微型器件的自供能，是我们今后将要重点研究的工作。本文从现阶段国内外研究现状出发，设计制作一套柱棒式的超磁致伸缩能量收集装置，对棒状超磁致伸缩材料进行理论分析与建模，并通过实验对整个装置的能量收集特性进行讨论。

1 柱棒式超磁致伸缩振动能量收集的基本原理及理论模型

1.1 柱棒式超磁致伸缩振动能量收集的基本原理

超磁致伸缩材料具有多种物理效应，本文设计的能量收集器主要运用超磁致伸缩材料的压磁效应即维拉里效应，实现由周围环境的机械振动能到磁场能的转变，再由法拉第电磁感应定律实现由磁场能到电能的转变[9]。当偏置条件一定的条件下，外部应力σ能够改变材料内部有效磁场He进而影响材料中的磁化强度M。因此，可以用经典的机电耦合模型来描述超磁致伸缩棒中总的磁化强度M和应力σ的关系，其表达式为[10]：

(1)

式中：M表示总磁化强度；Man表示无磁滞磁化强度；Mirr表示不可逆磁化强度；σ表示施加在超磁致伸缩棒上的激振应力，可表示为σ=Fsin(ωt+φ)，其中F表示激振幅值，ω表示激振频率；E表示超磁致伸缩棒的杨氏模量；ξ表示单位体积能量耦合系数；c表示可逆系数。

其中无磁滞磁化强度Man和不可逆磁化强度Mirr，可以利用Jiles-Atherton物理模型描述求解，如式(2)所示[11]。

(2)

(3)

上述一阶线性微分方程的通解为

(4)

1.2 超磁致伸缩式振动能量收集的理论模型

由电磁感应定律可知感应线圈两端的感应电动势E与通过线圈的磁通量Φ的变化率成正比。如果不考虑漏磁，并且假定超磁致伸缩棒内部的磁感应强度B沿着长边中心线方向均匀分布，线圈的横截面积为A，则每匝感应线圈内部的磁通量为Φ=BA，从而线圈内的感应电动势可表示为：

(5)

式中：负号表示振动能量收集器的输出感应电压为负向；N表示感应线圈的匝数；Φ表示单匝线圈内部穿过的磁通量；t表示时间。

当不考虑温度变化的影响，在一定范围内，材料内部的磁化强度随施加的外应力增大而增大。本文研究的主要是基于超磁致伸缩材料的逆效应在能量收集领域的应用，利用的理论模型为人们经常用到的线性压磁模型[12]，公式为

(6)

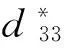
由电磁学原理可知，超磁致伸缩棒沿长度中心线方向的磁场强度Hl与总的磁化强度M之间的关系的表达式为：

(7)

式中：μ0表示真空磁导率，值为μ0=4π×10-7H/m；Hg表示由线圈中的感应电流产生的磁场；Hi表示外加总磁场磁场，包括外加偏置磁场H和感应电流产生的磁场Hg的和。

结合式(6)和式(7)得超磁致伸缩棒中的磁感应强度可表示为：

(8)

将式(8)代入式(5)得：

(9)

(10)

最后，将式(3)代入式(10)便可以得到振动能量收集装置中感应线圈产生的感应电动势和外加激振应力的关系，从而建立了能量收集的数学模型。

1.3 超磁致伸缩式振动能量收集的仿真分析

仿真参数设置如下：超磁致伸缩棒长度和直径分别为30 mm、10 mm；感应线圈均匀的分布于线圈骨架上，其匝数和长度分别为100 mm、30 mm。在实验室的环境中，能量收集装置的输入激振源可以分为：位移型激振源、应力型激振源和加速度型激振源。基于实验所用的模态激振器更容易确定位移激振函数，因此，本次仿真采用的输入激振源为位移型激振，当激励信号的振幅和频率分别为10 μm和100 Hz，由于超磁致伸缩棒和模态激振器的输出顶杆为刚性接触，在不考虑传递时的能量损失的情况下，对应的超磁致伸缩棒受到的激振应力表达式σ(t)=E·ε(t)=10+10sin(200πt+3π/2) MPa，如图1所示。

利用MATLAB软件，结合式(4)和式(9)可求得相应的输出感应电动势，如图2所示。相应的输出感应电动势峰-峰值为781 mV。

从图2可知，对理论模型进行仿真输出的感应电动势的表达式为E(t)=390.5cos(200πt+π/2) mV；能量收集装置的输出感应电动势的相位相对于输入激振应力滞后了π/2。这是由于磁致伸缩材料等铁磁材料的固有属性即磁滞特性引起的，当磁场强度从最大值逐渐递减时，磁感应强度不是按原来的曲线返回，而是沿着较原来曲线略高一点的曲线递减，正是由于铁磁体中磁感应强度的变化相对于磁场强度而言的滞后，从而引起了输出感应电动势的相位滞后于输入激振应力的相位。此外，输出的感应电动势波形出现了明显的畸变，不是标准的余弦波形。因此，通过能量收集装置直接产生的电能，不能够直接给微机电器件供电，需要做进一步的整流和滤波处理。

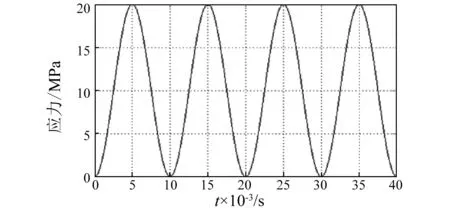
图1 正弦激振条件下的GMM棒应力随时间的变化Fig.1 The stress of GMM rod change over time with the condition of sine excitation

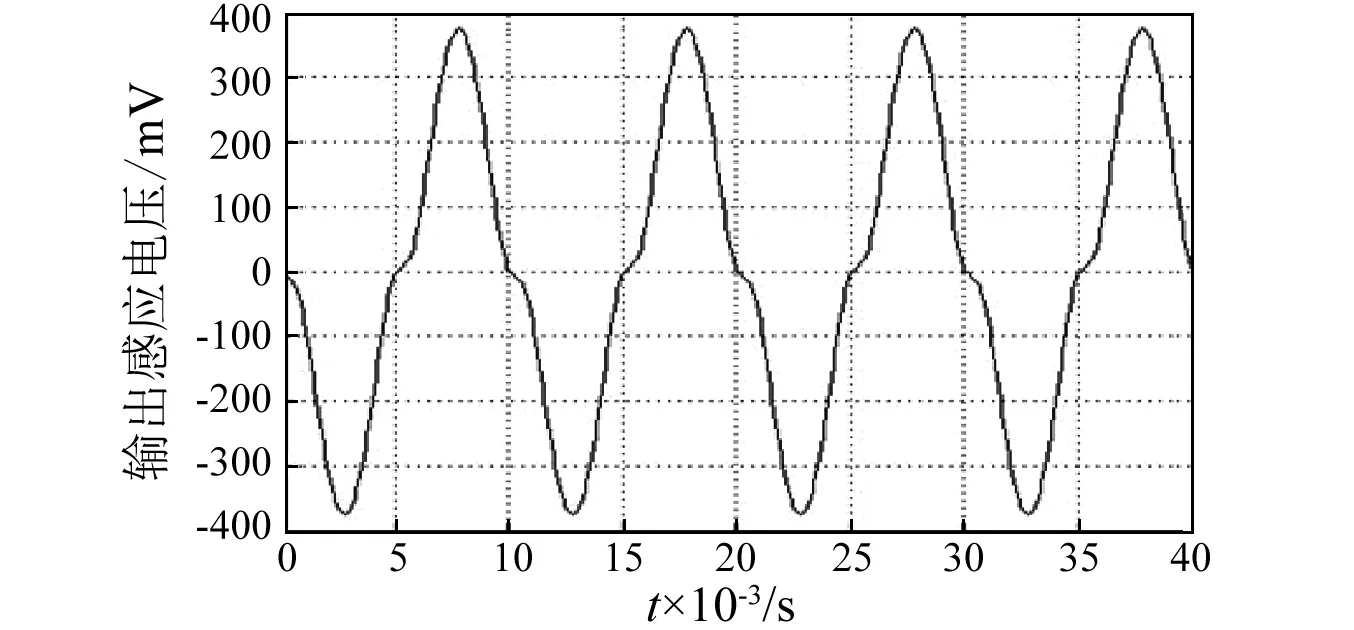
图2 正弦激振下的输出感应电动势Fig.2 The electromotive force of the device with the condition of sine excitation

2 柱棒式超磁致伸缩式振动能量收集装置

本文提出的一种柱棒式超磁致伸缩能量收集器的结构示意图，如图3所示。结构主要包括：超磁致伸缩棒、拾振机构、预应力施加装置、偏执磁场提供装置、感应线圈以及外壳等。其中，输入顶杆用于将模态激振器输出的激振信号传递到超磁致伸缩棒中，因此为了保证传递效率对其刚度要求较高，为了保证力传递的方向沿着超磁致伸缩棒的轴线方向并达到增大压应力的目的，将输入顶杆的一端设计成球面形状。碟簧和加压螺母主要是为超磁致伸缩棒提供预应力。为了改善超磁致伸缩棒的机电耦合关系以及提高能量转换效率，本设计在超磁致伸缩棒外部加了两块永磁体用来提供偏执磁场。力传感器安放于下底座内，与超磁致伸缩棒也为刚性接触。感应线圈缠绕在线圈骨架上，并通过底座壳体上的孔与外部的调节电路相连。

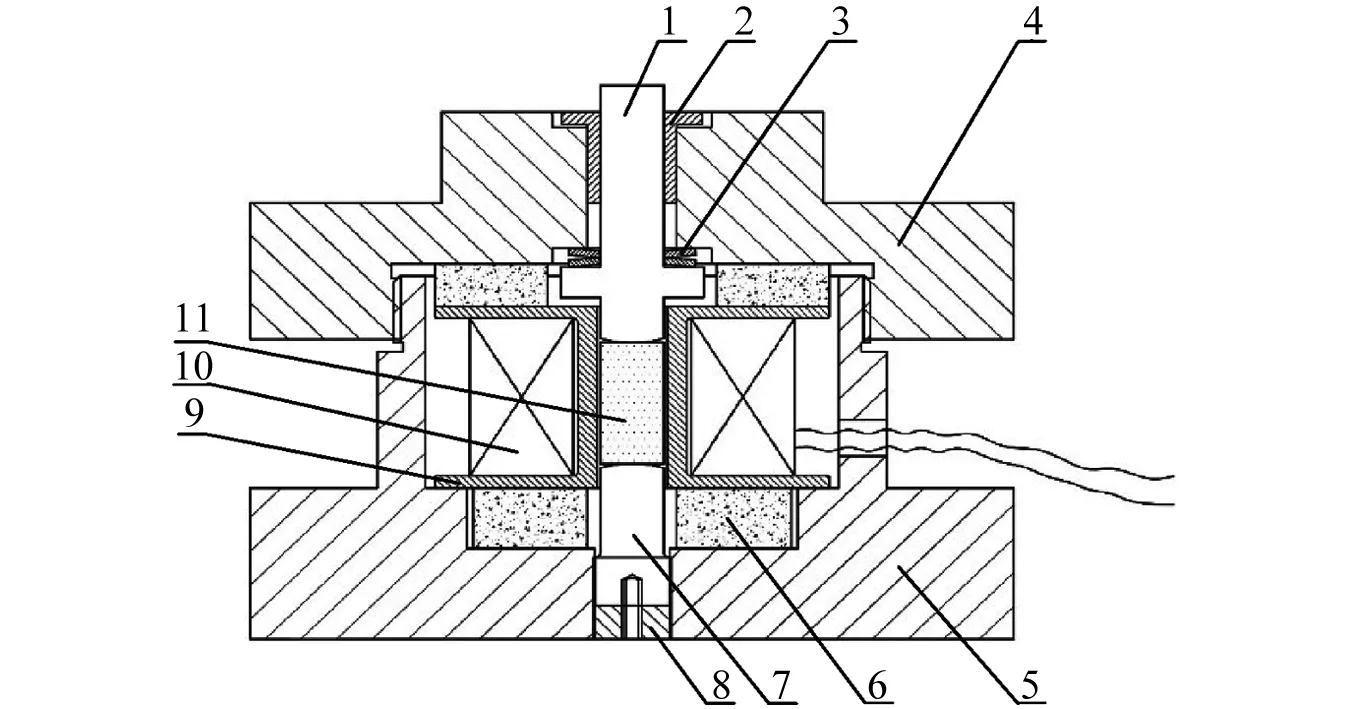
1.输入顶杆；2.自润滑铜套；3.蝶形弹簧；4.上端盖；5.底座；6.偏置永磁体；7.力传感器；8.防松螺钉；9.线圈骨架；10.感应线圈；11.超磁致伸缩棒图3 柱棒式超磁致伸缩式振动能量收集装置结构示意图Fig.3 Structure diagram of column giant magnetostrictive energy harvest device

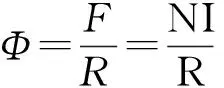
表1 振动能量收集装置中零部件材料Tab.1 The material of the parts of the vibrationenergy harvest device

表2 振动能量收集装置中重要部件的基本参数Tab.2 The basic parameters of important components of the vibration energy harvest device

3 实验验证

样机制作完成后，搭建实验平台，进行样机能量收集特性的验证工作。整个平台的测试原理图，如图4所示。首先，位移信号由信号发生器中设定好后通过功率放大器放大后输送到模态激振器中作为激振信号。然后，模态激振器的输出杆输出相应的位移激振并作用在样机的输入顶杆上，如果不考虑能量损失，间接地认为模态激振器的输出杆直接作用于超磁致伸缩棒上，使其产生周期性的变形。根据前文所述，在超磁致伸缩棒外部的感应线圈中会产生感应电动势。最后，通过能量回收电路将产生的电荷储存于电容中，并通过数字示波器将产生的电压信号显示并记录下来。通过比较理论值与实际测量值得相符程度来验证整个样机的能量收集的可靠性。

为了验证能量收集理论模型的仿真结果和样机实际输出值是否相符，实验采用的初始化参数与仿真相同即样机输入信号的幅值和频率分别设为100 N和100 Hz，用于提供激振信号的模态激振器的输出顶杆与样机的输入顶杆保持在一条直线上，并且对样机只施加正压应力。图5为实验测试平台，超磁致伸缩棒受到的激振应力，如图6所示。其最大值为2.54 MPa。

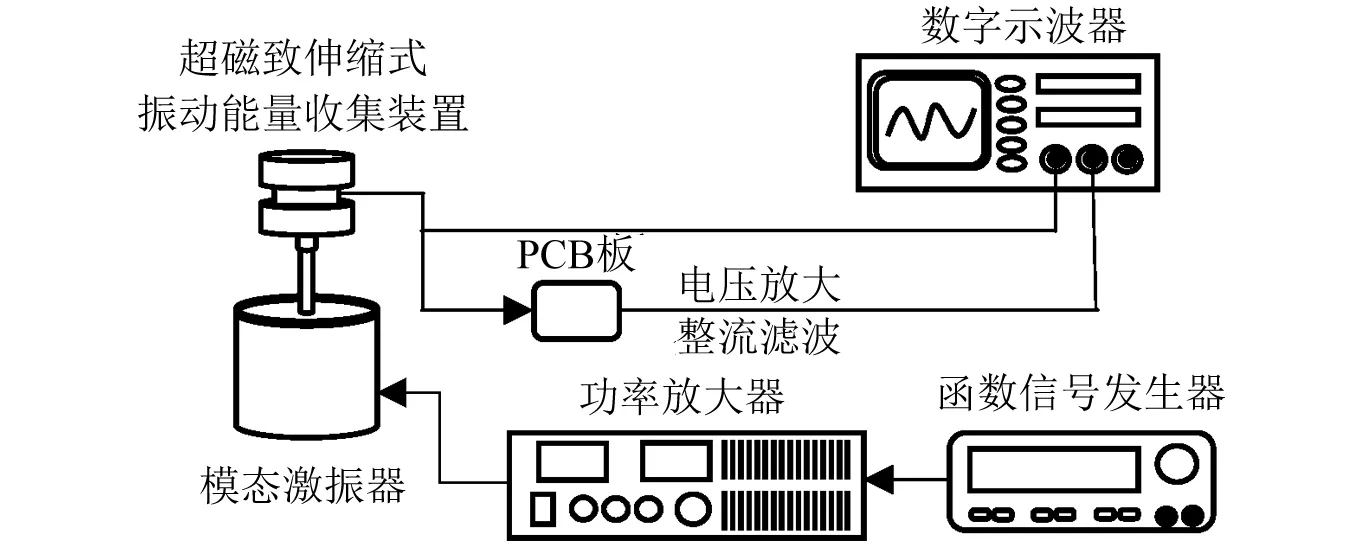
图4 样机实验测试原理图Fig.4 The principle diagram of the prototype test

图5 实验平台Fig.5 Experiment platform

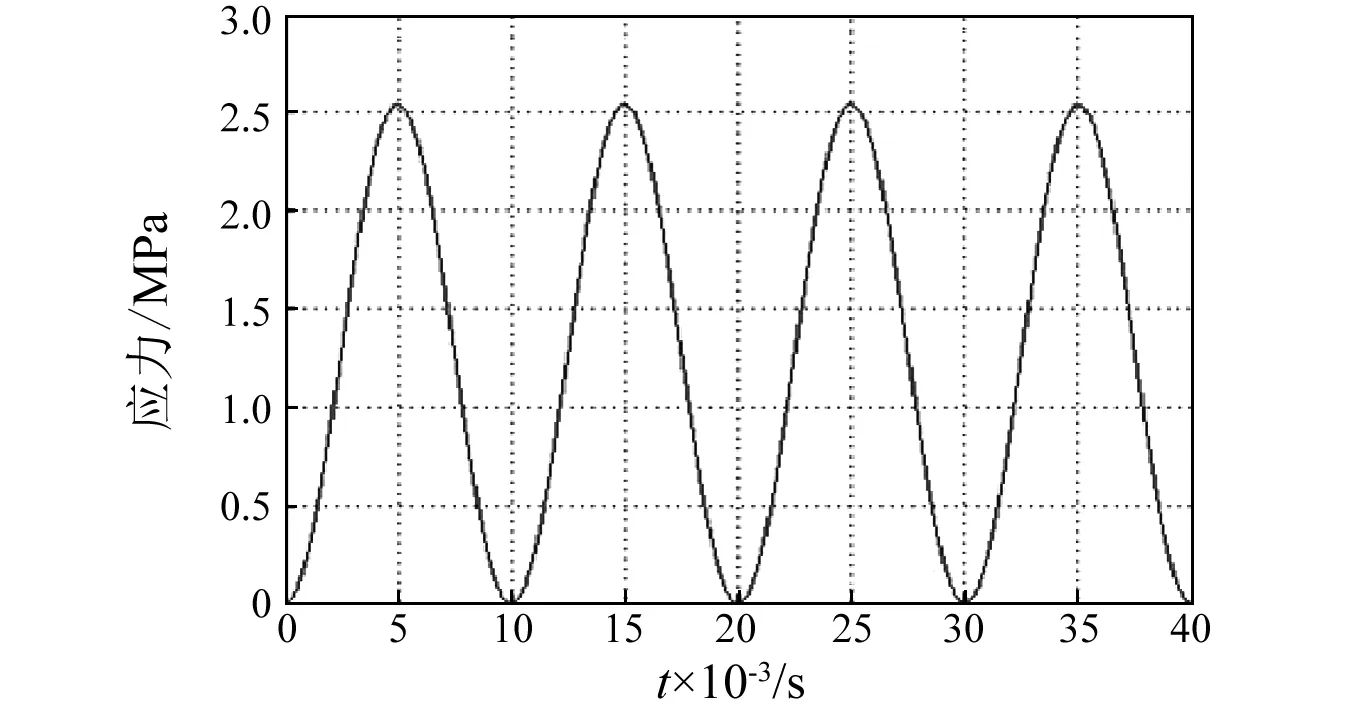
图6 激振器对超磁致伸缩棒施加的激振应力Fig.6 The excitation stress applied to GMM rod from vibration exciter

图7为模型仿真的理论输出感应电压和实验测的输出电压的对比曲线。

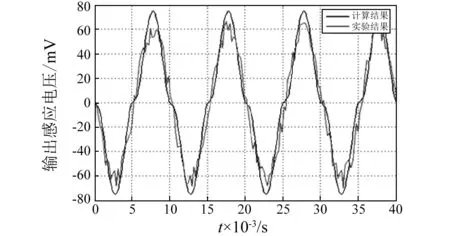
图7 理论计算输出感应电压和实验测的输出感应 电压的对比曲线Fig.7 The comparison curve of theoretical calculation output voltage and the experiment measuring output voltage

从图7可知，理论值和实验值的波形的变化规律基本一致，在激振幅值和激振频率分别为100 N和100 Hz时，实验测得的输出感应电压的峰峰值为136.4 mV，相应的仿真输出值为156 mV，实验值较理论值而言偏小，这是因为在理论计算时忽略了模态激振器输出顶杆与样机输入顶杆之间的能量损失，并且在仿真的过程中没有考虑磁漏对理论输出的影响。

为了得出所设计的能量收集装置的输出特性与激振信号的幅值和频率的关系，分别做了两组单因素实验即在幅值为定值30 N时，分别取激振频率为80 Hz、100 Hz、120 Hz得出相同振幅不同频率下振动能量收集装置输出的感应电压曲线，如图8所示。在频率为定值100 Hz时，分别取激振幅值为25 N、30 N、35 N得出不同振幅相同频率下振动能量收集装置输出的感应电压曲线，如图9所示。

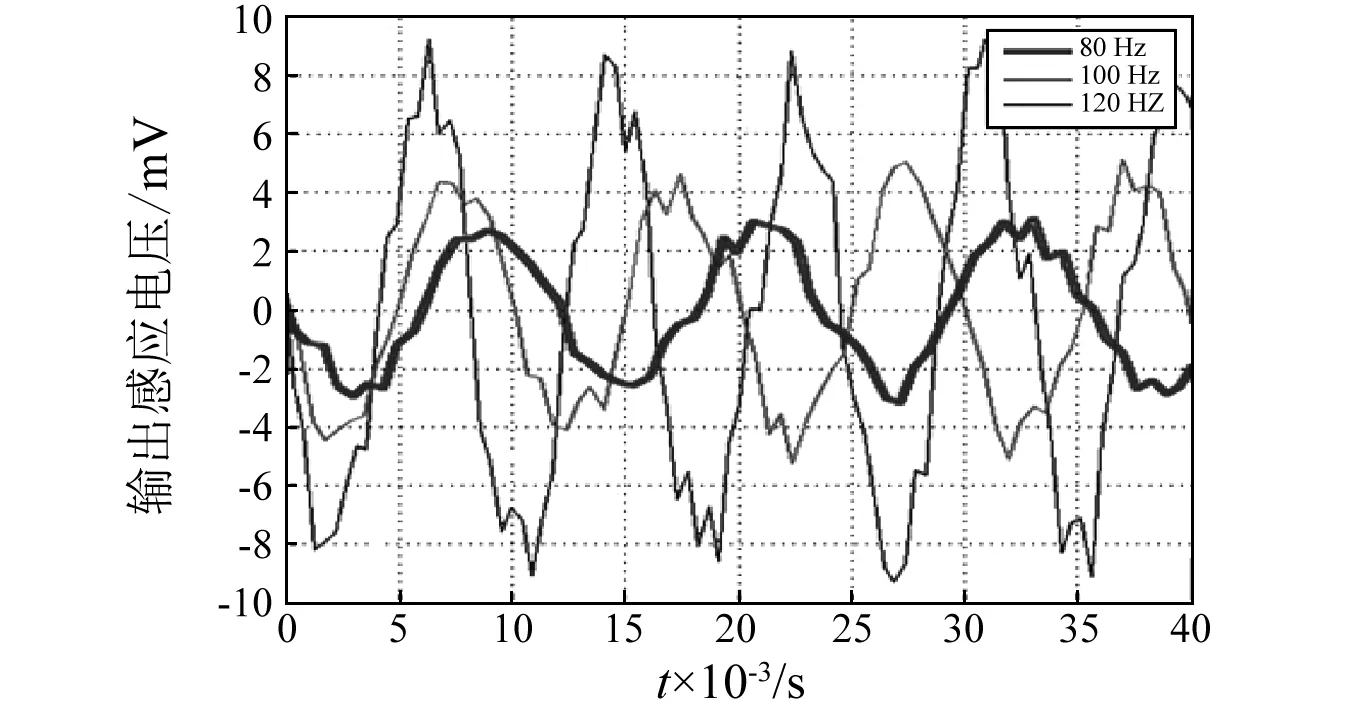
图8 相同振幅不同频率下振动能量收集装置输出的 感应电压曲线图Fig.8 The output voltage curve of the vibration energy harvest device at the same amplitude and under different frequency

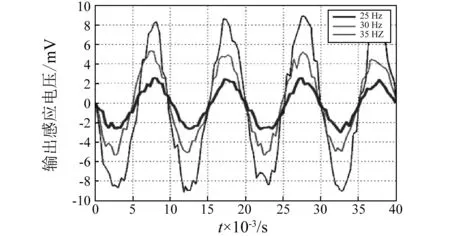
图9不同振幅相同频率下振动能量收集装置输出的 感应电压曲线图Fig.9 The output voltage curve of the vibration energy harvest device at the same frequency and under different amplitude

由图8和图9可知，本文设计的能量收集装置在相对较低激振幅值和激振频率下能够输出一定的电能。由输出特性曲线图可知，在激振频率fn不变时，能量收集装置的输出感应电压的峰峰值与激振幅值Fm成正比；反之，在激振幅值Fm不变时，能量收集装置的输出感应电压的峰峰值与激振频率fn成正比。因此，通过实验得出的装置的输出特性与仿真得出的输出特性基本相符，从而进一步验证了理论模型的正确性，同时也可以验证实验设计的可靠性。输出电压峰峰值与激振频率和激振幅值的非线性主要是由于以下几个因素产生的：①激振器自身的非线性；②温度的变化对实验结果的影响；③实验系统的检测精度的影响。

4 结 论

本文根据目前振动能量收集技术的现状，基于对超磁致伸缩材料物理特性的分析，设计了一套柱棒式振动能量收集装置。仿真结果表明了本文建立数学模型的正确性，并通过实验得出在频率为100 Hz、大小为100 N的正弦应力输入信号的条件下，样机输出感应电动势峰-峰值136.4 mV，接近仿真计算值(156 mV)，且波形基本一致，验证了实验设计的可靠性。基于实验结果得出本文提出的柱棒式超磁致伸缩能量收集装置在较小应力和较低频率的振动激励条件下能够输出一定的电能，因此，在实际工程环境下利用文中提出的能量收集装置进行能量收集是可行。

[1] 孙明慧. 磁致伸缩换能器的结构设计和磁场分析及实验研究[D]. 天津: 河北工业大学, 2014.

[2] 侯志伟，陈仁文，刘祥建．多方向压电振动能量收集装置及其优化设计[J]．振动与冲击, 2012,31(16): 33-37. HOU Zhiwei, CHEN Renwen, LIU Xiangjian. Optimization design of multi-direction piezoelectric vibration energy harvester [J]. Journal of Vibration and Shock, 2012,31(16): 33-37.

[3] 王博文，曹淑瑛，黄文美．磁致伸缩材料与器件[M]．北京：冶金工业出版社, 2008.

[4] ADLY A, DAVINO D, GIUSTINIANI A, et al. Experimental tests of a magnetostrictive energy harvesting device toward its modeling[J]. Journal of Applied Physics, 2010, 107(9):09A935.

[5] UENO T. Performance of improved magnetostrictive vibrational power generator, simple and high power output for practical applications[J]. Journal of Applied Physics, 2015, 117(17): 1416-1421.

[6] FUJIEDA S, SUZUKI S, MINATO A, et al. Growth of Fe-Ga alloy single crystals by the czochralski method and their application to vibration power generator[J]. IEEE Transactions on Magnetics, 2014, 50(11):1-4.

[7] UENO T, YAMADA S. Performance of energy harvester using iron-gallium alloy in free vibration[J]. Magnetics IEEE Transactions on, 2011, 47(10):2407-2409.

[8] 郭岩. 基于磁致伸缩材料的振动能量采集研究[D].天津: 河北工业大学, 2014.

[9] WANG L, YUAN F G. Vibration energy harvesting by magnetostrictive material[J]. Smart Materials and Structures, 2008, 17(4):1-14.

[10] JILES D C. Theory of the magnetomechanical effect[J]. Journal of Applied Physics, 1995, 28(8): 1537-1546.

[11] JILES D C, THOELKE J B, DEVINE M K. Numerical determination of hysteresis parameters for the modeling of magnetic properties using the theory of ferromagnetic hysteresis[J]. IEEE Trans on Mag, 1992, 28(1):27-35.

[12] DONG S X, LI J F, VIEHLAND D. Longitudinal and transverse magnetoelectric voltage coefficients of magnetostrictive/piezoelectric laminate composite: theory [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2003, 50(10): 1253-1261.

Design and experiments of a column giant magnetostrictive energy harvester

MENG Aihua, YANG Jianfeng, JIANG Sunquan, LIU Fan, LIU Chenglong

(College of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, China)

In order to make use of the vibration energy from nature and power micro devices, a kind of vibration energy harvester based on giant magnetostrictive material (GMM) was designed and verified through an experiment. First, based on the analysis of the physical properties of GMM, the modeling and simulation of the energy harvest device has been analyzed. And then, according to the results of simulation analysis, a set of columnclaviform giant magnetostrictive energy harvester was designed. Finally, an experimental platform was established to verify the effect of the design. Experimental results indicate that when the frequency of input excitation signalfnis constant, the peak-to-peak value of the output voltage of the device is directly proportional to the amplitude of input vibration signalFm. When the amplitude of input vibration signalFmis constant, the peak-to-peak value of the output voltage of the device is directly proportional to the frequency of the input excitation signalfn. When the maximum of the vibration stress is 2.54 MPa, the sinusoidal vibration frequency is 100 Hz and the turns of induction coil is 100, the peak-to-peak value of output electromotive force of the device is 136.4 mV. This result is better in line with the theoretical value (156 mV) and the waveform is consistent as well.

vibration; energy harvester; giant magnetostrictive material

国家自然科学基金资助项目( 50905051；11202061)；浙江省自然科学基金(LY17E050026)

2016-01-21 修改稿收到日期： 2016-03-25

孟爱华 女，博士，副教授，1978年生

TK02

A

10.13465/j.cnki.jvs.2017.12.029