基于相关向量机模型的设备运行可靠性预测

冯鹏飞, 朱永生, 王培功, 闫 柯

(西安交通大学 现代设计及转子轴承系统教育部重点实验室,西安 710049)

基于相关向量机模型的设备运行可靠性预测

冯鹏飞, 朱永生, 王培功, 闫 柯

(西安交通大学 现代设计及转子轴承系统教育部重点实验室,西安 710049)

针对机械设备失效数据少、传统基于统计的可靠性评估方法不能有效评估设备可靠性的问题，引入运行可靠度的概念来描述设备运行状态，并提出了一种基于相关向量机的设备运行可靠性预测方法。该方法首先采用运行可靠性计算模型，建立特定特征指标与运行可靠性的关系；然后采用相关向量机预测不同时刻下特征指标的值及其概率密度函数，并将其输入到运行可靠性模型，计算获得其所对应的运行可靠度。将该方法应用到航空发动机转子轴承运行可靠性分析中，预测的轴承失效时间与实际失效时间误差<5%，证明该方法的有效性和合理性。

运行可靠性；相关向量机；可靠性预测；状态信息

可靠度是指产品在规定条件、规定时间内，完成规定功能的概率[1]。如何评价机械设备的可靠度并预测设备的失效时间，对设备的运行和维护具有重要的意义。常用的可靠度预测方法主要有两种：一种是基于设备失效寿命统计数据的传统可靠性预测方法，但对于目前大多数机械设备来说，获得其失效寿命数据比较困难。因此，传统可靠性预测方法对于此类设备具有较大的局限性；另外一种是基于设备状态信息的可靠性预测方法。设备的退化状态数据在可靠性评价和剩余寿命预测上比失效数据能提供更多的信息[2]。所以，根据设备的状态信息对设备的运行可靠性进行评估和预测具有重要的意义。

基于状态信息的可靠性预测方法一般首先根据设备的特征指标对设备可靠度进行评估，然后基于各种预测算法对可靠度进行预测。方明杰等[3]以数控珩磨机液压系统为例，利用KM理论对液压系统的可靠度进行评估，提出了一种基于支持向量机的可靠性评估方法。Lu等[4]利用时间序列模型，分析了钻孔机运行可靠度在不同时刻的变化。陈保家等[5]利用人工神经网络模型，选取刀具加工过程中的磨损量作为模型输入，以利用Bayes和Kaplan-Meier理论计算得出的运行可靠度作为模型输出，较为准确地预测了设备的失效时间。在上述流程中，如何评估设备的可靠度是首先需要解决的问题。常见的处理方法是采用KM评估器，通过计算未失效样本数目与全部样本数目的比值来近似计算运行可靠度，但在样本数量比较稀少时，该方法仍然可能带来较大的偏差。

相关向量机(Relevance Vector Machine， RVM)是由Tipping[6]提出的基于贝叶斯理论的机器学习方法。与支持向量机相比，它不仅有处理小样本问题时相似的运算精度，同时还能提供概率式的预测，通过与可靠度计算模型相结合可以较好地解决计算偏差的问题。因此，本文提出了一种基于相关向量机的设备运行状态可靠性预测方法。该方法选取设备的运行状态特征指标作为模型输入，利用相关向量机模型预测得出某一时刻该特征指标的后验分布函数，根据设定的失效阈值，由失效阈值与指标预测值的区间积分的比值来计算该时刻下的运行可靠度。本文通过对航空发动机转子轴承失效时间的正确预测实例，证明该评估方法的有效性和正确性。

1 相关向量机回归预测模型

ti=y(xi,ω)+εi

(1)

式中：xi为输入向量；ti为目标值；样本噪声εi服从均值为0，方差为σ2的高斯分布，即εi·(0,σ2)。相关向量机的输出模型可以表示为：

(2)

式中：ωi为模型的权重值；K(x,xi)为模型的核函数。则相应的训练样本集的似然函数为：

p(t|ω,σ2)=

(3)

式中：t=(t1,…,tN)T，ω=(ω1,…,ωN)T，Φ=[φ(x1),φ(x2),…,φ(xN)]T为N×(N+1)设计矩阵，且φ(xi)=[1,K(xi,x1),K(xi,x2),…,K(xi,xN)]T，i=1,2,…，N。为了避免产生过学习问题，对每一个权重系数ωi引入超参数αi。假设ωi服从均值为0，方差为α-1的高斯分布，则有：

(4)

根据贝叶斯公式，利用定义的似然函数式(3)和先验分布函数式(4)，可以得到权值ω的后验分布函数。 即：

(5)

p(ω|t,ασ2)=N(ω|μ,Σ)

(6)

后验协方差和均值分别为：

Σ=(σ2ΦTΦ+A)-1

(7)

μ=σ-2ΣΦTt

(8)

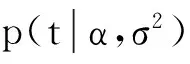
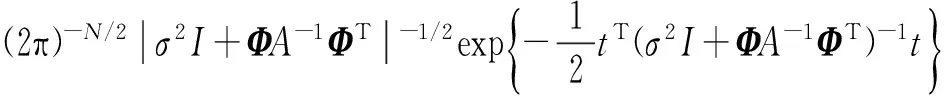
(9)

对α,σ分别求偏导并令其导数式为0[7]，得出以下迭代公式：

(10)

(11)

(12)

又式(12)服从高斯分布，即

(13)

式中，预测均值和方程分别为：

y*=μTφ(x*);

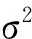
2 运行可靠度预测模型的建立

在传统可靠性理论中，根据可靠度的定义，可靠度的评估方法被定义为：

(14)

式中：T为设备的寿命；t为规定的使用时间；f(t)为T的概率密度函数。

传统可靠性理论有两个缺点：①设备运行状态信息的变化并没有体现出来，在设备退化过程中的状态信息可以用来预测可靠度；②传统可靠性理论只能提供设备的整体可靠度[9]，但人们更关心的是具体设备运行中的可靠度的变化。针对此问题，文献[10]提出先估计出单一设备状态特征指标在不同时刻的PDF，然后由失效阈值和指标观测值所界定的区间积分来计算相应的运行可靠度。其原理如下：

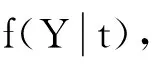
(15)

那么设备i在t+kΔt时刻的可靠度为：

Ri(t+kΔt)=

上述方法需要选择特征值的PDF分布形式，并对PDF进行估计。但当设备接近失效时，如果样本数较少，所估计的模型参数误差就很大，会影响预测的准确性。考虑到相关向量机不仅有近似支持向量机的准确率，同时还能获得预测值的概率输出。因此，本文将相关向量机与可靠度计算模型结合起来，利用相关向量机回归模型训练得出特征指标在不同时刻的后验分布函数，根据特征指标的预测值和设定阈值所定义的区间积分来即可计算出该时刻下的运行可靠度，较好地解决该可靠度计算方法应用困难的问题，同时避免了较大的计算偏差。其可靠性预测流程，如图1所示。

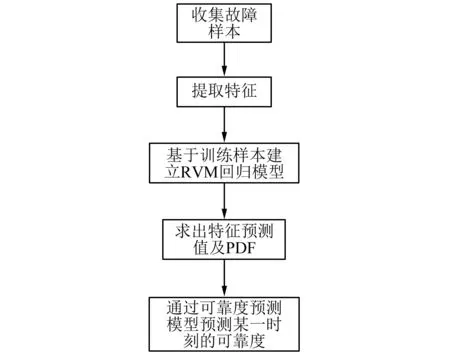
图1 基于RVM模型的可靠性预测流程Fig.1 Reliability prediction process based on RVM model

3 航空发动机转子轴承可靠性预测

3.1 试验数据的获取

本文采用的数据来自于美国辛辛那提大学智能维护中心(NSF I/UCR Center on Intelligent Mataintenance Systems(IMS))实验得出的航空发动机转子轴承疲劳寿命实验数据，其试验台结构，如图2所示。该试验台由交流电机驱动，利用带传动带动试验台主轴旋转，可同时对四个航空发动机转子主轴轴承进行疲劳寿命实验。实验过程中，利用PCB353B33高灵敏度ICP振动加速度传感器采集每个轴承水平和竖直两个方向的振动加速度信号，数据记录间隔为10 min。所有轴承采用油液润滑，在回油管上装有磁塞，监测铁屑含量，超过设定临界值时则自动切断电路。本文选取的是一组采样长度为984个点的1#轴承失效数据，采样时间为9 840 min。

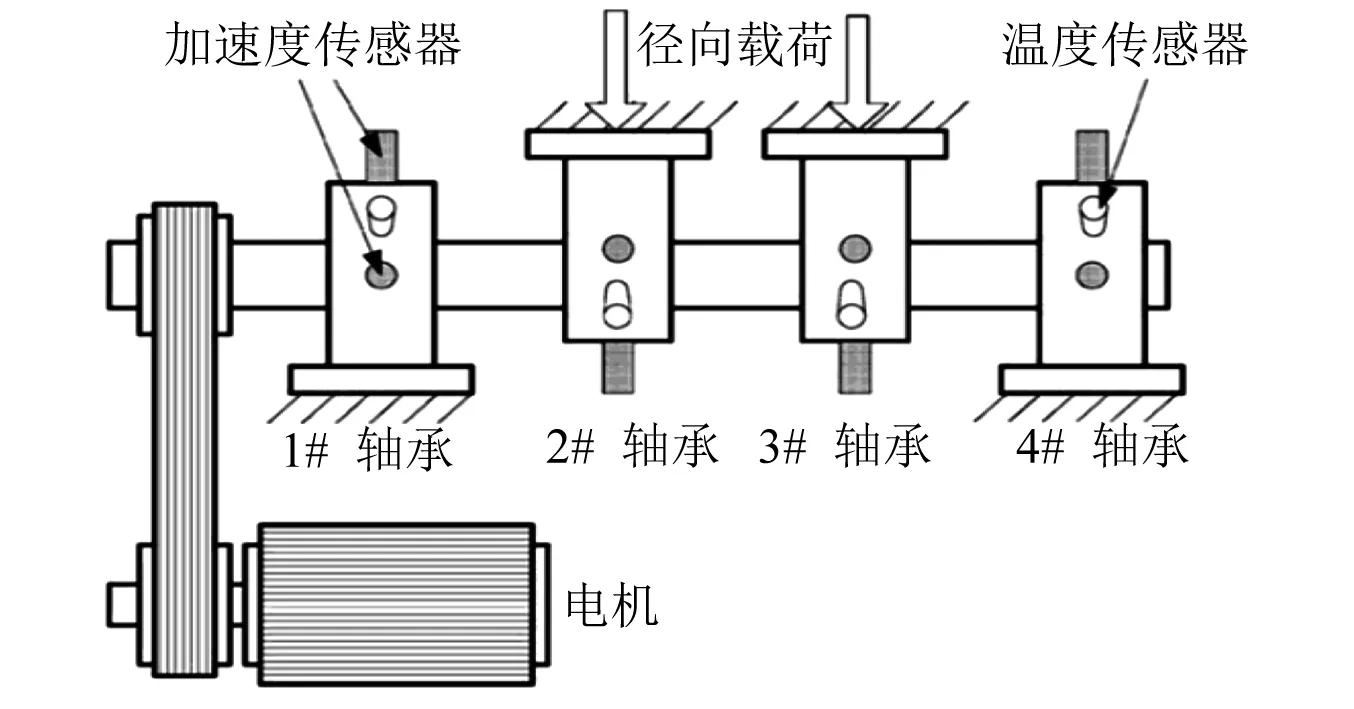
图2 轴承试验台及传感器布置图Fig.2 Bearing test bed and sensor arrangement

为了实时掌握轴承的运行状况，需要提取能够反映轴承运行状态的特征指标。信号的时域统计量计算简单、快捷，并且对滚动轴承的缺陷足够敏感，能够较好地反映出滚动轴承故障的存在，常用于在线监测。其中，有量纲时域参数依赖于历史数据并对载荷和转速等变化比较敏感，而无量纲时域参数指标基本不受载荷和转速等因素影响，无需考虑相对标准值或与以前的数据进行对比。由图3可知，波形指标在轴承正常运转时波动较小，随着轴承进入早期损伤阶段，其值有明显增大，随着损伤的扩展，幅值又进一步增。当轴承失效时，其值剧烈增加到最大。同时，波形指标的敏感性和趋势性都较好，因此，本文选用波形指标作为反映轴承运动状态的特征指标[11]，波形指标的计算公式，如式(17)所示。定义的波性指标失效阈值为1.30，可以得到轴承第一次开始发生失效的点为第703个采样时间点，此时刻为t=7 030 min。

(17)

图3 轴承波形指标变化趋势Fig.3 The change trend bearing waveform index

3.2 可靠性建模及预测

在确定特征指标和阈值后，本文选取轴承失效数据中前6 500 min的状态信息(即前650个点)作为训练样本，构建其特征指标的单步预测模型。模型嵌入维数为20，即以当前时间点及其前面19个特征值作为模型输入，预测其下一步特征值。RVM对特征值单步预测的结果，如图4所示。可见RVM具有良好的泛化能力，其预测值的与实际值接近。同时，基于RVM预测的每一采样时刻特征值的后验概率分布，由式(16)计算出的可靠度曲线，如图5所示。由图5可知，当轴承运行到t=7 190 min时，其瞬时可靠度≈0，可以认为失效。由图3可知，样本开始发生失效的点为t=7 030 min的采样时间点，因此，预测失效点与实际失效点误差<5%，证明本文方法可以较为准确预测出轴承的失效时间。

图4 波形指标预测的变化趋势Fig.4 The prediction waveform index

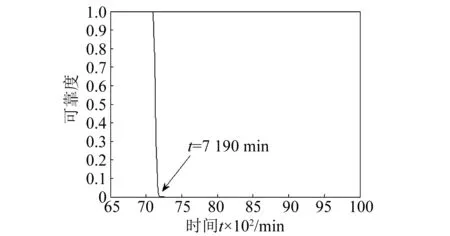
图5 轴承的可靠度预测曲线Fig.5 Reliability prediction curve of bearing

同样的，该方法也适用于轴承其它特征指标的评价。考虑到峰值、峭度指标也是轴承运动状态的重要指标，本文分别从实验数据中提取出峰值指标和峭度指标，采用以上提出的方法建立可靠度预测模型，预测结果，如表1所示。由表1可知，当选择其它特征指标时，基于相关向量机模型的可靠度预测方法依然能够较好预测轴承的运行状态，证明了该方法的有效性。

表1 特征值预测结果Tab.1 The prediction of characteristic value

另外，文献[12]以采用基于比例协变量模型的Logistic回归求得1#轴承的运行可靠度曲线，预测的轴承失效的时间点为t=770，与实际故障发生时间点t=703相比误差为9.5%，进一步证明了基于相关向量机的可靠度预测方法的可行性。

4 结 论

本文提出了一种基于相关向量机模型的运行可靠性预测方法。通过对转子轴承运行可靠性的分析和预测，得出以下结论：

(1)相关向量机模型可以实现概率式的预测。即不仅可以提供较高精度的预测值，还可以得到预测值的概率密度函数；

(2)相关向量机的训练是在贝叶斯框架内进行的，虽然相比支持向量机，其核函数的计算量较少，但其训练时间较长；

(3)基于预测值概率分布区间积分比值的可靠度模型可以较好地预测轴承的可靠度，实时预测评估轴承的运行状态；

(4)以实例说明基于相关向量机模型的状态可靠性预测方法可以正确地预测轴承的失效时间，证明了该方法的有效性。

[1] 额田启三.机械可靠性与故障分析[M].北京：国防工业出版社，2006.

[2] GORJIAN N, MA L, MITTINTY M, et al. A review on degradation models in reliability analysis[M]∥ Engineering Asset Lifecycle Management. London: Springer, 2010.

[3] 方明杰, 周光辉, 程元森,等. 基于运行状态信息的数控珩磨机液压系统可靠性预测方法[J]. 应用科技, 2012,39:30-33. FANG Mingjie, ZHOU Guanghui, CHENG Yuansen, et al.

Reliability prediction for hydraulic system of CNC honing machine based on the operational status information[J]. Applied Science and Technology,2012,39:30-33.

[4] LU H, KOLARIK W J, LU H. Real-time performance reliability prediction[J]. IEEE Transactions on Reliability, 2002, 50(4):353-357.

[5] 陈保家, 陈雪峰, 何正嘉,等. 利用运行状态信息的机床刀具可靠性预测方法[J]. 西安交通大學學報, 2010, 44(9):74-77. CHEN Baojia, CHEN Xuefeng, HE Zhengjia, et al. Operating condition information—Based reliability prediction of cutting tool[J]. Journal of Xi’an Jiaotong University,2010,44(9):74-77.

[6] TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1(3):211-244.

[7] 曲晓燕, 范庚, 马登武. 基于相关向量机的导弹贮存可靠性预测方法研究[J]. 计算机测量与控制, 2013, 21(11):3021-3022. QU Xiaoyan, FAN Geng, MA Dengwu. Study on storage reliability prediction of missiles based on relevance vector machine[J]. Computer Measurement & Control, 2013, 21(11):3021-3022.

[8] 赵金晶, 李松娜. 基于相关向量机的股指数预测及其置信区间[J]. 四川教育学院学报, 2007, 23:104-106. ZHAO Jinjing, LI Songna. The relevance vector machine based stock market index forecasting and confidence interval[J]. Journal of Sichuan College of Education, 2007, 23: 104-106.

[9] HENG A, ZHANG S, TAN A C C, et al. Rotating machinery prognostics: state of the art, challenges and opportunities[J]. Mechanical Systems & Signal Processing, 2009, 23(3):724-739.

[10] AIWINA H, ANAY C C T, JOSEPH M, et al. Intelligent condition-based prediction of machinery reliability[J].Mechanical Systems & Signal Processing, 2009, 23(5):1600-1614.

[11] 陈玉. 基于状态信息的机械设备运行可靠性评估方法研究[D].西安：西安交通大学，2014.

[12] 陈保家. 基于设备运行状态的可靠性评估技术及应用研究[D].西安交通大学，2011.

Operational reliability prediction of equipment based on relevance vector machine

FENG Pengfei, ZHU Yongsheng, WANG Peigong, YAN Ke

(Key Laboratory of Education Ministry for Modern Design and Rotor-Bearing System, Xi’an Jiaotong University, Xi’an 710049, China)

Due to lack of failure data, traditional statistics-based reliability evaluation methods cannot effectively evaluate the reliability of mechanical equipment. The operational reliability concept was introduced in this work to describe the running condition of the equipment, and a prediction method for the operational reliability based on relevance vector machine (RVM) was proposed. In the method, the operational reliability calculation model was adopted firstly to establish the relationship between status indicators of the equipment and the operational reliability, and then the relevance vector machine was introduced to predict the trend and the corresponding probability distribution function (PDF) of the status indicators. Finally, the predicted values and PDF of status indicators were inputted into the operational reliability calculation model and the predicted operational reliability of the equipment was then obtained. The method was applied to the operational reliability evaluation of aero engine bearings, the result show that the error between the predicted failure time and the actual failure time was within 5%, which proves the rationality and effectiveness of the method.

operational reliability； relevance vector machine；reliability forecasting； operating information

国家自然科学基金资助项目(51275383)；国家重大科技专项(2012ZX04005-011)

2016-01-08 修改稿收到日期： 2016-04-19

冯鹏飞 男，硕士生，1991年生

朱永生 男，教授，博士生导师，1973年生

TH17

A

10.13465/j.cnki.jvs.2017.12.024