基于混沌模拟退火PSO算法的威布尔分布参数估计应用研究

许 伟, 程 刚, 黄 林, 位秀雷, 瓮 雷

(海军工程大学 动力工程学院，武汉 430033)

基于混沌模拟退火PSO算法的威布尔分布参数估计应用研究

许 伟, 程 刚, 黄 林, 位秀雷, 瓮 雷

(海军工程大学 动力工程学院，武汉 430033)

针对三参数威布尔分布模型采用精确解法直接求解的不足，提出基于混沌模拟退火粒子群优化方法进行参数估计。引入Logistic混沌因子调整粒子群优化算法的更新策略以充分释放其遍历搜索能力，并采用模拟退火方法依据Tsallis接受准则以一定概率接受新状态，使算法避免陷入“早熟”进而实现全局最优搜索；同时为降低算法在迭代计算上的时间开销，运用图解法获得的初始解为其提供搜索范围。将该方法运用到轴承转子可靠度威布尔分布参数估计中，实验分析表明该方法具有可行性和有效性，与遗传算法、模拟退火粒子群优化算法相比具有更好的寻优能力。

混沌；模拟退火；粒子群算法；威布尔分布；参数估计

可靠性分析是产品使用过程中的一项重要工作，发挥着越来越重要的作用，威布尔分布作为一种描述机械寿命分布的概率统计模型以其强大的适应性和鲁棒性正被广泛应用。两参数威布尔分布在描述设备初期可靠性时误差较大，而三参数威布尔分布能够准确描述产品全寿命周期可靠性分布规律，但相应的复杂性也更高[1-2]。针对三参数威布尔分布的参数估计求解目前主要的方法有图解法、线性回归估计法、极大似然估计法、Bayes估计法、距估计法、最速下降法[3-5]等。图解法根据已知数据结果通过绘制概率图计算三个参数，优点在于计算简单，使用方便，但参数估计结果误差较大；杨志忠等[6]采用最小二乘法进行线性回归求得形状参数，再结合插值法得出尺度参数和位置参数，求解过程相当复杂；杨谋存等[7]将降阶法和二分法结合起来去解极大似然法的三个非线性的超越方程组，计算复杂繁琐，对初值要求较高；潘晓春[8]用概率权重距法以含幂次的概率作为权重乘以随机变量来计算分布参数，该方法对于子样较少的分布计算精度不足，且依赖经验拟合。

粒子群算法(Particle Swarm Optimization, PSO)是由Kennedy等于1995年提出的一种模拟鸟群觅食行为的智能计算方法[9-10]，以其模型简单、算法易于实现、收敛速度快的优势引起许多学者的关注，并广泛运用于威布尔分布参数估计中。罗航等[11]将双线性回归估计法和极大似然估计法结合起来求出初值，再运用PSO算法进行优化得出最优解。王琼等[12]将模拟退火方法融入到粒子群优化算法中进行威布尔分布参数估计。刘爱军等[13]通过理论研究分析得出混沌模拟退火粒子优化算法是一种优化能力、效率和可靠性均较高的全局优化方法。

本文将PSO算法应用于三参数威布尔分布参数估计中，针对标准PSO算法优化结果容易造成局部最优产生“早熟”现象的缺点，引入Logistic混沌因子调整粒子群优化算法的更新策略和模拟退火的降温策略形成混沌模拟退火PSO算法，同时为减少算法计算时长采用图解法得出的参数估计的粗略结果为混沌模拟退火PSO算法提供搜索范围以得到更精确的参数估计值。实验采用多功能转子模块实验台为研究对象进行应用研究，结果表明该方法具有可行性和有效性,在对其它方法进行的比较分析得出该方法具有更好的优化能力。

1 改进混沌模拟退火粒子群优化算法

1.1 标准PSO算法的描述

PSO算法是通过初始值的不断更新迭代搜寻局部最优解pbest和全局最优解gbest来实时调整自己的下一时刻位置和速度最终完成寻优。

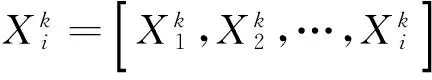
(1)

式中：ω为惯性权重系数；控制粒子速度更新，使粒子具有扩展搜索空间的趋势，当ω较大时全局搜索能力较强，当ω较小时局部搜索能力较强；c1为局部学习因子；c2为全局学习因子；r1和r2为[0,1]之间的独立随机数。

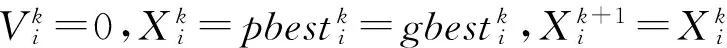
1.2 基于混沌序列的粒子群参数更新策略

为充分释放粒子群算法的遍历搜索能力，利用混沌序列的遍历性与对初值的敏感性，引入Logistic混沌因子

(2)

1.2.1 混沌局部加速因子更新

(3)

式中：δ为步长因子；Nt为t时刻粒子数。

1.2.2 混沌全局加速因子更新

(4)

1.2.3 混沌惯性权重因子更新

惯性权重系数具有平衡局部最优值和全局最优值的能力，较大时粒子具有较强的全局搜索能力；较小时具有较强的局部搜索能力，更新公式如下：

(5)

1.3 混沌模拟退火粒子群优化算法过程

模拟退火算法的思想是模拟固体由高温逐渐冷却到低温最终实现热平衡的过程，采用一定的接受准则不断反复迭代寻找能量达到最小点的状态值。

1.3.1 Tsallis接受准则

王琼等采用Metroplis接受准则，缺点在于局部退火速度慢，本文使用Canchy-Lorentz迁移分布和Tsallis接受准则，局部退火速度快、效率高。

Canchy-Lorentz迁移分布：

(6)

式中：Δx是变量x的试探迁移距离；D是常数。

Tsallis接受准则[15]：

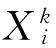
(7)

1.3.2 模拟退火算法降温策略

(8)

(9)

(10)

式中：α为显著性水平；Uα由正态分布数值表得到

(11)

由式(11)得出的限定区域大大缩小了搜索区域，同时在缩小的区域上不断反复迭代，降温速率显著加快，寻优效率得到提高。

1.3.3 混沌模拟退火粒子群优化算法

混沌模拟退火粒子群优化算法过程，如图1所示。

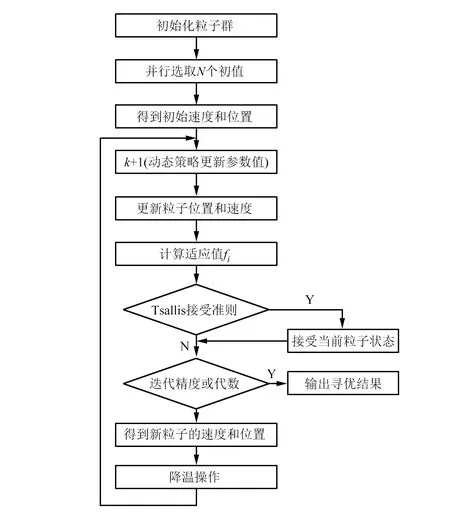
图1 混沌模拟退火粒子群优化算法流程Fig.1 Chaotic simulated annealing particle swarm optimization algorithm process

2 三参数威布尔分布及参数估计方法

2.1 三参数威布尔分布

若机械零部件寿命t服从三参数威布尔分布，则其概率密度函数为：

(12)

累积失效概率函数为：

(13)

可靠度函数为：

(14)

式中：β>0为形状参数；η>0为尺度参数；γ≥0为位置参数[16]。

2.2 图解法参数估计

图解法参数估计是通过威布尔概率图(Weibull Probability Plot，WPP)计算得到。对式(14)左右两边取两次自然对数，则有：

ln{-ln[R(t)]}=βln(t-γ)-βln(η)

(15)

对式(15)作威布尔变换，令

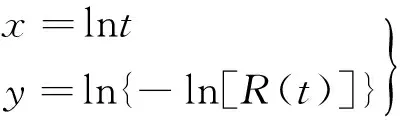
(16)

根据式(15)的性质，当t-γ=0，即x=lnγ时，y趋向于-∞，当t趋向于+∞时，y=βx-βln(η)。因此x=lnγ和y=βx-βln(η)是式(15)经过威布尔变换后得到的两条渐近线。通过作WPP图可计算出β,η,γ的估计值。WPP图解法的一般步骤如下：

步骤1 将ti=(i=1,2,…,n)的观测值按由小到大的顺序进行排列。

(17)

式中：n为样本大小。

步骤4 在WPP图中拟合两条渐近线：一条位于所有散点的左侧垂直x于轴，表达式为x=x0；另一条是在x趋向于+∞时的渐近线，其图形近似直线，表达式为y=ax-b。

因此可求出：

(18)

2.3 混沌模拟退火PSO算法优化问题描述

采用PSO优化威布尔分布参数估计，目标函数为

(19)

以图解法求得的初始位置作为初始种群根据本文提出的混沌模拟退火粒子群优化算法流程进行求解。

3 实例分析

汽轮机轴承转子是机械中常用部件，在运行过程中易发生疲劳损伤和磨损，因此其可靠性对于设备的安全运行至关重要。图2是设计的多功能轴承转子实验平台。

实验台转子转速为2 700 r/min，采样频率为10 kHz，当轴承出现横向裂纹时，转子会出现扭振现象，扭振信息以相位调制的形式存在于轴承的振动信号中形成调相信号。相位调制在时频图上表现为信号的频率调制，并且频率和转子频率相同，利用该特征可判断轴承裂纹故障，进而可得出轴承失效时间。

图2 多功能轴承转子实验平台Fig.2 Multi-function rotor experiment platform

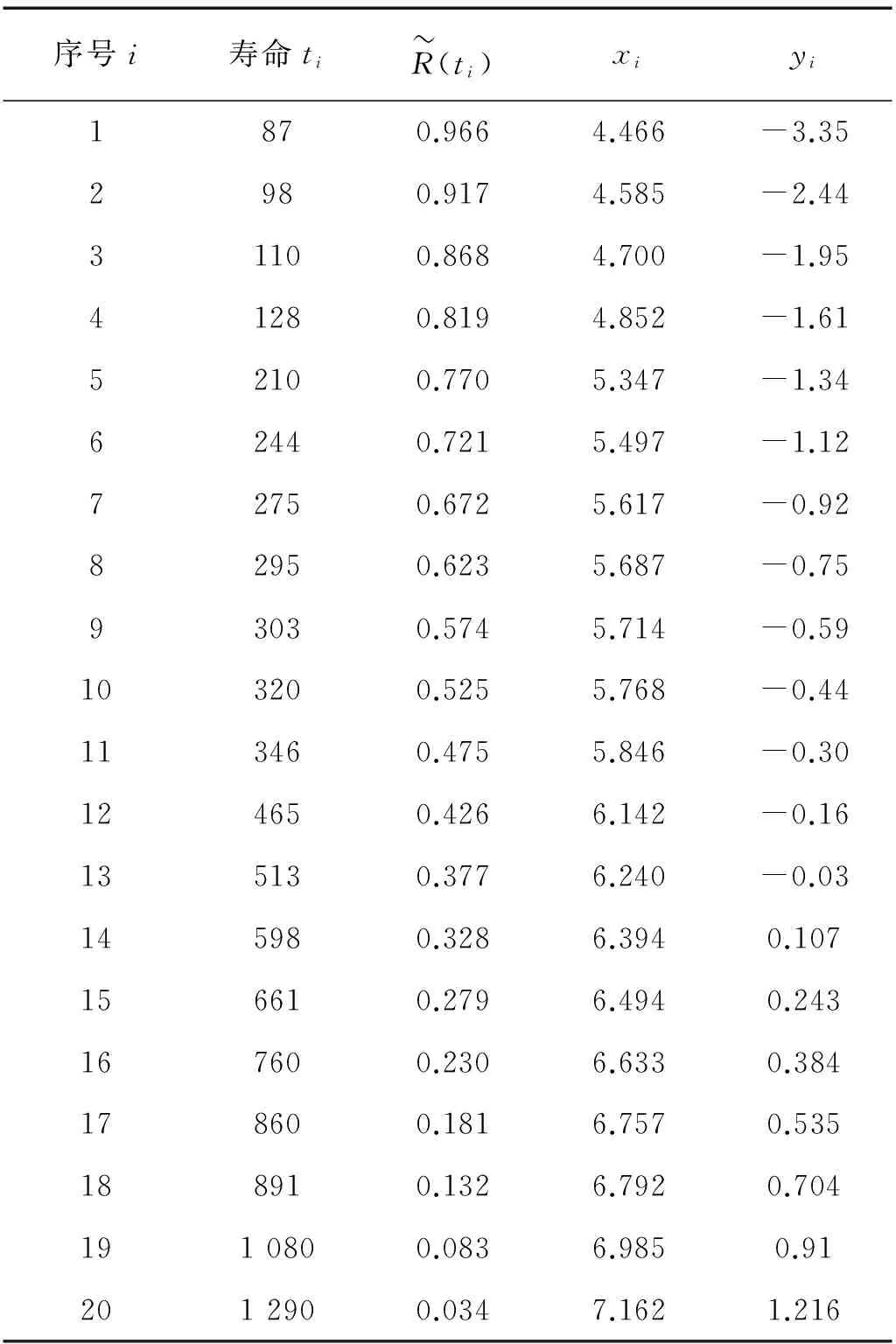
表1 轴子失效数据Tab.1 Rotor failure data

假设汽轮机轴承转子寿命服从三参数威布尔分布，按照图解法的计算步骤在WPP上标记出20组样本的位置，如图3所示。

图3 转子失效数据WPP图Fig.3 The WPP graph of rotor failure data

通过拟合计算，得出两条渐近线方程：

(20)

由此得出威布尔分布三参数的值：β=1.08,η=485.5,γ=80。将此计算结果作为混沌模拟退火粒子群优化算法的初始解，设置初始参数为：c1=c2=2.25，ω=0.35，ε=3.85，δ=0.5。初温T0=160，q=2.3。通过MATLAB程序运算后得出γ,η,β在每一步的运算值如表2所示。在迭代的第38步得出最优值：β=0.998,η=430.15,γ=73.56

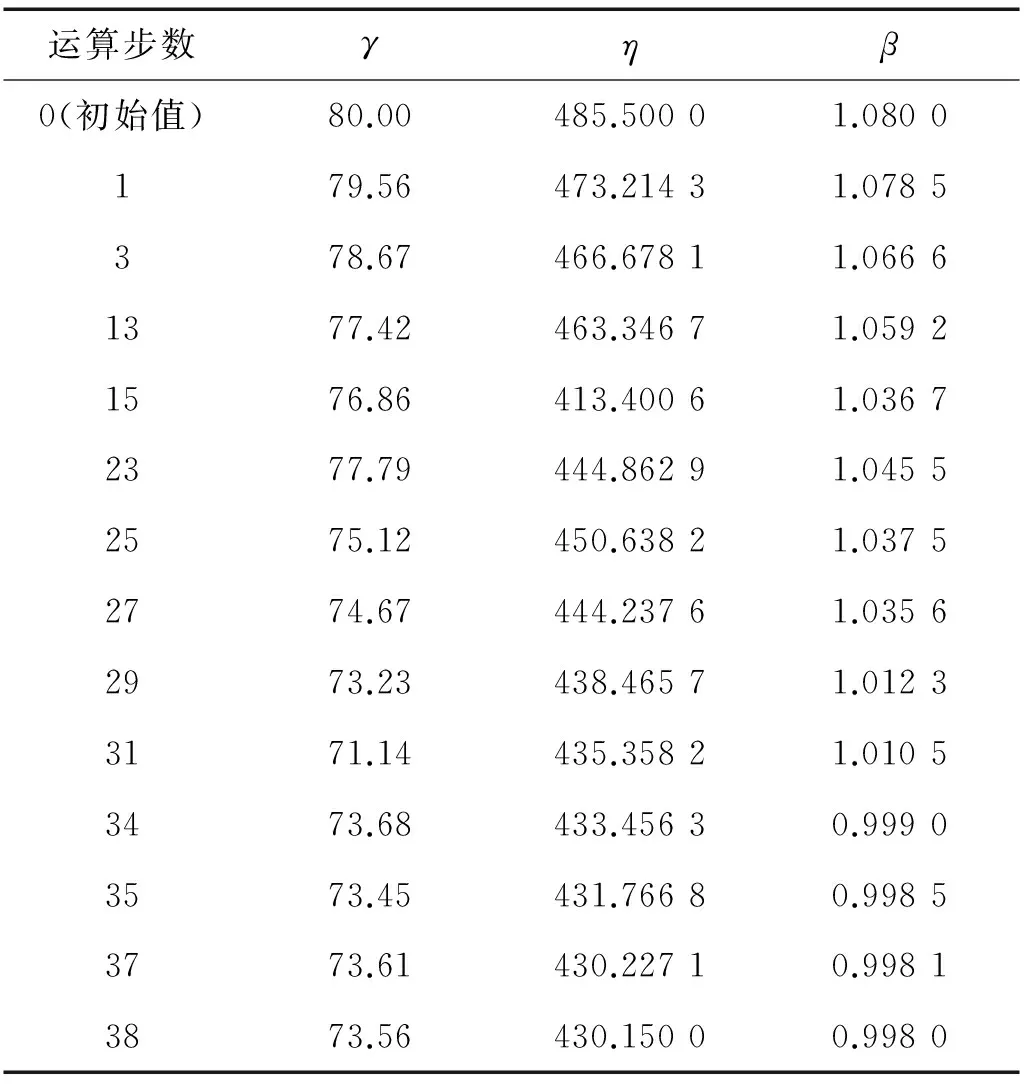
表2 计算值Tab.2 Operation value

为了比较混沌模拟退火PSO算法同其它优化算法的差异和优缺点，在研究过程中也采用了模拟退火PSO算法和遗传算法进行参数优化，图4是三种算法的优化过程对比图。

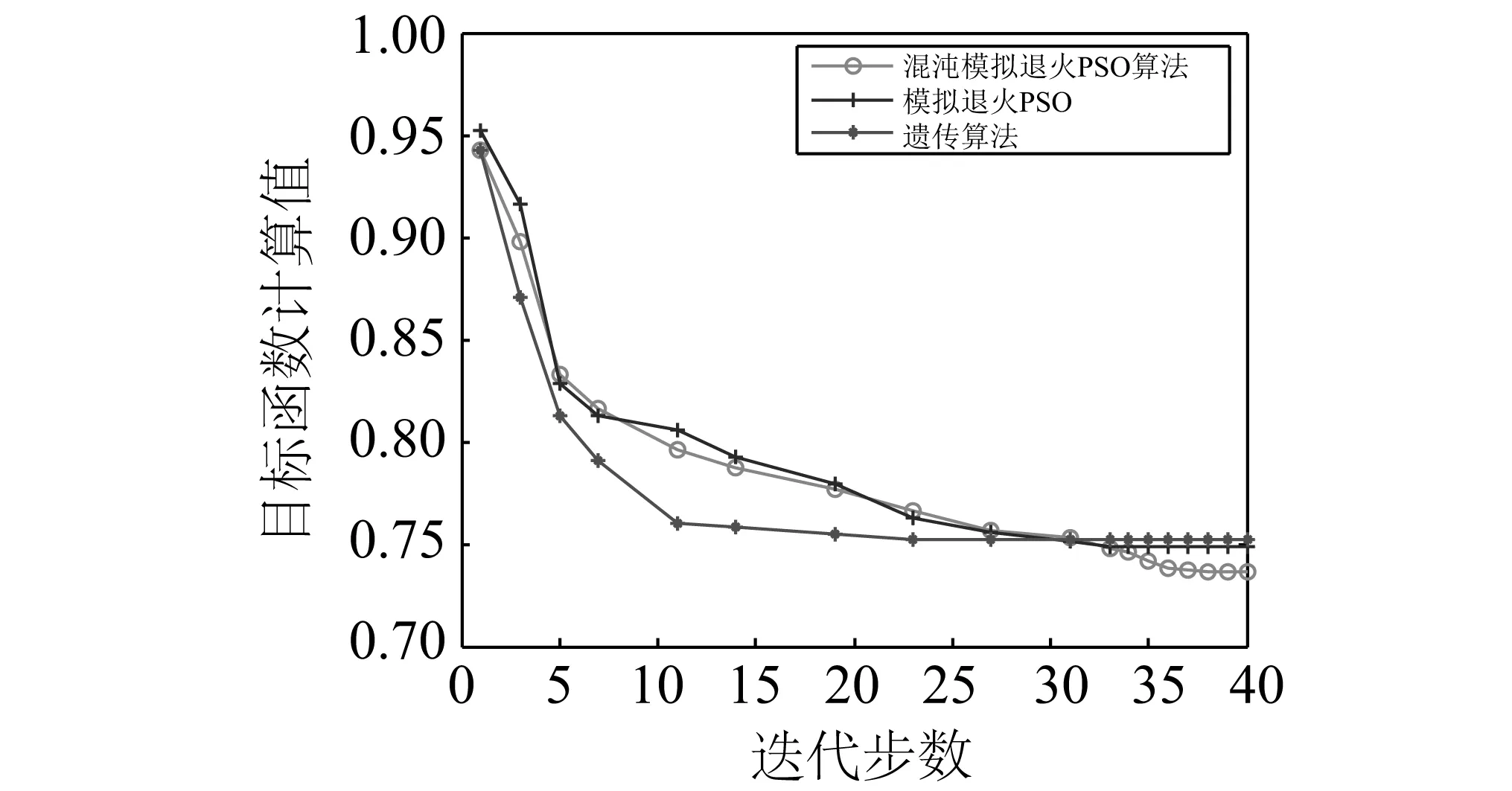
图4 优化过程对比图Fig.4 Contrast figure of optimization process

从图4可知，三种算法均能收敛找到全局最优值。混沌模拟退火PSO算法在第38步找到最佳位置，最优值Δ1(x,t)=0.736 032；模拟退火PSO算法的最佳位置在第35步，Δ2=(x,t)=0.748 29；遗传算法的最佳位置在第33步产生，Δ3(x,t)=0.752 35。收敛速度：遗传算法>模拟退火PSO算法>混沌模拟退火PSO算法，精度：混沌模拟退火PSO算法>模拟退火PSO算法>遗传算法。由于混沌模拟退火PSO算法采用的是用混沌因子来调整粒子群的更新同避免粒子因“早熟”产生聚集的模拟退火方法相结合的策略，因此导致算法在迭代时间上增加了额外的开销，但从图4可知，迭代过程较另外两种方法更加平稳且寻优能力更强。混沌模拟退火PSO算法只比模拟退火PSO算法和遗传算法分别多了3和5步，但精度提高了1.665%和2.217%。

图5是采用三种算法进行优化的最终结果，从图5的对比可知，混沌模拟退火PSO算法的优化最合理，均匀的分布在所有散点的两侧。计算所有散点到各曲线的方差，得出混沌模拟退火粒子群优化算法的方差为0.025 1；模拟退火粒子群优化算法的方差为0.055 9；遗传算法的方差为0.089 7。方差的计算结果也反映出混沌模拟退火粒子群算法优化效果较其它两种方法都好。

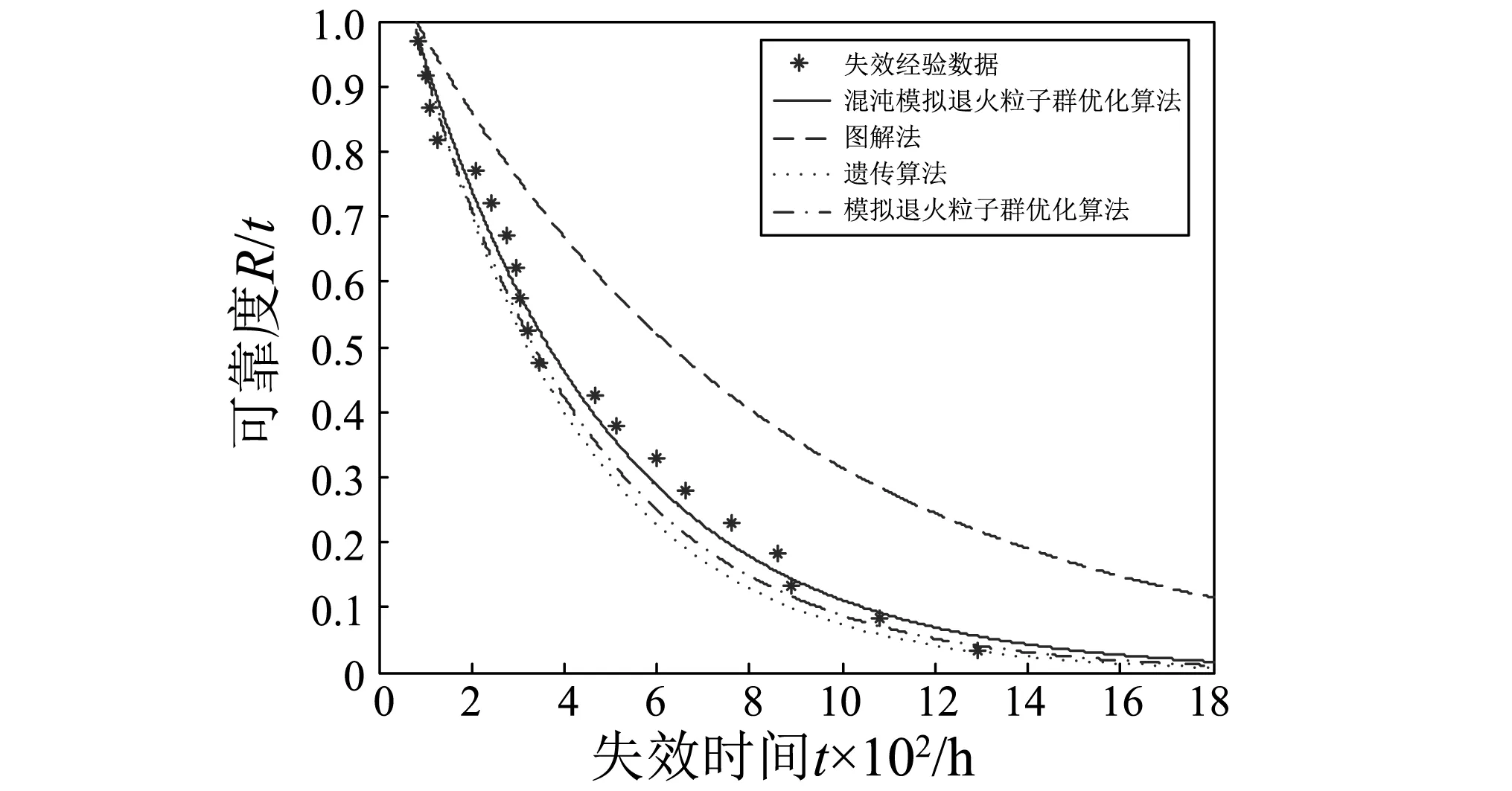
图5 转子可靠度三参数威布尔分布优化曲线Fig.5 Rotor reliability curve of three parameter Weibull distribution

4 结 论

本文将Logistic混沌因子引入到粒子群算法中调整局部加速因子、全局加速因子的更新策略降低了粒子的相对拥挤度，调整惯性权值的更新策略使全局最优值和局部最优值的平衡搜索能力得到加强。采用模拟退火方法保证了算法在引入混沌理论后不至于局部迭代步数过长，开销时间过大。在机械轴承转子寿命威布尔分布三参数优化实验分析中建立了优化方程，将图解法所求得的解作为混沌模拟退火PSO算法的初值。优化求解过程表明算法思想可行，同其他优化方法相比迭代步数稍有增加但搜索过程更加平稳，精度得到了提高。

[1] SHIMIZUA S. P-S-N/P-F-L curve approach using three-parameter Weibull distribution for life and fatigue analysis of structural and rolling contact components [J]. Tribology Transactions, 2005, 48(4): 576-582.

[2] 凌丹.威布尔分布模型及其在机械可靠性中的应用研究 [D]. 成都: 电子科技大学, 2010.

[3] ZHANG L F, XIE M, TANGGA L C. A study of two estimation approaches for parameters of Weibull distribution based on WPP [J]. Reliability Engineering & System Safety,2007, 92(3):360-368.

[4] TOUW A E. Bayesian estimation of mixed Weibull distributions[J]. Reliability Engineering & System Safety, 2009, 94(2): 463-473.

[5] 董胜，韩意，陶山山，等. Weibull分布参数的粒子群算法估计[J]. 中国海洋大学学报, 2012, 42(6): 120-125. DONG Sheng, HAN Yi, TAO Shanshan, et al. Parameters estimation for Weibull distribution with particle swarm optimization[J].Ocean University of China, 2012, 42(6): 120-125.

[6] 杨志忠，刘瑞元. 三参数Weibull分布参数估计求法改[J]. 工程数学学报, 2004, 21(2): 281-284. YANG Zhizhong, LIU Ruiyuan. Improved methods of the parameter estimating of three-parameter Weibull distribution[J]. Journal of Engineering Mathematics, 2004, 21(2): 281-284.

[7] 杨谋存，聂宏. 三参数Weibull分布参数的极大似然估计数值解法[J]. 南京航空航天大学学报，2007, 39(1): 22-24. YANG Moucun, NIE Hong. Advanced algorithm for maximum likelihood estimation of three parameter Weibull distribution[J]. Journal of Nanjing University of Aeronautics & Astronautics，2007, 39(1): 22-24.

[8] 潘晓春. 风速概率分布参数估计的低阶概率权重矩法[J]. 中国电机工程学报, 2012, 32(5): 132-136. PAN Xiaochun. Low-order probability-weighted moments method for wind speed probability distribution parameter estimation[J]. Proceeding of the CSEE, 2012, 32(5): 132-136.

[9] CLERC M. Discrete particle swarm optimization illustrated by the traveling salesman problem [M].Heidelberg：Springer，2004.

[10] 梁洁，蔡琦，初珠立. 基于微粒群优化的贝叶斯网络结构学习方法[J]. 华中科技大学学报(自然科学版), 2012, 40(12): 44-48. LIANG Jie, CAI Qi, CHU Zhuli. Bayesian network structure learning algorithm using particle swarm optimization[J].Huazhong Univ of Sci & Tech(Natural Science Edition), 2012, 40(12): 44-48.

[11] 罗航，王后军，黄建国，等. 基于PSO的三参数威布尔分布参数的联合估计方法[J]. 仪器仪表学报, 2009, 30(8): 1605-1612. LUO Hang, WANG Houjun, HUANG Jianguo, et al. Method of united estimation to the parameter of three-parameter Weibull distribution based on PSO[J]. Chinese Journal of Scientific Instrument, 2009, 30(8): 1605-1612.

[12] 王琼，王磊，任伟建.基于FPSO-SA算法的威布尔分布参数估计研究[J]. 吉林大学学报(信息科学版), 2014, 32(5): 476-483. WANG Qiong, WANG Lei, REN Weijian. Research on estimating parameters of Weibull distribution model based on FPSO-SA[J].Journal of Jilin University(Information Science Edition) , 2014, 32(5): 476-483.

[13] 刘爱军，杨育，李斐. 混沌模拟退火粒子群优化算法研究及应用[J]. 浙江大学学报(工学版), 2013, 47(10): 1722-1730. LIU Aijun, YANG Yu, LI Pei. Chaotic simulated annealing particle swarm optimization algorithm research and its application[J]. Journal of Zhejiang University(Engineering Science) , 2013, 47(10): 1722-1730.

[14] 黄平.粒子群算法改进及其在电力系统的应用[D].广州：华南理工大学, 2012.

[15] 庞峰. 模拟退火算法的原理及算法在优化问题上的应用[D]. 长春：吉林大学，2006.

[16] 郑锐.三参数威布尔分布参数估计及在可靠性分析中的应用[J].振动与冲击,2015,34(5):78-81. ZHENG Rui.Parameter estimation of three-parameter Weibull distribution and its application in reliability analysis[J].Journal of Vibration and Shock,2015,34(5):78-81.

[17] NELSON E W. Applied life data analysis [M].New York:John Wiely & Sons Inc.，1982.

A chaotic simulated PSO algorithm application for Weibull distribution parameter estimation

XU Wei， CHENG Gang， HUANG Lin, WEI Xiulei, WENG Lei

(Power and Enginering Academy, Naval University of Engineering, Wuhan 430033, China)

Aiming at the deficiency in the precise solution for the three-parameter Weibull distribution model, the parameter estimation based on a chaotic simulated annealing particle swarm optimization algorithm was proposed, and the Logistic chaos factor was introduced to adjust the update strategy of the particle swarm optimization algorithm to fully release its ergodic search ability. The simulated annealing method was used to accept the new state with a certain probability according to the acceptance criteria of Tsallis, so that the algorithm could avoid premature convergence and realize the global optimal search. At the same time, in order to reduce the time of iterative calculations, the initial solution obtained by the graphic method was used to provide the search scope. The method was applied to the reliable Weibull distribution parameter estimation of a bearing rotor. Experimental results show that the method is feasible and effective and has better optimization performance compared with a genetic algorithm and a simulated particle swarm optimization algorithm.

chaos; simulated annealing; particle swarm optimization(PSO); Weibull distribution; parameter estimation

国家自然科学基金资助项目(51579242)；湖北省自然科学基金项目(2013CFB)

2016-04-05 修改稿收到日期： 2016-10-24

许伟 男，博士，1987年生

程刚 男，教授，1965年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.12.022