基于正交试验、组合赋权-灰色关联的机床横梁优化设计

邱自学，鞠家全，任 东，崔德友，刘传进

(1. 南通大学 机械工程学院，江苏 南通 226019； 2. 南通国盛机电集团有限公司，江苏 南通 226003)

基于正交试验、组合赋权-灰色关联的机床横梁优化设计

邱自学1，鞠家全1，任 东2，崔德友2，刘传进2

(1. 南通大学 机械工程学院，江苏 南通 226019； 2. 南通国盛机电集团有限公司，江苏 南通 226003)

机床横梁是机床的重要部件，横梁的刚性对机床的加工精度影响很大，为此，需要对横梁结构进行优化设计以获得良好的静、动态特性。设计了6种横梁筋板结构，初步筛选出4种筋板结构的横梁，并以横梁筋板结构、筋板厚度、上导轨支撑筋板倾斜角度为试验因素，以横梁质量、最大耦合变形、最大耦合应力、一阶固有频率为评价指标设计了三因素四水平的正交试验；采用灰色关联法和组合赋权法处理有限元分析数据，获得优化设计的最优参数组合。结果表明，横梁“井”型筋板结构，筋板厚度25 mm，上导轨支撑筋板倾斜45°设计为最优方案，与原设计方案相比质量减轻了466 kg，横梁总形变减少了7.36%，一阶固有频率提高了2.91%。拓展了正交试验、组合赋权-灰色关联法的应用范围，为其它机床零部件的设计提供了有益的方法参考。

机床横梁；优化设计；正交试验；组合赋权；灰色关联；有限元法

机床行业作为装备制造业的重要领域，也正在随着中国经济一起步入了一个新的历史发展阶段[1]；在这一新常态下，给国内的制造业，特别是机床行业带来了不小的挑战，但是，对于有一定规模的企业来说这既是挑战，更是机遇。企业只有通过技术创新，产品升级，提高产品质量才能立于不败之地。横梁作为机床的重要部件，其结构设计是否合理，直接影响着机床刚度及加工精度[2-4]，近年来，横梁已经成为众多学者的研究对象。

谢黎明等对机床横梁内部的筋板结构，筋板的数量进行了优化设计，提出将横梁内部筋板改为X型，数量由3块变为5块，厚度由10 mm增加到15 mm，横梁内部增加纵向筋板等措施，通过有限元分析法分析了优化前后横梁的静、动态性能，证明了优化设计的可行性；唐振宇等设计了4种筋板结构的横梁，通过有限元分析证明了O型筋板结构的横梁为最优方案；候红玲等对截面不同的几种横梁结构进行了静、动态特性分析，通过模态分析挑选出矩形截面横梁为最优结构方案；王艳青等[5]根据加工中心的加工要求，设计出横梁筋板的类桁架结构形式，通过对4种横梁静力学分析，证明优化后的横梁具有较高的结构刚性；刘兴卓等[6]对铣床横梁直线导轨仿形装置进行仿形加工设计，降低了机床横梁仿形加工的难度，提高了机床加工的精度。

本文中设计了6种筋板结构的横梁，挑选出4种结构横梁进行了三因素四水平的正交试验，以横梁筋板结构、筋板厚度、上导轨支撑筋板倾斜角度作为试验因素，以横梁质量、最大耦合变形、最大耦合应力、一阶固有频率作为评估指标，采用组合赋权和灰色关联法处理数据，挑选出最佳的参数组合，得到最佳的方案。

1 横梁结构的设计

1.1 原横梁有限元分析

如图1所示，横梁部件包括横梁、滑板、滑枕等零部件组成，横梁上下导轨上承受着滑板组件(包括滑板，滑枕，油缸座，主轴箱等零部件)的重量，在重载荷作用下横梁往往会发生弯曲变形，从而影响机床的加工精度。

图1 GMM6032龙门加工中心Fig.1 GMM6032 gantry machining center

为简化有限元模型，在进行分析时仅将横梁模型导入有限元分析软件，并将其他零部件对横梁的作用效果等效到横梁对应的作用面上，此外去除了不必要的细小零件和孔，以提高分析的速度[7-8]。如表1所示，为原横梁有限元分析结果。如图2所示，为优化设计的流程，包括原横梁分析、确定试验因素与评价指标、正交试验设计、组合赋权-灰色关联法数据处理等步骤。

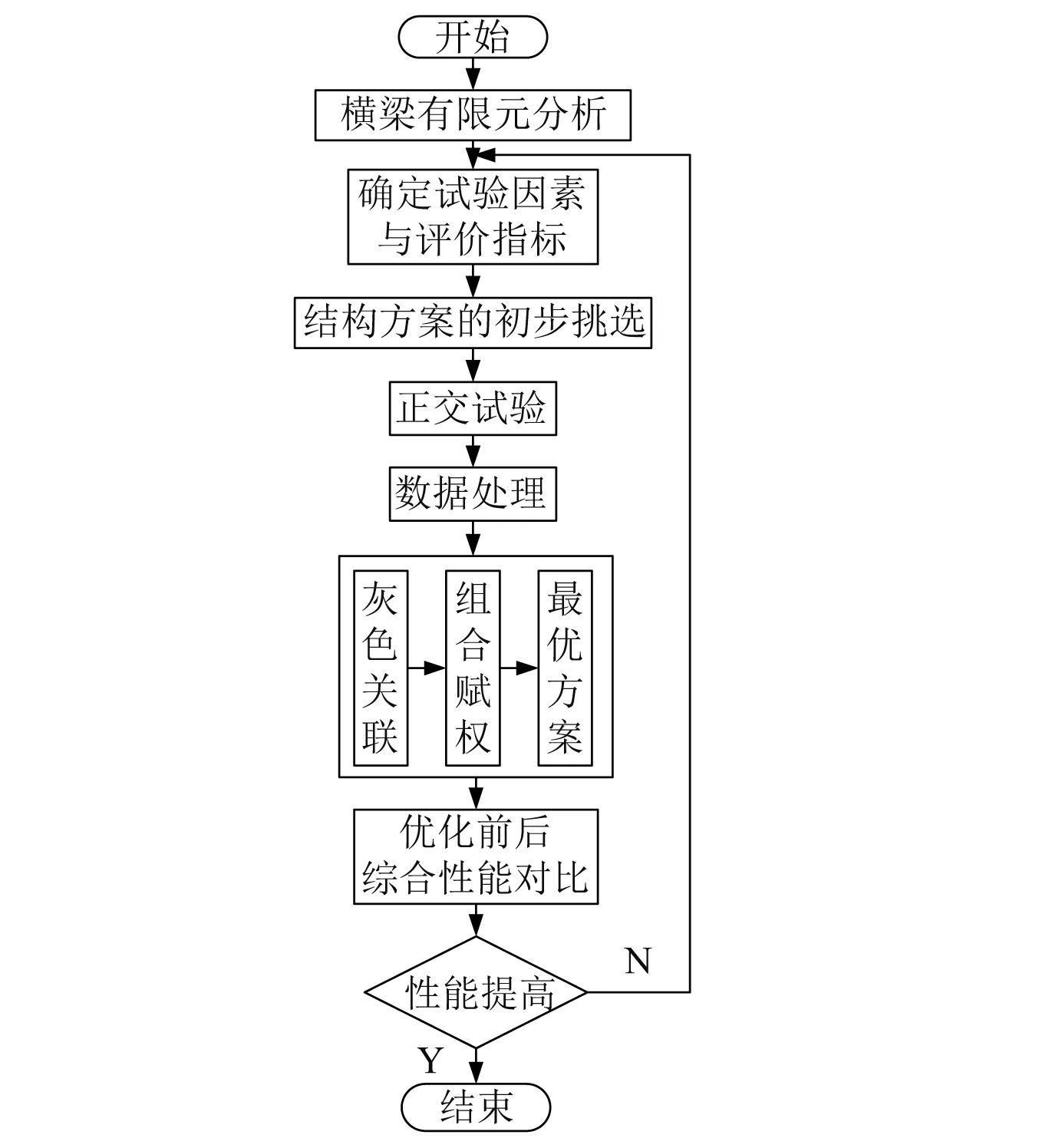
图2 优化设计流程Fig.2 Process of optimization design表1 原横梁静、动态分析Tab.1 Static and dynamic characteristics of the original crossbeam

筋板结构筋板厚度d/mm质量m/kg最大耦合变形δ/μm最大耦合应力σ/MPa一阶固有频率f/Hz米301358536.1094.46138.68

1.2 确定试验因素与评价指标

横梁内部筋板结构和筋板的厚度对横梁的各项性能有着重要的影响，特别是对横梁的质量和最大耦合变形影响最大，因此将筋板结构，筋板厚度作为横梁优化设计的因素。如图3所示，横梁上导轨下侧的支撑筋板倾斜角度θ的不同对横梁的性能有着重要的影响，因此将上导轨支撑筋板倾斜角度作为试验因素，其中原横梁支撑筋板的倾斜角度θ=90°(水平)。

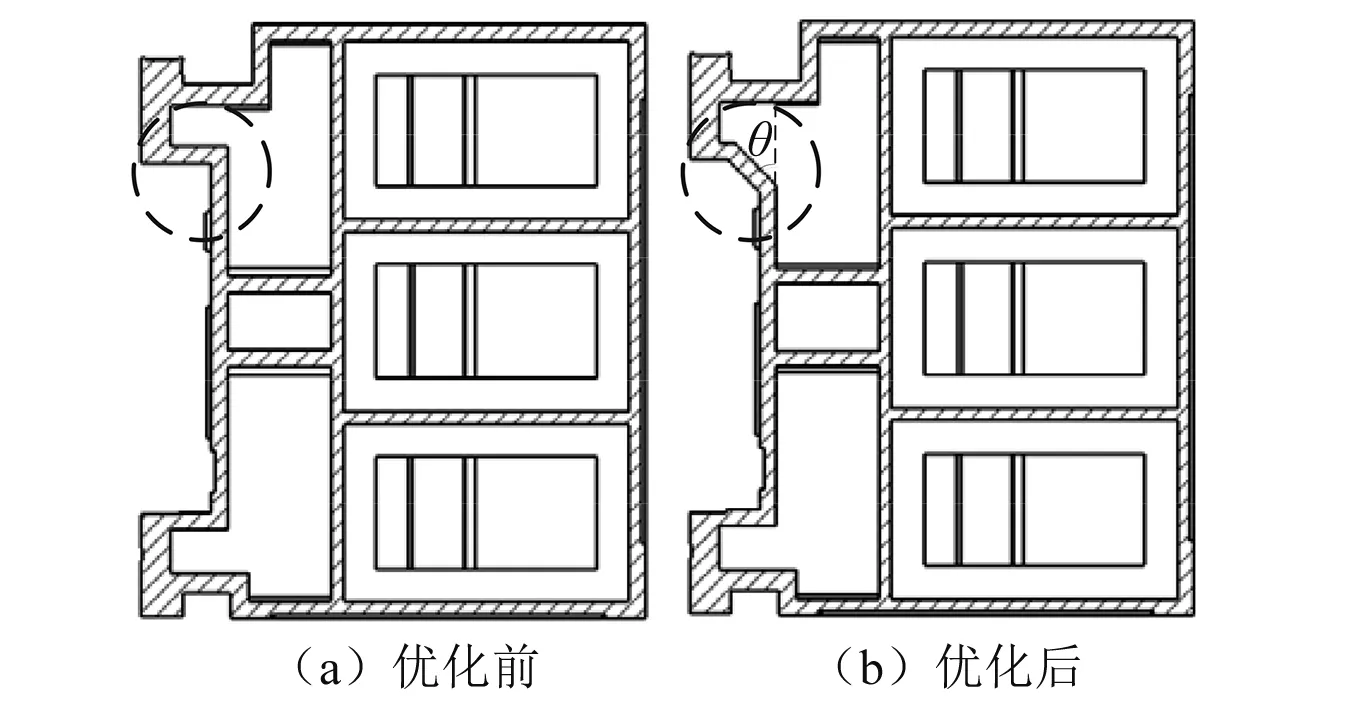
图3 上导轨支撑筋板优化设计Fig.3 Optimization design of support rib on rail

如图4所示，除了原横梁，另外设计了5种筋板结构的横梁。

图4 6种筋板结构Fig.4 Six kinds of rib structure

取筋板厚度30 mm，倾斜角度90°(水平)为不变量，以筋板结构为单一变量，对6种筋板结构的横梁进行有限元分析，分别分析了横梁在受到滑板组件和横梁自重共同作用下的横梁耦合变形(总形变)，以及横梁在仅受自重作用下引起的形变，分析结果，如表2所示。表2中以横梁质量，横梁变形量作为评价指标，其中因横梁自重引起的变形量平均占总形变量的44.9%，说明横梁自重对横梁的弯曲变形影响较大，因此在后续的优化设计中应该将横梁质量作为评价优化设计优劣的重要指标。为减少后续试验的次数，针对表2中6种横梁进行初步筛选，其中M型横梁的最大耦合变形量最大，且远大于原横梁最大耦合变形量36.109 μm；“十字+菱”型横梁的质量最大，且远大于原横梁的质量13 585 kg；因此，将这两种筋板结构的横梁剔除下一步的优化设计。

为提高优化设计中横梁各因素参数选取的准确性与可靠性，文中除了将质量和最大耦合变形作为评价指标外，还将横梁最大耦合应力，一阶固有频率作为评价指标。

表2 六种筋板结构横梁有限元分析Tab.2 Finite element analysis of six kindsof rib structure crossbeam

2 正交试验设计

正交试验设计要考虑如何安排多因素多水平的试验才能合理有效的获得所要的分析数据，并用相应的方法分析这些数据，以确定哪些因素是主要的，各因素用什么水平搭配起来对试验指标才是最佳的[9]。如“1.2”所述，将横梁筋板结构，筋板厚度，上导轨支撑筋板倾斜角度作为正交试验的因素，设计了如表3所示的三因素四水平的正交试验；以横梁质量、最大耦合变形、最大耦合应力，一阶固有频率作为横梁优化设计评价指标，正交试验结果，如表4所示。

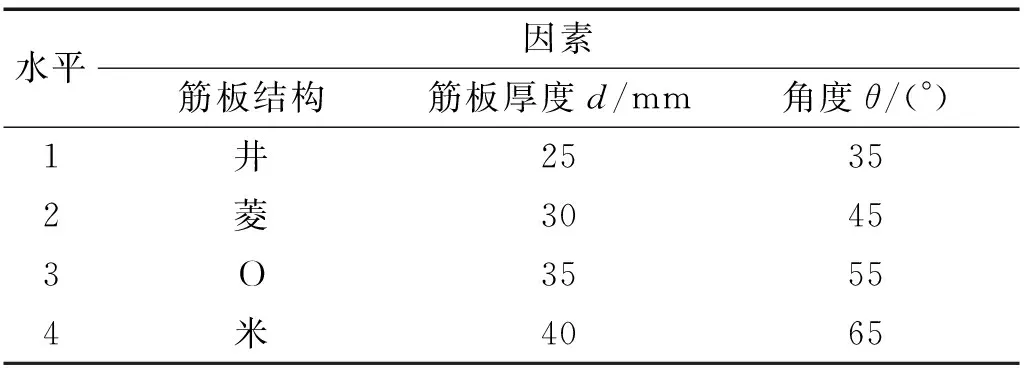
表3 正交试验因素与水平Tab.3 Factors and levels of orthogonal experimental design

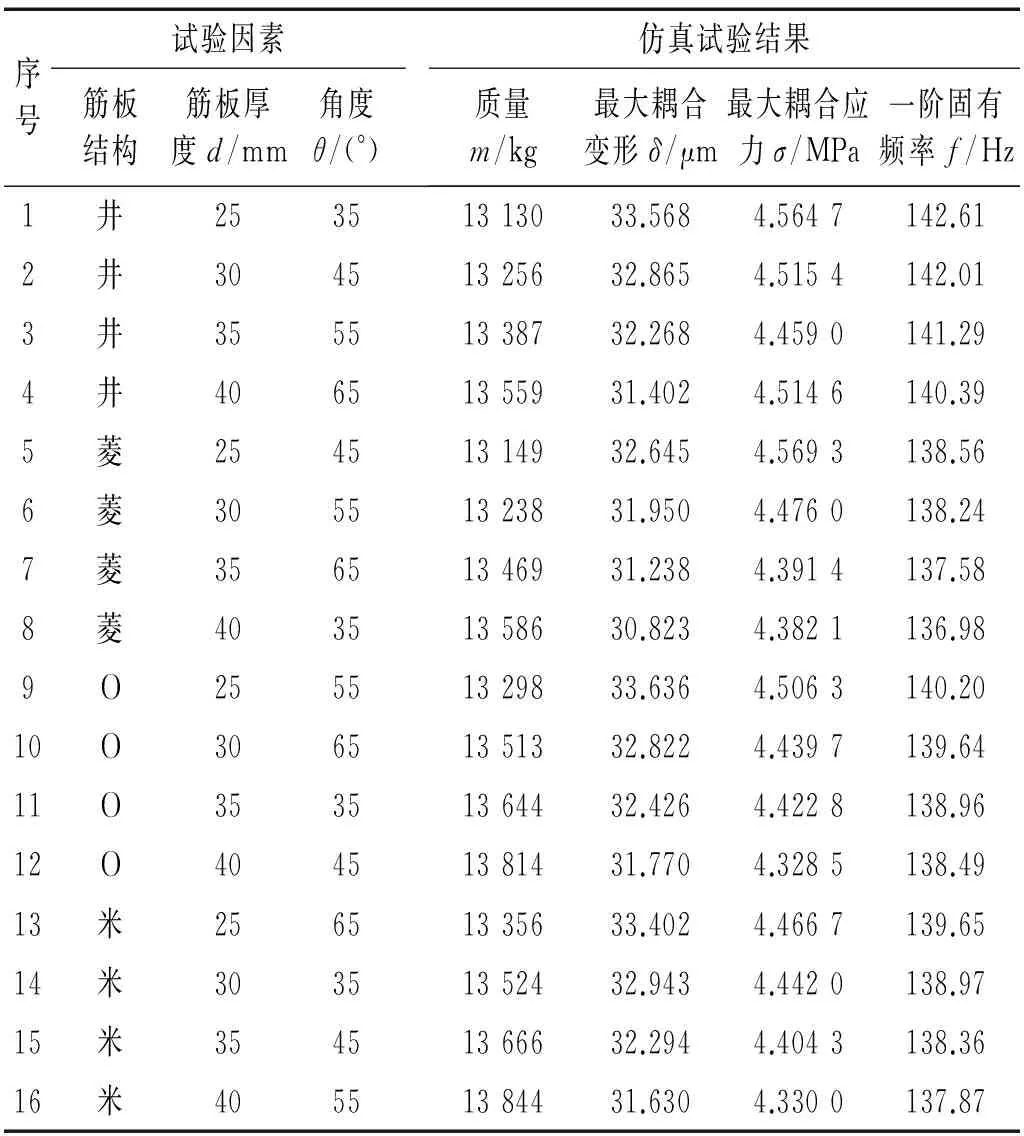
表4 横梁仿真试验结果Tab.4 Simulation results of crossbeam

3 数据处理

3.1 灰色关联法

灰色关联度分析是灰色系统的基本内容，其基本思想是：从原始数据矩阵中找出最佳决策方案，并根据线性比例变换法对评判矩阵进行标准化，之后根据权重系数计算判断矩阵，获得各个方案的投影值，以此作为评价方案优劣的依据[10-14]。

1) 按照灰色关联分析法，假设评价系统中有m个评价指标，n个试验方案，则评价指标矩阵A为：

(1)

根据式(1)将横梁的4个评价指标各仿真数据化为矩阵A。

(2)

2) 对指标矩阵归一化

在系统的各评价指标中，有的是越大越优的指标，有的是越小越优的指标，针对这一现象，对相应的数据作区分处理：

对越大越优的指标：

(3)

对越小越优的指标：

(4)

其中i=1,2,…,n；j=1,2,…,m。

根据式(3)、式(4)处理后，矩阵A变为：

(5)

将各指标中的最大值作为参考方案，参考方案矩阵为：K=[k1k2…km]，其中kj=max(r1j,r2j,…,rnj)，j=1,2,…,m。

3) 关联系数矩阵计算

(6)

式中：分辨系数ρ∈[0,1]，本文中取ρ=0.5，经过式(6)处理后得到关联系数矩阵ζ。

(7)

3.2 组合赋权方法

权重赋值的方法一般有两种：主观赋权法和客观赋权法。主观赋权法的权重由专家依经验主观判断得到，决策结果具有一定的主观随意性，典型的方法有层次分析法(Analytic Hierarchy Process, AHP)、环比评分法、专家打分法(Delphi法)等；客观赋权法的权重是依据原始数据的关系确定的，主要方法有均方差法，熵值法、离差法等[15-16]。文中为了使最终的决策结果更加真实、可靠，从而实现横梁的优化设计，结合了AHP和熵值法确定评估指标的组合权重。

1) 熵值法

对指标矩阵A进行归一化处理：

(8)

各个指标的信息熵：

(9)

熵值法权重：

(10)

2) 组合权重

采用文献[11]中的9级比例标尺，成对比较法确定层次分析法权重(主观权重)ω″j后，对主观权重和客观权重进行组合，组合方法按照文献[12]中组合权重计算方法进行处理，具体公式为：

(11)

3) 理想方案的关联度计算

γ=ζω

(12)

其中ω为ωj(j=1,2,3,…,m)组成的组合权重系数矩阵，γ为目标函数灰色关联度矩阵。

3.3 最优参数组合的确定

横梁各评价指标中一阶固有频率是越大越优的指标，而质量、最大耦合应力、最大耦合变形是越小越优的指标，由式(1)～式(5)得横梁优化设计数据的特征矩阵R：

由式(6)～式(7)计算得灰色关联系数矩阵ζ：

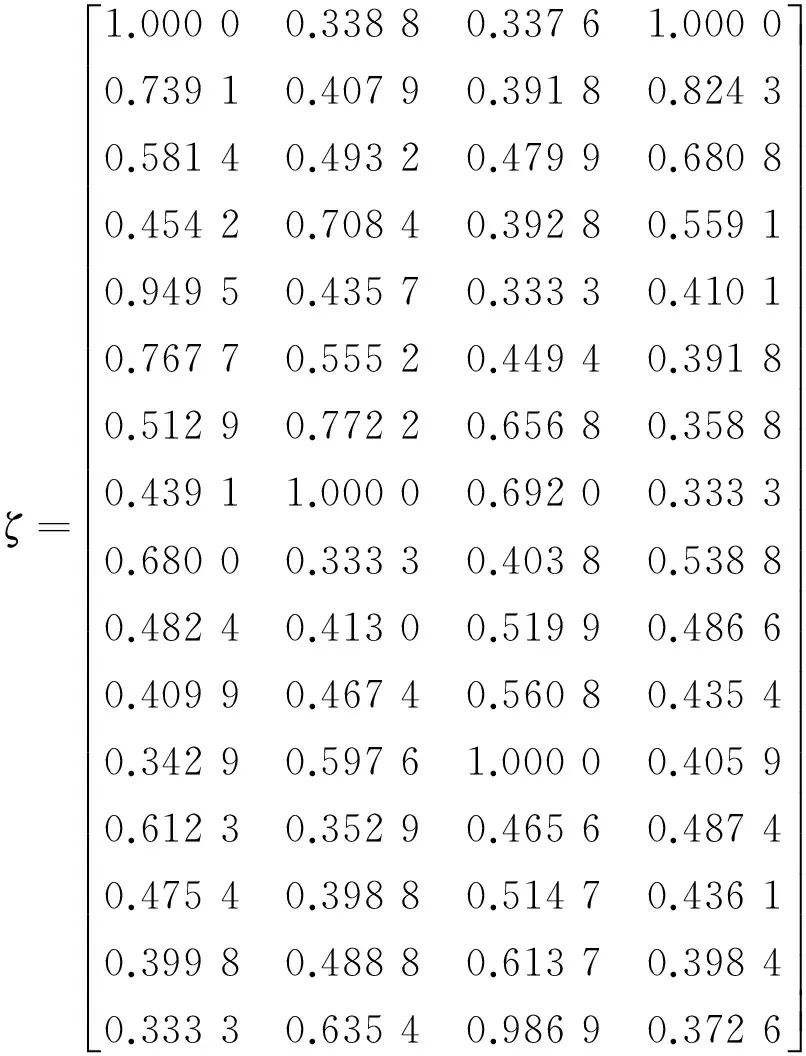
根据式(8)～式(10)进行数据处理，计算得主、客观权重结果分别如下：

客观权重：

主观权重：

ω″j=[0.554 9 0.251 6 0.096 7 0.096 7]

依式(11)计算组合权重为：

ωj=[0.638 6 0.138 8 0.111 3 0.111 3]

由式(12)计算的目标函数的灰色关联度，如表5所示。

表5 目标函数关联度Tab.5 Correlation of objective function

其中各水平的平均关联度，如表6所示。由表6可知，最佳组合方案是筋板结构“井”型，筋板厚d=25 mm，角度θ=45°。

表6 各水平平均关联度Tab.6 Average correlation degree of each level

4 横梁优化设计结果分析

4.1 优选方案的确定

由“3”数据分析得到横梁优化设计参数的最佳组合为“井-25 mm-45°”。但是在正交试验表中并没有这一组数据的组合，说明采用正交试验方法可以在减少试验次数的前提下推断出可能更好的试验参数组合。为了确定该组合就是最佳参数组合，需要对该方案进行仿真试验分析，分析结果，如表7所示。

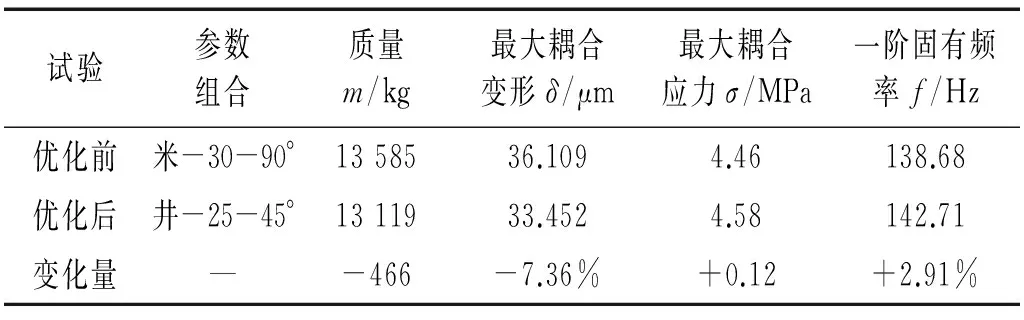
表7 优化前后横梁有限元分析Tab.7 Finite element analysis of crossbeam beforeand after optimization

如表7所示，横梁在最大耦合应力仅增加0.12 MPa的情况下，质量减轻了466 kg，最大耦合变形减少了7.36%，一阶固有频率提高了2.91%；虽然优化后横梁最大耦合应力有所增加，但是其值远远小于材料HT300的许用应力，因此机床横梁的静、动态性能得到明显改善。

4.2 多种分析方法的结果比较

为进一步说明文中采用方法的合理与先进性，另外采用了三种方法对横梁的优化数据进行了处理，方法如表8所示，其中限于篇幅，各方法的具体实施步骤不做具体说明。

各方法的优选方案结果，如表9所示。综合比较四种优选方案结果：

(1) 相对最优方案为“井-25 mm-55°”；

(2) 方法三优选的“菱-25 mm-55°”方案，其质量在四种方案中最重，一阶固有频率在四种方案中最小，与最优方案差距较大；

(3) 采用方法四优选的方案与方法一和二不同之处在于倾斜角度的选择，对比优选结果各评价要素的值，其中最大耦合变形量、最大耦合应力、一阶固有频率两方案数值很接近，基本可忽略之间的误差值，质量相差7 kg，误差也很小。

表8 四种数据处理方法Tab.8 Four kinds of data processing methods

综合分析可知，方法四与方法一和方法二优选结果最接近，但是方法一在最终的结论分析中容易出现多个优选方案，特别是在多因素多水平的正交试验设计中，多数情况下需要进行数据的二次分析处理，甚至需要二次正交试验设计，降低了效率，增加了数据处理的繁琐程度。方法二在数据处理过程中，针对数据处理只采用了主观赋权法，其权重的选择具有一定的随意性，在复杂类问题的处理过程中势必会降低优选结果的准确性。方法三在数据的处理过程中，主要依赖于数据本身作出主观的判断，方案的选择和判断上也存在着一定的主观随意性，特别是针对影响因素多，数据量大的工程类问题时，步骤和试验多，基本不会采用方法三。方法四采用正交试验，组合赋权和灰色关联方法，不仅一次性考虑了影响的主要因素，而且综合考虑了客观因素和主观因素，使优选结果更加真实、可靠。因此，本文中采用正交试验、组合赋权-灰色关联方法选择横梁最佳参数组合是合理可靠的。

表9 多种方法结果对比Tab.9 Results comparison between several methods

5 结 论

(1) 对横梁仅在自重，滑板组件重力和自重共同作用的情况下进行了分析，因横梁自重引起的变形占总形变量的44.9%，说明因横梁自重引起的横梁弯曲变形占有较大的比例，因此在对横梁等大型零部件的设计与优化中，应该将零件重量作为评价设计优劣的重要指标。

(2) 针对受力变形最大的上导轨部位，将其下端的支撑筋板由原来的水平设计变为倾斜45°的设计，对减少横梁上导轨面变形和减轻横梁质量起到了重要的作用。运用正交试验设计方法实现对横梁的多目标优化设计，并且采用组合赋权-灰色关联方法分析试验数据，综合考虑主观和客观因素，实现以较少的试验次数，获得最佳试验参数组合。此外，通过对比多种优化方法，说明了正交试验，组合赋权-灰色关联法的合理可靠性，及较强的工程实用性。

(3) 优化设计后的横梁质量减轻了466 kg，最大耦合变形减少了7.36%，一阶固有频率提高了2.91%，横梁综合性能得到了有效提高，优化设计效果明显。

(4) 本文中以横梁内部筋板结构、筋板厚度和上导轨支撑筋板结构作为试验因素，以横梁质量、最大耦合变形、最大耦合应力和一阶固有频率作为评估指标，运用组合赋权法和灰色关联法处理分析数据从而实现横梁最优参数组合的选取。在以后的研究中，如果将横梁外形尺寸、横梁箱体结构的壁厚等，也作为试验的因素，并且结合灵敏度分析方法，将进一步提高横梁各参数选取的精确性，提高横梁的综合性能。

[1] 梁玉. 新常态、新发展——记2015机床制造业CEO国际论坛[J]. 制造技术与机床，2015(6): 21-23.LIANGYu.Newnormal,newdevelopment—ReportoninternationalCEOforumofmachinetoolmanufacturingindustry[J].ManufacturingTechnology&MachineTool, 2015(6): 21-23.

[2] 谢黎明，李大明，沈浩，等. 基于有限元分析的现场铣床横梁结构优化[J]. 组合机床与自动化加工技术，2008(9): 37-39. XIE Liming, LI Daming, SHEN Hao, et al. Optimization design of scene milling machine based on finite element analysis[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2008(9): 37-39.

[3] 唐振宇，李锻能. 大型龙门式加工中心横梁筋板设计与分析[J]. 机床与液压，2011,39(22):40-42. TANG Zhenyu, LI Duanneng. Design and analysis of beam stiffened plates of large gantry machine center[J]. Machine Tool & Hydraulics, 2011,39(22):40-42.

[4] 候红玲，邱志惠，赵永强. 高速切削机床横梁的静态与动态分析[J]. 机械设计与制造，2006(5): 38-39. HOU Hongling, QIU Zhihui, ZHAO Yongqiang. Static & dynamic analysis for beam of high-speed cutting machine tool[J]. Machinery Design & Manufacture, 2006(5):38-39.

[5] 王艳青，仲高艳，常永标，等. 大型五轴联动加工中心横梁结构的设计[J]. 机床与液压，2012, 40(13): 114-117. WANG Yanqing, ZHONG Gaoyan, CHANG Yongbiao, et al. Design of beam structures for large five-axis machining center[J]. Machine Tool & Hydraulics, 2012, 40(13): 114-117.

[6] 刘兴卓，喻鹏，苏文涛. 立式车铣中心横梁导轨的仿形设计和制造方法[J]. 机床与液压，2013, 41(14): 14-17. LIU Xingzhuo, YU Peng, SU Wentao. Copying design and manufacturing approach of crossrail guideway vertical turning and milling center[J]. Machine Tool & Hydraulics, 2013, 41(14): 14-17.

[7] 王宇清，曹忠亮. 大型铣床横梁模态分析及装配改进方法研究[J]. 制造技术与机床，2014(9): 137-139. WANG Yuqing, CAO Zhongliang. Research on large milling beam modal analysis and improved assembling[J]. Manufacturing Technology & Machine Tool, 2014(9): 137-139.

[8] 张森，杨玉萍，邱自学，等. 基于灵敏度分析的龙门加工中心横梁轻量化设计[J]. 机械设计，2015, 32(4): 110-115. ZHANG Sen, YANG Yuping, QIU Zixue, et al. Lightweight design for crossbeam of gantry machining-center based on sensitivity analysis[J]. Journal of Machine Design, 2015, 32(4):110-115.

[9] 王岩，隋思涟. 试验设计与MATLAB数据分析[M]. 北京：清华大学出版社，2012.

[10] 孙鹏霄. 灰色关联方法的分析与应用[J]. 数学的实践与认识，2014, 44(1): 97-101. SUN Pengxiao. Analysis and application of gray correlation method[J]. Mathematics in Practice and Theory, 2014, 44(1): 97-101.

[11] 张炳江. 层次分析法及其应用案例[M]. 北京：电子工业出版社，2014.

[12] 唐兴中，蓝明新，经建芳，等. 基于组合赋权——灰色关联投影法的润滑配方优选[J]. 润滑与密封，2014, 39(6): 108-111. TANG Xingzhong, LAN Mingxin, JING Jianfang, et al. Optimization of lubricant formulation based on combination weight-grey relation projection method[J]. Lubrication Engineering, 2014, 39(6): 108-111.

[13] 刘思峰，蔡华，杨英杰，等. 灰色关联分析模型研究进展[J]. 系统工程理论与实践，2013, 33(8): 2041-2044. LIU Sifeng, CAI Hua, YANG Yingjie, et al. Advance in grey incidence analysis modeling[J]. Systems Engineering—Theory & Practice, 2013, 33(8): 2041-2044.

[14] 刘世豪，叶文华，陈蔚芳，等. 基于正交试验和灰色关联的机床主轴箱优化设计[J]. 振动与冲击，2011, 30(7): 127-132. LIU Shihao, YE Wenhua, CHEN Weifang, et al. Optimizaton design for headstock of machine tool based on orthogonal experimental method and grey relational analysis[J]. Journal of Vibration and Shock, 2011, 30(7): 127-132.

[15] 宋明顺，黄佳，张士朋，等. 多指标正交试验设计去量纲准则及方法研究[J]. 工业工程与管理，2014, 19(1): 41-46. SONG Mingshun, HUANG Jia, ZHANG Shipeng, et al. The research on the dimensionless criterion and methods about the design of multi-index orthogonal experiment[J]. Industrial Engineering and Management, 2014, 19(1): 41-46.

[16] 孙晓东，焦玥，胡劲松. 基于组合权重的灰色关联理想解法及应用[J]. 工业工程与管理，2006(1): 62-66. SUN Xiaodong, JIAO Yue, HU Jinsong. Grey correlation based on combinational weight and its application[J]. Industrial Engineering and Management, 2006(1): 62-66.

[17] 苏劲，袁智，侍玉苗，等. 水力旋流器细粒分离效率优化与数值模拟[J]. 机械工程学报，2011, 47(20): 183-188. SU Jing, YUAN Zhi, SHI Yumiao, et al. Separation efficiency optimization of liquid-solid hydroclone and numerical simulation[J]. Journal of Mechanical Engineering, 2011, 47(20): 183-188.

Optimization design for the crossbeam of a machining tool based onthe orthogonal experimental method and combination weight-grey relational analysis

QIU Zixue1, JU Jiaquan1, REN Dong2, CUI Deyou2, LIU Chuanjin2

(1. School of Mechanical Engineering, Nantong University, Nantong 226019, China;2. Nantong Guosheng Electromechanical Group Company Ltd., Nantong 226003, China)

The crossbeam is an important part of a machining tool. The stiffness of the crossbeam has great impact on machining accuracy; therefore, optimization design of the crossbeam is necessary to obtain good static and dynamic characteristics. Six kinds of rib structure were designed and were preliminary screened out four kinds of them. The orthogonal experimental method was carried out with three levels and four factors, which took the crossbeam’s rib structure, the rib thickness, the angle of supporting ribs on guide-way as design variables, and took the crossbeam’s quality, the maximum coupling deformation, the maximum coupling stress, the first-order frequency as objective functions. The Grey correlation method and the combination weighting method were used to process the data of finite element analysis to obtain optimal parameter combination. The results show that the crossbeam with “井” type rib structure, rib thickness of 25 mm, the supporting ribs on guide-way tilted 45° is the optimal solution. Compared with the original design, the beam deformation reduced by 7.36% and the first-order frequency increased by 2.91%, while the mass reduced by 466 kg.

crossbeam of machine tool; optimization design; orthogonal experimental method; combination weight; grey relational analysis; finite element method

南通市重大科技创新专项(XA2014011)；江苏省产学研前瞻性联合研究项目(BY2015047-11)

2016-03-06 修改稿收到日期： 2016-04-26

邱自学 男，博士，教授，博士生导师，1963年生

TH122; TG502

A

10.13465/j.cnki.jvs.2017.12.018