斜拉索干索驰振机理的数值模拟与试验研究

李寿英， 曾庆宇， 温晓光， 陈政清

(湖南大学 风工程与桥梁工程湖南省重点实验室， 长沙 410082)

斜拉索干索驰振机理的数值模拟与试验研究

李寿英， 曾庆宇， 温晓光， 陈政清

(湖南大学 风工程与桥梁工程湖南省重点实验室， 长沙 410082)

采用数值模拟和风洞试验方法，对斜拉索干索驰振机理进行研究。基于FLUENT商业软件平台，研究斜索和直索的风压系数、平均气动力系数、脉动气动力系数的轴向相关性等；进行粒子图像测速(PIV)风洞试验，对斜索尾流进行可视化显示，研究斜拉索背后的轴向流特性。研究结果表明：斜索的平均升力系数在特定的倾角和风攻角下会发生突降，其驰振力系数为较大的负值(-4.74)，可能会发生驰振；斜索各截面气动力的轴向相关系数比直索要小，甚至会出现负的相关系数；在平均气动力系数突降的风攻角下，尾流中的轴向流不是非常明显，轴向流对于干索驰振的影响值得进一步定量研究。

斜拉索； 干索驰振； 数值模拟； 风洞试验； 机理

斜拉索质量轻、频率低、阻尼小，极易在风荷载的作用下发生大幅振动。在斜拉索各种风致振动中，风雨激振是危害最大的一种。风雨激振是斜拉索在风和雨共同作用下发生的一种大幅、低频振动，自20世纪80年代以来，研究者对其机理进行了大量的研究[1-3]，研究结果表明：斜拉索表面形成的上水线对风雨激振的起振关系密切。与此同时，人们也发现，在有风无雨的情况下，斜拉索也会发生大幅振动。对于这种类型的拉索振动，主要有两种解释：第一种是高风速下的涡激共振，主要由日本学者Matsumoto等[4]提出；第二种是干索驰振(Dry galloping)，与平均气动力系数的突降有关。Chen等[5]进行了三维斜索节段模型测振试验，在试验室中重现了干索弛振现象；Chen等[6]则在对斜索表面进行刚性模型测压的基础上，通过积分得到了斜索的平均气动力系数，研究结果表明：在特定的倾角和风攻角下，平均升力系数确实会出现突降；Matsumoto等[7]认为轴向流对干索驰振有重要影响，且与雷诺数从亚临界区向临界区过渡有关；刘庆宽等[8]对二维拉索进行测力试验发现，当雷诺数进入临界区域时，会产生较大的平均升力。

本文采用FLUENT软件平台的LES模块，对直索和斜索进行数值模拟，并在风洞实验室中进行了PIV风洞试验。研究了直索和斜索表面风压系数、平均气动力系数、气动力系数轴向相关性、尾流特性等，在此基础上，对干索驰振机理进行了一定的解释。

1 数值模型

斜拉索空间姿态采用倾角α和风攻角β来定义，如图1所示。拉索直径D取为150 mm。数值模拟对象包括两种：直索和斜索。对于直索模型，计算流域的长、宽、高分别为34D、6D和20D，如图2(a)所示。其中，拉索中心线与计算流域上、下表面的距离均为10D，与入口的距离为10D，与出口的距离为24D。对于斜索模型，拉索上、下端点与计算流域上、下表面的距离分别为10D，拉索前、后端点与计算流域的入口、出口的距离分别为10D、24D，如图2(b)所示。入口采用速度边界条件；出口采用压力边界条件；上、下表面采用对称边界条件；左、右表面采用自由滑移壁面条件；拉索表面采用无滑移壁面条件，如图3所示。

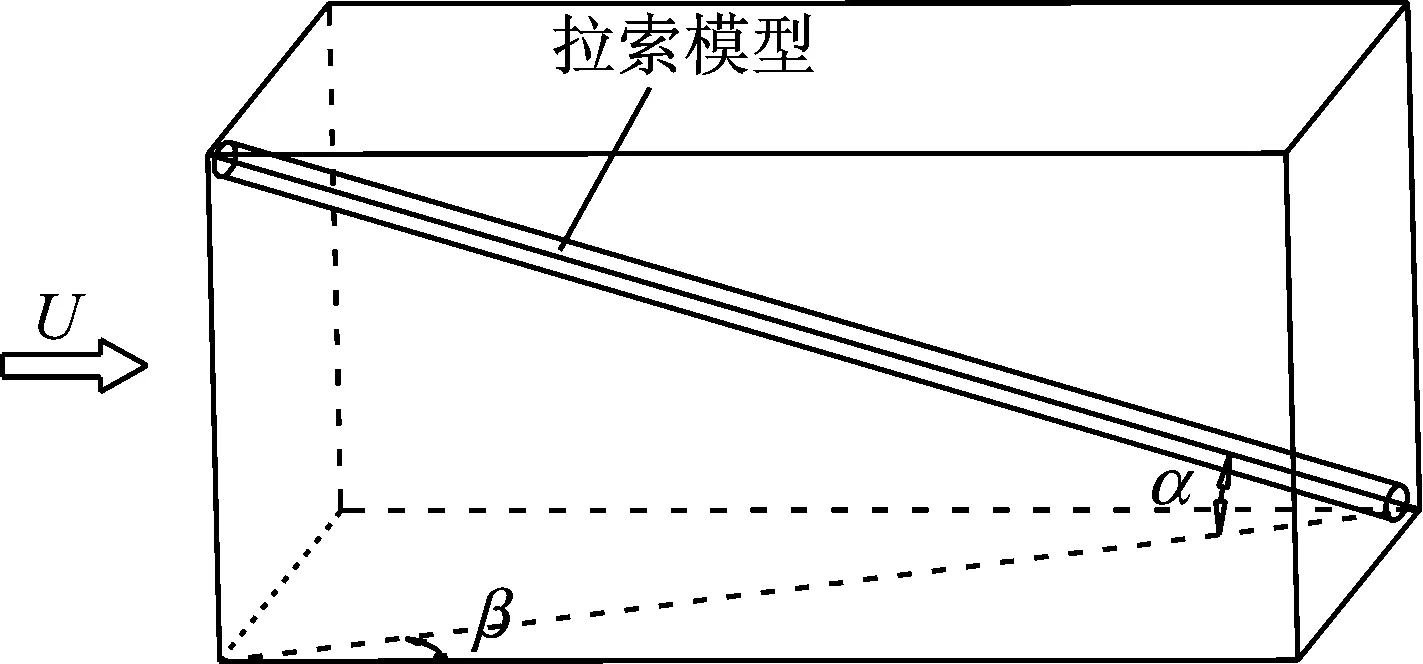
图1 拉索的空间姿态

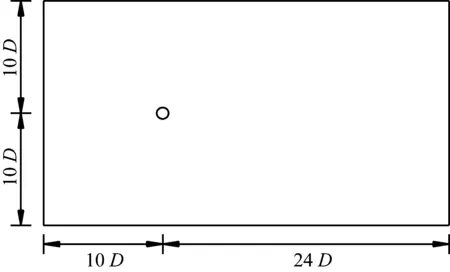
(a) 直索模型

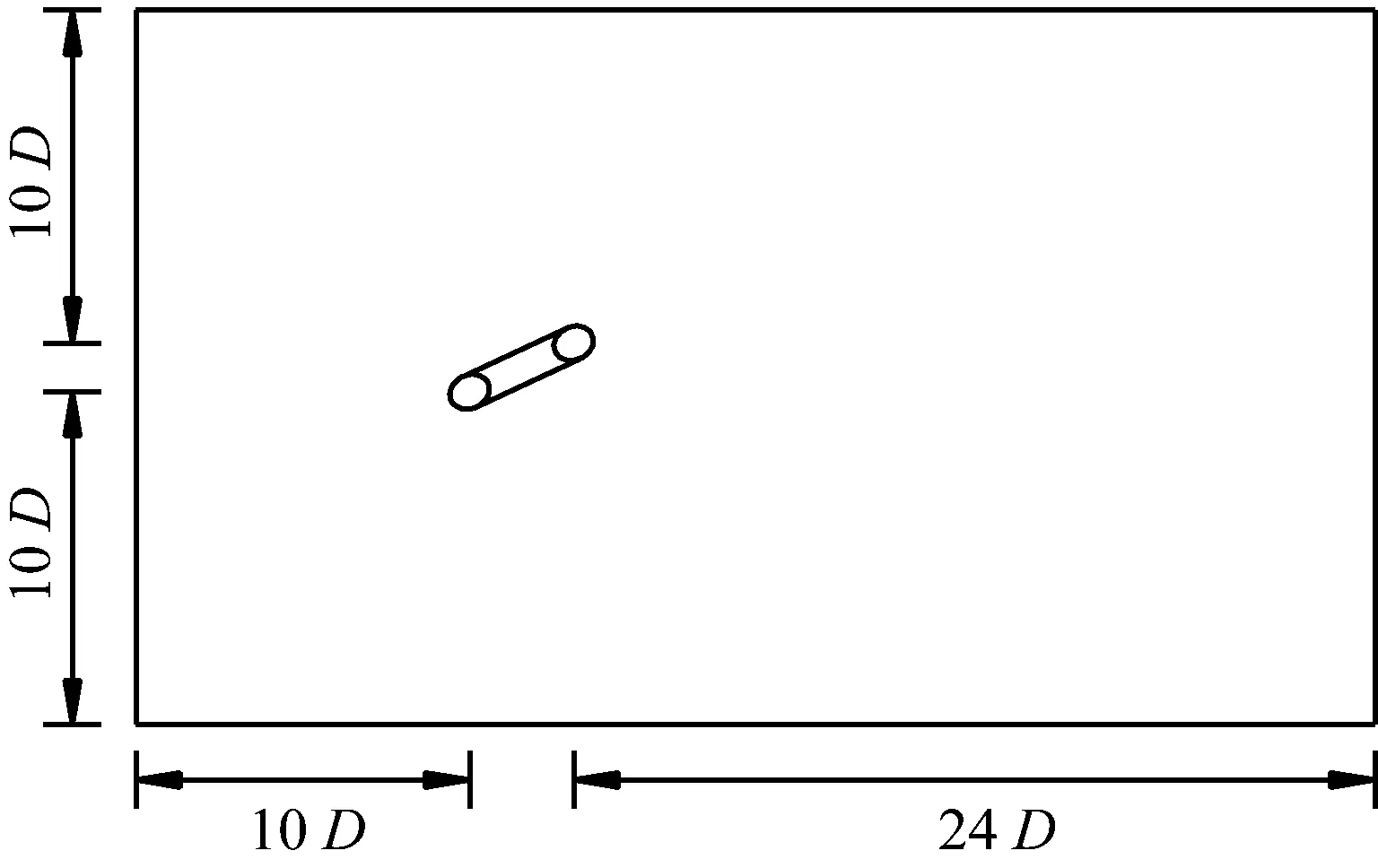
(b) 斜索模型

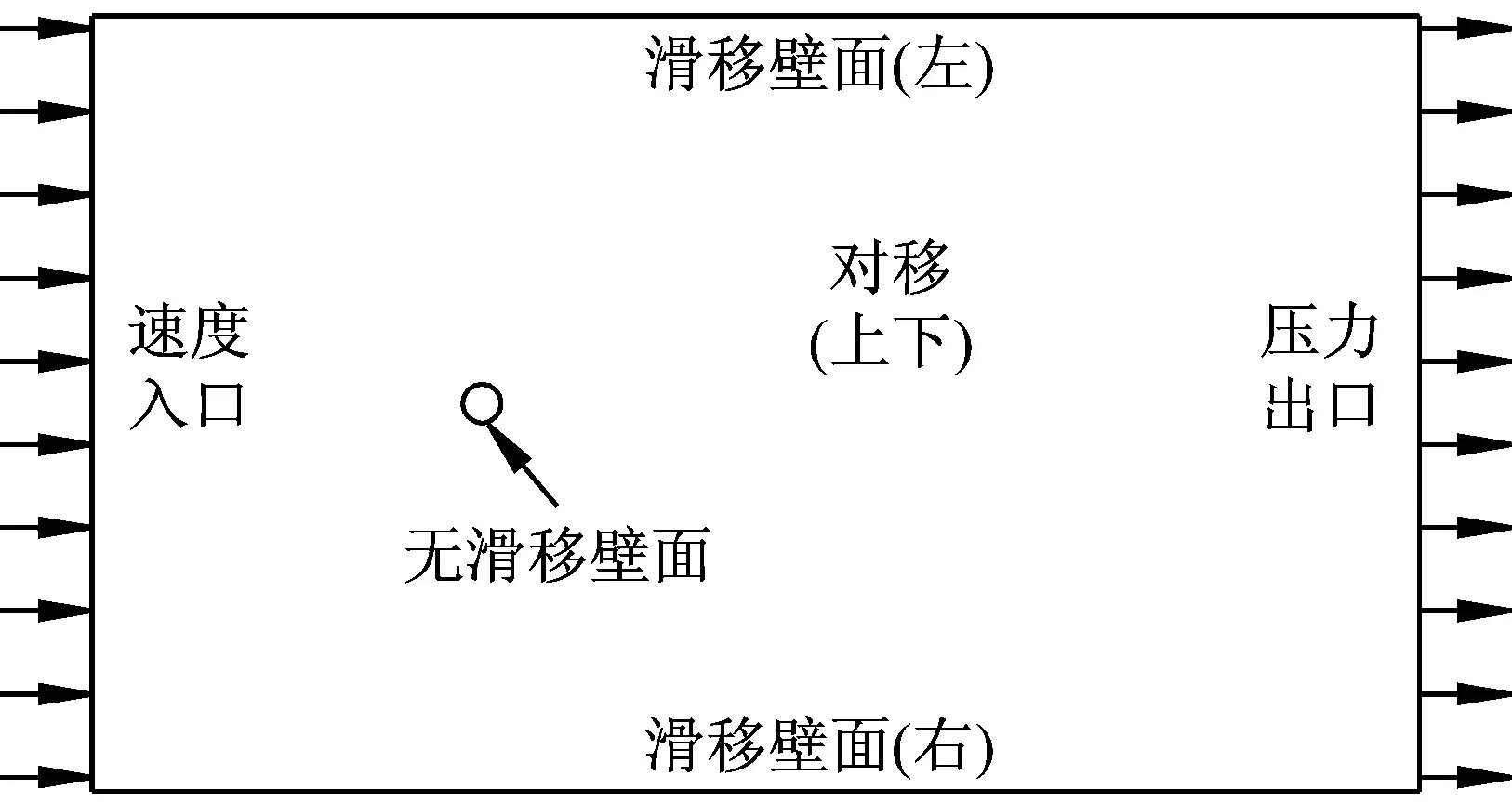
(a) 直索模型

(b) 斜索模型

在拉索表面设置7个截面的风压监测点，每个截面与拉索轴线方向垂直，相邻截面的间距为0.1 m，其中截面4为拉索的中间截面。每个截面上共均匀布置风压监测点36个，相邻监测点的圆心角为10°，如图4所示。

网格划分对数值模拟结果的影响很大。采用结构化网格进行网格划分，为保证计算精度，第一层网格的无量纲高度y+保持在0.30以下，直索和斜索模型的网格总数分别约为44万和60万，并进行了网格收敛性验证。拉索截面附近的网格，如图5所示。从图5中可以看出，在与来流平行的竖截面内，直索的截面是圆形，而斜索的截面是椭圆形。

直索模拟工况只有1个；斜索的倾角α为55°，风攻角β在0°～60°之间，基本间隔5°，在25°～35°之间加密至1°，斜索工况总数为21个。来流采用均匀流，风速为30 m/s和50 m/s，对应的雷诺数分别为3.0×105和5.0×105。

2 PIV风洞试验

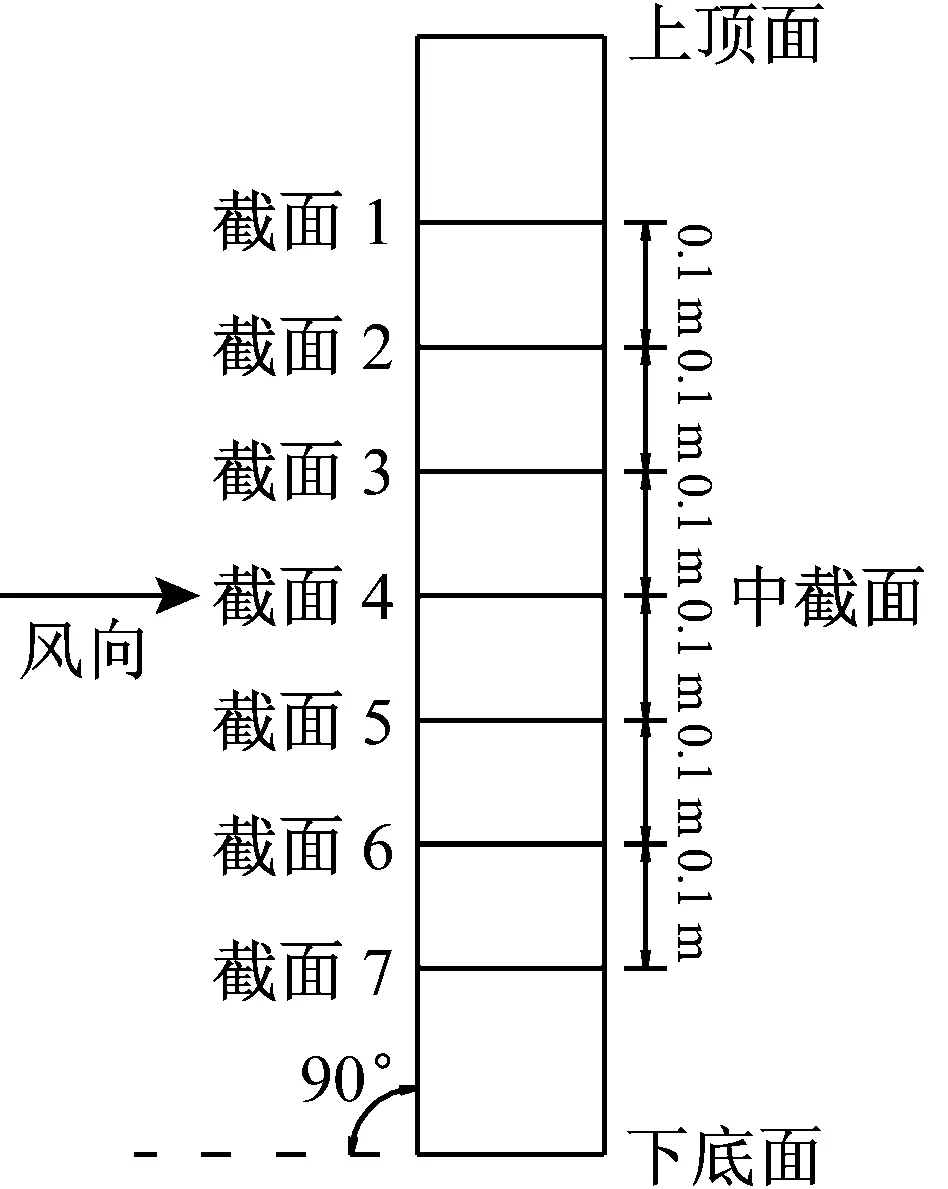
(a) 直索

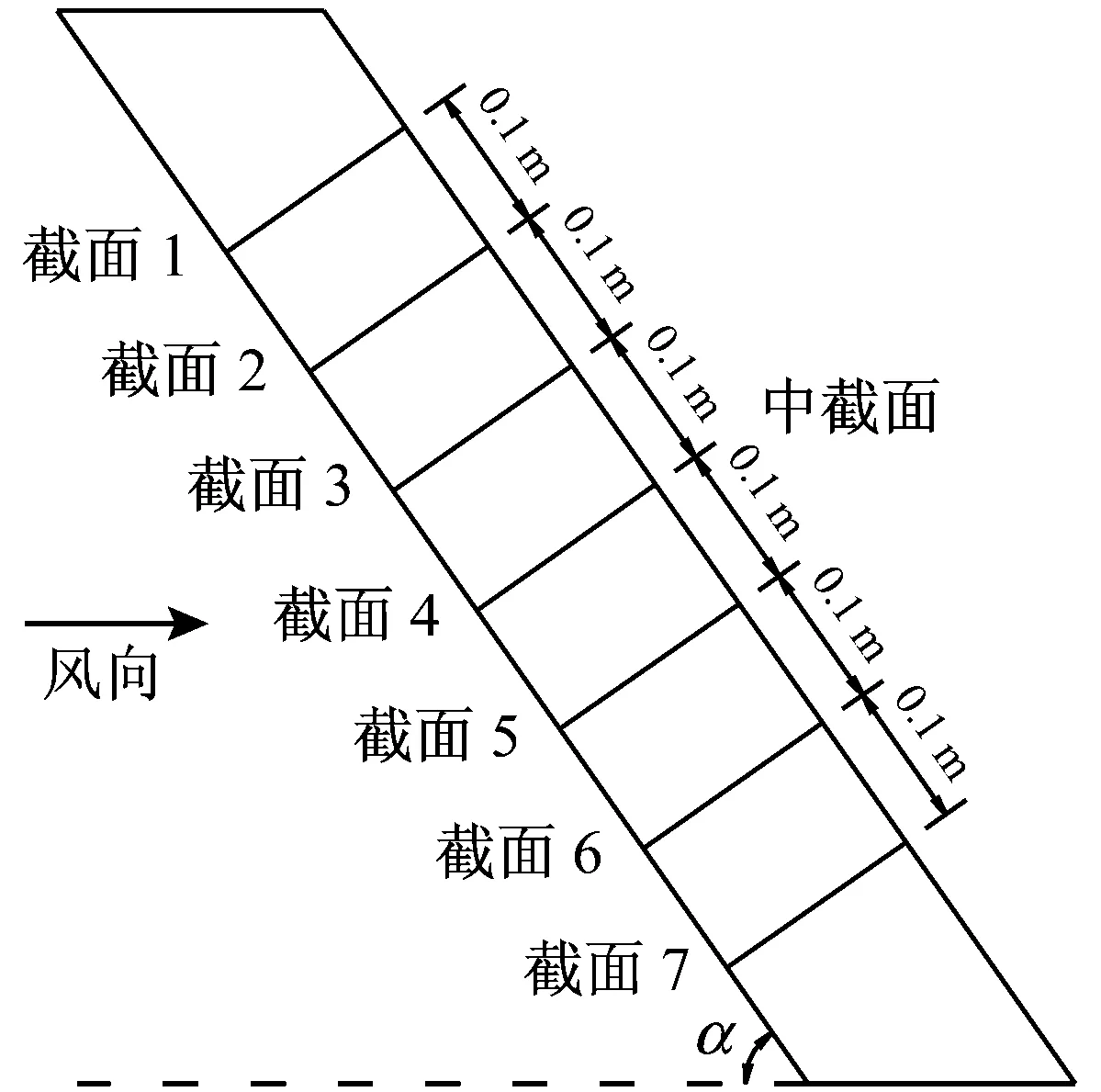
(b) 斜索

(c) 截面测点

(a) 直索

(b) 斜索

粒子图像测速法(Particle Image Velocimetry, PIV)是一种瞬态、多点、无接触式的流体力学测速方法，能在同一瞬态记录下大量空间点上的速度分布信息，并可提供丰富的流场空间结构以及流动特性。试验在湖南大学风工程试验研究中心HD-2大气边界层风洞实验室的高度试验段进行。该试验段长17 m、宽3 m、高2.5 m，最高风速可达58 m/s。拉索模型直径150 mm，与数值模拟相同。拉索长度为1 500 mm，其固定装置及风向角定义如图6所示，试验中主要采集拉索轴线的竖直平面内的风速数据。试验在均匀流场中进行，风速为30 m/s。拉索倾角固定为55°，风攻角与数值模拟工况相同，风攻角通过转动转盘来实现。

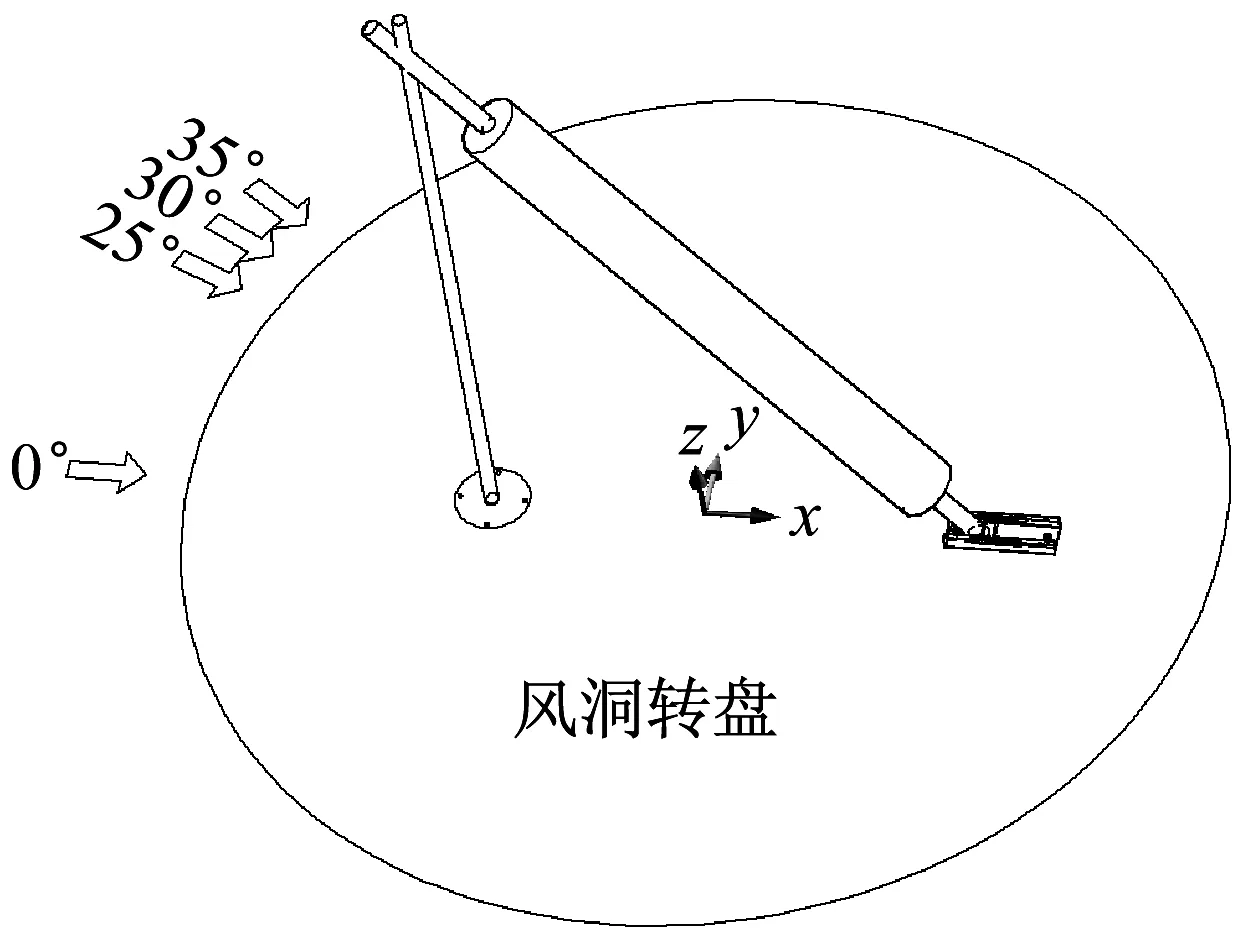
图6 拉索模型装置示意图

3 结果及讨论

模型监测截面气动力的轴向相关系数γxy定义如下：

(1)

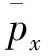
3.1 平均风压系数

数值模拟结果表明：7个截面的平均和脉动风压系数结果非常一致，后文仅分析中间截面结果。图7给出了直索模型中间截面的平均风压系数与文献结果的比较，包括Achenbach[9]的风洞试验结果(Re=5.0×105)、Catalano等[10]的数值模拟结果(Re=1.0×106)。从图7中可以看出，在气流分离区附近，平均风压系数有一定的差异，但总体上来说，本文的平均风压系数结果与文献结果吻合较好。图8给出了风攻角β=0°、10°、20°、30°时斜索模型中间截面的平均风压系数周向分布规律。从图8中可以看出，与直索模型相比，驻点处的平均风压系数约为0.7左右，小于直索模型的1.0，这主要是因为来流和拉索表面不垂直，一部分风速能量分解到与拉索表面相切的方向上；另外，分离点和背风面的风压吸力也小于直索模型的值。斜索平均风压系数的这些特点与文献[11]的结果吻合较好。

图7 平均风压系数结果的验证

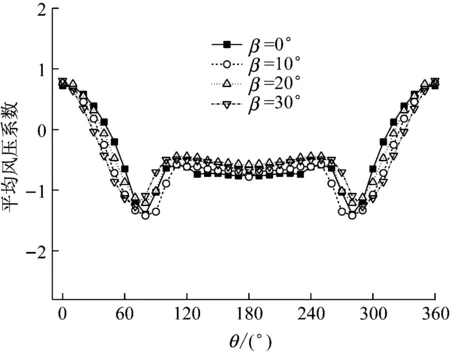
图8 斜索的平均风压系数(Re=3.0×105)

3.2 气动力系数

雷诺数为3×105时，直索模型的平均阻力系数为0.88，脉动升力系数的根方差值为0.40，这与经典结果比较吻合[12]。与直索模型不同的是，斜索模型的平均气动力力系数随着风攻角的变化而变化。图9给出了斜索模型的平均阻力系数和平均升力系数随风攻角的变化曲线，包括雷诺数为3×105和5×105。从图9中可以看出，平均升力系数在25°～32°之间出现了较大的突降，这将使得平均升力系数对风攻角的导数为负值。根据经典的Denhartog驰振理论[13]，若驰振力系数小于零，即：

(2)

则表示气流和结构的相互耦合作用会引起负的气动阻尼，从而使得结构发生剧烈振动。图10给出了根据图9的平均气动力系数得到的驰振力系数。从图10中可以看出，两种雷诺数情况下，驰振力系数均在β=25°～32°范围内出现较大的负值，其中，雷诺数为3×105时，最大负驰振力系数达到-3.85；雷诺数为5×105时，最大负驰振力系数达到-4.74。因此，从平均气动力系数的特点来看，斜索确实存在发生驰振的可能性。需要说明的是，图9和图10的结果是拉索倾角α=55°情况下的值，拉索倾角变化，平均气动升力突降的风攻角范围及其对应的驰振力系数大小也会发生变化。从图5(b)中可以看出，在斜风作用下，拉索的迎风截面为椭圆形，且随着风攻角的变化迎风椭圆截面也会变化，这应该是斜索平均升力系数发生突降的主要原因。

3.3 气动力系数的轴向相关性

图11和图12分别给出了雷诺数为3×105时、直索和斜索各个截面与中间截面气动力系数之间的相关系数，其中拉索截面的气动力系数通过监测点风压积分得到。从图11中可以看出，直索各截面气动力系数之间的相关性较好，且均呈现为正相关，截面1、2、3与截面4之间阻力系数的相关系数分别为0.27、0.46、0.47，对应的升力系数的相关系数分别为0.55、0.74、0.86，升力系数的相关性高于阻力系数的相关性。从图12中可以看出，斜索各截面气动力系数之间的相关性要小于直索的值，其中阻力系数的相关系数主要为正相关，但升力系数的相关系数出现了较大的负值，特别是在风攻角β=20°～35°范围内，截面3和截面4的升力系数的负相关系数可达到-0.60左右，这说明斜索表面的气动力时空分布比直索更为紊乱。

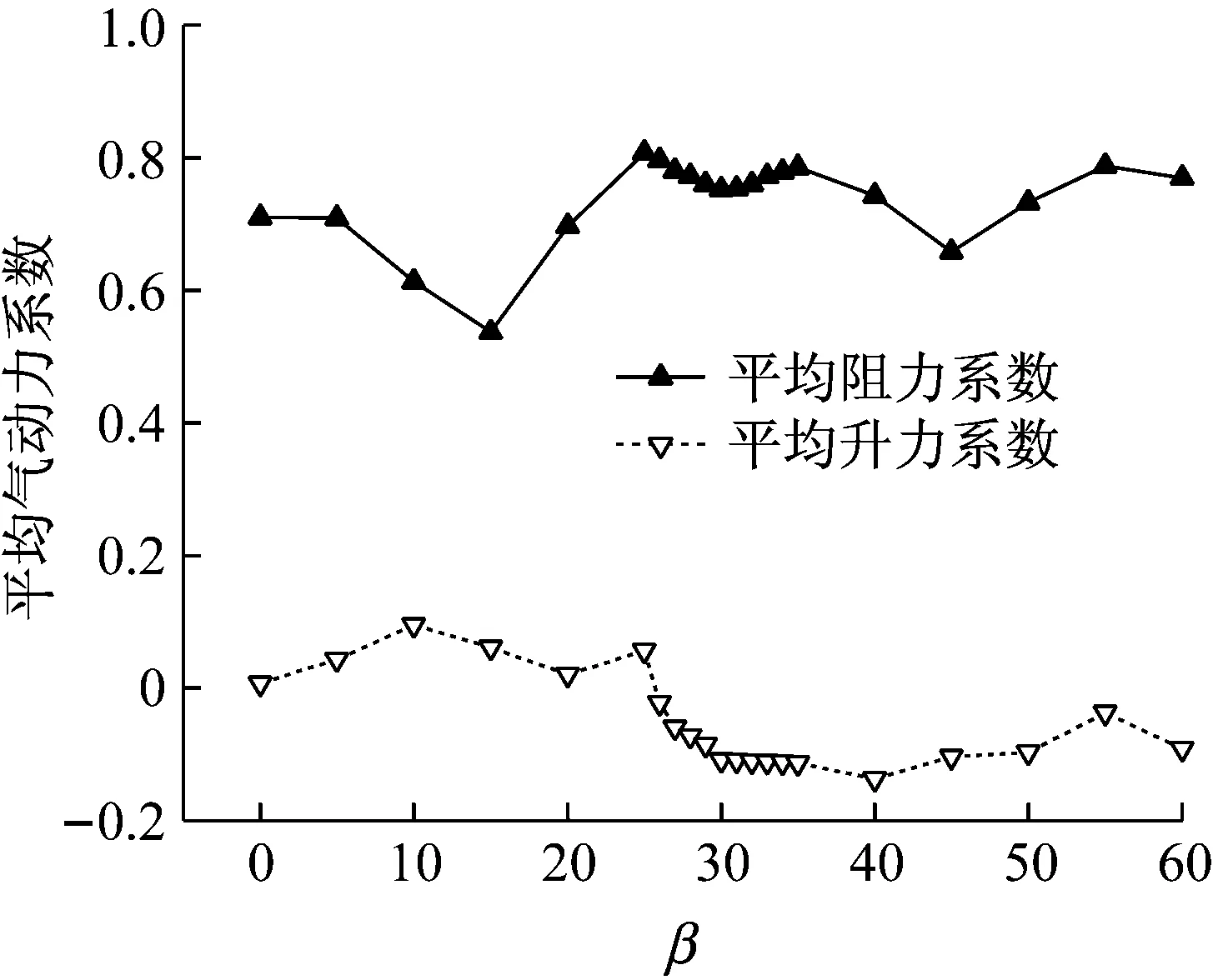
(a) Re=3.0×105

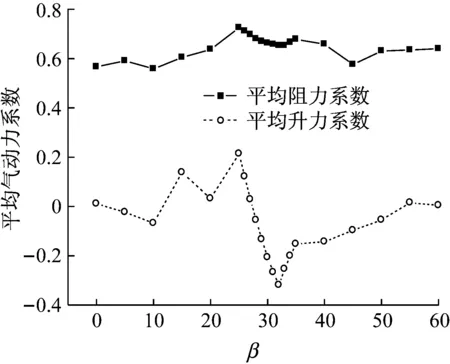
(b) Re=5.0×105

3.4 尾流特征

图10 斜索的驰振力系数

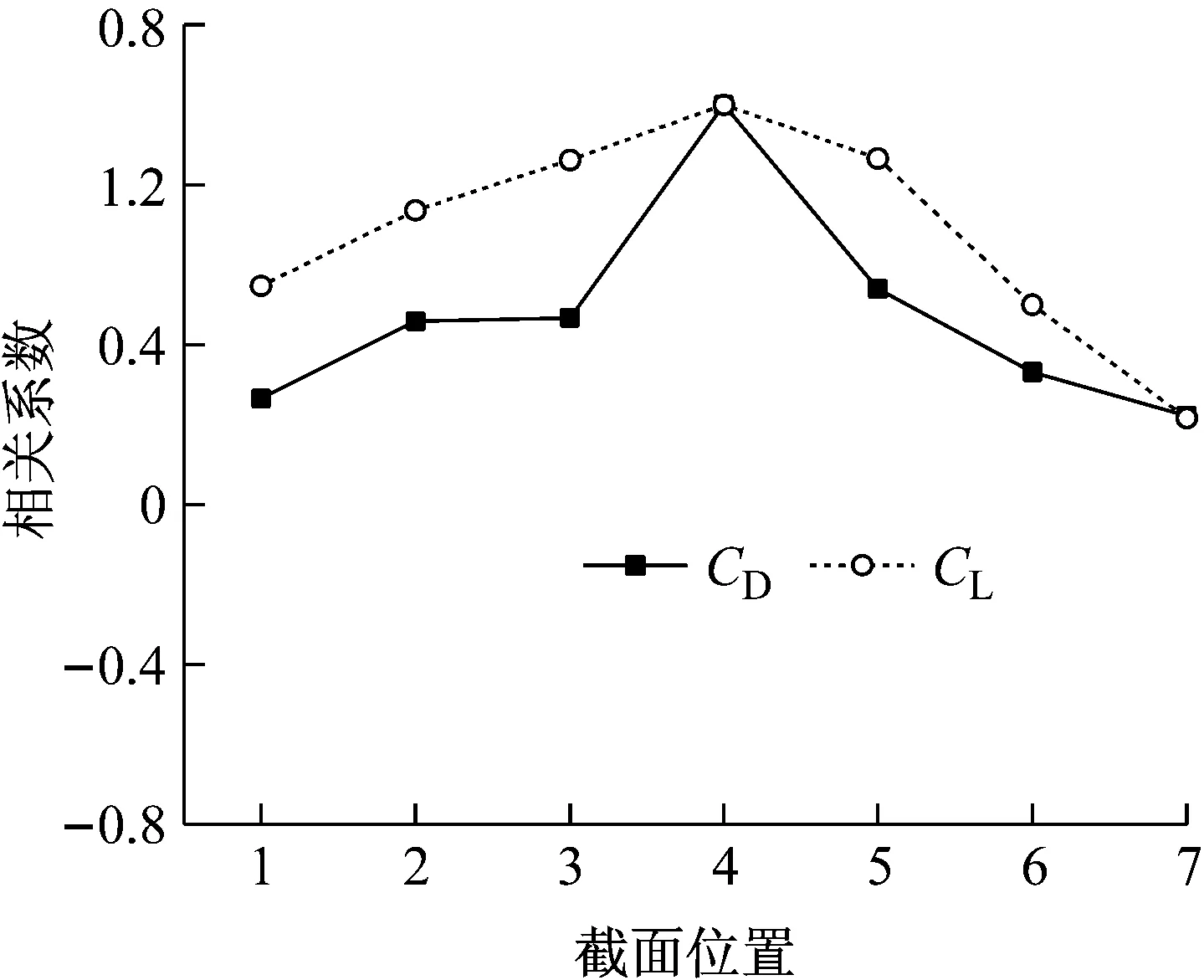
图11 直索各截面气动力系数的相关系数(Re=3.0×105)

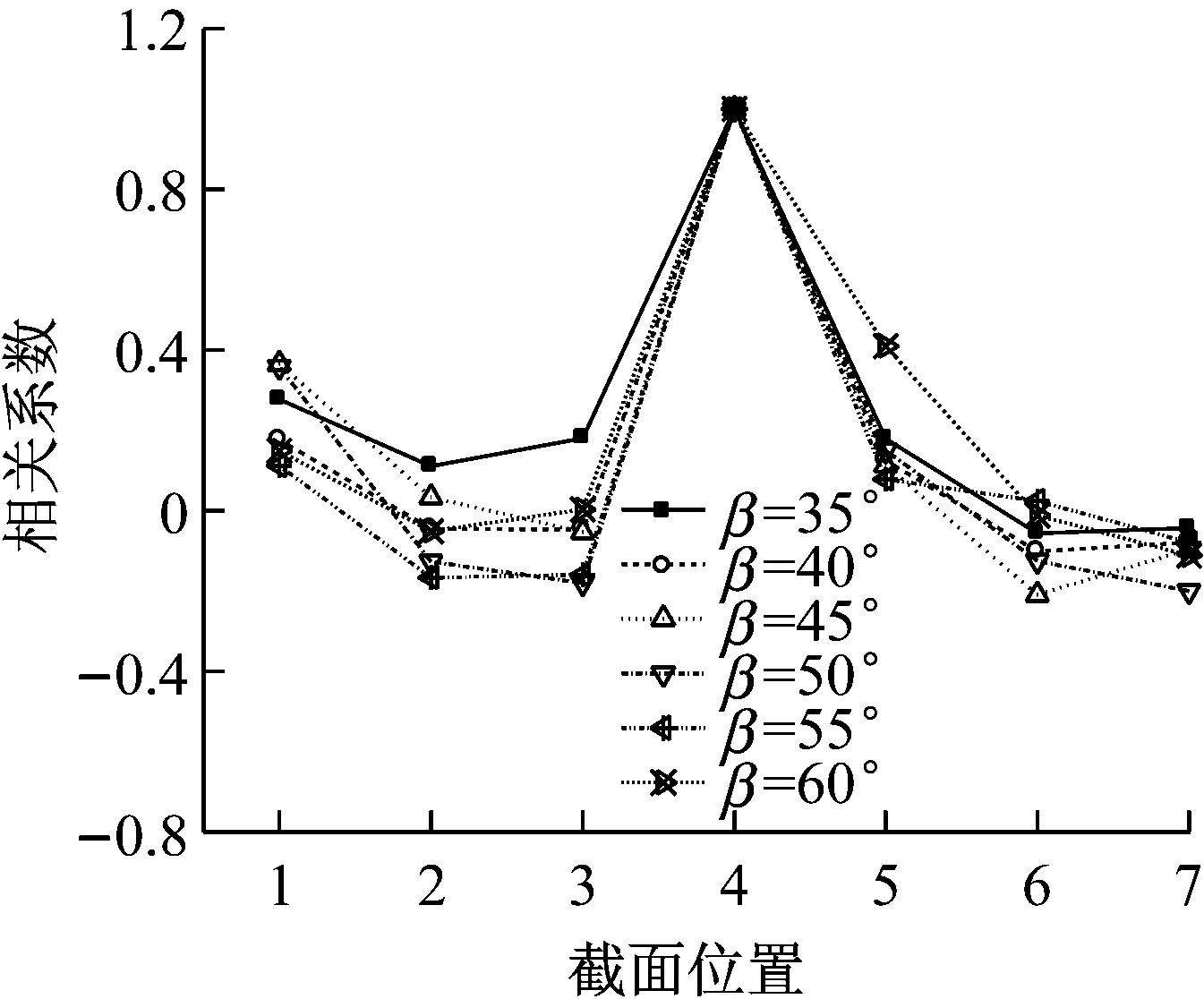
(a) 阻力系数

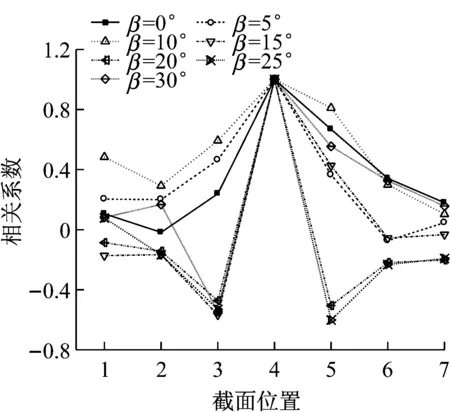
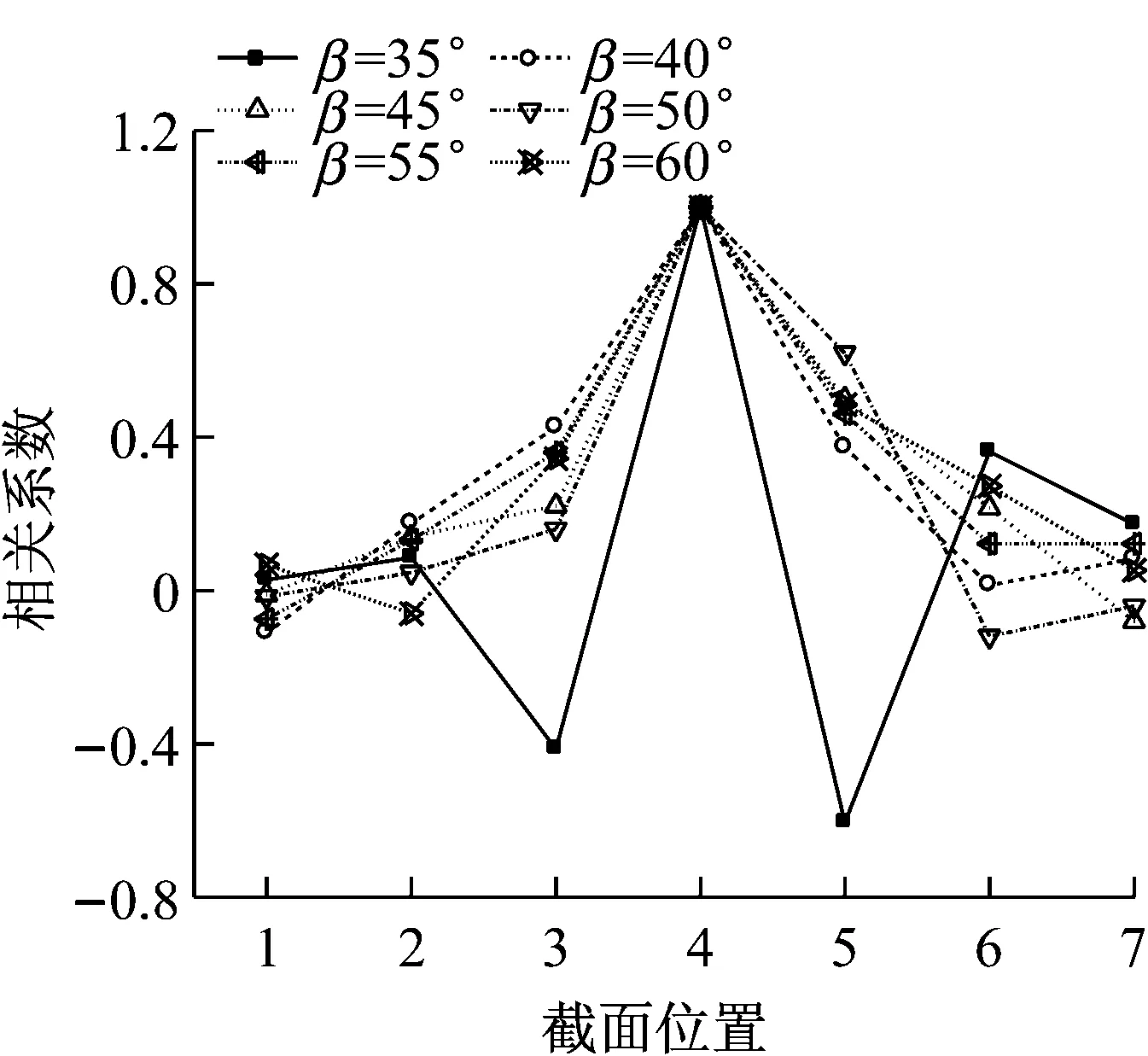
(b) 升力系数

图13给出了通过PIV成像风洞试验得到的斜索尾流的流线图及速度云图，其中，风攻角β=0°、25°、30°、35°，雷诺数Re=3×105。图13中同时还给出了通过CFD数值模拟得到的流线图。从图14中可以看出，在风攻角β=0°、25°时，斜索尾流的轴向流分量非常明显，但随着风攻角的增大(当β=30°、35°时)，轴向流分量有减小的趋势。日本学者Matsumoto认为轴向流是引起干索驰振的一个重要原因[7]，从本文数值模拟结果来看，负驰振力系数的风攻角范围内(β=25°～32°)，轴向流并不明显，轴向流对于干索驰振的影响需进一步的定量研究。值得注意的是，从数值模拟得到的流线图可以发现，当风攻角β=20°～35°时，存在两个方向的轴向流，并交织在一起。

4 结 论

对直索和斜索模型进行了CFD数值模拟，并在风洞中进行了斜索的PIV成像风洞试验，得到如下主要

(a) β=0°

(c) β=30°

(d) β=35°

图13 斜索尾流的流线图(Re=3.0×105)

Fig.13 Streamline in the wake of the 3-d cable (Re=3.0×105)

结论：

(1) 斜索倾角为55°、风攻角在25°～32°范围内时，斜索的驰振力系数出现负值，最大负驰振力系数可达到-4.74，这表明斜索有发生干索驰振的可能性，主要原因可能为斜索迎风截面变为椭圆形。

(2) 斜索轴向气动力的相关系数远小于直索的轴向气动力相关系数，且升力的轴向相关系数大于阻力的轴向相关系数。当风攻角为20°～35°范围内时，斜索升力的轴向相关系数为较大的负值。

(3) 从PIV成像风洞试验结果来看，当斜索倾角为55°时，风攻角为0°和25°时的轴向流非常明显，但当风攻角为30°和35°时，尾流的轴向流分量减弱，轴向流的作用值得进一步定量研究。

[1] HIKAMI Y, SHIRAISHI N. Rain-wind induced vibrations of cables in cable stayed bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 29: 409-418.

[2] GU M, DU X Q. Experimental investigation of rain-wind-induced vibration of cables in cable-stayed bridges and its mitigation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93: 79-95.

[3] LI S Y, CHEN Z Q, WU T, et al. Rain-wind-induced in-plane and out-of-plane vibrations of stay cables[J]. Journal of Engineering Mechanics, 2013, 39(12): 1688-1698.

[4] MATSUMOTO M, SHIRATO H, YAGI T, et al. Field observation system of cable aerodynamics in natural wind[J]. In: Proceedings of the Fourth International Symposium on Cable Dynamics, Montreal, Canada, 2001: 219-225.

[5] CHENG S, LAROSE G L, SAVAGE M G, et al. Experimental study on the wind-induced vibration of a dry

inclined cable—Part I: Phenomena[J]. Journal of wind engineering and industrial aerodynamics, 2008, 96: 2231-2253.

[6] CHENG S, IRWIN P A, TANAKA H. Experimental study on the wind-induced vibration of a dry inclined cable--Part II: Proposed mechanisms[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 2254-2272.

[7] MATSUMOTO M, YAGI T, HATSUDA H, et al. Dry galloping characteristics and its mechanism of inclined/yawed cables[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(6): 317-327.

[8] 刘庆宽，张峰，马文勇，等.斜拉索雷诺数效应与风致振动的试验研究，振动与冲击，2011, 30(12): 114-119.

LIU Qingkuan, ZHANG Feng, MA Wenyong, et al. Tests for Reynolds number effect and wind-induced vibration of stay cables[J]. Journal of Vibration and Shock, 2011, 30(12): 114-119.

[9] ACHENBACH E. Distribution of local pressure and skin friction around a circular cylinder in cross flow up toRe= 5×106[J]. Fluid Mech, 1968, 34(4):625-39.

[10] CATALANO P, WANG M, IACCARINO G, et al. Numerical simulation of the flow around a circular cylinder at high Reynolds numbers[J]. Int. J. Heat Fluid Flow, 2003, 24: 463-469.

[11] 李寿英，顾明.斜、直圆柱绕流的CFD模拟[J].空气动力学学报，2005, 23(2): 222-227.

LI Shouying, GU Ming. Numerical simulation for flow around perpendicular and oblique circular cylinders[J]. Acta Aerodynamica Sinica, 2005, 23(2): 222-227.

[12] SCHLICHTING H, GERSTEN K. Boundary-laryer theory[M]. New York: McGraw Hill, 1979.

[13] DENHARTOG J P. Mechanical Vibrations[M]. New York: Dover Publications, INC., 1985.

Numerical simulations and tests for dry galloping mechanism of stay cables

LI Shouying, ZENG Qingyu, WEN Xiaoguang, CHEN Zhengqing

(Key Laboratory for Wind and Bridge Engineering of Hunan Province, Hunan University, Changsha 410082, China)

The dry galloping mechanism of stay cables was studied by means of CFD simulations and wind tunnel tests. Firstly, CFD simulations with 2-D and 3-D cable models were conducted by utilizing the LES method based on FLUENT software to obtain wind pressure coefficients, mean drag and lift coefficients, correlation coefficients of fluctuating aerodynamic forces along the cable axis. Secondly, wind tunnel tests using the particle image velocimetry (PIV) technique were performed to specially investigate characteristics of stay cable wake flow. The results showed that a sudden decrease in mean lift coefficient of a 3-D stay cable is observed, and a maximum minus galloping force coefficient -4.74 is found, so large amplitude galloping vibration of the stay cable is possible to take place; correlation coefficients between aerodynamic forces of a 3-D cable’s cross sections are smaller than those of a 2-D cable, and correlations of drag coefficients are smaller than those of lift coefficients; the axial flow in a 3-D cable’s wake flow is not very obvious; the effects of axial flow on cable galloping vibration need further quantitatively studying.

stay cable; dry galloping; CFD simulation; wind tunnel tests; mechanism

国家重点基础研究发展计划(2015CB057701; 2015CB057702)； 国家自然科学基金(51578234)

2015-09-14 修改稿收到日期：2016-04-16

李寿英 男，教授，博士生导师，1977年5月出生

U448.27

A

10.13465/j.cnki.jvs.2017.11.015