Scruton数对小宽高比H型断面典型攻角风致振动的影响
2023-07-10高广中韦立博马腾飞薛晓锋李加武严庆辰
高广中 韦立博 马腾飞 薛晓锋 李加武 严庆辰

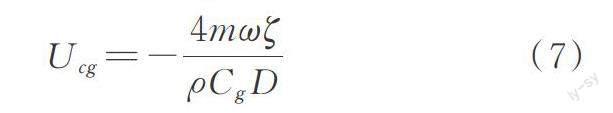
摘要 驰振是一种易发于细长钝体构件的横风向气动失稳现象,质量阻尼参数是影响结构驰振特性的关键参数之一。为探究质量阻尼参数对小宽高比H型断面驰振的影响规律,本研究以曾家岩嘉陵江大桥H型吊杆为工程背景,针对宽高比B/D=1.91的H型断面进行节段模型风洞试验,得到典型风攻角下驰振响应特征,并分别研究了质量、阻尼参数变化所引起的Scruton数变化对大攻角驰振响应的影响规律,探讨了Scruton作为单一参数描述质量阻尼参数影响的可行性。试验结果表明:宽高比B/D=1.91的H型截面在风攻角0°和70°出现非定常大振幅驰振,当Scruton数增大,70°攻角的驰振振幅?风速曲线变化较0°攻角更显著;攻角0°和70°下的驰振临界风速均低于准定常理论值,采用经典准定常理论预测结果偏于危险,0°攻角相较70°攻角的起振风速更低,更容易发生风致振动,并且非定常驰振现象显著;阻尼比和质量比对不同风攻角下驰振的影响不同,在风攻角0°下,两者可近似由Scruton数统一表示,但在大攻角70°下,不能简单地由Scruton数表示。
关键词 驰振; 细长结构; H型断面; 风洞试验; Scruton数; 风攻角
引 言
近年来,随着桥梁建造技术的进步以及新材料的应用,中国桥梁结构正朝着大跨、轻柔的方向发展。H型吊杆作为大跨拱桥和钢桁架桥的关键构件,具有长细比大,阻尼比小的特点。与水平放置的桥梁主梁不同,竖向安装的H型吊杆可能受到风向角0°~360°的影响,需要检验大风向角下的风振性能,这也对抗风性能提出了更高要求。相比于圆形截面的吊杆,钝体H型截面气动性能更差,更容易在常遇风速下出现各种风致振动问题,甚至发生破坏。
驰振是细长柔性结构在横风向出现的一种发散性自激振动,一旦超过驰振临界风速,其振幅会随着风速增加而增大[1]。横风向驰振失稳主要是由钝体断面前缘拐角发生流动分离形成的尾流与结构的相互作用引起的,顺风向的尺寸B与迎风面高度D的比值B/D是重要的影响因素之一[2?4]。Parkinson[5]发现在均匀流下,当钝体断面的宽高比B/D在0.75~3范围内,涡激振动的干扰很容易产生横风向驰振;当B/D在0.75~2范围内,在迎风侧前缘发生交替分离产生的尾流会导致涡激振动和驰振[6]。
已有大量文献对H型吊杆在不同攻角下的驰振特性进行了深入研究:马存明等[7]通过风洞试验,综合评价了不同截面形式的H型吊杆的涡振和驰振特性,认为H型吊杆的风致振动主要表现为驰振。文献[8?10]利用风洞节段模型试验,研究了0°~90°风偏角下不同宽高比和腹板开孔率的驰振性能,发现B/D=2.4的H型吊杆在0°~8°,64°~90°风偏角存在两个失稳区间,其中0°和5°风偏角会发生明显驰振,起振风速偏低,并且宽高比改变不能有效改善H型吊杆的驰振特性。
临界风速与质量阻尼参数(Scruton数)的关系图于1960年由Scruton首次提出[11]。之后,准定常理论成功预测了各类钝体结构发生驰振时的临界风速和临界状态。该理论仅适用于高约化风速下的驰振,即旋涡脱落频率远大于结构自振频率,涡激脱落的影响可以忽略[12]。当驰振起振风速接近甚至低于涡振起振风速时,驰振和涡振会发生相互影响,经典的驰振准定常理论不再适用。准定常理论不仅会高估驰振起振风速,还可能低估振幅响应,对于设计有可能是偏危险的[13]。Mannini等[14]说明了在準定常框架下,B/D在1~2之间矩形断面驰振问题的复杂性和研究的必要性。低Scruton数下常出现不能明确区分驰振与涡振的现象,为了使B/D=1.5矩形断面的涡振和驰振的范围完全解耦,准定常理论准确预测驰振临界风速,需要较大的质量阻尼参数值[15]。不同结构的质量、阻尼参数对振幅的影响不相互独立,不能仅由一个参数Scruton数决定动力响应[16?17]。周帅等[18?19]通过风洞试验实测B/D=1.2的矩形断面,发现涡振幅值响应随着阻尼、质量的增大而减小,并且质量参数敏感性权重大于阻尼参数。但在涡振和驰振耦合状态下,振动响应对质量、阻尼参数的变化不敏感。
综上,前期针对钝体断面驰振的研究主要集中在矩形断面,H型断面的风振性能研究主要集中在较大宽高比,对于较小宽高比(B/D<2)的风振特性研究仍然比较匮乏,特别是大攻角和质量阻尼参数的影响规律仍须详细探讨。本文以曾家岩嘉陵江大桥H型吊杆为工程背景,通过节段模型风洞试验研究了小宽高比H型断面在大攻角下的驰振响应,并揭示了质量和阻尼参数对横风向驰振的影响规律。
1 风洞试验
1.1 试验模型及装置
节段模型试验在长安大学风洞实验室CA?1大气边界层风洞中进行。试验段横截面宽3.0 m,高2.5 m,如图1所示。节段模型以曾家岩嘉陵江大桥的H型吊杆为原型,由轻质铝合金方管和轻质泡沫组成,模型截面宽度B=180 mm,高度D=94 mm,壁厚δ=15 mm,宽高比B/D=1.91/1(如图2所示),节段模型长L=1.5 m,长宽比L/B=8.3>3,0°攻角下的阻塞率为1.88%<5%,满足《公路桥梁抗风设计规范》(JTG/T 3360?01—2018)的要求。
图3为风洞内弹簧悬挂系统安装示意图。结构阻尼采用一种新型试验阻尼调节装置,包括刚性绝缘杆、金属片、电磁铁、滑动变阻器、电源,通过闭合导体铜片切割磁感线运动,可以线性连续独立调节结构竖向和扭转阻尼比,并且与传统的钢丝圈阻尼器相比,不引入附加刚度和非线性效应[20]。模型质量通过吊臂上的质量块连续调节,模型刚度依靠弹性支承在风洞内的弹簧悬挂系统上的8根弹簧提供,并通过支架上固定的3个激光位移传感器获取模型在运动过程中的竖弯和扭转位移时程信号。
1.2 工况设置及参数
质量阻尼参数是由结构质量和阻尼共同决定的,影响结构振动幅值响应的关键参数。通常表示为Scruton数(以下简称“Sc数”):
式中 m为结构每延米等效质量;ζ为结构阻尼比;ρ为空气密度;D为迎风面高度;B为横截面宽度。
描述模型质量参数的变量——质量比:
通过调整质量块使节段模型系统的质量比m*分别为328,446,578,708和836五个不同等级,竖弯阻尼比分别为0.583%,0.792%,1.092%和1.468%四个不同等级,通过质量比、阻尼比参数的组合实现了A1~A4和B1~B4共计8个试验工况。试验研究工况及参数如表1所示。
节段模型试验在均匀流场进行,风攻角在0°~90°范围内以10°为单位变化,针对出现驰振现象的风攻角下改变质量阻尼参数。通过不同工况间的对比,可以观察到Sc数在12.01~31.19范围内的驰振响应。同时,也可以观察到当Sc数接近时,质量、阻尼参数分别对驰振幅值响应的影响。
2 试验结果分析
2.1 H型吊杆的风振特性
为了以准定常理论预测结果,对H型节段模型进行了静三分力系数测量,在试验中,节段模型通过一个微型法兰盘固定在五分量杆式天平上,测量了风攻角0°~90°范围内的静力三分力系数:
式中 ρ为空气密度,ρ=1.225 kg/m3;U为均匀流的来流风速,U=13 m/s;L为模型长,L=1.5 m;FD,FL和M分别为节段模型单位长度上受到的气动阻力、升力和扭矩。
静三分力系数测量结果如图4所示,可以发现,不同攻角下升力系数CL的变化最为明显,在10°和65°附近出现了两个极值。由Den Hartog 准则,可得驰振力系数Cg[1]:
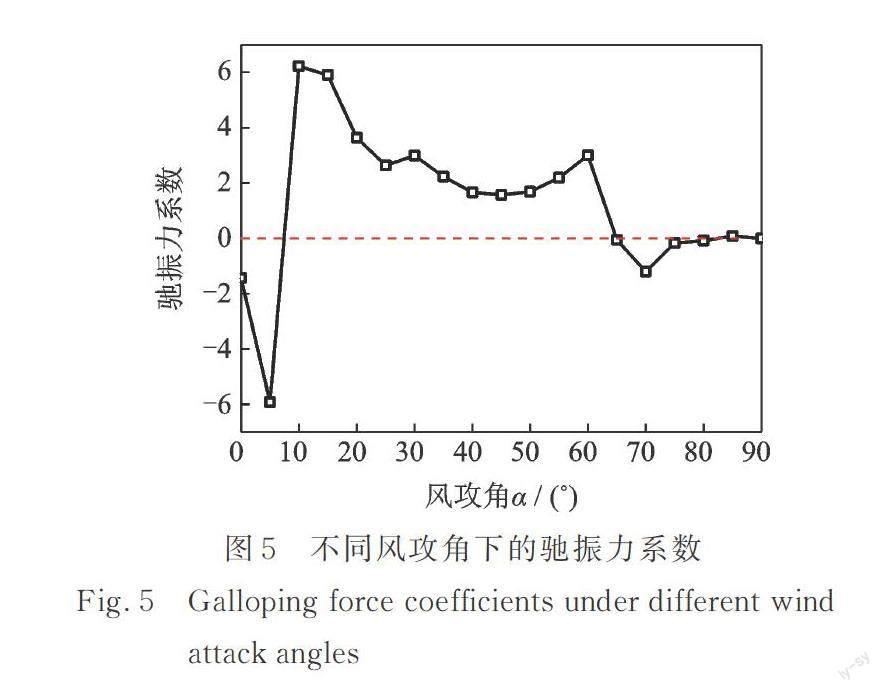
由式(6)计算得到的不同风攻角下的驰振力系数如图5所示,可以看出,宽高比为1.91的H型断面在大多数风攻角范围内驰振力系数均为正值,但在0°,5°和65°~75°风攻角Cg为负值,表明在上述攻角范围内可能发生横风向驰振。
以A1工况为典型工况,通过风洞节段模型测振试验得到该工况下0°~90°的10个风攻角的振动响应。图6给出了各个攻角下的竖向稳态振幅响应随无量纲风速的变化规律(U为风速,y为吊杆稳态振幅值),可以看出,模型在30°和90°攻角下发生了涡振,在0°和70°攻角下发生了驰振,与Den Hartog[1]判据的结果基本吻合,说明该判据在大攻角下仍然具有适用性。
根据准定常理论,当驰振力系数Cg<0时,可以进一步估算驰振临界风速Ucg:
式中 ω为结构一阶弯曲圆频率,ω=2πf。
计算A1~A4和B1~B4工况下,典型攻角驰振临界风速及涡激共振临界风速如表2所示。
2.2 不同Sc数的影响
2.2.1 结构阻尼比的影响
图7为试验所得典型攻角各个工况下的无量纲稳态振幅随约化风速的变化关系。从图7(a)中可以看出,在0°风攻角附近,H型断面质量比相同的情况下增大阻尼比,A1~A3所得无量纲风速?振幅响应曲线曲率接近,起振风速一致且接近涡激共振起振风速Ur*而小于驰振临界风速U*cg,无量纲位移随约化风速增大呈近乎线性变化,是典型的非定常驰振现象[21?22]。表明阻尼比在0.583%~1.092%的范围内涡振和驰振发生了耦合,并且可能存在“锁定区间”,导致A1~A3工况无量纲风速?振幅响应曲线不随阻尼比的大小变化,无量纲风速?振幅响应曲线斜率锁定在0.0218附近。随着阻尼比增大到1.468%,A4工况在较小初始激励的情况下的风振现象为渦振,在超过一定临界值的大激励下表现为驰振,存在振动分叉现象[23]。约化风速U*=22.57时,A4工况振动响应如图8(a)所示,此时当激励振幅小于一定程度时,振动会衰减至平衡位置;当激励振幅大于一定临界值时,振幅会逐渐增加并发展至稳定振幅的极限环振动。风攻角70°下的振动现象有所不同(图7(b))。当阻尼比为0.583%时,起振与涡激共振起振风速Ur*接近且小于驰振临界风速U*cg,模型在约化风速为13.6时振幅达到极值,随后振幅随约化风速增加而近似线性增加。该振动幅值曲线既没有完整的涡振区间,也没有随约化风速发散的驰振现象,是涡振和驰振耦合振动的形式。当阻尼比增大到A2~A4工况,驰振现象消失,仅表现为涡振,并且A4工况中涡振峰值振幅也显著减小。图8(b)为A1工况在约化风速为25.82时的无量纲位移时程曲线,模型在无初始激励的条件下逐渐起振并保持稳定振幅。
2.2.2 结构质量比的影响
图9对比了驰振响应随质量比的变化规律,在0°风攻角A1,B1~B4工况下,约化风速小于12时,质量比越大无量纲振幅越大,当高于20时,质量比越大无量纲振幅越小。所有工况的起振风速相比于准定常理论驰振临界风速都大幅提前,并且接近甚至小于涡振起振风速。质量比越大,模型的实测驰振起振风速越大,如图10(b)所示。在质量比增大到B4工况(m*=836)时,出现了振动分叉现象,说明H型吊杆在0°风攻角下增大质量比可能会改变风致振动现象。
图9(b) 给出了风攻角70°下的试验结果。质量比较小的A1工况,风振响应表现为涡振和驰振耦合。随着质量比增大,驰振临界风速提高,涡振和驰振现象分离,涡振区间随着质量比增大而提前,最大振幅也有减小的趋势。并且发生驰振的无量纲风速?振幅响应曲线斜率基本不变,随着质量比增大向高约化风速平移。当质量比增大至B4工况,与0°风攻角类似,需要足够大的初始激励才表现为驰振。说明在70°风攻角时,增大质量比不但可以避免涡振和驰振的耦合现象,而且可以抑制涡振,延缓甚至抑制驰振。
上述工况的实测驰振临界风速U*rg均低于理论驰振临界风速U*cg(如图10(a)所示),而经典准定常理论适用于高风速驰振,因此,在计算H型吊杆这类钝体断面的低风速非定常驰振临界风速时是偏不利的。实测驰振临界风速向低速区移动,0°攻角相较70°攻角的起振风速更低,更容易发生风致振动。并且0°攻角实测驰振临界风速U*rg与涡激共振起振风速U*r接近,说明非定常驰振现象较70°更为显著。而在70°攻角时,增大阻尼比显然比增大质量比更能降低起振风速。
通过以上结果对比可以看出,在H型吊杆的0°和70°风攻角下,驰振响应随着阻尼比和质量比的变化而变化,且大攻角70°的驰振对阻尼比和质量比更为敏感。
2.3 质量比和阻尼比的影响对比
在0°风攻角不同的对比工况下,Sc数接近时振动现象基本相同(如图11所示)。模型在对比工况1和2均表现为驰振,在对比工况3中表现为振动分叉。说明在Sc数接近的情况下,不同质量和阻尼参数对风致振动响应的影响是类似的。虽然振幅曲线趋势接近(最大相差26%),但三个工况下的振幅响应不完全相同,不同质量比和阻尼比的振幅曲线交叉呈现“X”形。将交叉点处风速定义为“转化风速”,当低于转化风速时,A工况振幅均小于B工况,当高于转化风速则相反,且转化风速随Sc数的增大而增大。说明0°风攻角时在低约化风速区增大阻尼比,在高约化风速区增大质量比,振幅的降低更显著。而针对对比工况3中的振动分叉现象,A4较B4工况的分叉点对应的约化风速更低,无量纲涡振振幅更小,但驰振幅值响应更大。说明在低风速区增大阻尼比对控制涡振更有效,高风速区增大质量比对控制驰振更有效。因此,在0°攻角下,阻尼比和质量比的影响近似由一个无量纲参数——Sc数表示是可行的。
与0°风攻角不同,模型在大攻角下,阻尼比和質量比对驰振的影响存在显著差异,不能简化为Sc数统一表示。如图12所示,在Sc数接近的情况下,不同质量比和阻尼比的组合所得到的风攻角70°下的振动响应是完全不同的。在三个Sc数接近的对比工况中,A工况均表现为涡振,而B工况均为涡振与驰振耦合。说明当Sc数接近时,阻尼比对幅值响应的影响权重要显著大于质量比。但在对比工况1和3中,涡振区间从高约化风速向低约化风速平移,并且对比工况2中涡振幅值也较大,虽然幅值更大的驰振被抑制,但涡振也变为更不利的低风速涡振。因此,针对H型断面在大攻角下振动,用Sc数表示阻尼比和质量比的影响是存在问题的。
需要指出的是,刚性吊杆通常会在腹板或翼板开孔,但对一些受压构件来说,较大开孔率可能会导致构件强度降低甚至失稳破坏。本文旨在得出H型基本钝体断面的风振特性及响应规律,探讨通过调节吊杆质量阻尼参数来控制其风振响应的方法。同时,本文采用的试验方法是传统调整风攻角的方法,即横风向振动沿风轴方向。但在大风攻角下横风向振动方向应为H型吊杆的弱轴方向,传统的弹簧悬挂系统在大攻角下的振动形态可能存在“失真”的问题。因此,未来还应考虑H型截面强轴和弱轴各自的刚度,使得大风攻角下钝体柔性构件三自由度耦合振动测试成为可能[24]。
3 结 论
本文以曾家岩嘉陵江桥H型吊杆为背景,基于宽高比B/D=1.91的H型节段模型开展风洞试验,针对发生驰振的典型风攻角,研究了不同质量阻尼参数对驰振特性的影响。通过试验现象对比分析,Scruton数对H型吊杆模型风致振动行为影响显著。具体可以得到如下结论:
(1) 宽高比B/D=1.91的H型截面在风攻角0°和70°出现非定常驰振。随着Scruton数增大,0°攻角的驰振振幅?风速曲线对Scruton数变化不敏感,振动会在较高的Scruton数下出现振动分叉现象;70°攻角驰振与涡振解耦,驰振起振风速提高,对Scruton数变化更为敏感;
(2) 攻角0°和70°下的驰振临界风速均低于准定常理论值,说明采用经典准定常理论预测结果偏于危险。0°攻角相较70°攻角的起振风速更低,更容易发生风致振动,并且非定常驰振现象显著;
(3) 阻尼比和质量比对不同风攻角下驰振的影响是不同的。在风攻角0°下,两者可近似由Scruton数统一表示,但在大攻角70°下,不同阻尼比和质量比组合得到同一个Scruton数所对应的驰振响应是完全不同的,因此不能简单地由Scruton数表示。
参考文献
1DEN HARTOG J P. Transmission line vibration due to sleet[J]. Transactions of the American Institute of Electrical Engineers, 1932, 51(4): 1074-1076.
2LIAW K F. Simulation of flow around bluff bodies and bridge deck sections using CFD[D]. Nottingham: University of Nottingham, 2005.
3SHIMADA K, ISHIHARA T. Predictability of unsteady two-dimensional k?ε model on the aerodynamic instabilities of some rectangular prisms[J]. Journal of Fluids and Structures, 2012, 28: 20-39.
4WANG S B, CHENG W M, DU R, et al. Unsteady RANS modeling of flow around two-dimensional rectangular cylinders with different side ratios at Reynolds number 6.85×105[J]. Mathematical Problems in Engineering, 2020(3): 2163928.
5PARKINSON G V. Aeroelastic galloping in one degree of freedom [J]. Wind Effects on Buildings and Structures,1963: 582-609.
6TAKEUCHI T, MATSUMOTO M. Aerodynamic response characteristics of rectangular cylinders in tandem arrangement[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41(1-3): 565-575.
7马存明, 廖海黎, 郑史雄, 等. H型截面吊杆气动性能的风洞试验[J]. 中国铁道科学, 2005, 26(4): 42-46.
MA Cunming, LIAO Haili, ZHENG Shixiong, et al. Wind tunnel experiment on the aerodynamic performances of H-shaped booms[J]. Chinese Railway Science, 2005, 26(4): 42-46.
8陈政清, 刘慕广. 腹板开孔的H型吊杆横风向驰振特性试验研究[J]. 湖南大学学报(自然科学版), 2008,35(6): 1-5.
CHEN Zhengqing, LIU Muguang. Experimental study of across-wind galloping of H-shaped hangers with web hole[J]. Journal of Hunan University (Natural Sciences), 2008, 35(6): 1-5.
9刘慕广. 两类大长细比桥梁构件的风振特性研究 [D]. 长沙:湖南大学, 2009.
LIU Muguang. Study on wind-induced vibration characteristics of two classes of bridge components with large slenderness ratio[D]. Changsha: Hunan University, 2009.
10刘慕广, 陈政清. 不同截面参数H型吊杆的气动性能[J]. 工程力学, 2013, 30(5): 221-226.
LIU Muguang, CHEN Zhengqing. Aerodynamic performance of H-section hangers with different sectional parameters[J]. Engineering Mechanics, 2013, 30(5): 221-226.
11SCRUTON C. The Use of Wind Tunnels in Industrial Aerodynamic Research[M]. Advisory Group for Aeronautical Research and Development, 1960.
12PARKINSON G V. Wind-induced instability of structures[J]. Philosophical Transactions of the Royal Society A, Mathematical, Physical and Engineering Sciences, 1971, 269(1199): 395-413.
13PARKINSON G V, WAWZONEK M A. Some considerations of combined effects of galloping and vortex resonance[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1981, 8(1-2): 135-143.
14MANNINI C, MARRA A M, BARTOLI G. VIV-galloping instability of rectangular cylinders: review and new experiments[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 132: 109-124.
15MANNINI C, MARRA A M, MASSAI T, et al. Interference of vortex-induced vibration and transverse galloping for a rectangular cylinder[J]. Journal of Fluids and Structures, 2016, 66: 403-423.
16SARPKAYA T. Fluid forces on oscillating cylinders[J]. Journal of the Waterway, Port, Coastal and Ocean Division, 1978, 104(4): 275-290.
17SARPKAYA T. Hydrodynamic damping, flow-induced oscillations, and biharmonic response[J]. Journal of Offshore Mechanics and Arctic Engineering, 1995, 117(4): 232-238.
18周帥, 罗桂军, 牛华伟, 等. 桥梁吊杆典型风致振动幅值响应质量阻尼效应研究[J]. 振动与冲击, 2021, 40(18): 63-69.
ZHOU S, LUO G J, NIU H W, et al. Mass damping effects for typical wind-induced vibration amplitude responses of bridge hangers[J]. Journal of Vibration and Shock , 2021, 40(18): 63-69.
19ZHOU S, ZOU Y, HUA X, et al. Investigation of the Scruton number effects of wind-induced unsteady galloping responses of bridge suspenders[J]. Shock and Vibration, 2021: 5514719.
20高廣中, 马腾飞, 严庆辰, 等. 一种用于节段模型测试的线性电涡流阻尼器及振动装置: CN 213336710U[P]. 2021-06-01.
GAO G Z, MA T F, YAN Q C, et al. A linear eddy current damper and vibration device for segment model testing: CN 213336710U[P]. 2021?06?01.
21GAO G, ZHU L. Measurement and verification of unsteady galloping force on a rectangular 2:1 cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 157: 76-94.
22GAO G Z, ZHU L D. Nonlinear mathematical model of unsteady galloping force on a rectangular 2:1 cylinder[J]. Journal of Fluids and Structures, 2017, 70: 47-71.
23GAO G Z, ZHU L D, LI J W, et al. Modelling nonlinear aerodynamic damping during transverse aerodynamic instabilities for slender rectangular prisms with typical side ratios[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 197: 104064.
24高广中, 姚博, 李加武, 等. 一种大风攻角下三自由度耦合振动的风洞实验装置: CN 112161774B[P]. 2022-05-06.
GAO G Z, YAO B, LI J W, et al. A wind tunnel experimental device for three?degree?of?freedom coupled vibration under high wind angle of attack: CN 12161774B[P]. 2022-05-06.
Influence of Scruton number on wind?induced vibration of H?section with a small side ratio under large wind angles of attack
GAO Guang-zhong 1 WEI Li-bo 1 MA Teng-fei 2XUE Xiao-feng 1LI Jia-wu 1YAN Qing-chen 1
1. School of Highway, Changan University, Xian 710064, China;
2. China Design Group Co.,Ltd., Nanjing 210006, China
Abstract Galloping is a kind of transverse aerodynamic instability phenomenon to which slender prismatic structures are prone under wind actions, and the mass damping parameter is a key factor in determining the galloping response. The present study aims to explore the influence of the mass damping parameter on the galloping of the H-shaped section with a small side ratio (width-to-depth ratio as B/D=1.91). By taking the H-shaped hanger of the Zengjiayan Jialing River Bridge as the prototype, this study investigates the galloping response under the typical wind attack angles, based on the wind tunnel segmental model test of an H-shaped section with a side ratio B/D=1.91. The effect of the change of Scruton number caused by the mass and damping parameters is then examined on the galloping response under large wind attack angles. Finally, the feasibility of Scruton as a single parameter is discussed to describe the influence of mass damping parameter. The results demonstrate that the H-shaped section with a side ratio B/D=1.91 shows unsteady galloping with large amplitude at the attack angles of 0° and 70°, and compared with 0° attack angle, the change of galloping response at the attack angle of 70° is more sensitive as the Scruton number increases. The onset wind speed of the galloping is, at the attack angles of 0° and 70°, lower than that calculated by the classical quasi-steady theory, which is high and dangerous. Compared with 70° attack angle, the wind-induced vibration at 0° attack angle is more likely to occur due to its lower onset wind speed, and has significant unsteady galloping. The mass ratio and damping ratio have different effects on the galloping at different wind angles of attack. At the attack angle of 0°, the two can be uniformly represented by the Scruton number, but at a large attack angle of 70°, they cannot be accurately represented by the Scruton number. At last, some topics deserving further research are highlighted.
Keywords galloping; slender structures; H-shaped section; wind tunnel test; Scruton number; wind attack angle
