高射速转管炮凸轮曲线槽的优化与设计

李世康，李 强,安俊斌,陈 雷,马 超

(中北大学 机电工程学院，山西 太原 030051)

高射速转管炮凸轮曲线槽的优化与设计

李世康，李 强,安俊斌,陈 雷,马 超

(中北大学 机电工程学院，山西 太原 030051)

为了改善高射速转管炮自动机的动力学性能，基于正弦型加速度凸轮曲线设计理论，运用五次多项式替代正弦型加速度规律对曲线槽过渡段进行优化设计，并基于MATLAB软件计算出优化后的凸轮曲线槽理论方程。然后利用ADAMS建立6管转管炮自动机虚拟样机模型，模拟其在6 000 发/min的射频下的动力学性能。计算结果表明，滚轮与凸轮曲线槽间的接触力平均降低了1.15 kN,同时机芯组加速度平均降低了105 m/s2，转管炮自动机的动力学性能也得到显著改善。

机械设计；高射速；转管炮；凸轮曲线槽；多项式替代

转管炮的射速越高，其自动机的动力性能越差，一方面,机芯组加速度增幅变大而导致滚轮与曲线槽之间的碰撞力加大，从而使自动机的使用寿命缩减；另一方面，相应的驱动功耗也会大幅增加，自然对电机功率要求更高。要解决这个问题，可以从两方面着手：一是从电机着手，采用更高功率的电机；另一方面，就是通过结构优化来提高自动机的动力学性能，从而提高自动机寿命。而曲线槽作为转管炮自动机的核心部件，其结构设计的优劣直接影响着自动机的使用寿命的长短。文献[1]提供了一种凸轮曲线槽的一种简便建模方法，为凸轮曲线槽的研究具有一定参考价值。文献[2]为降低对外部能源的需求，通过取消斜直线段，增加过渡段曲线角度的方法降低了机芯组的驱动功率。而文献[3]在文献[2]的基础上提出了通过去掉后直线段的方法进一步降低了机心组的加速度和功耗。笔者则是通过对凸轮曲线槽过渡段理论进行优化设计来提高自动机的动力学性能。

1 新型凸轮曲线槽分析与设计

1.1 正弦型加速度凸轮曲线方程

图1为转管炮采用最常见的正弦型加速度凸轮曲线槽的展开图。当转管炮的行星体旋转时，机心上的滚轮通过与炮箱本体上的曲线槽配合实现机心前方闭锁击发、后方抛壳进弹的连续射击动作。其中图1中的θ1主要保证机心闭锁确实后击发和膛压降到安全值时再开锁，而θ2主要保证弹丸可靠的抛壳和进弹，θ3所代表的过渡段则是设计的主要阶段。因为供弹速度要尽可能快，而闭锁击发时机心组速度又要减慢，因此它们之间进行速度转化时应尽可能平缓。所以过渡段的设计至关重要。

正弦型加速度凸轮曲线的过渡段设计分为3段,首尾两端为正弦曲线,中间段为二次曲线。

其中首尾两段的正弦曲线的设计主要采用的是摆线定理，即滚轮转过2π角时，柱体转过了β角，如图2所示。

由图2可推出，机心组的加速度为

(1)

式中:C1为滚轮的周长;w为行星体转速;v为机心组的速度。

为了与下一段加速度为常值的水平线段平滑连接，当相角为β时，加速度应取为极大值，有

β=4θA

(2)

将式(2)代入式(1)中即可得出各段曲线的方程，再输入各参量的理论值，即可得到曲线槽过渡段的理论方程。其过渡段加速度变化如图3所示。由图3可看出加速度变化平稳连续，机芯组运动冲击较小。

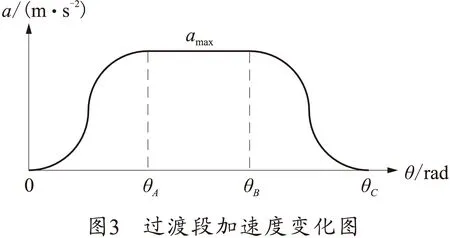
1.2 新型曲线槽的优化设计

由以上推导运动方程可以看出，凸轮曲线是圆柱体转角θ的函数。在机械原理中可知，从动件常用的运动规律有：等速运动、等加速等减速运动、简谐运动、正弦加速度运动、五次多项式运动规律和组合运动规律等。根据其运动特性分别适用于不同场合:等速运动适用于低速、轻载场合；等加速等减速运动适用于中速、轻载场合；简谐运动适用于中速、中载场合；正弦加速度运动主要应用于高速、中载的场合，其加速度变化平缓，因而将不产生冲击；五次多项式运动规律既无刚性冲击也无柔性冲击，其加速度曲线连续，理论上不存在冲击。

转管炮自动机在高速运转时，自动机各从动件运动速度都比较高，彼此之间的接触力也比较大，则只有正弦加速度运动和五次多项式运动规律适合于凸轮曲线槽设计。采用五次多项式设计过渡段时，只要多项式的幂次较高，总能满足运动始末两端的任意边界条件，还能使其与端点平滑连接。故笔者采用五次多项式运动规律对凸轮曲线过渡段进行优化设计。

与正弦型加速度过渡曲线设计有所区别的是，过渡段首尾两段采用五次曲线来代替正弦曲线，而中间段仍采用原来的二次曲线进行设计。选取凸轮曲线的前过渡段来进行改进，该过渡段一共分为3段，即首尾段和中间段，其位移、速度、加速度的假设方程分别为

(3)

式(3)中，x1，x2，x3分别代表过渡段首、中、尾3段的位移方程，同理其余方程是它们的速度和加速度方程。要求解这样的多项式运动方程，就需要相应的运动条件。因为是对过渡段曲线进行改进，那么首尾两段与中间段的过渡处位移、速度和加速度都是相等的，这样即得到了9个运动条件。又由θA,θB,θC处的边界条件，共得出12个运动条件。通过在MATLAB软件中用拟合法使机芯组的位移、速度、加速度平滑连接，求出3个假设运动条件为

(4)

然后解出方程组各个系数：

{C1,C2,C3,C4,C5,C6,C7,C8,C9,C10,C11,C12,C13,C14,C15}={0.005 1,-0.150 2,0.254 7,0,0,0,0.161 9,0.074 5,0.010 1,-0.109 3,-0.054 6,-0.056 0,0.161 9,0.194 1,0.059 7}

由以上系数即可求出过渡段的位移、速度和加速度方程。再输入相关参量的理论值即可求出凸轮曲线槽轮廓线，如图4所示。

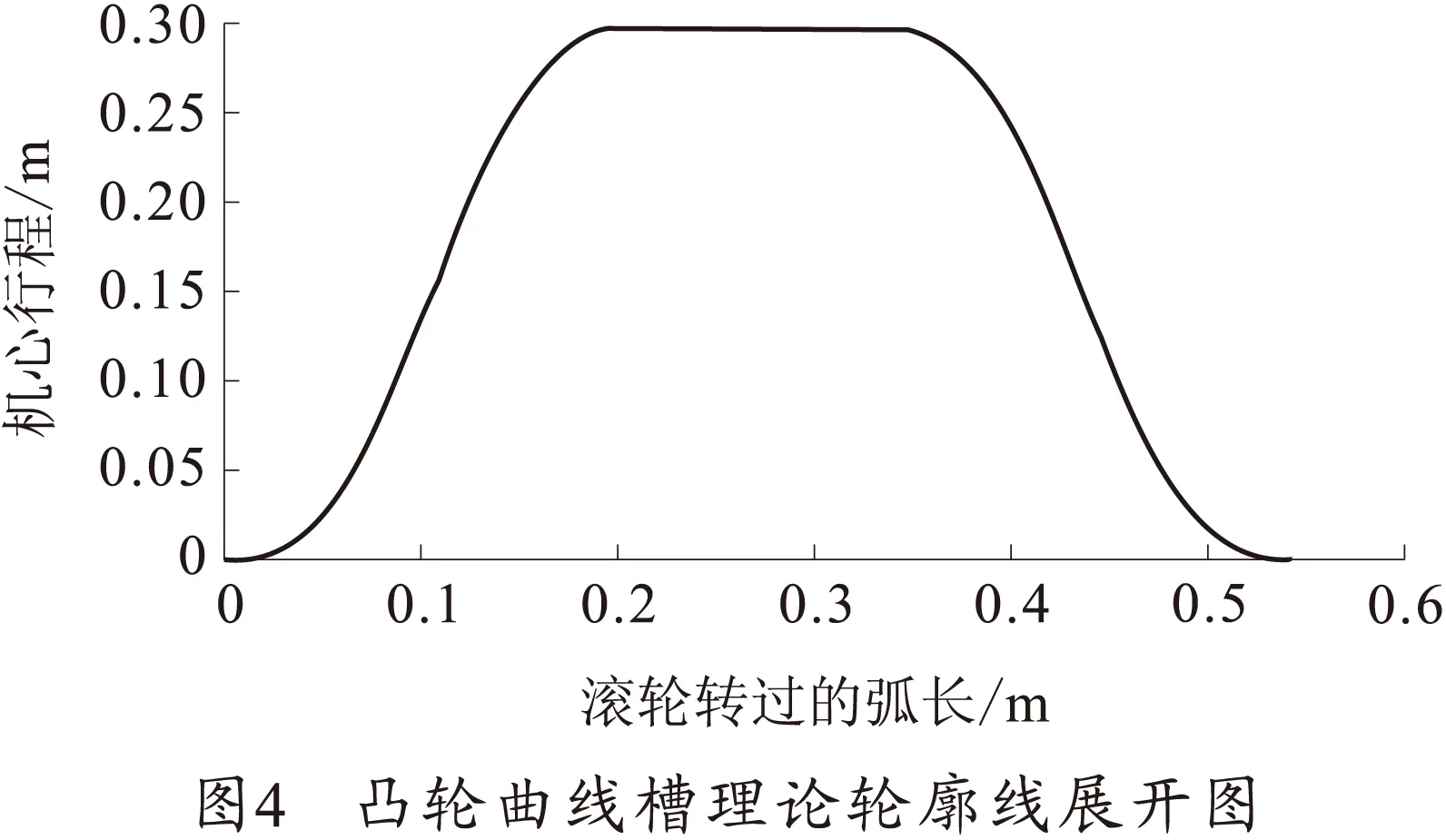
2 实例设计分析

笔者以6管6 000发/min高射速的转管炮武器为例进行分析。其自动机运动循环图如图5所示。其身管组转速为1 000 r/min，即6 (°)/ms。前直线段闭锁所需角度为10°，从击发到膛压降到安全允许值范围内，包括内弹道和后效期2个阶段。内弹道时期所用时间为3.57 ms，则内弹道时期所占角度为21.42°。内弹道结束时膛压为80.948 MPa，由后效期膛压公式P=80.948e-430t，计算膛压降到安全允许值时，其所用时间为3.25 ms，则后效期所占角度为19.5°。再加上考虑1—2 ms的迟发火时间及开锁所占角度17°，则前直线段所占角度取为74°。后直线段则抛壳和进弹所占角度，取为32°。其余是4个角度相等的过渡段，其角度均为63.5°。

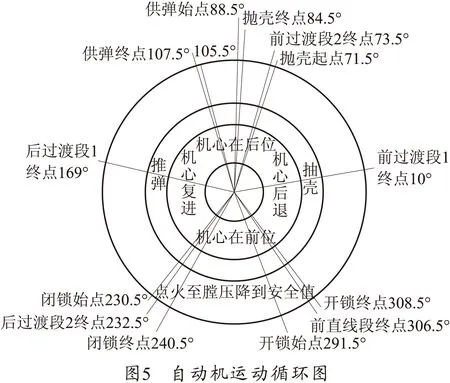
根据自动机运动循环图及前面推导出的曲线槽理论方程，运用MATLAB软件编程导出改进前后的凸轮曲线槽轮廓线数据点，然后用UG将数据点导入建立凸轮曲线槽的实体模型。然后分别以上述两种凸轮曲线槽建立自动机虚拟样机模型[4-5]，如图6所示。然后将自动机模型导入ADAMS软件中进行6管射速为6 000 发/min的动力学仿真，查看两种凸轮曲线槽的运动学及动力学特性如图7～10所示。

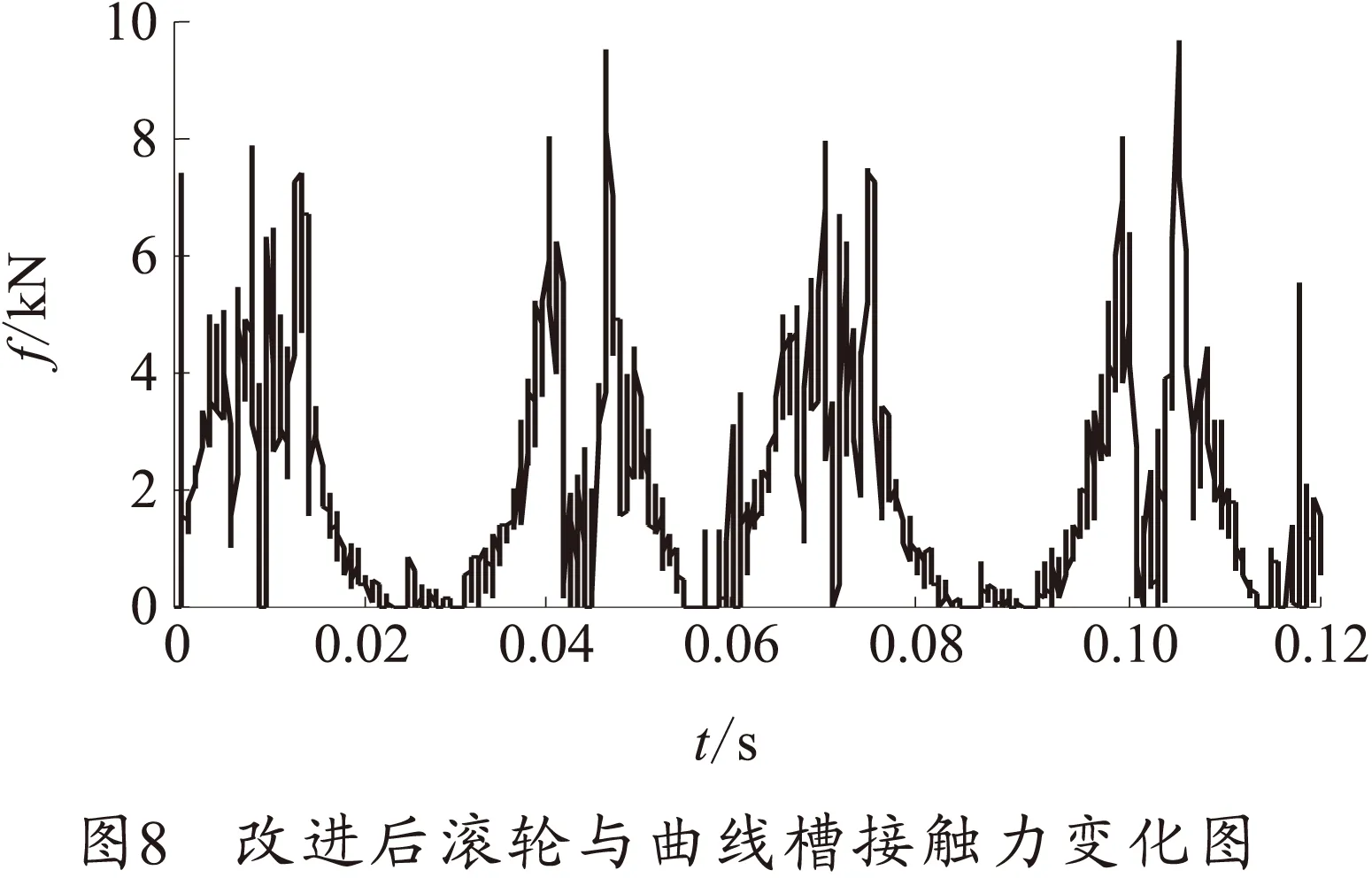
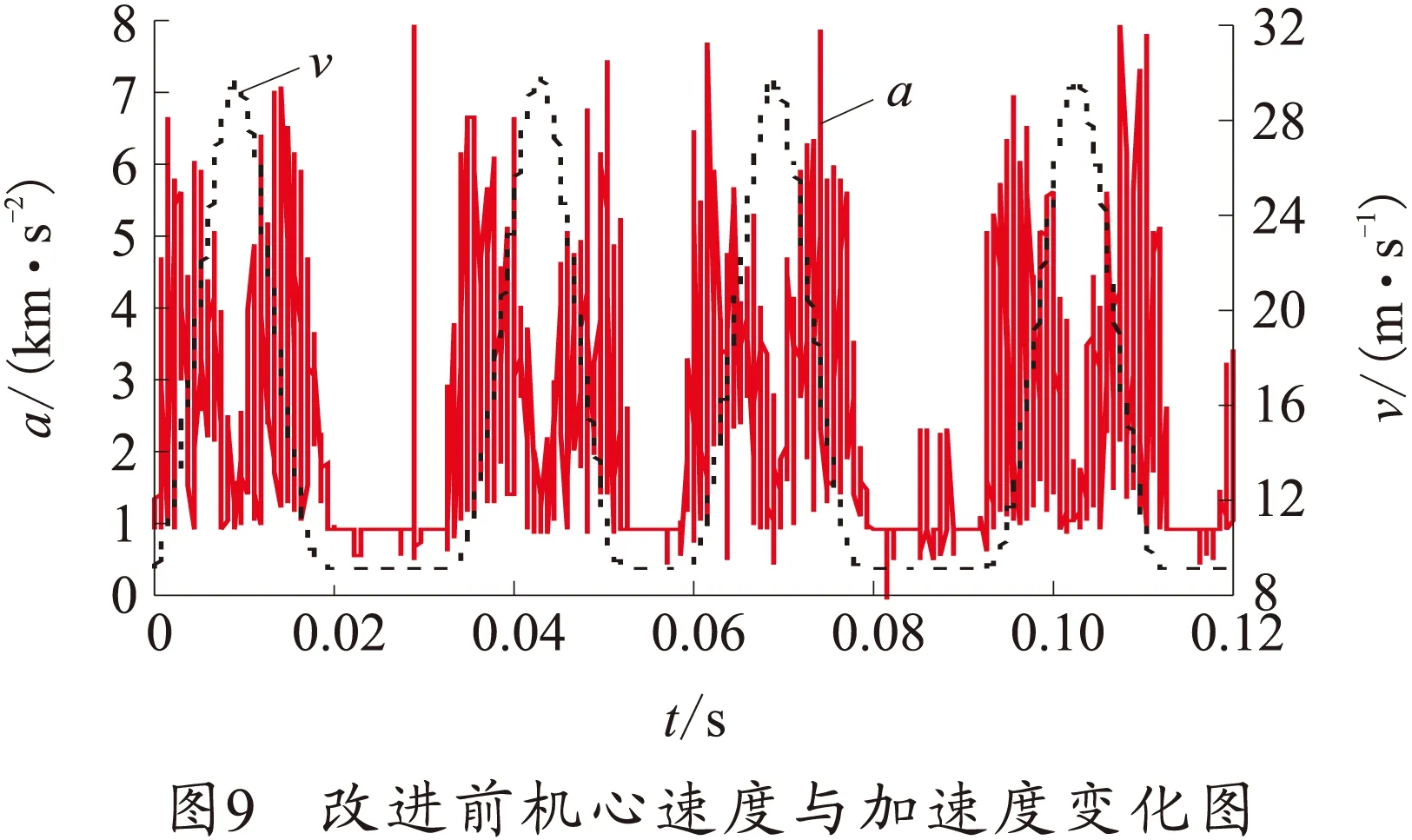
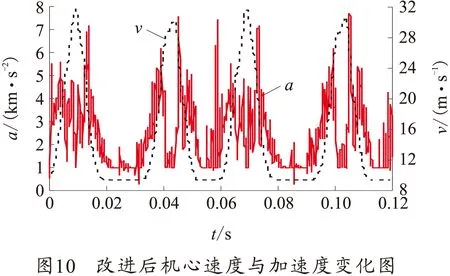
由图7、8可以看出，改进前滚轮与凸轮曲线槽的接触力最大值为14.472 kN，平均接触力为3.130 kN，而改进后滚轮与凸轮曲线槽的最大接触力为9.655 kN，平均接触力为1.980 kN，接触力平均降低了1.150 kN。可以看出采用新型凸轮曲线后滚轮与曲线槽的碰撞作用大大减小。同时，曲线槽与机心组的动力学性能有所改善。由图9、10可以看出，改进前机心组的运动加速度最大值为8 000 m/s2,平均加速度值约为2 572 m/s2，且加速度随速度变化时，其峰值振荡比较明显。而采用优化曲线后，机心组的最大加速度值仅有7 500 m/s2，平均加速度值约为2 467 m/s2，平均降低了105 m/s2在随速度变化过程中，其峰值振荡较弱，机心组的运动学性能有所改善。

3 结束语

在正弦型加速度凸轮曲线设计理论的基础上，提出一种用五次多项式代替正弦型加速度规律对曲线槽过渡段进行优化设计的方法。设计出的新型凸轮曲线槽能显著降低机心组的运动加速度，从而使自动机运转时各组件平稳可靠地按预定规律进行。采用新型凸轮曲线槽后，机心组滚轮与曲线槽之间的接触力大大减小，从而使机芯组与曲线槽之间的配合更加平稳，自动机的动力学性能也得到改善。

References)

[1]刘杰,李强.圆柱凸轮建模方法分析与研究[J].机械传动,2012(11):74-76. LIU Jie, LI Qiang.Analysis and reseatch of the cylindrical cam modeling method[J].Journal of Mechanical Transmission,2012(11):74-76.(in Chinese)

[2]郑建荣.ADAMS——虚拟样机技术入门与提高[M].北京：机械工业出版社，1990：171-176. ZHENG Jianrong.ADAMS：accidence and improvement of virtual protype technology[M].Beijing:China Machine Press,1990: 171-176.(in Chinese)

[3]郭卫东.虚拟样机技术与ADAMS应用实例教程[M].北京:北京航空航天大学出版社，2008：79-118. GUO Weidong.Virtual prototyping technology and ADAMS application examples tutorial[M].Beijing: Beihang University Press，2008: 79-118.(in Chinese)

[4]徐健,薄玉成,常学芳.超高射速转管炮凸轮曲线槽分析与改进[J].火炮发射与控制学报,2007(4):43-46. XU Jian, BO Yucheng, CHANG Xuefang. Analysis and improvement for cam curve groove for super-high fire ratio Gatling gun[J].Journal of Gun Launch & Control,2007(4):43-46. (in Chinese)

[5]徐健,薄玉成,常学芳.超高射速转管炮新型低功耗凸轮曲线设计[J].弹道学报,2009,21(2):70-73. XU Jian, BO Yucheng, CHANG Xuefang. New type of low power consumption cam curve designed for super-high fire ratio Gatling gun[J].Journal of Ballistics,2009,21(2):70-73. (in Chinese)

Optimization and Design of the Cam Curve Groove forHigh Fire Rate Gatling Gun

LI Shikang, LI Qiang, AN Junbin, CHEN Lei, MA Chao

(Mechanical and Electrical Engineering College, North University of China, Taiyuan 030051, Shanxi, China)

In order to improve the dynamic performance of the automaton for high fire rate Gatling gun, based on the design theory of sine acceleration cam curve, the optimal design of the transition section of curve groove is achieved by using the five degree polynomial instead of the rule of motion of sine acceleration. And based on the MATLAB software, the optimized theoretical equation of the cam curve groove is calculated. Then, the virtual prototype model of 6 tube Gatling gun is established through ADAMS with the dynamic properties of the model simulated in the radio frequency of 6 000 r/min. The calculation results show that the contact force between the rolling wheel and the cam curve groove is reduced by an average of 1.15 kN. Besides, the acceleration of bolt group is reduced by an average of 105 m/s2with the dynamic performance of the automaton in the Gatling gun improved greatly.

mechanical design; high fire rate; Gatling gun; cam curve groove; polynomial substitution

2016-05-09

国防科研基金项目资助(A0820132003)

李世康(1992—)，男，硕士研究生，主要从事高射速武器研究。E-mail：394127142@qq.com

10.19323/j.issn.1673-6524.2017.02.009

TJ391

A

1673-6524(2017)02-0040-04