基于坐标转换的炮兵观测器材倾斜修正模型
2017-06-19邱军钦
邱军钦
(南京炮兵学院 自行火炮系,江苏 南京 211100)
基于坐标转换的炮兵观测器材倾斜修正模型
邱军钦
(南京炮兵学院 自行火炮系,江苏 南京 211100)
针对传统炮兵观测器材调平过程中存在的诸多不足,提出一种基于三维直角坐标转换的可对炮兵观测器材因倾斜造成的测量误差进行修正的模型。根据方向盘结构和瞄准点法赋予基准射向的特点确定合适的角度测量参数,建立器材坐标系和大地坐标系,再进行坐标转换,得出倾斜修正模型。分别用MATLAB和Keil C51编写了倾斜修正程序,通过算例将程序计算结果和Solidworks模型测量结果进行比较,验证了模型的正确性和实用性。
炮兵观测器材;倾斜修正;坐标转换;调平
传统便携式或车载式炮兵观测器材在进行方位角、高低角测量之前,都需要一个调平的过程,即通过手动调节球轴或水平调整螺母,使水准器气泡居中[1]。在实战中,这一过程存在诸多不足:操作频繁、耗时,难以及时侦查;车载观测器材的调节范围有限,一般不超过6°[2],使侦察车的侦查能力受限;若操作不当或疏忽未能正确调平,将严重影响测量精度。
若使炮兵观测器材无需调平即可精确测量,就能节约测量的准备时间,有利于提高侦查的及时性、准确性和侦查分队的机动能力、生存能力。一种解决思路是对传统炮兵观测器材方向盘进行数字化改造,利用倾角传感器测出方向盘有关轴的倾角,辅以其他必要参数,让处理器根据方向盘在空间中的倾斜姿态对它的高低、方向转角进行修正,使修正结果与调平的方向盘测量结果一致。笔者根据这一思路提出一种基于三维直角坐标转换的炮兵观测器材倾斜修正模型。
1 方向盘测量原理
方向盘通过绕俯仰轴旋转的俯仰运动和绕方向轴旋转的方向运动二者的合成来完成视轴的移动。
使用方向盘之前,先进行调平,使俯仰轴位于水平面内,方向轴垂直于水平面。然后用瞄准点法为方向盘赋予基准射向,方法为:器材调平后,通过俯仰和方向运动使视轴瞄向瞄准点,再将器材方向分划装定为已知的瞄准点方向分划即可。
此时,以俯仰轴为x轴,以方向轴为z轴,以两轴交点为坐标原点O建立符合右手笛卡儿坐标系的器材坐标系O-xyz,点划线为视轴,它在O-yz平面内。若不进行调平,直接在方向盘倾斜状态下用瞄准点法赋予基准射向。视轴瞄向瞄准点时,以O为原点,以视轴在水平面的投影为Y轴,以水平面内过O点且与Y轴垂直的直线为X轴,以过O点且与水平面垂直的直线为Z轴,建立符合右手笛卡儿坐标系的大地坐标系O-XYZ。器材坐标系O-xyz和大地坐标系O-XYZ的相对位置关系如图1所示,图中视轴瞄向瞄准点。

设瞄准点方向分划为θ,视轴瞄向瞄准点并装定好瞄准点方向分划后,即可向目标瞄准并读取器材高低分划α和器材方向分划β,规定视轴从O-xy平面瞄向目标的高低转角为器材高低角a且以向上转为正,从O-yz平面瞄向目标的方向转角为器材方向角b且以俯视器材时顺时针旋转为正,则:
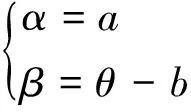
(1)
若方向盘已调平,即图1中器材坐标系O-xyz和大地坐标系O-XYZ重合,则读得的器材高低分划可作为观目高低分划φ的测量值,器材方向分划可作为观目方向分划ω的测量值,即:
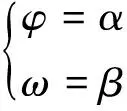
(2)
式(2)就是方向盘的测量原理。但若方向盘未调平,式(2)即不再适用。设此未调平状态下观目高低分划和观目方向分划与器材高低分划和器材方向分划之间的函数关系为
(3)
式(3)是炮兵观测器材倾斜修正模型。
2 方向盘倾斜姿态的描述
在方向盘未调平状态下使视轴瞄向瞄准点,如图1所示,设c为此时视轴与y轴的夹角;d为此时视轴与Y轴的夹角,即视轴的倾角(规定视轴指向水平面以上为正),可通过倾角传感器测出,范围为-1 500~1 500密位;e为俯仰轴与它在水平面的投影的夹角,即俯仰轴的倾角(规定x轴正方向指向水平面以上为正),可通过倾角传感器测出,范围为-1 500~1 500密位;f为x轴与X轴的夹角,规定其符号与e相同。方向盘在空间中的倾斜姿态可用c、d、e和f描述。
在大地坐标系O-XYZ中,用空间单位方向向量n1=(X1,Y1,Z1)表示瞄准点方向,n1在O-YZ平面内,且与Y轴夹角为d,则:
(4)
在大地坐标系O-XYZ中,用空间单位方向向量n2=(X2,Y2,Z2)(X2>0)表示器材坐标系O-xyz的x轴正方向,n2与O-XY平面的夹角为e,则:
Z2=sine
(5)
X22+Y22+Z22=1
(6)
因为n1⊥n2,所以n1·n2=0,即:
X1X2+Y1Y2+Z1Z2=0
(7)
将式(4)和式(5)代入式(7)得:
Y2=-sinetand
(8)
在大地坐标系O-XYZ中,用空间单位方向向量n3=(1,0,0)表示X轴正方向,n2与n3的夹角为f,则:
(9)
联立式(5)、(6)、(8)、(9)得:
(10)
3 炮兵观测器材倾斜修正模型
用空间单位方向向量n表示任意瞄向目标的视轴指向。在O-xyz中,令n=(x,y,z),则:

(11)
在O-XYZ中,令n=(X,Y,Z),规定n与其在O-XY平面的投影的夹角为观目高低角A(规定n指向O-XY平面以上为正),n在O-XY平面的投影与Y轴的夹角为观目方向角B(规定n在O-XY平面的投影相对Y轴正方向偏右为正),则:
(12)
观目高低分划φ、观目方向分划ω与观目高低角A、观目方向角B的关系为
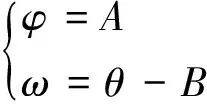
(13)
给出以上设定后,若读得视轴瞄向目标时的器材高低分划α和器材方向分划β,则由式(1)可求得器材高低角a和器材方向角b,再由式(11)可求得n在O-xyz中的坐标(x,y,z)。若能由(x,y,z)得到n在O-XYZ中的坐标(X,Y,Z),则由式(12)可求得观目高低角A和观目方向角B,再由式(13)可最终求得观目高低分划φ和观目方向分划ω。因此,问题可转化为:已知空间单位方向向量n在O-xyz中的坐标(x,y,z),求其在O-XYZ中的坐标(X,Y,Z)。
从图1可以看出,器材坐标系O-xyz绕x轴逆时针旋转c,再绕y轴逆时针旋转f,最后绕x轴顺时针旋转d,可得到大地坐标系O-XYZ。
根据三维直角坐标转换模型[3],有:
(14)
式中,Rxyz为由器材坐标系O-xyz到大地坐标系O-XYZ的复合旋转矩阵。
联立式(11)、(12)、(14)得:
(15)
再联立式(1)、(13)、(15),即可得到式(3)的完整表达式:
(16)
综上所述,c、d、e一旦确定,则器材坐标系与大地坐标系的相对位置关系唯一确定,再由式(10)求得f,即可由未调平状态下方向盘的器材高低分划α和器材方向分划β计算出观目高低分划φ和观目方向分划ω。
4 算例分析
为验证该模型的正确性,分别在MATLAB平台和Keil C51单片机集成开发环境下对式(15)编写了计算程序,并在Solidworks三维CAD软件中建立了大地坐标系和器材坐标系模型,然后给定4个典型位置条件,将程序计算结果和Solidworks模型测量结果(小数位数采用默认值)进行比较,结果如表1所示。其中A1、B1是Solidworks的模型测量结果,A2、B2是MATLAB的计算结果,A3、B3是Keil C51的计算结果。

表1 给定条件下的程序计算与模型测量结果 密位
从表1中可看出,程序计算结果与Solidworks模型测量结果一致。该模型建立在精确坐标转换[4]的基础上,并没有进行线性或非线性近似[5],因此可以说是对倾斜的无差修正。另外,程序在Keil C51(采用11.059 2 MHz晶振[6])中的模拟运算时间约为0.18 s,说明采用最基本的51单片机就能达到很高的计算效率,满足实战要求。
5 结束语
笔者基于三维直角坐标转换提出了炮兵观测器材倾斜修正模型。分别用MATLAB和Keil C51编写计算程序,并通过算例验证了模型的正确性和实用性。该模型可解决炮兵观测器材调平过程的不足,为传统炮兵观测器材的数字化改造省去测量前的调平过程提供了理论依据。
References)
[1]贺有. 炮兵侦查指挥[M]. 南京:南京炮兵学院出版社,2014:274-275. HE You. Command of the artillery reconnaissance[M]. Nanjing:Publishing House of Nanjing Artillery Academy,2014:274-275. (in Chinese)
[2]刘利民,尤新生. 炮兵分队战术(自行火炮)[M]. 南京:南京炮兵学院出版社,2014:44-45. LIU Limin,YOU Xinsheng. Tactics of artillery unit (SPG) [M]. Nanjing:Publishing House of Nanjing Artillery Academy,2014:44-45. (in Chinese)
[3]周维虎,兰一兵,丁叔丹,等. 空间坐标转换技术的分析与研究(一)[J]. 航空计测技术,1999,19(4):10- 12. ZHOU Weihu,LAN Yibing,DING Shudan,et al. Analysis and study on space coordinate transformation technology(1)[J]. Aviation Metrology & Measurement Technology,1999,19(4):10-12. (in Chinese)
[4]张宏. 布尔莎-沃尔夫转换模型的几何证明[J]. 测绘与空间地理信息,2006,29(2):46-51. ZHANG Hong. To prove Burse-Wolf conversion model with simple formula [J]. Geomatics & Spatial Information Technology,2006,29(2):46-51. (in Chinese)
[5]曾文宪,陶本藻. 三维坐标转换的非线性模型[J]. 武汉大学学报:信息科学版,2003,28(5):566-568. ZENG Wenxian,TAO Benzao. Non-linear adjustment mo-del of three-dimensional coordinate transformation[J].Geomatics and Information Science of Wuhan University,2003,28(5):566-568. (in Chinese)
[6]郭天祥. 新概念51单片机C语言教程:入门、提高、开发、拓展全攻略[M]. 北京:电子工业出版社,2009:132- 133. GUO Tianxiang. New concept 51 MCU C language tuto-rial:full strategy of introduction,improvement,development and expansion[M]. Beijing:Publishing House of Electronics Industry,2009:132-133. (in Chinese)
Tilt Correction Model of Artillery Observation EquipmentBased on Coordinate Conversion
QIU Junqin
(Department of Self-propelled Guns,Nanjing Institute of Artillery,Nanjing 211100,Jiangsu,China)
In view of the leveling deficiency in using the traditional artillery observation equipment, a model is put forward based on the three-dimensional rectangular coordinate conversion to correct the tilt. Measuring parameters are determined according to the features of the magnetic compass director’s structure and aiming point method of giving reference direction. Then equipment coordinate system and earth coordinate system are established. Finally, the tilt correction model is built using coordinate converse. Tilt correction program is written with MATLAB and Keil C51. The calculated results of the program coincide with the measurement results of the mechanical model established in Solidworks through comparison, which proves the correctness and practicability of the model.
artillery observation equipment; tilt correction; coordinate conversion; leveling
2016-03-19
邱军钦(1992—),男,学士,主要从事炮兵指挥技术研究。E-mail:1260188801@qq.com
10.19323/j.issn.1673- 6524.2017.02.003
E933
A
1673-6524(2017)02-0011-04
