某AU型螺旋桨的三维建模及其性能分析

安 邦,朱汉华,范世东,张喜胜,黄 鑫

(武汉理工大学 能源与动力工程学院，湖北 武汉 430063)

某AU型螺旋桨的三维建模及其性能分析

安 邦,朱汉华,范世东,张喜胜,黄 鑫

(武汉理工大学 能源与动力工程学院，湖北 武汉 430063)

螺旋桨性能将直接影响船舶的快速性和推进效率，文章以AU型螺旋桨为对象，运用实体建模和数值仿真等方法对螺旋桨性能进行研究。首先用MATLAB将螺旋桨的基本参数和不同半径处叶切面二维坐标转换为空间笛卡尔坐标，再将笛卡尔坐标值导入Solidworks中建立三维实体模型，然后在Fluent中选择RNGk-ε湍流模型，运用CFD数值方法对螺旋桨进行性能仿真，研究不同进速下螺旋桨的推力系数、转矩系数、敞水效率和桨叶压力分布等参数特性变化趋势，分析计算结果的准确性。通过对螺旋桨性能的分析，得到螺旋桨运转时尾流场特性，为空泡、振动分析提供理论依据，为以后螺旋桨优化设计提供参考。

螺旋桨；三维建模；性能分析

自西江水系打造亿吨级黄金水道以来，船舶数量和货物总量迅猛增长。螺旋桨作为船舶上的推进器，其性能的优劣是决定船舶能否达到航行要求的关键因素[1]，但是现有西江干线船舶的螺旋桨特性并不能满足航行需求，因此有必要开展船舶螺旋桨性能研究。螺旋桨桨叶是自由曲面并且是螺旋面的一部分，因其形状复杂无法用函数形式准确的表达该类曲面，只能通过桨叶的叶切面型值，采用曲线拟合法，并经过复杂的投影换算关系才能获得螺旋桨叶面的拟合曲面[2]。目前大多数科研人员用实验的方法来得到螺旋桨在敞水下的水动力性能，实验方法得到的结果虽然准确度较高，但是费时、费力、成本较高。现在螺旋桨设计理论是势流理论，如升力线方法和面元法等，对于预报螺旋桨的水动力特性分析计算难度较高，但是随着科技的进步尤其是计算机技术的发展，采用计算流体力学(CFD)方法来获得螺旋桨水动力性能结果已经成为可能，能在保证计算结果精度的前提下大大缩短计算周期[3]。目前，如何提高 CFD 方法对螺旋桨黏性流场的预报精度已成为国际上的一个研究热点。一般而言，影响 CFD方法对螺旋桨黏性流场预报精度的因素主要有两个，一是流场建模及网格化分，二是湍流模型的选取。许多研究者对现有湍流模式的适用性做了大量的研究，并对某些湍流模型进行了适当的改进。但是，目前还没有一种湍流模式可以适用于任何类型的问题，湍流模式的选取主要应考虑流场的流动特点、所需的精度要求和计算机硬件条件等[4]。根据螺旋桨几何形状和流场特性，采用一种适合螺旋桨敞水性能计算的分区混合网格划分方案，结合不同湍流模型对螺旋桨敞水性能进行了数值仿真，对精度较高的RNGk-ε湍流模型的计算结果进行了分析。

以AU4-40型螺旋桨为研究对象，基于MATLAB编程语言，利用螺旋桨参数、桨叶不同半径处切面二维型值点坐标得到桨叶切面的三维空间笛卡尔坐标[1]，将得到的三维坐标导入到Solidworks中进行三维建模。最后采用CFD软件Fluent对螺旋桨的水动力性能进行仿真计算并分析结果。

1 螺旋桨三维建模

根据螺旋桨基本参数和桨叶不同半径处切面二维形状尺寸，建立螺旋桨曲面所有型值点空间坐标的关系式如下：

(1)

式中：X、Y、Z为型值点的三维坐标；Ri为不同截面处半径；Y1为距母线的距离；Z1为叶背、叶面的切面纵坐标；φ为螺距角；θ为后倾角。

某AU型螺旋桨的基本参数如表1所示。

表1 螺旋桨的基本参数

运用参数与式(1)，计算0.2R～0.95R(R为螺旋桨半径)半径处切面的空间笛卡尔坐标，并保存为.txt文件，导入到Solidworks中，在软件中生成的空间点连接成光滑的曲线，通过填充命令生成多个切面，如图1(a)所示；通过放样命令并以导边、随边为导引线将多个叶切面连成光滑桨叶实体，如图1(b)所示；最后执行阵列命令生成4叶桨，并对叶稍部分进行优化处理，在叶根部分进行倒角处理，最终模型如图1(c)所示。

图1 螺旋桨三维模型生成

2 螺旋桨性能仿真

2.1 螺旋桨流场仿真模型网格划分及边界条件设定

利用Hypermesh建立流场模型，把流体分为内部旋转区域和外部静止区域，外部静止区域为直径5D(D为螺旋桨直径)、长度10D的圆柱体，靠近叶背的面设为进口，另一端设为出口；内部旋转区域为直径1.2D、长度0.8D[5]，2个区域中心轴均为桨模型的Z轴。对旋转域使用非结构化的网格，对于流场进口处和出口处因其流域变化缓慢，所以网格适当稀疏；旋转域网格约为67万个。外部静止流场较内部旋转流场网格密度低，在保证计算精度的前提下尽可能的加快计算时间。静止域部分约有20万网格，两部分共约87万网格，如图2。

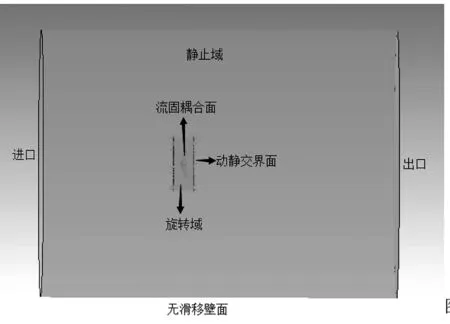
图2 螺旋桨流场仿真模型示意图

由图2知，流场进口设为速度进口，出口设为自由出口，静止域外部边界设为无滑移壁面，旋转域外表面和静止域内表面其实是一个面，在Fluent中要将这2个面进行连接操作，形成2个流场区域数据传递面。将螺旋桨实体抑制后，原来的螺旋桨表面成为旋转域的内表面，在Fluent中将该面设为流固耦合面[5]，由于还存在内边界，但不影响分析结果，因此对这些面不做特殊的设定。

2.2 湍流模型的选取

仿真模型分别选取Realizablek-ε湍流模型、RNGk-ε湍流模型以及标准k-ε湍流模型3种湍流模型进行螺旋桨水动力仿真试算，根据航行船舶的运行参数设定螺旋桨转速为324 r/min，螺旋桨进速依次取10～20 km/h之间11组数据，试算水动力性能结果，如表2所示。

表2 螺旋桨在3种湍流模型下仿真结果

由表2可以看出,在3种模型试算中，Realizablek-ε湍流模型计算结果跨度较大，与理论值的变化趋势不一致；标准k-ε模型得到的计算值小于其它2种模型，所以文中选择RNGk-ε湍流模型较为合理。

2.3 不同进速情况下螺旋桨特性对比分析

先用上海交通大学的AU系列螺旋桨敞水性能回归经验公式(2)、(3)分别计算推力系数Kt、转矩系数Kq，然后以RNGk-ε湍流模型作为初始场计算螺旋桨的敞水性能，设定螺旋桨转速n为324 r/min，船舶速度在10～20 km/h间，根据公式(5)～(7)分别得到推力系数Kt、转矩系数Kq和敞水效率η。计算结果如表3所示，对比结果如图3所示。

(2)

(3)

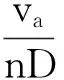
(4)

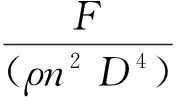
(5)

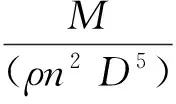
(6)

(7)

式中：Aijk、Bijk分别为推力系数和转矩系数的回归系数；J为进速系数；va为进速，m/s；ρ为水的密度，kg/m3；F为推力，kN；Ρ为转矩，kN·m；D为螺旋桨直径,m；n为螺旋桨转速,r/s；M为力矩,kN·m；Ae/Ao为盘面比;P/D为螺距比。

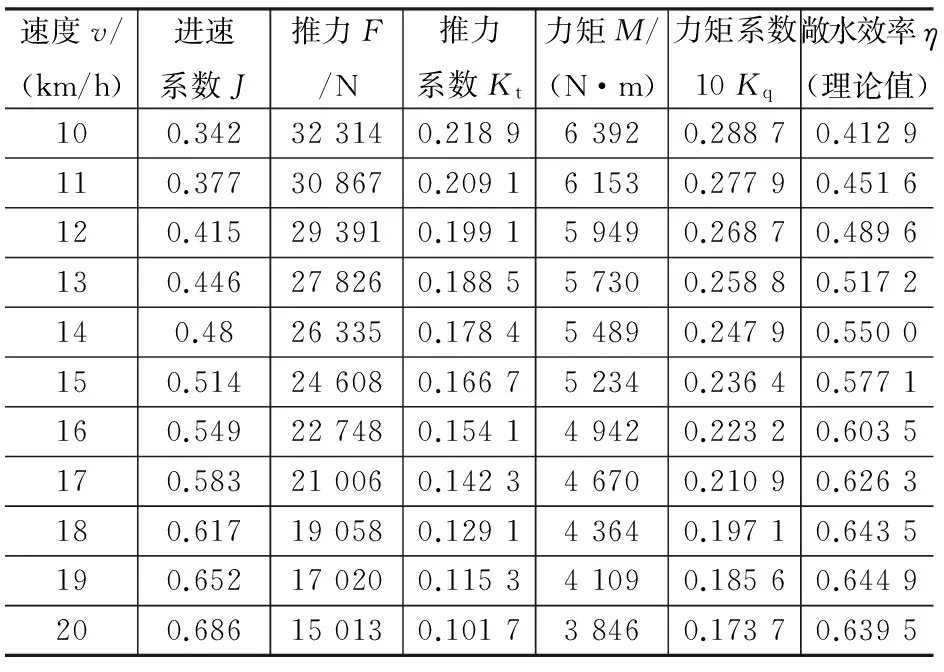
表3 螺旋桨水动力计算数值表

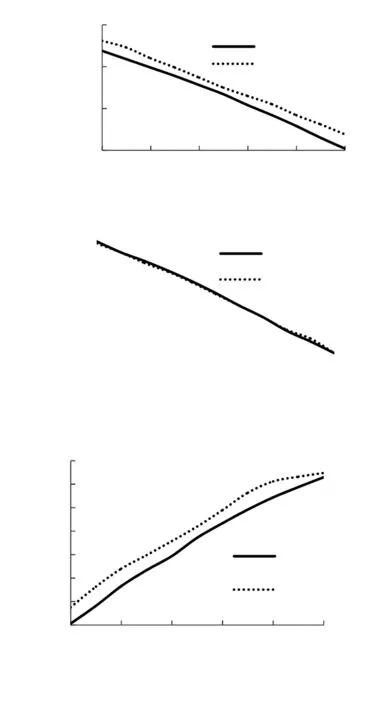
图3 螺旋桨特性对比图

通过图3可得：在不同进速情况下， Fluent 计算的仿真结果和理论值变化趋势基本一致，仿真计算的推力系数均小于理论值，当速度为14 km/h 时，两者误差最小约为4% ，当速度大于14 km/h后，随着速度增加两者间误差有增大的趋势。当速度小于18 km/h 时，推力系数的误差保持在8%以内，能满足实验要求。由变化趋势可以预见，本模型不适用于螺旋桨速度超过20 km/h的运动工况。

在不同进速的情况下，力矩系数仿真结果值和理论结果非常接近，而且变化趋势也基本一致，在螺旋桨进速为18 km/h以下时，误差在1%以内；速度为20 km/h时，两者数值差异相对较大,但也符合实验要求。所以在Fluent中得到的力矩系数仿真结果合理适用。

在不同进速情况下，螺旋桨敞水效率仿真值小于理论计算结果，并且变化趋势与推力系数误差情况基本一致，这也从侧面验证了螺旋桨效率仿真计算和理论计算过程误差可以忽略不计。但当速度超过18 km/h时，敞水效率理论与仿真结果差别较大，随着速度逐渐增加，敞水效率增长越来越缓慢，有变为水平的趋势，可以预见，螺旋桨在速度为20 km/h左右时敞水效率达到最大，然后逐渐下降。所以仿真结果可以作为螺旋桨速度在20 km/h以下时水动力性能对比研究的依据。

2.4 桨叶表面压力分布情况分析

在不考虑船体干扰的情况下，保持船速为12 km/h。转速为324 r/min，得到螺旋桨的压力云图。

螺旋桨面部的压强范围为0～0.123 MPa，桨叶面部压力大于桨叶背压，桨叶根部分压力为负值，桨叶面整体压力为正，桨叶面压力变化趋势较为规律，叶面压力分布由导边向随边逐渐减小，在r=0.5R处导边边缘出现压力最高值，导边压力最大达到0.123 MPa，叶面压力方向与螺旋桨产生推力方向一致。

螺旋桨背部的压强范围为-0.113 2～0.049 0 MPa，桨叶背压变化趋势较为规律，叶背压力分布由导边向随边逐渐增加，并且压力值从叶根到叶稍逐渐减小，在r=0.8R周围的叶稍区域出现最低压力值，随边压力为正值，导边压力值为-0.1132 MPa,叶背压力方向与螺旋桨产生推力方向相反。

一般认为，淡水在20 ℃时的饱和蒸汽压力约为0.003 MPa，在此温度下运行的螺旋桨，如果表面某处的压力低于此饱和蒸汽压力就会出现空泡现象，叶背压力较低，很容易发生空泡现象，当推力很小或为负值时，叶面区域也可能发生空泡现象。

在进速系数相同的情况下，叶面的表面压力要大于叶背的表面压力，这也符合螺旋桨的实际运行工况，叶面、叶背间的压力差与阻力的代数和就是螺旋桨的推力。

2.5 螺旋桨尾流情况分析

在不考虑船体干扰的情况下，保持船速为12 km/h，转速为324 r/min，得到螺旋桨尾流场流线图，如图4所示。

图4 尾流场流线图

从图4可以看到，水流经螺旋桨后的速度与方向的变化，随着与桨叶的远离，外流场的变化与影响迅速减小，恢复到原来状态，流动情况符合螺旋桨运转时的实际流动。

依次取进速系数为0.500、0.833、1.100时，得到螺旋桨表面的流线形状及其在随边处汇合形成的泄出涡形状图，如图5所示。从图5可以看到，随着进速系数的增大，螺旋桨尾流螺距也随之增大，同时可以看到螺旋桨尾流的外直径小于螺旋桨的直径。随着进速系数的增大，尾流的外直径也随之增大，采用PIV测量侧斜桨尾流，也显示了相同的情况。在J=0.500时，螺旋桨的直径明显大于尾流的外直径反映了重载荷时螺旋桨对流体有较强的抽吸作用[6]。

图5 螺旋桨尾流图

3 结束语

通过仿真分析，得到如下结论。

1)根据坐标转换关系，利用MATLAB程序将螺旋桨基本参数和不同切面处二维坐标转换为空间笛卡尔坐标，将空间笛卡尔坐标直接导入到Solidworks中进行螺旋桨的三维建模及叶稍优化处理，能够让大量数据快速的转化为直观的实体模型，使得整个螺旋桨建模过程快捷、高效，精确度较高。

2)采用CFD技术仿真AU型螺旋桨的性能，选择RNGk-ε湍流模型，得到不同进速系数情况下螺旋桨的性能参数，与理论值相比，仿真值误差小，计算精度满足要求，因此可以可靠的仿真螺旋桨的性能。

3)分析螺旋桨桨叶压力分布情况，可以清晰观察到桨叶上压力分布情况，能对流动有直观的了解。 同时也可以观察到螺旋桨尾流场随进速系数的变化而产生的变化情况。定性和定量上预报螺旋桨的流场特征为空泡、振动的分析提供理论依据，为螺旋桨的优化设计提供参考。

[1]吴利红, 董连斌, 许文海. 基于MATLAB和ProE的螺旋桨三维建模[J]. 大连海事大学学报, 2011(2):17-20.

[2]薛侠峰, 严天宏, 何波. MAU型螺旋桨建模与水动力性能分析[J]. 船舶工程, 2016(1):38-42.

[3]Hayati A N,Hashemi S M,Shams M.A study on the behind-hull performance of marine propellers astern autonomous underwater vehicles at diverse angles of attack[J].Ocean Engineering,2013,59(1):152-163.

[4]姚震球, 高慧, 杨春蕾. 螺旋桨三维建模与水动力数值分析[J]. 船舶工程, 2008, 30(6):23-26.

[5]余卫, 朱汉华, 黄灵勇,等. 西江干线船用螺旋桨性能分析与对比研究[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(1):198-202.

[6] Felice F D, Florio D D, Felli M, et al. Experimental Investigation of the Propeller Wake at Different Loading Conditions by Particle Image Velocimetry[J]. Journal of Ship Research, 2004, 48(2):168-190.

少些尘土 再现碧蓝天空

In this paper,the performance of propeller is studied by using the method of solid modeling and numerical simulation ,which is based on the AU type propeller.The basic parameters of the propeller blade section and different radius two-dimensional coordinates are converted the space Descartes coordinate with MATLAB.Descartes coordinates model is to establish 3D entity into Solidworks and the RNGk-εturbulence model is selected in Fluent,the performance of propeller being simulated with CFD numerical method,with which accuracy of analysis results can be achieved by studying change of thrust coefficient,propeller torque coefficient,open water efficiency and blade pressure distribution characteristics of different trends.Through analysis of the propeller performance,wake field characteristics is got at its operation,which provides a theoretical basis for analysis of cavitation and vibration and technical support for optimization design of propeller.

propeller;3D modeling;performance analysis

安邦(1991-)，男，山东日照人，在读硕士研究生，研究方向为船舶螺旋桨水动力性能。

U672

10.13352/j.issn.1001-8328.2017.03.016

2016-12-07