直线与圆中一道数量积为定值问题的探究
2017-06-13筅湖北省黄石有色第一中学余明
筅湖北省黄石有色第一中学余明
直线与圆中一道数量积为定值问题的探究
筅湖北省黄石有色第一中学余明
例1如图1所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线与圆A相交于M,N两点,Q是弦MN的中点,直线l与l1相交于点P.
(1)求圆A的方程.
解析:(1)圆A:(x+1)2+(y-2)2=20.(过程略)
(2)①当直线l与x轴垂直时,易知x=-2,符合题意.
②当直线l与x轴不垂直时,设直线l的方程为y= k(x+2).

图1
当直线l与x轴不垂直时,y=k(x+2),且(x+1)2+(y-2)2= 20,则因为|MN|=2,所以|AQ|=1.
故直线l的方程为3x-4y+6=0.
综上,所求直线l的方程为x=-2或3x-4y+6=0.
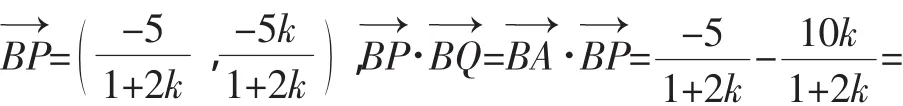
例2已知圆C:x2+(y-3)2=4,一动直线l过A(-1,0)与圆C相交于P,Q两点,M是PQ的中点,l与直线m:x+3y+ 6=0相交于点N.
解析:(1)①当直线l与x轴垂直时,易知x=-1符合题意.
②当直线l与x轴不垂直时,设直线l的方程为y=k(x+ 1).
故直线l的方程为4x-3y+4=0.
综上,所求直线l的方程为x=-1或4x-3y+4=0.
②当直线l与x轴不垂直时,设直线l的方程为y=k(x+ 1),由
例3圆C:(x-a)2+(y-b)2=r2,过定点A(x0,y0)的直线l与圆C交于P,Q两点,M是PQ的中点,l与直线m:y=kx+m相交于N,探索k为何值时为定值与直线l的斜率无关.

图2

(1)若x0≠a,y0≠b,因为AC⊥m,所以
(2)若x0=a,或y0=b,亦可得到为定值,不再赘述.
例1的第(3)问也可以这样解答:kAB=2,直线l1的斜率,所以满足l⊥AB.1
又x0=-2,y0=0,a=-1,b=2
此方法是运用数量积的定义,转化成投影来计算,从而得出数量积为定值的条件是AC⊥m,与直线l的斜率无关.这也是向量问题的妙解,除了常规的解析法通过大量的计算来解答,结合向量的加减运算和数量积的定义的运用能够事半功倍!在此不仅求出定值,而且弄清楚为什么会是定值,最终转化成求点到直线的距离和两点间的距离的积或积的相反数.F
