一堂常态课教学的“忠”与“创”
——以必修4“二倍角三角函数(2)”为例
2017-06-13俞培庆,王华民,王国星
·江苏省无锡市王华民名师工作室·
一堂常态课教学的“忠”与“创”
——以必修4“二倍角三角函数(2)”为例
筅江苏省太湖高级中学俞培庆
筅江苏省无锡市滨湖区教研中心王华民
筅江苏省太湖高级中学王国星
【问题提出】
近年来,我们听了很多课,感觉到在“用教材教”方面有下列倾向:一是过于依赖教材,表现在上课的内容,包括例题、练习均按教材的顺序呈现,几乎没有什么改变;二是甩开教材,另行一套.当然,大部分教师是介于两者之间,对教材有一点改动.不少教师有一些困惑:改什么?如何改?这是本文要研究的重要内容.
数学教材是依据课程标准,经专家不断打磨而成的书籍,是数学教学最重要的依据,因此教学需要忠于教材、尊重教材.但数学教学若只是照本宣科,那么,一方面无法体现教师的教学个性与创造性,另一方面,学生觉得只需要看书即可.久而久之,对一批优秀生缺乏吸引力,也难以体现教师的指导作用.因此,我们提出“既要忠于教材,又要对教材有所创造”的原则(以下简称“忠”与“创”).这里的“忠”是指遵循教材的编写意图、思想精髓、精神实质、整体结构和基本素材;这里的“创”是指不能照搬,要有所创造,能顺应学生的认知规律,呈现知识的发生、发展过程,注入教师的个性元素,重视和充分发挥教师的教学个性与创造.
【教材呈现】
苏教版必修4课题“二倍角三角函数(2)”的内容呈现如下:
首先教材106页提出一道思考题:在一个圆的所有矩形中,怎样的矩形面积最大?(见图1)
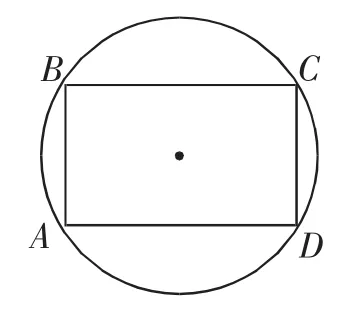
图1
(然后是如下的三道例题,解答从略):

图2
例3在半圆弧型钢板上截取一块矩形材料,怎样截取能使这个矩形的面积最大?(见图2)
【教学简案】
在王华民名师工作室的一
次研究课上,按照进度,执教的课题为“二倍角的三角函数(2)”.工作室两位青年教师自行备课,进行同课异构.
方案一
(一)问题情境
考考你:在半径为R的圆形钢板上截取一块矩形材料,怎样截取使得矩形面积最大?
温习公式:sin2α=__________;cos2α=_________= ________=__________;tan2α=__________.
降幂公式:cos2α=__________;sin2α=__________.
(二)深化理解
例4化简或求值.
解题收获:
例5求函数y=sin2x+sinxcosx-1的值域和单调递增区间.
(三)拓展探究
如图3,扇形AOB的半径为1,中心角为60°,四边形PQRS是扇形内接矩形,问:P在怎样的位置时,矩形PQRS的面积最大?并求这个最大值.
(四)课堂小结
方案二
(一)基础回顾
求值:(1)sin15°sin75°=________;
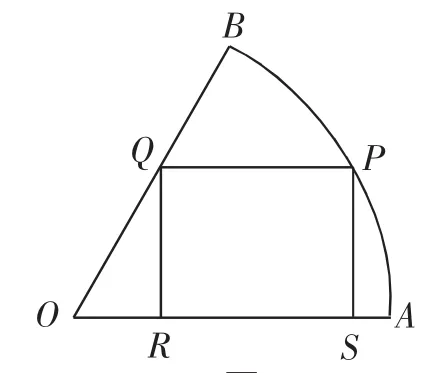
图3
(二)典例分析
按教材中的例1,例2,例3.其中,例1前补充教材中的思考题.
(三)练习(同方案一的拓展探究)
(四)课后小结
【反馈、感悟】
透过这堂课,结合笔者多年的教学实践,谈一些对“用教材教”的认识,以下侧重于新授课教学,谈如何找准“忠”与“创”的平衡点.
1.整体框架设计——找准“忠”与“创”平衡点
从整体架构上看,方案一对教材有所改编,从思考题入手,把思考题作为第一道问题解决(应用题),再进行变式,即教材的例3;例4的两小题涵盖了教材的例1、例2,改例2的证明为求值,又增加了一道例5,这道题与近年各地的高考题类似,通过降幂公式求函数的值域和单调递增区间.可见,方案一对教材有所创造,它增加了课堂的知识容量和思维容量,对学生思维训练有利.课堂反馈如下:第一道思考题,学生不会解答,费时较多,例5刚结束下课铃就响了,然后匆匆小结,拓展探究只能留课后.教学设计如何改进?因时间超出了,只能做“减法”.其一,减少例5,虽然例5是运用降幂公式,连接高考,比较重要,但考虑时间因素,放在单元复习课比较合适.其二,费时多主要表现:(1)例1用展开和降次两种方法求解,适度的一题多解,是培养发散思维的需要,不能减少;(2)对思考题的处理用时过多,需要作调整.可见,对教材的再创造有一定的风险.
方案二尊重教材,忠于教材,大部分保留教材内容,只有在开始增加了逆向思考的练习,把思考题放在例3前,增加了一道探究练习.课堂反馈如下:课堂推进比较顺利,但教师的个性和创造性没能体现,对学生的思维训练略显不足.
教材的编写方式通常是直接给予式,“冰冷知识”的直接呈现,隐去了知识形成的艰辛和知识发展的“火热思考”,课程改革倡导探究式学习,因此我们进行整体设计时,要提供素材让学生经历探索过程,用“火热的思考”积累数学基本活动经验,学会学习数学,这是一个学生主动“攫取”的过程,也就是“教人以渔”.这样,教师创造性地将教材改编为学生追求、探索、发现、争鸣、建构、总结、应用的科学有序的完善程序,做到变教材的“授”为学生的“取”,[1]重构框架,整合出彩.
2.创设问题情境——找准“忠”与“创”平衡点
方案一的课堂反馈:教师问了第一个学生,回答:连接AC,BD,在说几个角之间的关系.教师觉得方向不明,提示学生学以致用,可以设一个角来解决,然后问了第二个学生,回答“不会”.第三个同学站起来说,连接AC,过点O,教师追问其理由,学生回答:圆周角所对的弦是直径.可以设∠BCA=α,则BA=2Rsinα,BC=2Rcosα,矩形ABCD的面积S=BA·BC=4R2sinαcosα=2R2sin2α,最大值为2R2.当且仅当sinα=cosα,α=45°,此时截取的矩形为正方形,面积取得最大值.
变式反馈:不少学生能想到,连接OB,设∠BOA=α,则BA=Rsinα,BC=2Rcosα,矩形ABCD的面积S=R2sin2α.情境及变式大约11分钟.
“考考你”的情境,是课本上的一道思考题,学生是四星级重点高中的一个层次较高的班级,为何还出现这般冷场?利用三角工具解决一些实际问题,既是高考考查的重点内容,也是培养学生分析、解决问题能力的训练素材,更是培养学生核心素养“数学建模”的需要.但是通过设角建模,高一学生还是初次接触,许多同学想不到是很正常的,不足为奇.而经过教师富有耐心地循循善诱,才化解此冷场局面.后来的变式,学生已经有刚才的“设角”经验,能顺利解决.
其实,本课设置这个问题情境,其必要性值得商榷.设置该情境,从实际问题引出,有助于学生对二倍角重要性的理解,有利于学生数学兴趣的激发.然而,一节课的初始,问题情境偏难,费时偏多,数学探索的成本偏大了.另外,这节课是二倍角公式学习后的一节数学应用,作为学习的情境价值不大.
如何改进?可以进行如下两种处理.处理一:这个情境如果能放在二倍角的三角函数(1)开始呈现,让学生产生愤悱状态,到本节课解决,可能比较合适.处理二:尊重教材,按教材的顺序,先提出思考题“考考你”,思而不解,略作思考后,处理例1、例2、例3,解答后返回解决思考题,这样问题从易到难的设置,让学生拾级而上,学生有解决例3的经验,解决此思考题也不困难.教师需要再强化三角应用题的“贵在一设”(设角),不但节省时间,学生也得到了更多的思维训练,还使得学生增强了解决问题的信心.在议课时,也有老师认为干脆把思考题与例3的顺序对调,解决更顺畅.笔者觉得这是不妥的,因为圆内接矩形的情境比半圆内接矩形更符合实际,情境的自然性决定了先出现圆内接矩形,比较合理.

图4
创设情境的根本目的是为了引发学生思考,建构数学,无论是设置生活情境,提出问题,还是立足数学内部提出问题.如何创设情境主要取决于所教内容.如平面向量的基本定理,一位智慧教师创设下列生活情境,[2]投影图片(如图4)并解说:当前朝韩局势十分紧张,犹如箭在弦上,这枚攻击性的火箭炮在升空的某一时刻,速度可以分解为竖直向上和水平向前的两个分速度.提出问题:设该火箭炮发射某一刻的速度为v,其水平、竖直分速度分别为vx、vy,你能用vx、vy的式子表达v吗?创设该直观情境,有益于学生激发兴趣,全神贯注投入思考.有的内容难在抽象,可以创设直观情境,如让学生动手画图、实验等,在亲历操作中感受新知.有的内容在一些章节的“途中”,蕴含着一定的逻辑顺序,如“二项式定理”,我们可以从知识的前后联系中创设情境:由多项式法则可以知道(a+b)2、(a+b)3、(a+b)4的三个展开式,你能写出(a+b)n的展开式吗?这样从数学内部创设问题情境,有利于数学活动直达数学本质.
3.例题选编与方法小结——找准“忠”与“创”平衡点
因现在部分学校要求学生课前有预习,课中有时也阅读课本,如果原封不动地给出,学生会感到索然无味.为了提升教材例题、习题的教学功能,需要对课堂的例、习题进行适度改编,有的问题要适当变式,把握其度.
本课的例1可以作如下改编.
观察这两个命题,形式类似,一个为正弦,一个为余弦,称为“对偶命题”,显示对称美、和谐美.
这个是课本上的问题.
例2不用改编,属于难题,右边有个“1”,方向尚明确.如果改成化简,则学生没有方向,更难下手.本例知识、方法的综合性较强,既有正弦、正切两个三角函数名,又有50°,10°两种角,一般是通过“切”化“弦”,消除函数名的差异;通过把asinα+bcosα化为一个角的形式,变为sin40°,即cos50°,出现了2sin50°cos50°,可以逆用二倍角公式,得sin100°,通过互余变换,获得解答.
从课堂反馈,两位老师的小结尚有不足.解题教学,要遵循波利亚的解题表,解题后需要回顾反思,寻求规律,进行小结.其一,解决三角综合问题的基本思想是消除差异,通过三角变换(角变换、名变换及升降幂变换);其二,对于例2的关键点,形如1+tanα的模型,要适
,否则学生印象不深,效果不佳.之后再小结一下解决这类问题的基本方法是“切化弦”,然后通分化为一个角的形式,所谓解决问题的模型思想.
在新授课上,重点是编创好合理的问题链,环环相扣,使学生的探索步步深入.对于这堂类似习题课上,选编、改编好典型例、习题,也是重点,那具有内在联系、层层渐进的例题、练习题,既能巩固知识,构成思维训练问题链,又能提升学生解决问题的能力.另外,需要特别指出的是要理解学生.因为学生是学习的主体,只有关注学情,从学生的学习经验出发,才能准确把握整体框架设计、教学情境创设及适当选择例题习题.如果学校的档次比较高,班级又处于中等偏上的水平,那么在创编能力训练问题链时,就须适当提高教学的密度和难度,增强学生的思维量;如果学生层次低,就必须降低思维要求,增强学生的成功感,让不同的学生在数学上得到不同的发展.
不少数学教师认为这堂三角函数常态课内容单薄、平淡无奇,难以出新、出彩.当同行们阅读完本文后,会有一种不一样的感觉,经过我们上述分析、创编,平淡无奇的“家常课”竟也呈现出饱满、生动、深刻的特点.如果我们在日常的工作中,始终拥有一颗好奇心、探究心,做一个研究者,一直在路上,那么“我们在数学教学工作中所做的一切就都可以变成一种高尚的享受”,提升幸福指数,在这样的工作中永远也不会产生所谓的“职业倦态”.当变式为
1.武瑞雪,黄安成.忠于教材不囿于教材[J].中学数学(上),2010(12).
2.王华民,郑宝生,阮必胜.教师“贴地”而行学生“翩翩”起舞[J].数学通报,2014(5).F
