回归教材,注重开发
——小议复习教学的设计
2017-06-13筅江苏省张家港市塘桥高级中学徐静
筅江苏省张家港市塘桥高级中学徐静
回归教材,注重开发
——小议复习教学的设计
筅江苏省张家港市塘桥高级中学徐静
复习教学是怎么上的?从教师设计的层面来看,笔者发现一个有趣的规律:大都年轻的教师,复习教学中问题的难度越大,而且试题的选择往往千奇百怪,最好是技能超高、难度最大;随着年龄增大,中年教师往往注重知识的系统性,试题难度并不是越难越好,但是问题的层次性呈现得更为恰当;而那些更高水平的名师或特级教师,他们对于问题的设计往往显得更返璞归真,都是以最为简单通俗易懂的问题切入,循循善诱帮助学生理解知识、运用知识.
从近年来高考试题的分析来看,命题专家也尽可能以教材试题为基准,进行深度挖掘,从立足教材出发,通过编制高于教材的试题考查学生的知识运用能力.因此回归教材、注重开发成为近年来教师复习教学的主流设计思路.
一、以概念为本设计
数学概念是高考命题必考的方向,而概念的考查有不少的层次性,既可以是最基本的概念考查,也可以是概念本质的深层次理解,这种考查的复习设计往往需要教师多加以研究并进行复习设计的探索命制.来看一个概念教学的设计.
案例(一)《函数》复习教学设计
设计1(函数概念复习):请学生回顾函数概念,能否用自己的语言描述学过的函数概念?
分析:复习教学的设计要从教材基本概念入手,教师请学生用自己的语言描述,考虑其知识是否真正掌握,属于简单设计.
设计2(函数图示结构):请学生列举函数关系的具体实例和图像.
分析:进一步考查学生知识体系中对于函数实例的掌握程度,主要是让学生掌握函数关系涉及的是“一对一对应和多对一对应”,不存在“一对多对应”,属于简单设计.
设计3(概念本质挖掘):存在函数满足,对任意x∈R都有_____________.(填写符合题意的函数序号)
变式1:函数y=f(x)的定义域为[-1,1],求函数y= f(x+1)的定义域.
变式2:函数y=f(x-1)的定义域为[-1,1],求函数y= f(x+1)的定义域. 4x;④f(sinx)=|x-1|.
分析:利用刚刚回顾的设计2,考查更深层次的函数概念理解.利用设计2考虑怎么样的对应关系可以上升为函数关系?只能是一对一和多对一的对应关系,即这样的对应法则才是函数法则.从设计3来说,笔者显然将问题向前推进了一大步,是典型的基于教材、注重开发编制后的概念问题.学生对于设计3的问题大都显得不太理解,说明其对于函数概念的学习更多依旧停留在表象.其实笔者对于问题的命制是层层递进的,编制设计2恰恰是对设计3做好铺垫的.以④为例,不妨令x=0和x=π,则f(0)=1以及f(0)=π-1,显然对于变量x= 0而言,是一种“一对多”的对应关系,是不可能存在这样的函数关系f(x),其余类似可思考,易得正确答案为②.
设计4(定义域的复习):函数概念中涉及函数三要素,其中最重要的要素是定义域的理解,而定义域的难点在于对抽象函数定义域的复习.给出一系列定义域概念的复习教学设计:
变式3:函数y=f(x)的定义域为[-1,1],求函数y= f(x+1)+f(x-1)的定义域.
变式4:函数y=f(x)的定义域为[-1,1],求函数y= f(x+a)+f(x-a)(a∈R)的定义域.
分析:问题1以具体函数的定义域为切入点,为后续问题做好铺垫.引入变式1~4,思考抽象函数定义域如何求解?主要是两个角度:第一,定义域到底指的是问题中的什么?第二,整体思想的理解和运用是否到位?有了这样的设计,将抽象函数定义域的问题复习到位.
设计5(抽象性质复习):对定义域为R的函数f(x),表达式f(a+x)=f(b-x)与f(a+x)+f(b-x)=0的理解.
分析:从抽象函数的定义域出发,教师设计相关抽象性质的复习,自然而然的引申辐射.从学生掌握来看,学生对上述性质的理解尚不到位,借助图形化手段加强学生对于上述性质的理解.以f(a+x)=f(b-x)为例,对定义域为R的函数而言,即x任意变化情况下,作出其草图如图1所示:
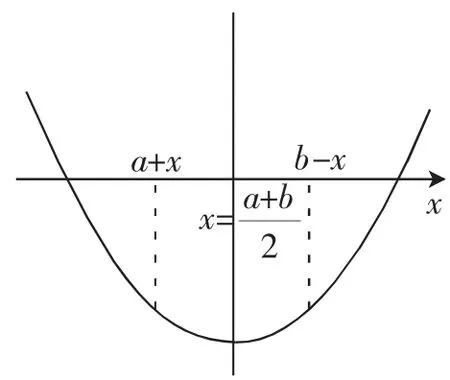
图1

图2
抽象代数式f(a+x)=f(b-x)所表示的含义:自变量x1=a+x与x2=b-x到它们的中间位置距离相等,其函数值也相等,随着x的变化,但是自变量x1=a+x与x2=bx的函数值永远相等,故其运动轨迹如图1所示,函数f(x)的图像关于直线成轴对称.类似地,抽象代数式f(a+x)+f(b-x)=0所表示的含义:自变量x1=a+x与x2=b-x到它们的中间位置距离相等,其函数值互为相反数,随着x的变化,但是自变量x1=a+x与x2=b-x的函数值永远互为相反数,故其运动轨迹如图2所示,函数f(x)的图像关于点成中心对称.
从上述从函数概念出发,笔者进行了层层递进式的概念式复习教学设计,从教材出发、注重了复习的开发,从而让复习教学体现了一定的有效性和高效性.笔者认为,概念式复习教学设计是体现教师对于教材理解力的一种设计,其需要教师关注高考新的形势、以及自身对于数学概念的理解,两者更为有效的结合才能设计更为自然的复习教学.
二、以例题为根设计
以教材例题进行有效的开发,是教师对于知识点运用的一种理解设计.从应试角度来看,不少高考试题的确进行了一定程度的改编,其本质、框架来源于教材例题,这是教师复习教学回归教材、注重开发需要关注的第二个方向.
案例(二)递推数列通项求解
问题2:必修5第69页B组题习题5:“选菜问题”:学校餐厅每天供应500名学生用餐,每星期一有A、B两种菜可供选择.调查资料表明,凡是在这星期一选A菜的,下星期一会有20%改选B菜;而选B菜的,下星期一会有30%改选A菜,用an、bn分别表示在第n个星期选A的人数和B的人数,若a1=300,求a100.
这是典型的线性递推数列求通项模型,其根本是教材试题的体现,经过加工在不少高考真题中出现.
设计1:数列{an}满足a1=1,且an+1=2an+1,求数列an的通项.
分析:利用待定系数法an+1+x=2(an+x),易得x=1,因此数列满足,所以{an+1}是等比数列.这是以教材问题为范本,进行了数据的简单化处理,首先引导学生对于教材问题进行原理上的理解,从而解决教材问题.
设计2:数列{an}满足a1=1,an=2an-1+n-2(n≥2),求通项an.
分析:错解往往是这样构造:an+1+x=2(an+x),根据待定系数法得到x=n-2,因此因此数列{an+n-2}是等比数列,进而求解通项公式.对比正解:令an+λn+ u=2[an-1+λ(n-1)+u],整理得an=2an-1+λn-2λ+u.由待定系数法知所以an+n=2[an-1+(n-1)](n≥2),即{an+n}是以a1+1为首项,2为公比的等比数列,得an=2n-n.
思考错解和正解为什么不同?显然是错解中的整体性构造未达到整体思想,错也是显而易见的,设计2也为后续教师更好地开发做好了铺垫.有兴趣的读者也可以思考下面类似问题:
2015年江苏卷第11题:数列{an}满足a1=1,且an+1-an= n+1(n∈N*),求数列前10项的和.
设计3:数列{an}满足a1=1,an+1=2an+n2,求通项an.
分析:利用设计2的整体性构造思路,令an+1+λ(n+ 1)2+u(n+1)+v=2(an+λn2+un+v),整理得an+1=2an+λn2+(u-2λ)n+v-u-λ.
设计4:数列{an}满足a1=1,an+1=2an+3n,求通项an.
有兴趣的读者可以进一步进行设计和创编.
以教材中的问题为本,进行回归教材的设计和开发,让数学问题不再是孤立的寻求解决,而是进行有效的、高效的以专题形式的探索,这种探索对于学生复习教学而言才是更为高效的,是教师复习教学寻求和探索的.
1.刘兴明.对高一学生函数概念理解的调查研究[D],2008.
2.刘长春.在数列教学中实施变式教学[J].数学教学,2013.
3.殷伟康.数学课堂教学中追问的特征与时机[J].数学教学研究,2013.
