非周期性行业Beta系数跨期时变特征及估值研究

陈蕾 王敬琦

资本资产定价模型采用Beta系数对资产的系统性风险进行度量，在公司估值实务中得到广泛应用。作者以医药、纺织服装、食品饮料、传媒、计算机、通信等六个非周期性行业板块收益率及市场平均收益率的周数据和月数据为研究样本，对三个研究假说进行实证检验。研究发现，时间要素设定差异会显著影响非周期性行业Beta系数稳定性，审慎设定时间要素，有利于提高非周期性行业Beta系数稳定性，同时降低系统性风险度量及公司估值误差。

一、引言

资本资产定价模型（Capital Asset Pricing Model,CAPM）采用 Beta系数对资产的系统性风险进行度量，在公司估值实务中得到广泛应用。但大量实证研究表明，在跨期条件下Beta系数具有时变性特征。国内外学者亦围绕Beta系数跨期时变这一热点命题，对Beta系数在跨期条件下的稳定性（ Brooks et al, 1994[1]; 沈艺峰、洪锡熙，1999[2]；苏卫东、张世英，2002[3]； 赵景文，2005[4]）和时变路径（Kolb and Rodriguez, 1989[5]; 丁志国等，2007[6]；苏治等，2008[7]）进行实证分析，对Beta系数跨期时变的影响因素及成因进行理论揭示（ 陈浪南、屈文洲，2000[8]；丁志国等，2012[9]）；不过部分实证研究的观点和结论存在分歧，这与多样化的研究样本、研究期限、研究方法等不无关系（Jensen, 1969[10]; 丁志国等，2012[9]；陈蕾、王敬琦，2016[11]）。

值得注意的是，多数研究随机选取若干个股作为实证检验样本，不利于剔除单个企业微观因素的干扰，也忽视了可能存在的行业差异；只有个别研究从行业视角对Beta系数时变及其间差异进行探讨；而涉及Beta系数跨期时变与特定行业系统性风险度量或公司估值的关联研究更不多见（陈蕾、王敬琦，2016[11]）。王荆杰（2009）[12]采用滚动回归方法和行业日收益率数据发现，Beta系数稳定性较差的前五个行业中，有三个是周期性行业，可能是较强的周期性导致产生波动较大的系统性风险；丁志国等（2012）[9]采用7种实证方法和行业日收益率数据，对中国、美国、英国、日本证券市场的分行业Beta系数跨期时变特征进行检验。在此基础上，陈蕾、王敬琦（2016）[11]指出，不同的研究设计使“Beta系数是否稳定”不可一概而论，并进一步以有色、钢铁、石化、房地产、银行等5个周期性行业板块收益率及市场平均收益率的周数据和月数据为研究样本，提出：当运用回归方法估算Beta系数时，对于回归样本选择所涉及的回归期限和收益率度量时限这两项时间要素，其设定差异会显著影响Beta系数稳定性，进而对系统性风险度量及公司估值结果影响显著；审慎设定时间要素，有利于提高Beta系数稳定性，同时降低系统性风险度量及公司估值误差；“5～10年”是更为可取的Beta系数估计时段，并应优先选择以“周”为单位的收益率度量时限，其次是以“月”为单位。这对于之前的研究结果，既是验证和延伸，又是探索与创新，一定程度上深化了现有公司估值理论中的系统性风险度量研究。但陈蕾、王敬琦（2016）[11]也强调，其研究重点以波动性较强的周期性行业为检验样本探寻规律，相关结论是否具有普适性还有待进一步验证，未来研究亦可选取非周期性行业样本进行拓展。

应该看到，较之周期性行业，非周期性行业（亦可称为“弱周期性行业”）的收益波动对宏观经济变化敏感度较弱，既涉及食品、医药等与人类日常消费息息相关的防守型行业，又涉及计算机、通信等依靠技术进步得以发展的增长型行业。那么，非周期性行业是否因为受宏观经济变化影响较小而具有波动性较小的系统性风险，即Beta系数不具有跨期时变特性？时间要素设定差异，是否会对非周期性行业的系统性风险度量及公司估值结果产生显著影响？如果影响显著，应如何对时间要素进行设定以提高非周期性公司估值合理性和准确性？这些问题值得进一步探究。全文余下部分做如下安排：第二部分为研究设计，第三部分为样本数据与描述性统计，第四部分为实证结果及分析，第五部分为结论。

二、研究设计

（一）研究假说

结合Beta系数定义，作为一种系统性风险指数，Beta系数可以度量一种证券或一个投资证券组合相对总体市场的波动性。尽管非周期性行业景气度受宏观经济影响较小，但是，收益波动对宏观经济敏感度低尚不能与系统性风险波动性低简单划等号。由此，本文综合已有经验研究证据，暂假定陈蕾、王敬琦（2016）[11]的研究结论具有普适性，并具体提出三个可供检验的假说：

假说1：时间要素设定差异会显著影响非周期性行业Beta系数稳定性。

假说2：时间要素设定差异会显著影响非周期性行业系统性风险度量及公司估值结果。

假说3：审慎设定时间要素，有利于提高非周期性行业Beta系数稳定性，同时降低系统性风险度量及公司估值误差。

其中，为便于与已有研究（陈蕾、王敬琦，2016[11]）结论进行对照比较，本文将继续设定与之相同的研究期限进行实证检验；在研究方法上，除采用Chow检验等相同研究方法外，还将尝试CUSUMSQ检验用以比较。

（二）检验对象与回归样本

本文拟重点以我国沪深A股市场中非周期性行业作为检验对象；具体选择“医药、纺织服装、食品饮料”等3个防守型行业和“传媒、计算机、通信”等3个增长型行业，共计6个非周期性行业样本。同时，继续选取10年长度测算区间作为样本回归期限，选用“周”和“月”为单位作为回归样本的收益率度量时限；样本数据时间跨度从2005年1月1日至2014年12月31日，共计3042个周样本和720个月样本。通过将此样本周期划分为不同时间段，还可形成若干样本子集，以便对研究假说进行检验。

（三）研究方法

本文采用的研究方法分为四个主要步骤：

第一步，通过普通最小二乘法（Ordinary Least Square,OLS）分别考察、比较不同回归期限（1～10年）和收益率度量时限（“周”和“月”）下的6个样本行业Beta系数估计值与动态轨迹；随后，使用标准差和平均绝对偏差（Mean Absolute Deviation, MAD）值初步检验Beta系数稳定性。

其中，对Beta系数进行估计时，采用单指数市场模型，即：

式中， Rt为资产期望收益率；Rm为市场组合期望收益率；β为资产Beta系数。

根据式（1），引入一元一次方程式（2）和式（3）：

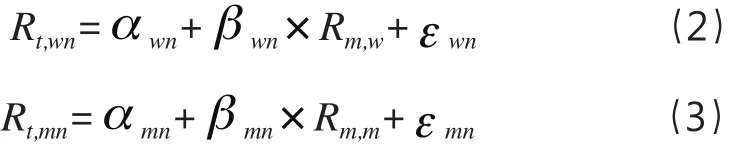
式（2）和式（3）中，Rt,wn和Rt,mn分别表示样本行业周收益率和月收益率，Rm,w和Rm,m分别表示市场平均周收益率和月收益率，βwn和βmn分别表示收益率度量时限为“周”和“月”的样本行业Beta系数，αwn和αmn为常数项，εwn和εmn为零均值的随机误差项，n代表医药、纺织服装、食品饮料、传媒、计算机、通信等不同样本行业。

第二步，利用Chow检验对所估算出的Beta系数进行稳定性检验。本文以每年年末为两段估算时期间的假定断裂点，将10年周期分割为两期，通过Beta系数观测值进行稳定性检验。该检验首先建立如下假设：

原假设：H0:β1=β2，β1、β2代表每个假定断裂点前后两期分别估计的Beta系数；

备择假设：H1:β1≠β2。

在5%的显著性水平下，若统计量F值大于临界值、伴随概率小于显著性水平，则拒绝原假设并接受备择假设，说明两个模型不属于同一个回归模型，即Beta值不稳定。

第三步，利用CUSUMSQ检验对所估算出的Beta系数进行稳定性检验。CUSUMSQ检验采用递归最小二乘法原理，通过递归误差系列构建累积平方和（CUSUMSQ）指标进行参数的稳定性检验。该统计量均值范围为[0，1]，若存在过大偏离均值水平的现象就表明参数不稳定；即，当CUSUMSQ统计量值位于5%显著性水平下的两条置信带之外，则Beta系数不稳定。

第四步，参照已有研究（陈蕾、王敬琦，2016[11]），当利用DCF模型和CAPM模型进行公司估值时，以股权自由现金流折现模型为例，假设各期现金流固定且公司持续经营，则Beta系数估算误差对公司估值结果的影响可表示为：

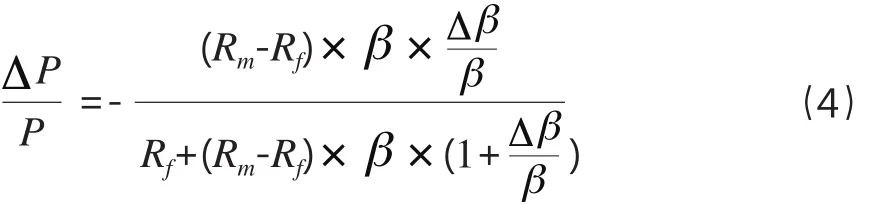
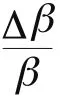
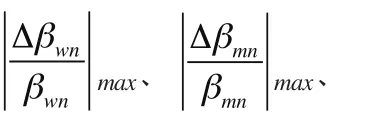
三、样本数据与描述性统计

（一）变量构建与数据来源

1. 行业收益率

本文选择6个样本行业板块股价指数衡量行业收益率，实证数据包括2005年1月1日至2014年12月31日期间板块的周收盘指数和月收盘指数，数据来自于Wind数据库。

根据行业板块周收盘价和月收盘价可以计算得到各行业板块的周收益率和月收益率的时间序列数据。具体计算公式如下：

2. 市场平均收益率

本文选取沪深300指数进行市场平均收益率的计算，具体选取2005年1月1日至2014年12月31日期间的周收盘指数和月收盘指数，数据来自于Wind数据库。

根据沪深300指数的周收盘价和月收盘价可以计算得到周收益率和月收益率的时间序列数据。具体计算公式如下：

（二）描述性统计

利用Eviews8.0软件，对6个样本行业收益率和市场平均收益率的时间序列数据进行描述性统计分析，分析结果详见表1。

根据表1，从2005年1月1日至2014年12月31日期间每个行业周指标各获得507个观测值，每个行业月指标各获得120个观测值。6个行业指数与沪深300指数的平均收益率均为正值，说明这段时间内所研究的这7个指数表现相对较好。其中，通信行业的平均收益率最低，医药行业的平均收益率最高。各类指标的标准差均较大，行业平均收益率离散程度大部分高于市场平均收益率，表明研究时段内股价波动较为剧烈，市场较不稳定。与周收益率相比，月收益率度量下的收益率离散程度明显较高，表现出更强烈的波动性。另外，各类收益率变量的偏度均为负值，但数值较小，说明分布形态与正态分布相比为负偏或左偏，偏斜程度较小；但峰度均为正值，说明分布曲线比正态分布的高峰更加陡峭，呈尖顶曲线。

（三）时间序列趋势分析

根据上述样本数据，利用Eviews8.0软件输出得到各类收益率变量的时间序列趋势图，如图1～图14所示。

表1 变量描述性统计

图1 Rt,w医药时间序列趋势

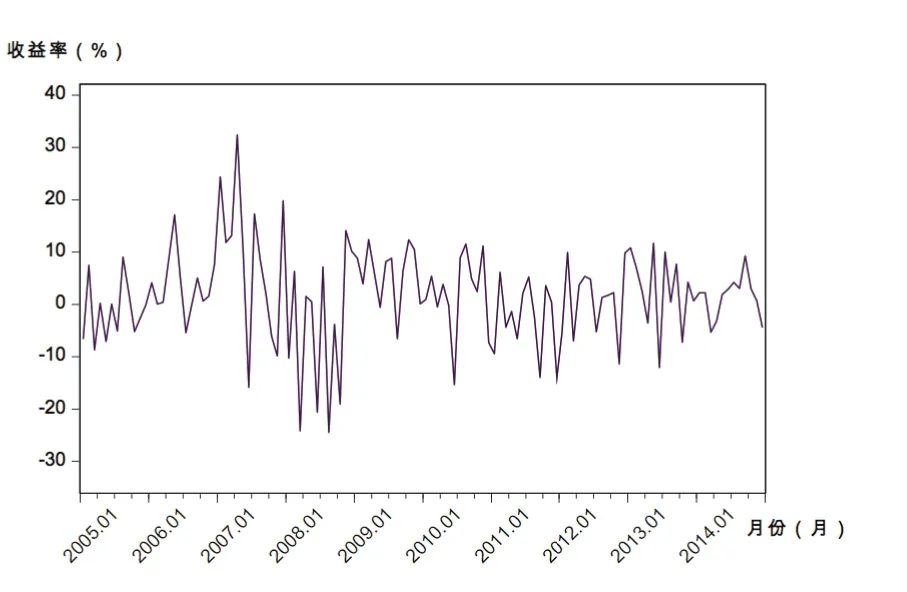
图2 Rt,m医药时间序列趋势

图3 Rt,w纺织服装时间序列趋势

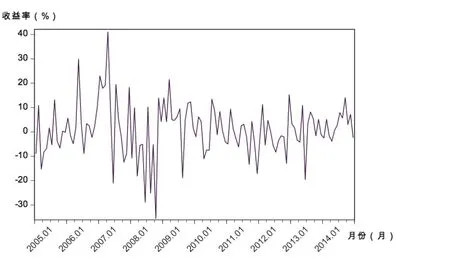
图4 Rt,m纺织服装时间序列趋势

图5 Rt,w食品饮料时间序列趋势

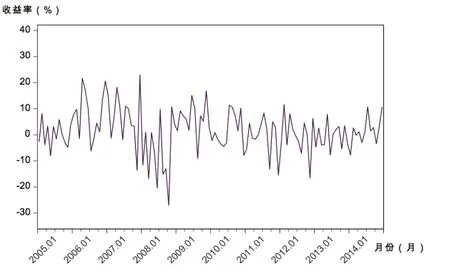
图6 Rt,m食品饮料时间序列趋势

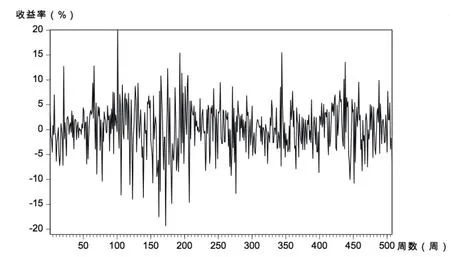
图7 Rt,w传媒时间序列趋势

图8 Rt,m传媒时间序列趋势

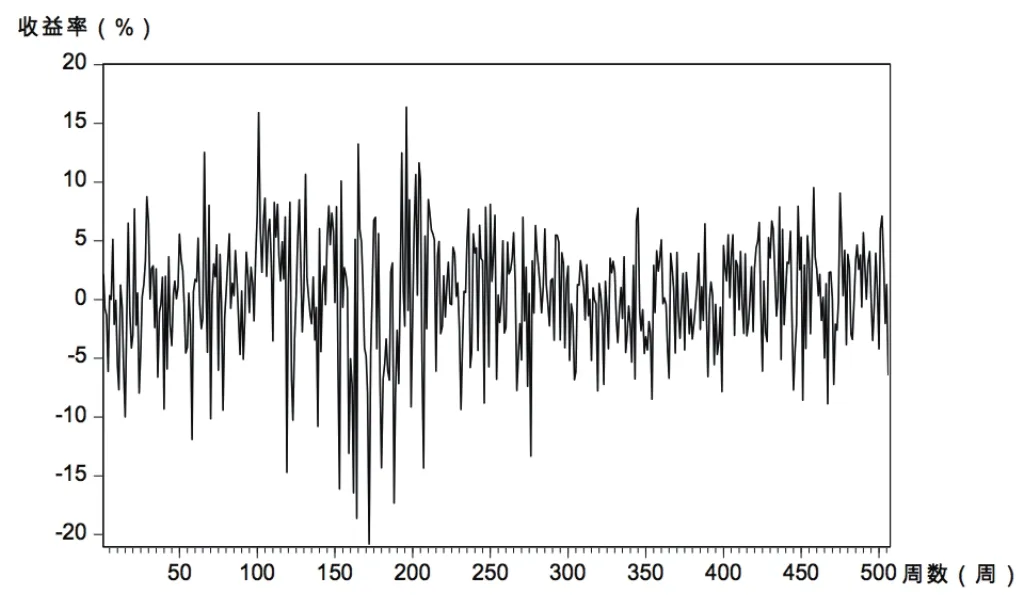
图9 Rt,w计算机时间序列趋势

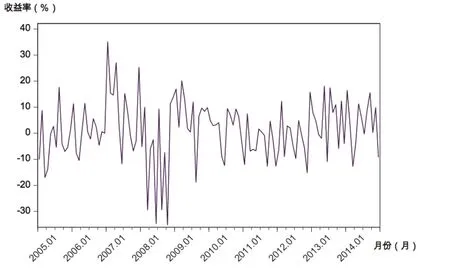
图10 Rt,m计算机时间序列趋势

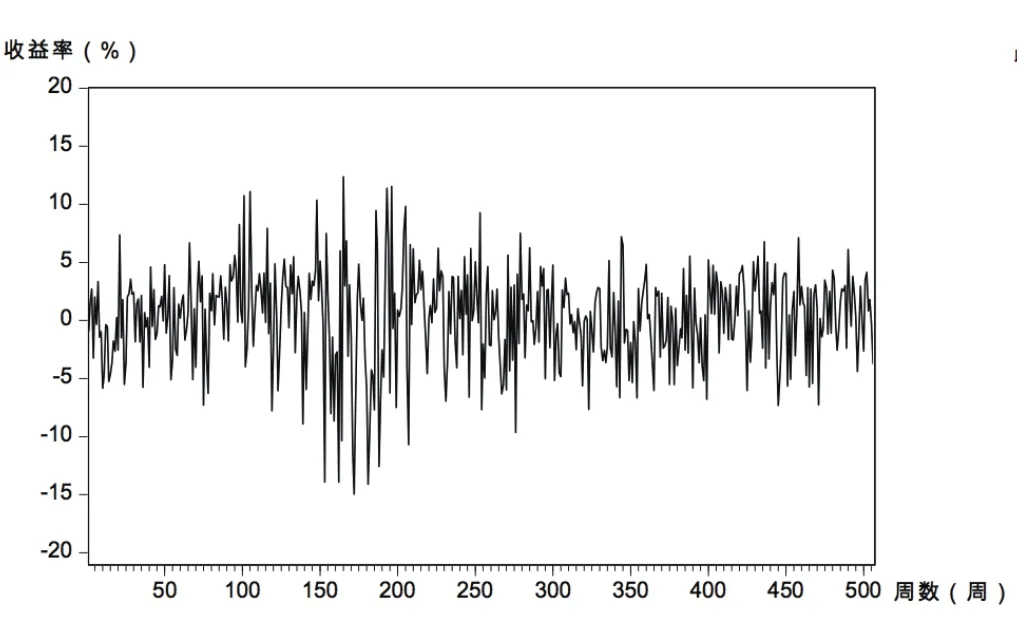
图11 Rt,w通信时间序列趋势

图12 Rt,m通信时间序列趋势

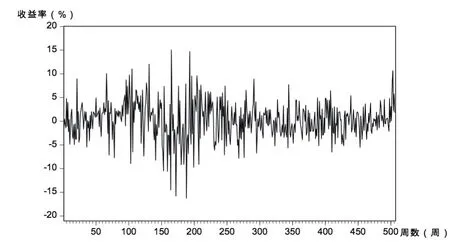
图13 Rm,w时间序列趋势

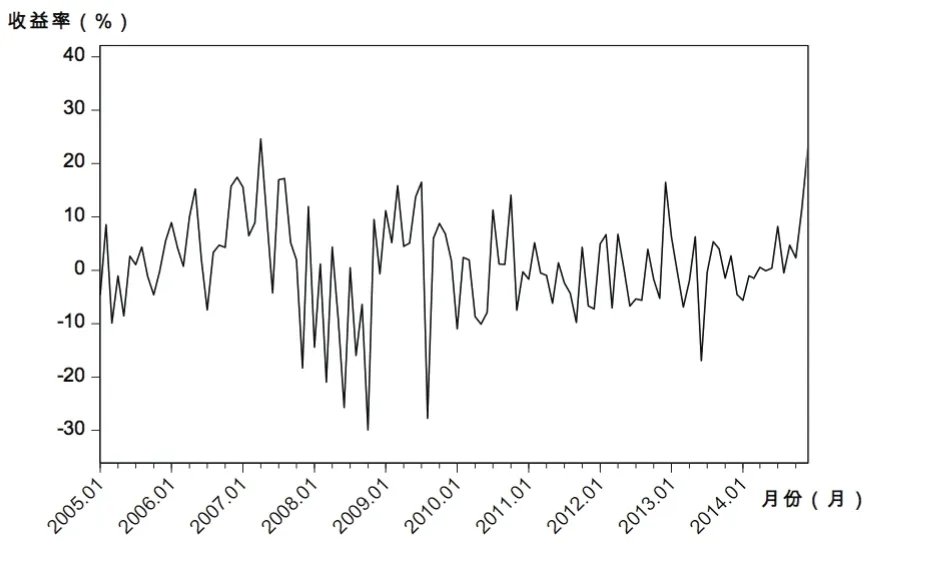
图14 Rm,m时间序列趋势

从图1～图14可见，几个样本行业收益率走势与市场总体相同，经济危机所导致的剧烈波动至220周或2009年初基本达到平稳。从周收益率来看，计算机和纺织服装行业收益率波动较剧烈；传媒行业的收益率更易出现极端值；其余行业收益率变化速度略缓。从月收益率看，纺织服装行业依然很不稳定，波动浮动最大；通信行业、计算机行业在2008年时收益率有较大跌幅，受金融危机影响最大；传媒行业在2013年初到2014年末发生剧烈波动。

四、实证结果及分析

（一）Beta系数动态轨迹与标准差、MAD值稳定性检验

利用Eviews8.0软件，模拟测算得到以2005年1月1日为评估基准日计算的1～10年Beta系数真实值βwn、βmn和以2014年12月31日为评估基准日计算的1～10年Beta系数历史值βwn、βmn，如表2和表3所示。对其中通过显著性水平检验的两种情形下全部βwn、βmn估计结果进行描述性统计分析见表4，并绘制其回归期限变化过程中的动态轨迹见图15～图18。

根据表2～表4、图15～图18可以发现：（1）当回归期限较短时，月收益率下Beta系数估计效果较之周收益率略差，但随着回归期限延长，估算结果可靠性得到提高；（2）βwn、βmn在同一回归期限下估计结果并不相同，且在数值大小方面未呈现显著规律，说明样本行业Beta系数的周收益率估计结果和月收益率估计结果相对独立；（3）从βwn、βmn的波动走势上来看，两种评估基准日测算的Beta值基本上在回归期限为7年（含）以上时趋于稳定，并都趋近于1，表现出收敛趋势；（4）βwn标准差均值、MAD均值分别为0.14和0.11，βmn标准差均值、MAD值均值分别为0.15和0.12，后者数值略高于前者，说明样本行业Beta系数的周收益率估计结果比月收益率估计结果的稳定性略好；（5）各行业当中，计算机行业的Beta系数最不稳定，

通信行业的Beta系数最稳定。综合来看，大部分增长型行业的Beta系数标准差及MAD值低于防守型行业，即防守型行业Beta系数较之增长型行业更不稳定。

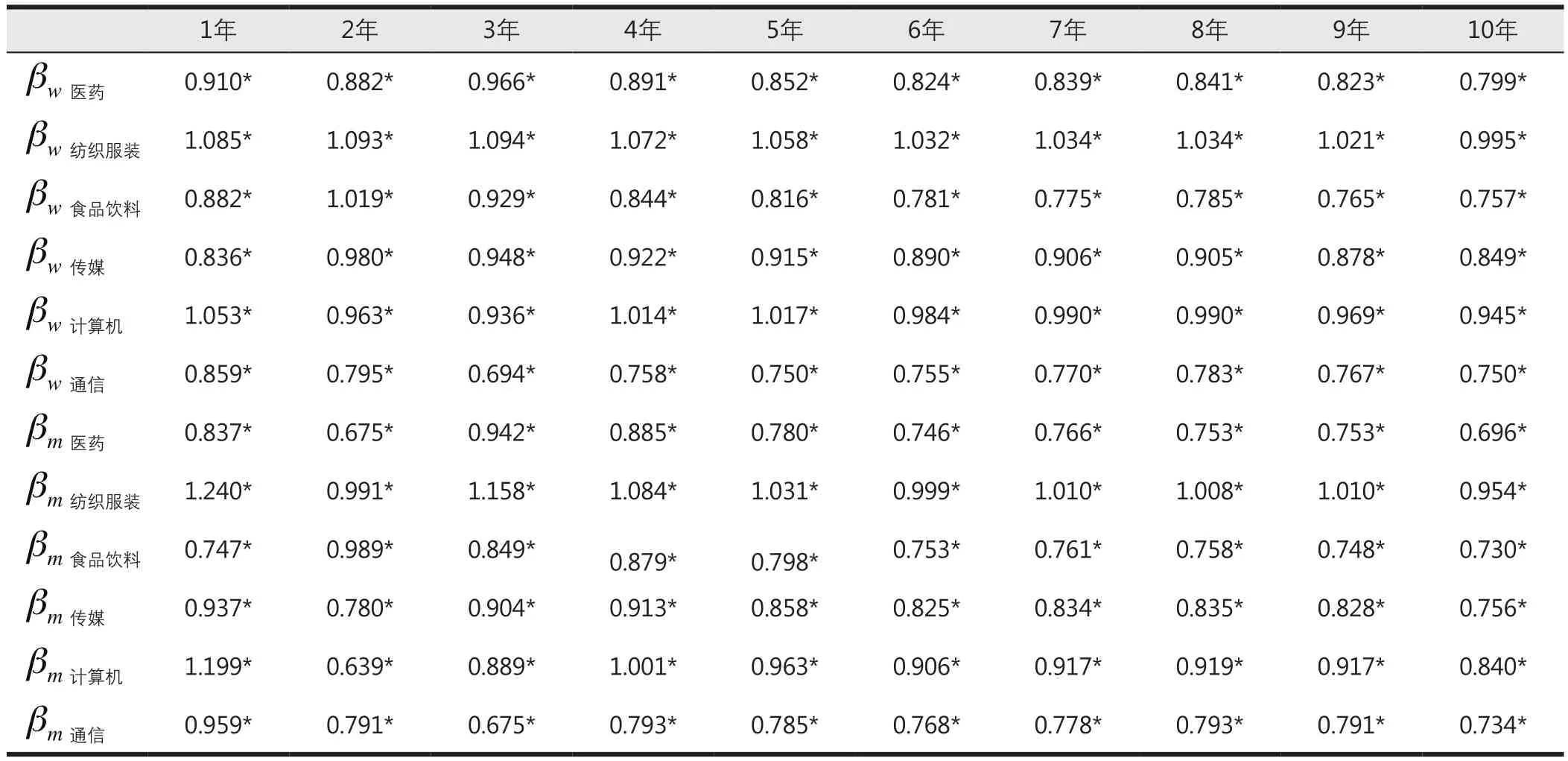
表2 未来1～10年回归期限下真实βwn、βmn观测值（以2005年1月1日为评估基准日）

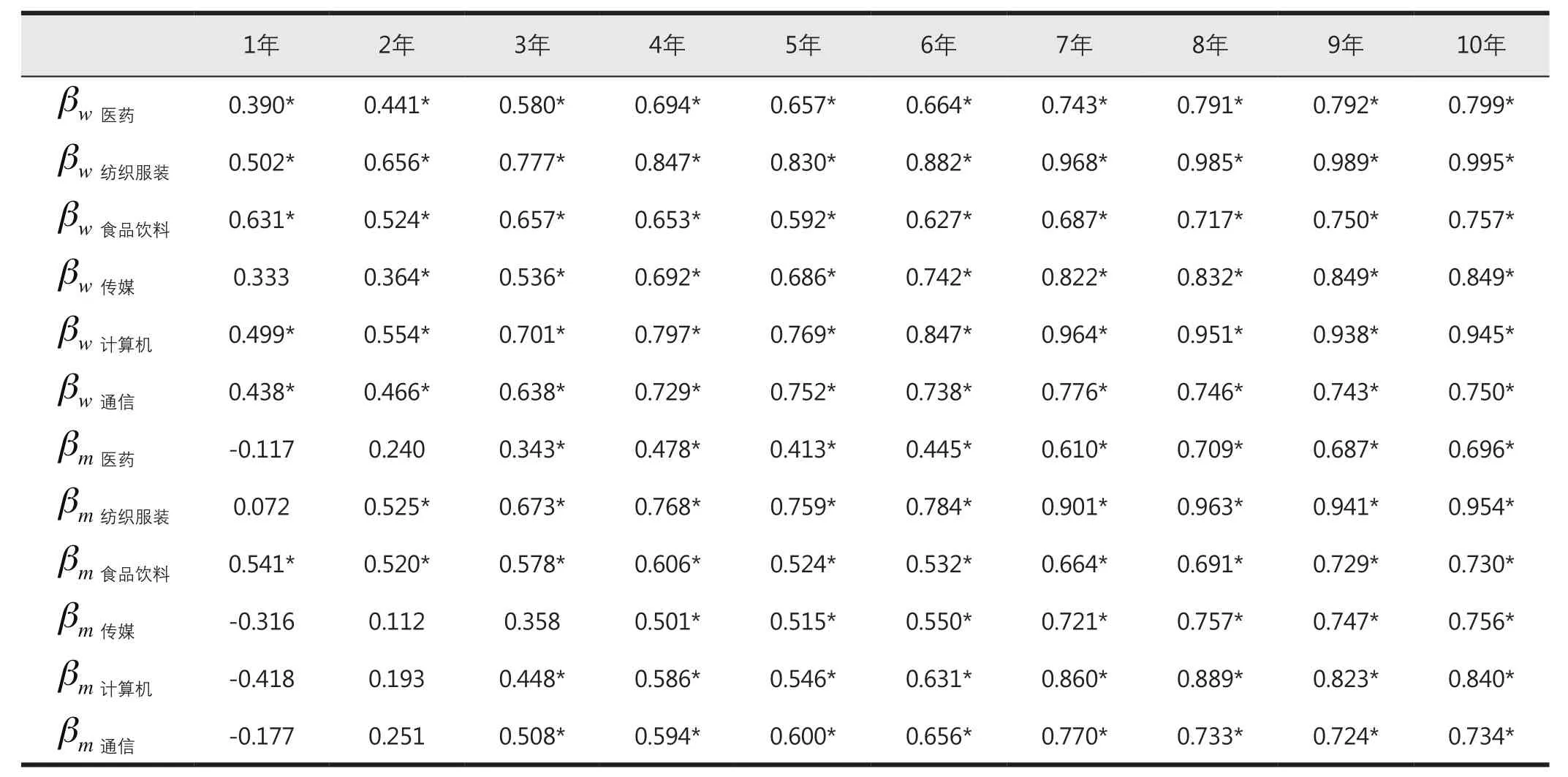
表3 过去1～10年回归期限下历史βwn、βmn观测值（以2014年12月31日为评估基准日）

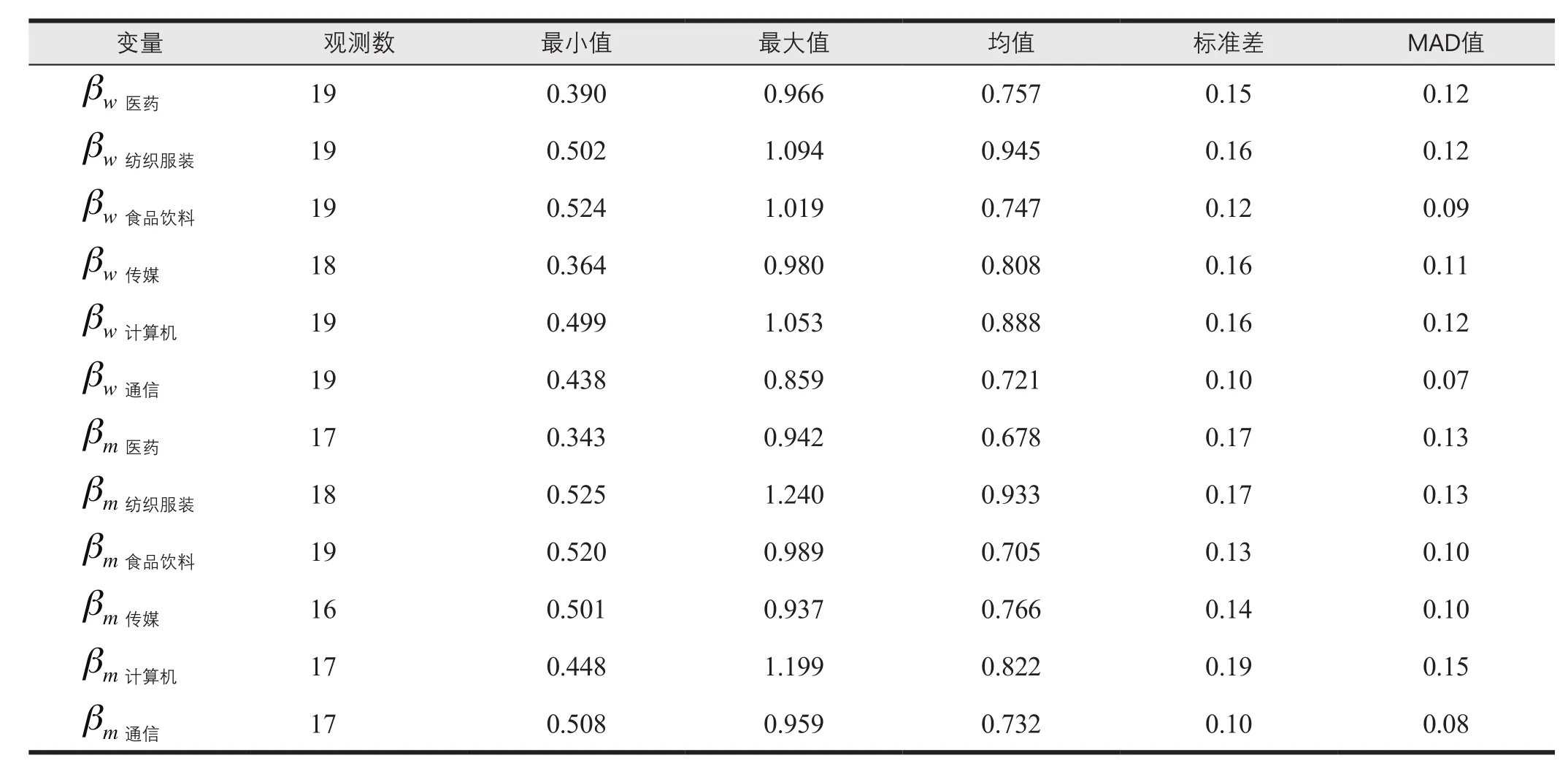
表4 βwn、βmn估计结果描述性统计

图15 2005年1月1日评估基准日真实βwn趋势

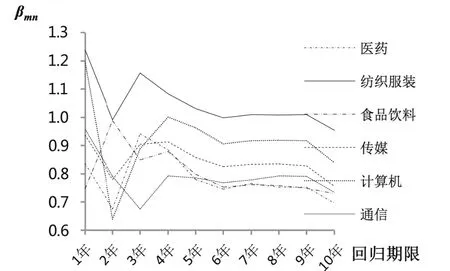
图16 2005年1月1日评估基准日真实βmn趋势

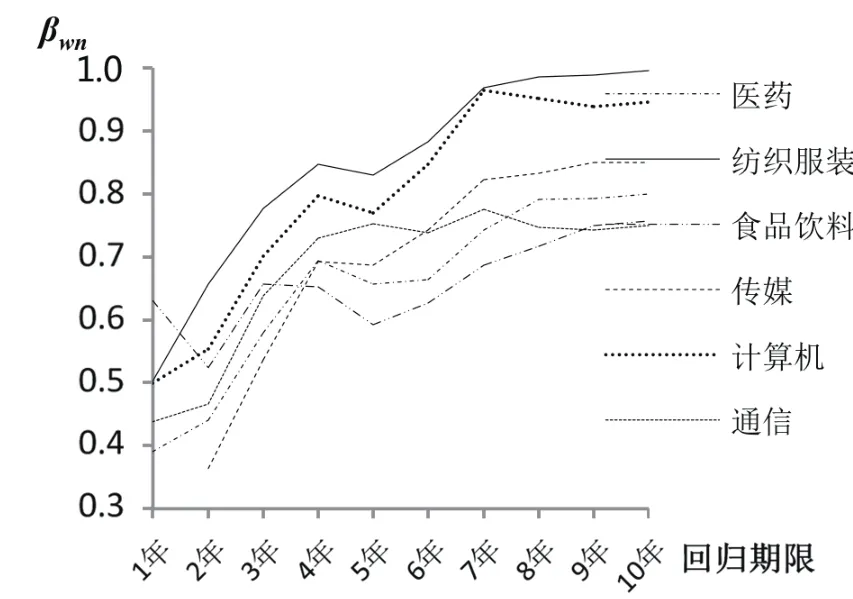
图17 2014年12月31日评估基准日历史βwn趋势

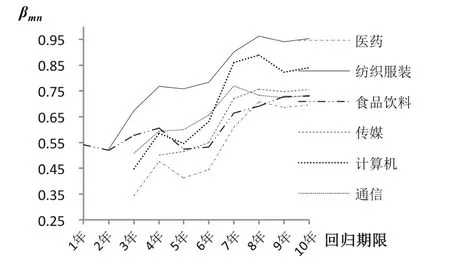
图18 2014年12月31日评估基准日历史βmn趋势

（二）Beta系数的Chow稳定性检验

利用Eviews8.0软件，分别通过Chow检验测算9个断裂点前后两期各行业βwn、βmn稳定性，检验得到的F值如表5所示①评估基准日为2005年1月1日的Chow检验测算结果与评估基准日为2014年12月31日的测算结果相同。。

根据表5可见，在5%的显著性水平下：（1）βwn、βmn的Chow检验结果中，月收益率度量时限下不稳定的Beta系数仅有20.45%，而周收益率度量时限下所估计出的Beta系数呈不稳定性情形的约占50.94%，说明样本行业Beta系数的月收益率估计结果的稳定性略好于周收益率估计结果，这也可能源于前者剔除了更多未通过显著性水平检验的βmn所致；（2）各假定断裂点的Chow检验结果显示，历史回归期限为7年（含）以上时，样本行业Beta系数估计结果的稳定性更好；（3）从行业角度来看，纺织服装行业的稳定性较差，通信行业的稳定性较好。也说明防守型行业的稳定性整体上劣于增长型行业。

（三）Beta系数的CUSUMSQ稳定性检验

继续采用CUSUMSQ检验进一步测算Beta系数稳定性，仍以2014年12月31日为评估基准日，借助Eviews8.0软件输出的周收益率与月收益率下6个行业CUSUMSQ统计量结果见图19～图30。

根据图19～图30可以发现：（1）经比较两种收益率下输出结果，周收益率下统计量溢出置信带现象的行业个数更多，除计算机行业外的其他行业都存在Beta系数不稳定现象，而月收益率中只有纺织服装行业和传媒行业存在统计量溢出置信带现象，进一步说明样本行业Beta系数的月收益率估计结果稳定性总体略好于周收益率估计结果；（2）传媒、纺织服装行业的Beta系数不稳定性最为明显，纺织服装行业在周收益率下出现Beta系数不稳定情况的区间最长，传媒行业在月收益率下出现Beta系数不稳定情况的区间最长；（3）大部分行业在历史回归期限为7年（含）以上时未出现置信带溢出现象，可以认为较长回归期限有利于Beta系数的稳定。可见，CUSUMSQ检验结果与Chow检验结果基本一致，只是在Beta系数稳定性时间段等细节方面略有差异。这可能源于两种方法检验原理不同：Chow检验侧重于假定断裂点变化情况，而CUSUMSQ检验侧重于整个回归时段变化情况。

表5 βwn、βmn稳定性检验（F值）

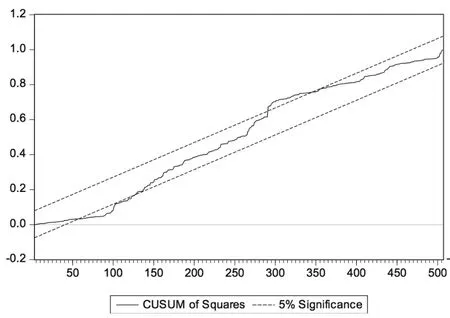
图19 βw医药CUSUMSQ统计结果

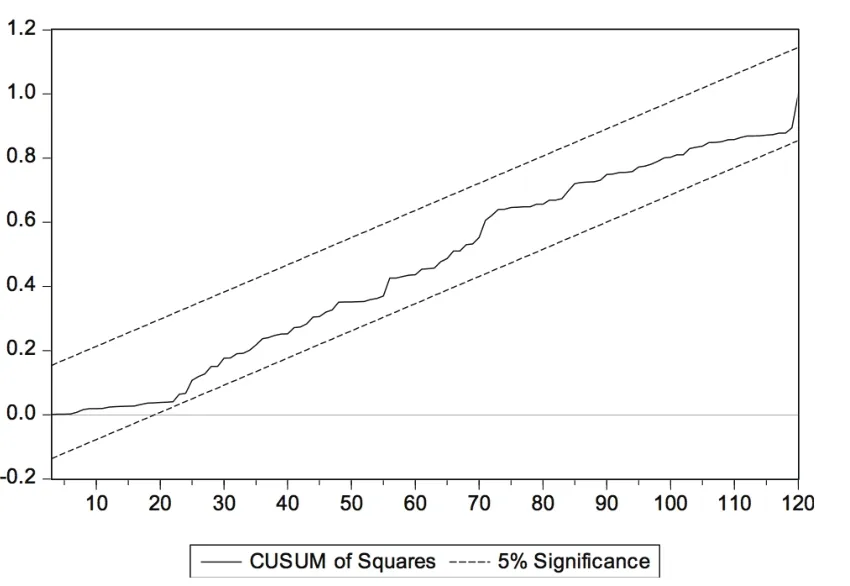
图20 βm医药CUSUMSQ统计结果

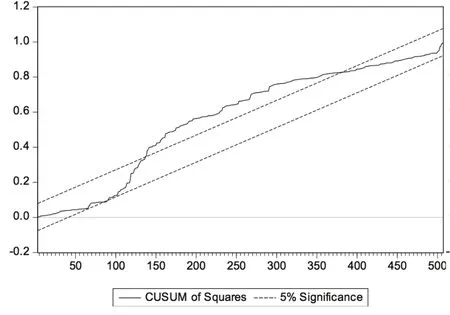
图21 βw纺织服装CUSUMSQ统计结果

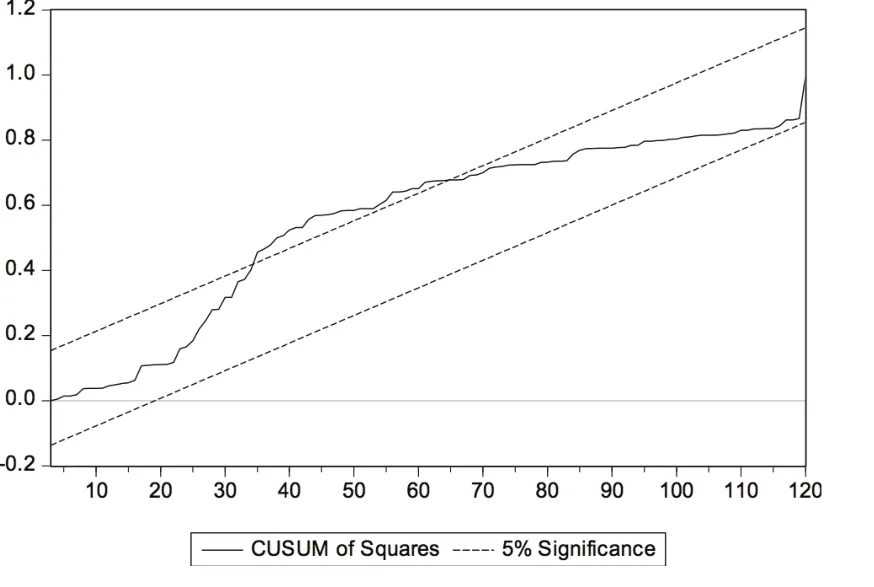
图22 βm纺织服装CUSUMSQ统计结果

图23 βw食品饮料CUSUMSQ统计结果

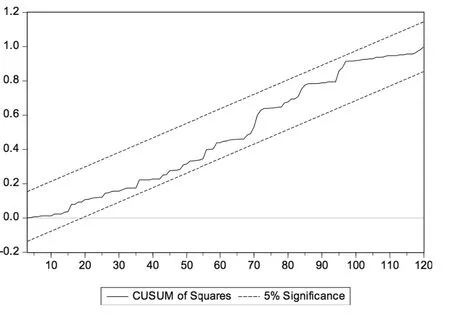
图24 βm食品饮料CUSUMSQ统计结果

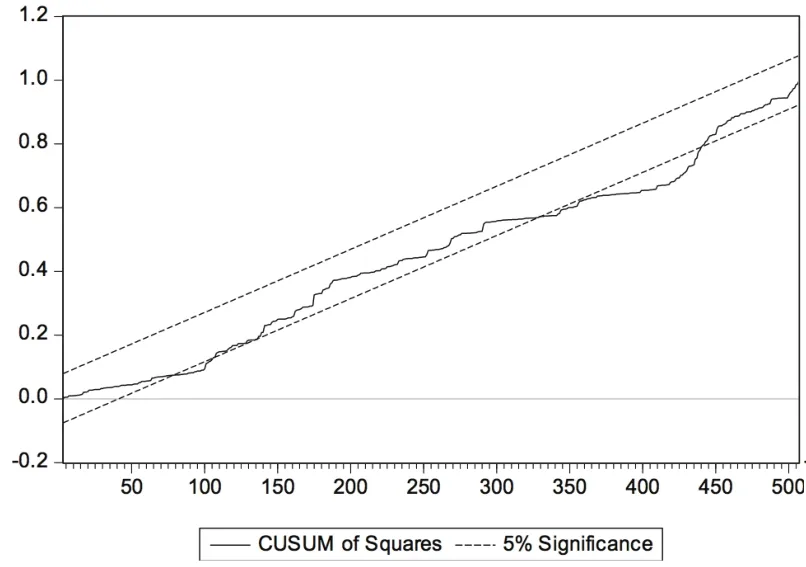
图25 βw传媒CUSUMSQ统计结果

图26 βm传媒CUSUMSQ统计结果

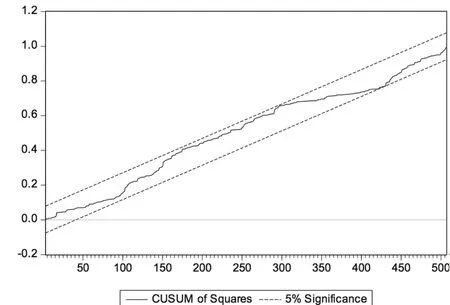
图27 βw计算机CUSUMSQ统计结果

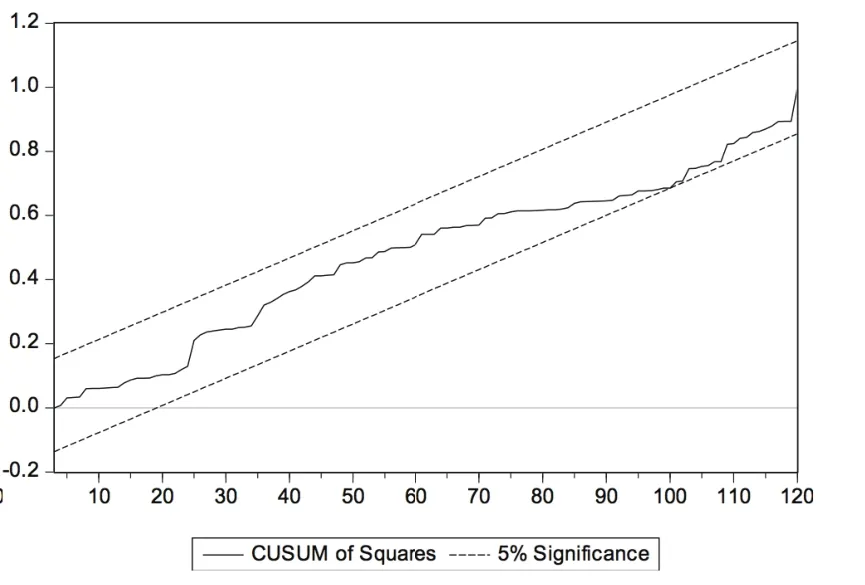
图28 βm计算机CUSUMSQ统计结果

图29 βw通信CUSUMSQ统计结果

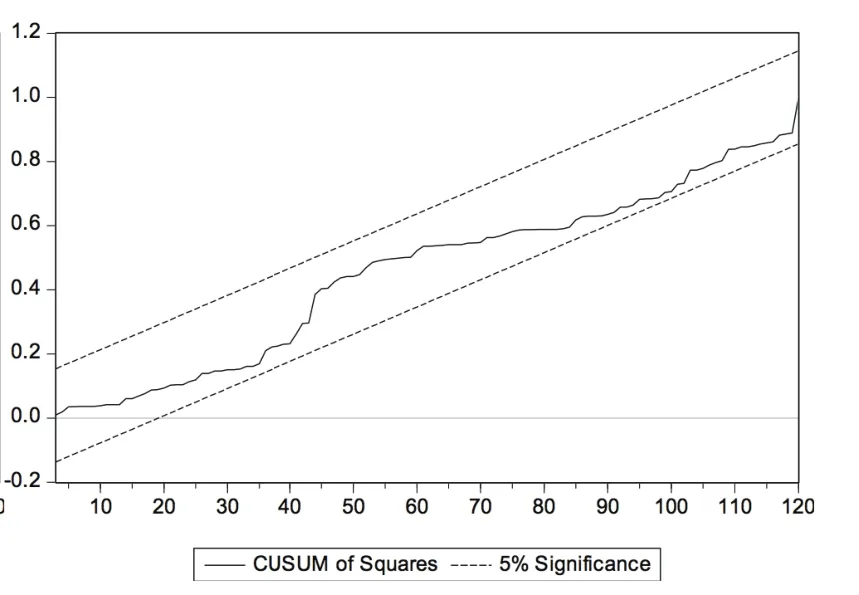
图30 βm通信CUSUMSQ统计结果

（四）对系统性风险度量及公司估值结果影响的实证模拟

若按近十年我国市场历史平均水平②2005～2014年期间，我国一年期银行定期存款利率在2.25%～4.14%范围内浮动，沪深300指数平均年收益率为13.45%。，Rf取值3.00%，Rm取值13.45%，则方程（4）进一步变化为：

根据表3数据和方程（9），继续以2014年12月31日为评估基准日，分别统计各样本行业系统性风险度量及公司估值最大可能误差的实证模拟结果，其中，在不同回归期限（1～10年）和相同收益率度量时限下的结果如表6所示，在相同回归期限（7～10年）③鉴于实证分析前三部分均已证明当回归期限为7年（含）以上时，样本行业Beta系数估计结果具有更好的稳定性，此部分只统计分析各样本行业在7～10年回归期限下的同期误差，以集中考察Beta系数相对稳定情况下不同收益率度量时限对系统性风险度量及公司估值结果可能产生的影响。和不同收益率度量时限下的结果如表7所示。

（五）实证分析结论

综合以上四个步骤的实证结果及分析，总结如下：（1）时间要素设定差异会显著影响非周期性行业Beta系数稳定性。验证假说1；（2）时间要素设定差异会显著影响非周期性行业系统性风险度量及公司估值结果。验证假说2；（3）样本行业Beta系数估计结果在回归期限为7年（含）以上时具有更好的稳定性。Beta系数的周收益率估计结果和月收益率估计结果相对独立，虽然前者的Beta系数估计效果和标准差、MAD值检验得到的稳定性在回归期限较短时略好于后者，但Chow检验、CUSUMSQ检验以及Beta系数对系统性风险度量及公司估值结果影响的实证模拟结果均证明后者的稳定性和精确度总体好于前者。所以审慎设定时间要素，有利于提高非周期性行业Beta系数稳定性，同时降低系统性风险度量及公司估值误差。验证假说3。

表6 不同回归期限（1～10年）和相同收益率度量时限下最大可能误差的实证模拟

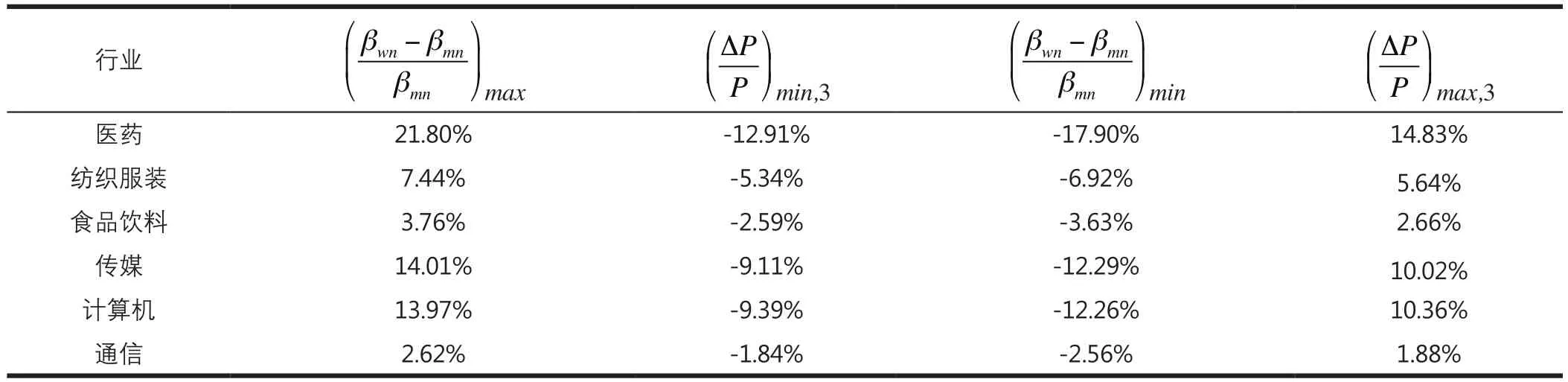
表7 相同回归期限（7～10年）和不同收益率度量时限下最大可能误差的实证模拟

五、结论

本文以2005年1月1日至2014年12月31日为样本周期，以医药、纺织服装、食品饮料、传媒、计算机、通信等6个非周期性行业板块收益率及市场平均收益率的周数据和月数据为研究样本，对三个研究假说进行实证检验，与已有文献结论进行对照研究。研究发现：（1）对于非周期性行业，Beta系数跨期时变、时间要素设定差异同样关系到其系统性风险度量及公司估值结果的精确度；（2）“7～10年”是更为可取的Beta系数估计时段④实证结果表明，样本行业Beta系数估计结果在回归期限为7年（含）以上时具有更好的稳定性，但考虑到Beta系数跨期时变的内生性、回归样本数据规模无限扩大的操作意义、以及关于Beta系数最佳估计时段的现有结论等因素，Beta系数回归期限不宜过长，以7～10年更为可取。，此时应优先选择以“月”为单位的收益率度量时限，其次是以“周”为单位；（3）通过审慎设定时间要素，可以提高Beta系数稳定性，同时降低系统性风险度量及公司估值误差。

与部分已有研究结果相比，陈蕾、王敬琦（2016）[11]研究结论的普适性得到验证，只是在Beta系数最佳估计时段的具体选择方面略有差异：对于周期性行业，回归期限为“5～10年” 、“周”收益率度量时限下的Beta系数估计效果总体更佳；对于非周期性行业，回归期限为“7～10年” 、“月”收益率度量时限下的Beta系数估计效果总体更佳。实证结果也可以证明，样本行业Beta系数估计结果围绕均值1随机发生，并具有收敛趋势，这些结论与已有文献结论一致；并且，非周期性行业中增长型样本行业Beta系数的稳定性整体好于防守型样本行业。

[1] Brooks R D, Faff R W, Lee J H. Beta stability and portfolio formation[J]. Pacific-Basin Finance Journal, 1994, 2(4):463-479.

[2] 沈艺峰, 洪锡熙. 我国股票市场贝塔系数的稳定性检验[J]. 厦门大学学报: 哲学社会科学版, 1999 (4): 62-68.

[3] 苏卫东, 张世英. 上海股市β系数的稳定性检验[J]. 预测,2002, 21(2): 44-46.

[4] 赵景文. 用ADF方法检验中国A股β系数的平稳性[J]. 中央财经大学学报, 2005 (8) : 72-75.

[5] Kolb R W, Rodriguez R J. The regression tendencies of betas: A reappraisal[J]. Financial Review, 1989, 24(2): 319-334.

[6] 丁志国, 苏治, 杜晓宇. 溢出效应与门限特征: 金融开放条件下国际证券市场风险对中国市场冲击机理[J]. 管理世界,2007(1):41-47.

[7] 苏治, 丁志国, 方明. 跨期系数时变结构研究[J]. 数量经济技术经济研究, 2008(5): 135-145.

[8] 陈浪南, 屈文洲. 资本资产定价模型的实证研究[J]. 经济研究, 2000, (4): 26-34.

[9] 丁志国, 苏治, 赵晶. 资产系统性风险跨期时变的内生性: 由理论证明到实证检验[J]. 中国社会科学, 2012(4): 83-102.

[10] Jensen M C. Risk, The pricing of capital assets, and the evaluation of investment portfolios[J]. Journal of business, 1969,42(2): 167-247.

[11] 陈蕾, 王敬琦. Beta系数跨期时变与公司估值[J]. 统计研究, 2016(8): 37-46.

[12] 王荆杰. 深市行业贝塔系数的稳定性与时变性研究[D]. 厦门大学硕士学位论文, 2009.