一道高考题的建模与变式应用

陆少华

(砀山中学，安徽 砀山 235300)



一道高考题的建模与变式应用

陆少华

(砀山中学，安徽 砀山 235300)

对2016年高考理综新课标卷Ⅰ第35(2)题进行建模和变式应用,引导学生高考物理复习要善于归纳,构建一类题型认知和解题方法．

高考题； 建模； 变式应用

题目.(2016年高考理综新课标卷Ⅰ第35题)某游乐园入口旁有一喷泉,喷出的水柱将质量为m的卡通玩具稳定地悬停在空中．为计算方便起见,假设水柱从横截面积为S的喷嘴持续以速度v0竖直向上喷出;玩具底部为平板(面积大于S);水柱冲击到玩具底板后,在竖直方向上的速度变为0,在水平方向朝四周均匀散开．忽略空气阻力．已知水的密度为ρ,重力加速度大小为g．求:

(1) 喷泉单位时间内喷出水的质量;

(2) 玩具在空中悬停时,其底部面积相对于喷嘴的高度．

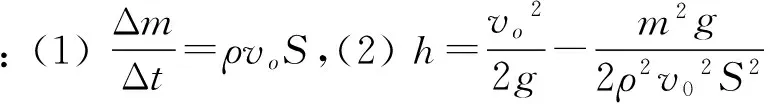
分析:卡通玩具是受到质量连续分布的流体持续作用而稳定地悬停在空中,与质点短暂作用模型不同．为利用已知来探究未知,可以将水流体当作“质量柱体微元”不间断地传递动量．通过分析质量柱体微元的动量传递速率进而求出水流对障碍物的作用力．

1 建立 “质量柱体微元”模型

图1

对于以速度v定向流动的密度为ρ的连续流体,可以在速度方向上选取一段截面积为S的柱体微元．则在Δt时间内通过截面的流体质量就是以高为vΔt、底面积为S的柱体微元的质量．如图1所示,柱体微元质量为Δm=ρSvΔt.

2 变式情景

情景1： 横截面积为S的水柱以恒定的水平速度v持续垂直冲刷竖直墙面,若水柱反弹速率为v′,试求竖直墙面受到冲击力大小．

图2

解析:建立如图2所示质量柱体微元,质量为Δm=ρSvΔt.

柱体微元的动量为

Δp=Δmv=ρSv2Δt.

则单位时间内水流向墙面传递的动量为

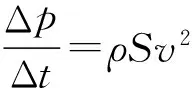
若水流反弹,首先研究因速率变化引起的截面积变化为S′.因为入射水流量Q1等于反射水流量Q2,即

Sv=S′v′.

可得反射水的截面积为

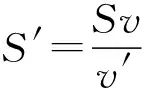
则反射水流带走动量的速率为

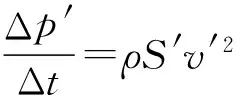
竖直墙面受力为

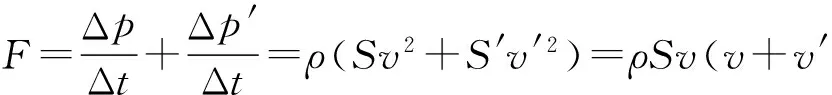
若水流冲刷墙面后便自然沿壁流淌下来,即v′=0，则墙面受力为F=ρSv2.

若水流冲刷墙面后原速返回,即v′=v，则墙面受力为F=2ρSv2.

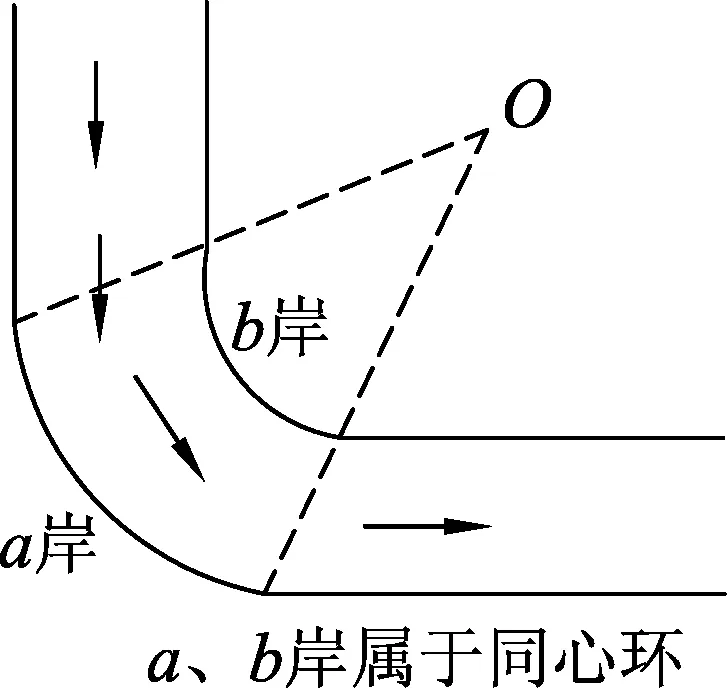
图3

情景2：如图3所示,一河流弯道,弯道a岸、b岸共属同心环,两岸间距为Δr,弯道a岸半径为r．已知河水流速为v,深度为h．试求水流冲刷a岸的压强．

解析:如图4示,在受水流冲刷的a岸边取张角为Δθ的一小段圆弧,由两岸a和b与假想截面c和d构成一“小围湖”．

图4

图5

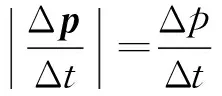
情景3： 水柱从横截面积为S的喷嘴持续以速度v0竖直向上喷出在不同高度处进行截流阻挡,截流后,水柱在竖直方向上的速度变为0,在水平方向朝四周均匀散开．忽略空气阻力．已知水的密度为ρ,重力加速度大小为g．试求平面挡板受水柱冲击的作用力随高度如何变化．

解析:由喷嘴向上距离h高度位置,设水柱速度为v.

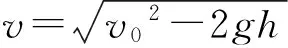
由流量相等得Sv0=S′v.则在距喷嘴向上高度h位置,水柱被截住,动量的传递速率为

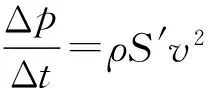
联立以上各式,可得平面挡板所受冲击力为

当水流对卡通玩具冲击力与重力达到平衡时便稳定地悬停在空中．

本例通过构建质量柱体微元模型从传递动量速率角度深层次地分析水流体的冲击力，开阔了视野,拓展了思维．

1 林志建.2016年普通高等学校招生考试全国统一考试·乙卷[J].金考卷特快专递，2016(1):7.

2016-12-02)