运用“思维导图”,让学生学习更具思维含量
2017-06-08朱辉
朱辉

摘 要:思维导图是使师生教与学“可视化”的辅助工具,能够让数学知识结构化、精致化,能够延伸学生的思维触角,发展学生的逻辑思维能力、直觉思维能力等。在数学教学中,教师可以通过“思维导图”让学生的数学思维触手可及、直观展现、有迹可循和集约勾连。运用“思维导图”,学生的数学学习将更具思维含量。
关键词:思维导图;数学学习;思维含量
当下的数学教学已经从“知识能力”取向转向“核心素养”取向。学生的数学核心素养是多元的,但不可否认,“思维品质”应该是核心素养的重中之重。发展学生的思维、培养学生的思维品质,让学生的数学学习更具思维含量是数学教学的根本任务。学生的思维是“不可视”的,面对学生深不可测的大脑“黑洞”,教师有必要借助相应的数学教学方法,让看不见的思维“可视化”。“思维导图”就是显现学生思维发生、引领学生思维发生的工具。
所谓“思维导图”,就是激发学生数学心智的图,包括线段图、指示图、几何图,包括学生画的草图等。思维导图由英国“记忆之父”托尼·博赞先生在20世纪70年代所创,是学生学习的辅助工具,也是教师教学的辅助工具,因此思维导图又称为思维地图、灵感触发图、脑力激荡图等。借助“思维导图”,能够让学生的左右脑协同运作,改善学生的思维模式,让学生“友善用脑”“和谐用脑”“健康用脑”。换言之,“思维导图”主要是借助人的右脑的形象思维来助推左脑逻辑思维的发展、提升。正如德国著名物理学家、思想家爱因斯坦所说,“我不用语言思考问题,而是运用一幅幅能动的、跳动的图像来思考”。“思维导图”的鼻祖托尼·博赞先生盛赞“思维导图”是一把“瑞士军刀”,能够引领人们展开深度思维。在学生数学学习中,“思维导图”既是数学的“知识结构图”,也是学生数学学习的“认知结构图”。借助“思维导图”,学生能够观察、把握、触摸到数学知识的本质,借助“思维导图”,教师能够发掘学生的思维,将学生的数学思维向纵深推进。正是在这个意义上,美国著名图论专家哈里说,“千言万语不及一张图”。在数学教学中,“思维导图”能够鲜活学生的数学感知,增进学生的数学记忆,引领学生的数学思维,激发学生的数学创造。完全可以说,“思维导图”是教师教和学生学的普适性工具,能够让学生产生“思维漩涡”“思维风暴”。
一、借助“思维导图”,让学生的数学思维“触手可及”
学生的头脑是一个“黑匣子”,教学中教师要打开它、运用它、发展它,让学生的数学思维变得“触手可及”,可以借助“思维导图”。“思维导图”作为学生数学学习的支架,能够让学生的数学学习变得直观、可感。学生在“思维导图”的指引下,能够主动地对数学知识进行认知、想象、推理,主动地对数学知识进行建构和整合。
例如:教学《乘法分配律》(苏教版小学数学教材第8册),笔者运用导图让学生产生数学联想,对数学算式进行灵活变换。可以出示“完全开放”的图,也可以出示“半随机半确定”“半混沌半有序”“半直觉半逻辑”“半归纳半演绎”的图,让学生填空,让学生对数、式子等展开全方位的思考、联想。既突出数与乘法分配律的抽象,又能让学生把握其中的数学规律,拓展学生的数学思维。如填数和运算符号的练习:72×(30+6)=72×□+72×□,72×(30+6)=□×30○□×6,72×(30+6)=□○□○□○□等。这样的导图以“完形填空”形式,一方面刺激了学生的大脑,帮助学生由此及彼、由表及里,让学生对乘法分配律的理解逐步走向深刻,另一方面,让学生对乘法分配律的记忆更加牢固、清晰,促进了学生大脑灵感和创意的诞生。
二、借助“思维导图”,让学生的数学思维“直观展现”
学生的数学思维是内隐的、抽象的、跳跃性的。如何让学生的内隐思维变得敞亮、变得直观,可以借助思维导图,将学生思维中不可言说的部分内容“图形化”“示意化”“可理解化”。尤其是解决稍复杂的数学问题时,数学“思维导图”犹如一根拐杖,能够让学生的数学思考从朦胧走向清晰,又犹如一把钥匙,能够开启学生数学问题解决之门。
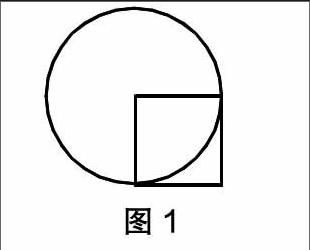
例如:教学《圆的面积》(苏教版小学数学教材第10册),有这样一道题目:如图1,正方形的面积是5平方厘米,求圆的面积是多少?
解决这个问题时,许多学生都理不清头绪,于是笔者运用思维导图,导引学生的数学思维,让学生的数学思维过程得到直观展现。
师:我们要解决什么问题?
生:求圆的面积。
师:要求圆的面积,必须知道什么?
生1:圆的半径。
生2:圆的半径的平方。
师:正方形和圆之间有着怎样的关系?
生3:圆的半径是正方形的边长。
师:正方形的面积公式是什么?
生4:S=a2……
接着,笔者绘制了一张思维导图(如图2),借助思维导图,学生能够在头脑中联结题目中的条件和问题,产生顿悟或灵感。同时,学生的数学思维也在导图中得到体现。
通过“思维导图”,学生对数学问题展开主动思考、主动建构。“思维导图”改变着学生的认知方式、让学生积极主动地投入到数学学习之中,让学生的数学思维变得更有生机与活力。
三、借助“思维导图”,让学生的数学思维“有迹可循”
“思维导图”有助于学生衔接知识,疏通思路。教學中,教师通过“思维导图”对数学学习给予指导,开拓学生的创造性思维。在“思维导图”中,我们能够看到学生思维的方向、路径和状态,灵活调整自己的数学教学,进而更有效地激发学生的数学思维。
例如:教学《角的分类》(苏教版小学数学教材第7册),在学生认识了锐角、直角、钝角、平角和周角后,笔者从角的度数出发,运用“思维导图”,使角的分类相关知识得到了直观、全面的展示(如图3)。学生从“思维导图”出发理解了角的定义、角的分类以及各种角之间的关系等,学生的数学思维变得“有迹可循”。
在这样一个“思维导图”中,从锐角出发,逆时针方向旋转依次得到了锐角、直角、钝角、平角、优角和周角。其中周角和平角、直角之间的关系显明。因为这些角的度数是确定的,而其他角的度数则是不确定的,但尽管不确定,却是存在着范围的。教学中,教师可以引领学生“我图画我心”,让学生尝试自己画出知识结构草图,提高学生对数学知识的归纳、概括能力。
四、借助“思维导图”,让学生的数学思维“集约勾连”
“思维导图”为教师进行教学设计和学生数学问题的解决提供了支持和帮助。教学中,借助“思维导图”,能够让零散的数学知识“精致化”“结构化”“集约化”。通过“串联成线”“连接成片”“构筑成网”,将数学的知识进行有效整理和归纳。在这个过程中,学生的数学思维从“粗放”走向“精致”、从“散点”走向“集成”与“简约”。
例如:复习《三角形、平行四边形和梯形》(苏教版小学数学教材第8册),笔者运用韦恩图、集合图等,帮助学生厘清数学知识的内在脉络。如四边形中,平行四边形是四边形,平行四边形的对边相等、平行,平行四边形的对角相等。而长方形属于平行四边形、菱形属于平行四边形,正方形既是长方形又是菱形。据此,学生建构了这样的“思维导图”(如图4)。
在上面的“思维导图”中,平行四边形、長方形、菱形和正方形的相关知识不仅仅被学生作为定义、性质、判定的理解而存在,而且被作为学生的思维对象而存在。在这里,平行四边形、长方形、菱形和正方形的关系通过“思维导图”一目了然。“思维导图”作为学生数学思维的载体,能够让学生展开“数学化”思考,如平行四边形的对边有怎样的特征?对角怎样?什么样的四边形是平行四边形?什么样的平行四边形是长方形,什么样的平行四边形是菱形?什么样的长方形是正方形?什么样的菱形是正方形等。
作为一种数学教与学的工具,“思维导图”是学生数学思维的路线图,是学生数学思维的“导航仪”。“思维导图”的种类很多,有树状图、线状图、几何图、示意图、集合图等。它改变了学生的认知方式、思维方式。通过“思维导图”,一方面能够建构完整的知识体系、知识网络,在这个网络中,每个数学知识都是一个“节点”,学生可以很方便地把握知识的各个节点(如链接点、生长点、关键点等);另一方面,“思维导图”能够延伸学生的思维触角,引导学生展开发散性、开放性的数学思维,在这个过程中,学生的直觉思维能力、逻辑思维能力等都能得到有效提升。
