基于Deform-3D异形模孔应力集中规律的定量研究
2017-06-06辛选荣河南洛阳秦汉精工股份有限公司
文/辛选荣・河南洛阳秦汉精工股份有限公司
王凌浩・广东理工学院
基于Deform-3D异形模孔应力集中规律的定量研究
文/辛选荣・河南洛阳秦汉精工股份有限公司
王凌浩・广东理工学院
实际生产中,影响挤压成形生产效率和效益最重要的一点就是挤压模具的寿命,而模具的寿命又最终取决于模具受力的应力状态。传统的模具应力研究主要是基于拉梅(Lame)公式的回转体凹模应力分布研究,这种研究方法计算较复杂,而且应力体现不直观,对于一些非回转体模具则不适用。
本文以正方形凹模型腔为例,利用有限元模拟软件,首次在模具应力集中研究中引入理论应力集中系数(KT),创新性提出拟合模具拐角处的圆角半径值(R)与其应力集中程度(KT)的函数关系,将异形凹模应力集中的研究从以往的定性水平提高到定量水平,并为复杂模具应力集中研究提供新的方法和思路。
研究内容及方法
研究试验在仿真模拟软件(Deform-3D)上进行,先进行挤压模拟,然后对挤压后的模具进行应力计算,随后对模具应力分布情况进行分析研究。由于研究的主要内容是凹模型腔拐角处应力集中情况,挤压凹模采用整体式,设置凹模型腔横截面为正方形。考虑到试验方案的完整性,拐角处圆角半径值逐渐增大,直到凹模型腔横截面为圆形,此时凹模型腔不存在拐角,也不存在应力集中,试验方案如表1所示。

表1 试验方案
凹模型腔高为120mm,凹模外径尺寸与型腔长宽对角线尺寸的比值为4:1,为了降低材料硬度对模拟结果的影响,模拟坯料采用纯铝;为了提高模拟效率,材料直接充满凹模,上下凸模同时进行的挤压;考虑到不同变量因子间的对比,挤压力采用静载荷,也就是说挤压力保持不变,模拟时设置为固定值(如120t),温度设置为室温。挤压方式1/2示意图如图1所示。

图1 挤压方式
在运用Deform-3D对模具进行应力计算时,需要将模具视为弹性体,然后通过插值计算的方法将坯料上的成形力映射到模具上,从而来计算模具应力。在这个过程中需要对容差值(Error Tolerance)这个重要参数进行设定,这在一定程度将影响映射和计算的精度。容差值越大,由坯料映射到模具上的力就越精确,但计算时间也随之增长,合理的容差值要参考最小及最大网格尺寸,这样得到的插值计算力能趋于稳定且计算时间相对不长,提高了计算效率。因此,结合实际情况,本文在模具应力计算时容差值设定为0.4。

图2 分析路径
模具应力计算完成后,分析时需根据计算结果选取最大应力值横向截面路径,由于模具是对称的,以拐角处为对称点选取1/4即可,如图2所示。
路径选取完成后,将其应力分布情况通过Deform-3D软件导出,然后进行分析研究,如图3所示。
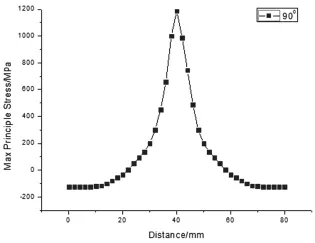
图3 应力分布
模具应力研究的一个重点就是应力集中的研究,其中的一个重要参数KT(理论应力集中系数),是一个大于1的系数,反映了应力集中的严重程度,如公式1所示。
公式1:
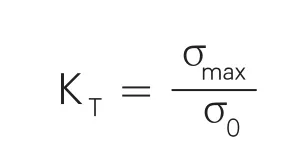
式中:σmax—最大局部应力;σ0—名义应力。参数示意如图4所示。

图4 应力参数示意图
关于公式1和图4所示的理论应力集中系数(KT),目前大多被用于描述板材拉伸试验中的应力集中情况。研究发现,冷挤压模具拐角处应力集中的研究是可以引入KT的,通过引入KT,结合有限元软件,可以很好地将模具复杂的应力集中情况高度的概括,并简单明了地进行表达,为模具应力集中的定量研究建起一座桥梁。
由图3导出结果可以看出,模具在拐角处出现明显的应力集中,可以将其最大值视为σmax;模具型腔内壁侧压力则趋于平稳,变化不大,可以将其视为名义应力σ0。对模具进行理论应力集中系数的计算,其中最大应力σmax=1188MPa,名义应力即内壁侧压力σ0=120MPa,代入公式1得KT=9.90。
试验结果及分析
⑴试验结果。
按照上文方法,导出正四边形(边长为60mm)模具拐角为90°,R1,R2,R4,R8和R16时选取的路径应力分布,如图5所示。
导出正四边形(边长为80mm)模具拐角为90°,R1,R2,R4,R8和R16时选取的路径应力分布,如图6所示。
⑵理论应力集中系数的计算及分析。
按照上文导出的结果可以看出,模具在拐角处都出现明显的应力集中情况,并且型腔内侧壁应力都趋于平稳,对冷挤压模具进行理论应力集中系数计算,设正四边形(边长60mm)模具计算结果为KT1,正四边形(边长80mm)模具计算结果为KT2,结果如表2所示。
将模具拐角为90°时的R值设置为0,对比表2中两种模具的σmax,如图7(a)所示;对比表2计算结果KT1和KT2,如图7(b)所示。
由图7(a)、(b)可以看出,同一尺寸模具,随着拐角处圆角半径的不断增大,拐角处的σmax值是不断减小的,其对应的KT值也是不断减小的,这表明随着圆角半径的不断增大,模具拐角处的应力集中程度是不断降低的。图7(a)表明,随着圆角半径值的不断增大,拐角处最大应力值σmax呈线性不断减小;图7(b)表明,随着圆角半径值不断增大,拐角KT也呈线性不断减小,且两种模具的线性减小趋势重合,这说明不同边长模具,同一拐角半径,拐角KT是不变的,即应力集中程度是相同的,这表明圆角半径值是影响模具型腔拐角应力集中程度的决定因素,而与模具边长无关。

图5 路径应力分布
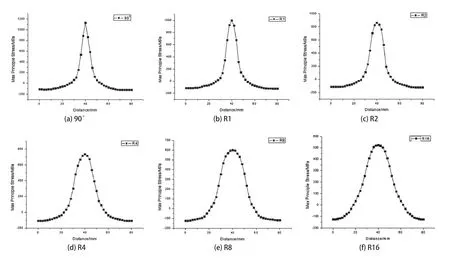
图6 路径应力分布
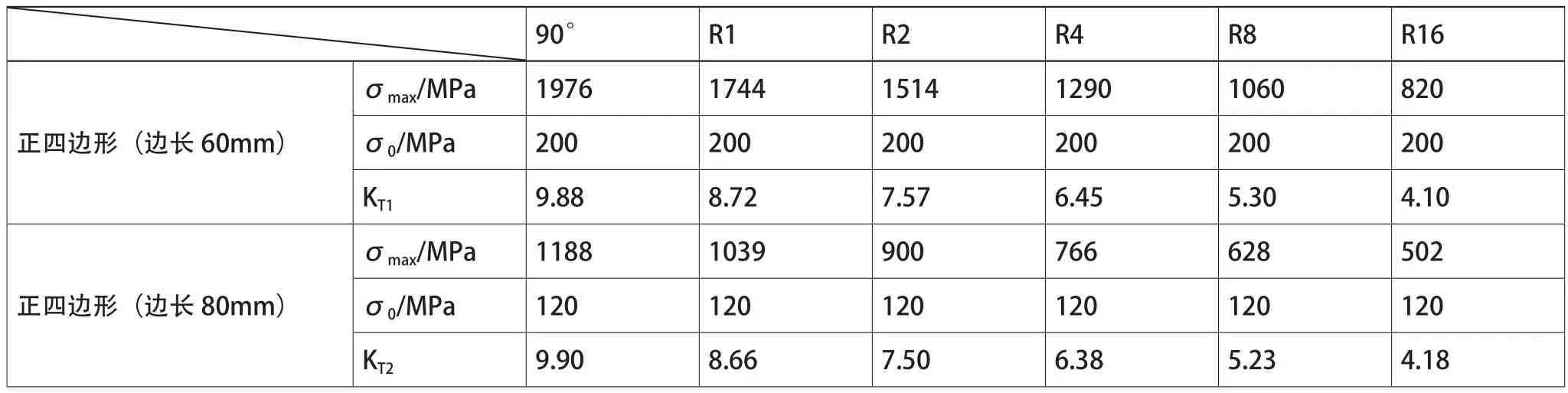
表2 理论应力集中系数
⑶函数拟合。
在上文分析的基础上,将圆角半径值R作为自变量,将对应的KT值作为因变量,通过数据处理,拟合二者的函数关系。由于拐角处为90°时以及R20和R40时是模具拐角圆角变化的两种极值情况,前者是R值极小,通过模拟结果,其KT值已在表2给出;后者是R值极大,此时模具型腔是一个圆形,不存在应力集中情况,其KT值视为1。对于这两种极值情况,只是作为参考,拟合时只考虑R1,R2,R4,R8和R16,以KT1作为拟合对象,拟合结果如公式2所示。
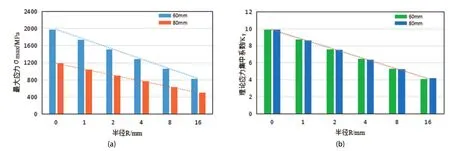
图7 KT对比图
拟合公式2表明,模具拐角的应力集中程度(KT)与圆角半径值的对数(lnR)呈线性关系,将拟合数据和试验数据对比,结果如图8所示。
由图8可以看出,拟合函数与试验数据基本重合,并且其变化趋势与图7(b)试验结果一致,说明拟合函数是成功的,通过拟合函数不仅能很好的表达圆角半径变化对模具应力集中程度的影响规律,而且能达到定量研究的目的。

图8 拟合函数与试验数据对比
结论
⑴创新性地在冷挤压模具应力集中研究中引入了理论应力集中系数(KT),提出以KT为基础,通过函数拟合,将冷挤压模具应力集中程度的研究定量化,试验结果及分析表明,该方案是可行的。
⑵以正四边形型腔模具为例,影响模具型腔拐角应力集中程度(KT)的决定因素是拐角处过渡圆角半径值(R),而与模具边长无关。通过拟合得到KT与R的函数关系:

通过与试验数据对比,该函数拟合是成功的,能很好的表达圆角半径变化对模具应力集中程度的影响规律,达到定量研究的目的。
