由一道题的多种解法引出对一类题型的通法研究

江苏省淮阴中学(223002)

卢连伟●



由一道题的多种解法引出对一类题型的通法研究

江苏省淮阴中学(223002)

卢连伟●

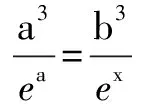
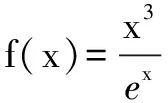
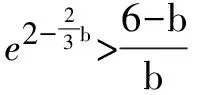
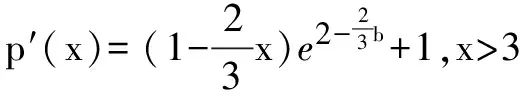
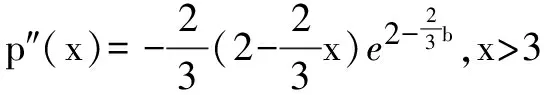
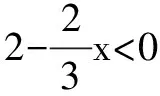
∴F(x)在(0,3)单调递增，(3，+∞)单调递减.

∴03.要证a+b>6只要证b>6-a>3,

即证F(b)>F(6-a).∵F(a)=F(b)，即证F(a)

令P(x)=F(x)-F(6-x),0

即证3(t+1)lnt<6(t-1),t∈(0,1).

令p(t)=3(t+1)lnt-6(t-1),t∈(0,1),

∴p′(t)在(0，1)单调递减，∴p′(t)

∴p(t)在(0，1)单调递减，∴p(t)

题后反思 上述方法中的前两种方法的本质实际上是一样的，都是把零点通过单调性偏移到极值的同一侧，便于构造函数证明，只不过第一种方法是直接偏移，第二种方法是通过取对数后再偏移，第三种方法是构造零点比值作为新的变量.这两类方法对于这种零点不等式问题的证明非常有效，希望读者深刻体会.

牛刀小试 设函数f(x)=ex-ax,a为常数.(1)求f(x)的单调区间；(2)若函数f(x)有两个相异零点x1、x2，求证x1+x2>2.

分析 (1)f′(x)=ex-a.①a≤0时，f′(x)>0,∴f(x)在(-∞,+∞)单调递增；②a>0时，f(x)在(-∞,lna)单调递减，(lna,+∞)单调递增.(2)∵f(x)在(-∞,lna)单调递减，(lna,+∞)单调递增,

∴fmin(x)=f(lna)=a-alna<0,∴lna>1,∴a>e.

方法一 由f(x1)=ex1-ax1=0及f(x2)=ex2-ax2=0,

G632

B

1008-0333(2017)13-0048-01