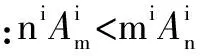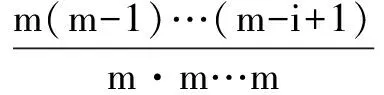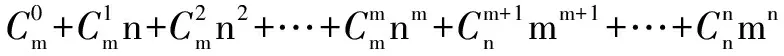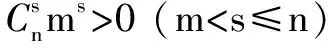巧用二项式定理证明不等式

贵州省盘县十二中(553539)

阮世雄●



巧用二项式定理证明不等式

贵州省盘县十二中(553539)

阮世雄●

二项式定理是高中数学中很重要的一部分内容，它的应用范围非常广泛，用法非常灵活.证明与n(n∈N)次方有关的不等式是其重要用途之一，这里略举几例供大家参考.

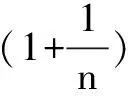
证明 应用二项式定理(注意这里n≥2)，结合放缩法有

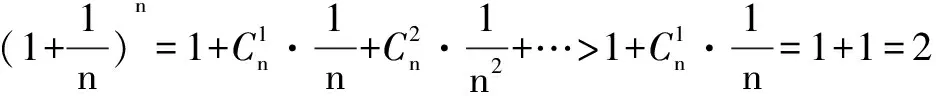
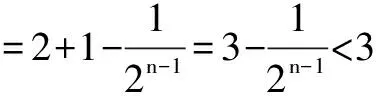
反思 先利用二项式定理把乘方式展开，再恰当使用放缩法，是解决这类问题的常用思路.

例2 已知n∈N，n≥2，求证3n>(n+2)·2n-1.

分析 本题不如上题的结构明朗，似乎与二项式定理的形式有很大的出入.我们可以把3n进行变形构造出定理的形式，注意到不等式右边含有2n-1，因此可以考虑把3n变形为3n=(2+1)n.

证明 在条件n∈N，n≥2下：

即有3n>(n+2)·2n-1(n∈N，n≥2).

反思 本题的关键是构造出符合二项式定理的形式，这是我们应用二项式定理证明不等式的主要技巧.

例3 已知n∈N，n≥1，求证：(2n+1)n≥(2n)n+(2n-1)n.

分析 本题的证明思路很容易寻找，我们先把所要证的式子简单变形为(2n+1)n-(2n-1)n≥(2n)n，再运用二项式定理把左边两项展开即可.

证明 ∵(2n+1)n-(2n-1)n

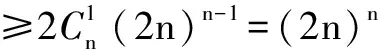
∴(2n+1)n≥(2n)n+(2n-1)n(n∈N，n≥1).

反思 对于(1+x)n±(1-x)n的计算应该注意符号上的规律.

例4 已知i、m、n是正整数，且1

分析 问题(1)用排列数公式即可解决；问题(2)应该建立在问题(1)的基础上，再借助二项式定理进行解决.

只要证ni·m(m-1)…(m-i+1)

由二项式定理可知：

反思 这一道试题，综合考查了排列数公式、组合数公式及二项式定理等知识，有一定的难度.很多同学在平时的学习中只注意了二项式定理的其他应用，忽视了证明不等式这一方面的训练，造成了严重失分.

G632

B

1008-0333(2017)13-0009-01