偏序集上的局部极大滤子

王逸芬，卢涛（淮北师范大学 数学科学学院，安徽 淮北 235000）

偏序集上的局部极大滤子

王逸芬，卢涛
（淮北师范大学 数学科学学院，安徽 淮北 235000）

在偏序集上引入局部极大滤子的概念，讨论局部极大滤子在格、分配格、Heyting代数、Boole代数中的相关性质，得到一些等价条件，进一步地丰富偏序集的内容.

偏序集；极大滤子；局部极大滤子

0 引言

滤子作为偏序集上的一个特殊的集合，同时也具有很多好的性质，对滤子的研究也一直没有间断过.本文受文献［1-2］启发，引入偏序集上的局部极大滤子的概念，并在格、分配格、Heyting代数、Boole代数中讨论其相关性质.

1 偏序集上局部极大滤子的概念

定义1［3］设L为偏序集，L的任意余定向上集成为L的滤子.L的全体滤子记作FIL(L)对于L的滤子F，若0∉F，则称F为真滤子.

定义2 设L为偏序集，M是其上的真滤子，若存在某元素x∈LM，使得M在不含x的所有的滤子中极大（x∉F⊇M蕴涵着F=M），那么称M是L的关于元素x的极大滤子，简称偏序集上的局部极大滤子.

注1 偏序集上的极大滤子都是局部极大滤子，但是反之不一定成立.

例1 如图1所示，在偏序集L中，{a,c,1}，{b,c,1}是L的极大滤子，且它们分别是关于点b和a的极大滤子，然而{1}是L关于c点的极大滤子，不是极大滤子，且{c,1}不仅不是极大滤子，同时也不是局部极大滤子.

注2 例1不仅说明极大滤子类是局部极大滤子类的真子类；也说明局部极大滤子是滤子类的真子类.

引理1 对偏序集L上的真滤子F，∀x∈LF，则必存在关于元素x的极大滤子M，使得x∉M⊇F.

证明 记P={ℑ:ℑ是L的真滤子且x∉ℑ⊇F}.由条件知，F⊆P，故P≠ϕ，并且P是关于集合包含关系⊆的一个偏序集，显然P中任意链均有上界，故根据Zorn引理知，P中必有极大元，该极大元就是关于元素x的极大滤子M.

引理2 设F是格L的真滤子，且x∈LF，令F1=⋂{↓(x∧a):a∈F}，则F1是滤子，且F1⊂F.

证明 任取b1,b2∈F1，那么分别存在a1,a2∈F，使得b1≤x∧a1,b2≤x∧a2，从而有b1∧b2≤(x∧a1) ∧(x∧a2)=x∧(a1∧a2)，也就是b1∧b2∈↓(x∧(a1∧a2)).由于F是滤子，a1∧a2∈F，从而有b1∧b2∈F1，即F1余定向.又因为F1是上集，故F1是L的滤子，且F1⊆F.又x∈F1,x∉F，故F1⊂F.

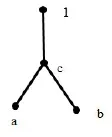
图1 偏序集上的局部极大滤子不是极大滤子

引理3 设F是格L的真滤子，且x∈LF，那么F是L关于元素x的极大滤子当且仅当∀y∈LF，存在a∈F，使y∧a≤x.

证明 必要性.设F是L关于元素x的极大滤子，对任意y∈LF，令F1=⋂{↓(y∧a):a∈F}，由引理2，F1是滤子，且F1⊂F.又由F的极大性，x∈F1，那么存在a∈F，使y∧a≤x.

充分性.由x∈LF，根据引理1，存在关于元素x的极大滤子M，使得x∉M⊇F.下证M=F.假设M≠F，从而根据条件，存在a∈F，使得y∧a≤x.又M⊇F，故a∈M，又M是滤子从而y∧a∈M，根据M是上集知，x∈M，这与x∉M相矛盾，故M=F，即F是L关于元素x的极大滤子.

推论1 设F是L关于元素x的极大滤子，那么有∀y∈F,a∈F，则必有y∧a≰x.

证明 假设y∧a≤x，由y∈F,a∈F以及F是理想，知y∧a∈F，而F是上集，于是x∈F，这与x∉F矛盾，故y∧a≰x.

2 偏序集上局部极大滤子的相关性质

定理1 格L上的局部极大滤子全是不可约滤子.

证明 设M是一个L关于元素x的极大滤子，x∉M，若假设存在滤子F和H，使M=F⋂H，且F⊃M,H⊃M，则存在a∈F,a∉M，b∈H,b∉M.又由引理3知，分别存在c,d∈M，使a∧c≤x,b∧d≤x，由F⊃M,H⊃M,从而有c∈F,d∈H.又因为a∈F,b∈H,故a∧c∈F,b∧d∈H,从而有x∈F,x∈H，于是x∈F⋂H，即x∈M，然而这与x∉M相矛盾，故M是不可约滤子.

注3 极大滤子都是不可约滤子，但反之不一定成立.

例2 如图2所示，在格L中，F={a,b,c,1}是不可约滤子，但是不存在元素x∈LF，使得F是L关于元素x的极大滤子，从而F不是局部极大滤子.

推论2 格中的极大滤子全都是不可约滤子.

推论3 分配格中的局部极大滤子全都是素滤子.

注4 1）以上推论说明，在分配格中的局部极大滤子都是素滤子，但反之不一定成立.如在图2中的L是分配格，F={a,b,c,1}是素滤子，但F不是L的局部极大滤子.

2）在格L中局部极大滤子是介于极大滤子和不可约滤子之间的一种类滤子.

定理2 设L是半格，F是L的真滤子，且LF是有限集，则下列条件中

1）F是滤子；

2）sup(LF)∉F；

3）F是L的局部极大滤子.必有1）⇒2）⇒3）成立.

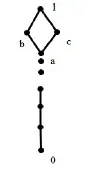
图2 偏序集上的不可约滤子不是局部极大滤子

2）⇒3）.令t=sup(LF)，因t∉F，由引理1，存在关于t的极大滤子M，使得t∉M⊇F.下证M=F.假设M≠F，则存在x∈M,x∉F，又t=sup(LF)，故x≤t，而x∈M，M是上集，故t∈M，而这与t∉M相矛盾，故M=F，因此F是L的局部极大滤子.

推论4 设L是分配格，F是L的真滤子，且LF是有限集，则下列条件等价

1）F是滤子；

2）sup(LF)∉F；

3）F是L的局部极大滤子.

定义2［4］设L是格，若对任意的a,b∈L存在对任意的c∈L，有c≤(a→b)⇔c∧a≤b，则称L是Heyting代数.

定义3［4］设L是含有最小元0的Heyting代数，a∈L，记¬a=a→0=∨{x∈L:a∧x=0}，则称¬a是a的伪补或否定，特别，¬0=1,¬1=0.

定理3 设L是含有最大元1的Heyting代数，F是L的真滤子，x是L中任意元素，在下列条件中

1）F是L的局部极大滤子；

2）F是L的素滤子；

3）对任意x∈L，x和¬x至少有一个在F中，而¬x和¬¬x有且只有一个在F中.则有1）⇒2）⇒3）成立.

证明 1）⇒2）.设F是L的局部极大滤子，由L是Heyting代数，L是分配格，再由推论3知，F是L的素滤子.

2）⇒3）.设F是L的素滤子，对任意x∈L，由于x∨¬x=1∈F以及F是L的素滤子，则x和¬x至少有一个在F中.由¬¬x∨¬x=1∈F及F是L的素滤子知，¬¬x和¬x至少有一个在F中，又由L是含有最大元1的Heyting代数知，¬¬¬x=¬x，从而¬¬x和¬x互为补元，即¬¬x∧¬x=0.由于F是L的真滤子，0∉F，故¬¬x与¬x是不可能同时存在F中的，从而¬x和¬¬x有且只有一个在F中.

注5 1）在定理3中3）⇒1）是显然不成立的，如图3所示，令F={c,1}，则1∈F，¬1=0∉F，¬¬1=1∈F；c∈F，¬c=1∈F，¬¬c=0∉F，满足条件3），然而F不是L的局部极大滤子，同时也不是L的素滤子.

2）例2中，L也是Heyting代数，F={a,b,c,1}是素滤子，易看出F却不是L的局部极大滤子.

推论5 设L是包含最大元1的Heyting代数，F是L的滤子，x∈L，若¬x与¬¬x有且只有一个在F中，F是L的真滤子.

证明 由¬¬1=1∈F，而¬x和¬¬x有且只有一个在F中，故¬1=0∉F，从而F是L的真滤子.

命题1［4］设L是包含最大元1的Heyting代数，则有L是Boole代数当且仅当∀x∈F,¬¬x=x.

定理4 设L是Boole代数，x是L中任意元素，则下列条件等价：

1）F是L的素滤子；

2）任意x∈L，x与x′有且只有一个在F中；

3）F是L的极大滤子；

4）F是L的局部极大滤子.

证明 1）⇒2） 由于L是Boole代数可知，∀x∈F,¬¬x=x，且¬¬x与¬x互为补元，从而¬x=x′，再根据定理3可证.

2）⇒3） 根据1∈F，可知0=1′∉F，那么F是L的真滤子，设H是L的滤子，若有F⊆H,F≠H，则必存在x∈H,x∉F，由条件，x′∈F⊆H，从而x′∈H，F=H，所以F是L的局部极大滤子.

3）⇒4） 根据注1得证.

4）⇒1） 设F是L的一个局部极大滤子，由L是Boole代数，易知L是分配格，又由推论3能够推出F是L的素滤子.

注6 若L是Boole代数，则局部极大滤子、素滤子等价.

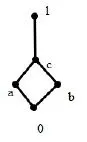
图3 Heyting代数中的真滤子F={c,1}不是局部极大滤子

［1］姜广浩，徐罗山.偏序集上的滤子极大理想［J］.模糊系统与数学，2007，21（4）：35-42.

［2］肖璨，姜广浩，杨慧.偏序集上的理想极大滤子及其应用［J］.吉林师范大学学报（自然科学版），2013，34（1）：13-15.

［3］郑崇友，樊磊，崔宏斌.Frame与连续格［M］.北京：首都师范大学出版社，2000：44-74.

［4］GIERZ G，HOFMANN K H，KEIMEL K，et al.Continuous lattices and domains［M］.Oxford:Cambridge University Press，2003：89-97.

Locally Maximal Filters on Posets

WANG Yifen，LU Tao
（School of Mathematical Sciences，Huaibei Normal University，235000，Huaibei，Anhui，China）

In this paper，the definition of the locally maximal filters on posets are given，and discuss some properties in lattices，distributive lattices，Heyting algebra，Boolean algebra，and get some equivalent proposi⁃tions，to further enrich the content of posets.

poset；maximal filters；locally maximal filters

O 153.1

A

2095-0691（2017）02-0006-03

2016-10-17

国家自然科学基金项目（11171156）；安徽省高校自然科学研究重点项目（KJ2015A064）

王逸芬（1990— ），女，安徽淮北人，硕士生，研究方向：格上拓扑学.

卢 涛（1974— ），男，山东诸城人，博士，教授，研究方向：拓扑学，范畴论.