振荡水柱式波能转换系统气室压强理论研究
2017-06-05杜小振赵继强朱文斗曾庆良
杜小振, 赵继强, 张 燕, 朱文斗,曾庆良
(山东科技大学机械电子工程学院, 山东 青岛 266590)
振荡水柱式波能转换系统气室压强理论研究
杜小振, 赵继强, 张 燕, 朱文斗,曾庆良
(山东科技大学机械电子工程学院, 山东 青岛 266590)
振荡水柱式波能发电系统中波能转换主要结构气室能将入射波能转换为往复振荡的空气动能从而实现能量一次转换,该过程的气室压强研究对发电系统设计具有重要意义。因此针对“引浪板”和“引浪通道”的三维侧向开口固定式振荡水柱波能转换系统,采用三维Green函数法建立了气室内水气动力学性能的压缩空气压强理论计算模型。计算时为了满足压强与速度连续条件,响应脉动源与扰动脉动源两者在交界面上需要相互匹配;同时为了能够精确快速地求解三维Green函数,采用了多维切比雪夫(Chebyshev)多项式和渐近展开式快速近似计算方法。计算结果表明所用方法简单可靠,同时计算结果可应用于振荡水柱波能发电系统性能预测及相关问题研究。
振荡水柱;气室;波浪能;压缩空气压强
振荡水柱式(Oscillation Water Column,OWC)波能发电是目前研究和应用较广的波能发电方式之一,具有转换效率高、结构简单、造价低等特点。徐勤勤等[1]研究了二维引浪板结构的侧向开口固定式波能转换装置的水动力性能,并优化了引浪板倾角,结果表明加装“引浪板”后,提高了气室转换效率。梁贤光等[2]利用造波水槽模拟实验研究了汕尾100 kW波力电站气室模型的性能,实验结果表明气室波能转换效率与波周期、波高和气室形状有关。刘瑧[3]构建了基于水气两相 VOF 模型的三维数值波浪水槽,采用物理模型试验方法研究了气室内相对压强与入射波要素的关系。纪君娜等[4]采用计算流体力学Fluent软件构建三维数值波浪水槽研究气室前的波浪传播与气室内振荡水面变化规律。耿楠[5]通过调整OWC腔室内振荡压强幅值和相位,使其工作于消反射状态,提高波能吸收效率。
以上研究侧重试验建模分析,本文将采用三维Green函数法建立数学理论模型,分析振荡水柱式波能转换系统水气动力性能。用时域Green函数法直接求解水动力学问题时,需要对Green函数及其导数作卷积,同时由于被积函数的振荡和增幅特性,计算繁杂、困难、精度低。因此对三维无限水深Green函数,Newman[6]、Beck与Liapis[7]提出级数算法,Ferrent[8]、Magee与Beck[9]、黄德波[10]提出造表插值算法,Clement[11]提出了分方程算法;对三维有限水深Green函数,Clement与Mas[12-13]也提出函数级数算法,却未计算导数值;Newman[14]与Teng等[15]使用了 Chebyshev多项式分区域逼近三维有限水深Green函数的算法,计算量较大;戴愚志等[16]通过分析有限水深Green函数在不同区域的渐近特性,采用了多维 Chebyshev多项式和渐近展开式计算有限水深Green函数及其导数的方法, 并且可以计算源点和场点的任意距离。
本文采用三维Green函数法计算振荡水柱式波能转换系统结构如图1所示,箱体总高度h1=120 mm,吃水深度h4=10 mm,底角曲率半径r1=10 mm。箱体侧向开口上缘与倾斜迎浪板相连,引浪板高度h3=75 mm,选取其与垂直面夹角为α=30°时,同时它与箱体侧面及底板延伸部分形成200 mm的引浪通道L2,将有利于增加装置波能吸收效率。开口高度h2=35 mm,箱体内部自由水面上部为正方形气室,气室长L1=100 mm,其内自由水面(如图1中阴影部分)在波浪作用下作升降往复振荡运动并压缩气室内空气形成动力。
1 振荡水柱式波能转换系统理论计算
振荡水柱式波能发电系统中能量一次转换过程为入射波带动气室内水柱做升降振荡,进而带动水体上部空气通过输气管与外界大气之间做往复运动,空气驱动透平电机转动便可实现波浪能向电能转换,称为能量二次转换过程。能量从一次转换到二次转换过程中气室是其主要结构,气室内压强可以反映该发电系统工作性能的优劣。因此首先研究水柱振荡方程,其次研究箱体内振荡水柱流体动力特性,最后研究OWC波能转换系统气室压强。
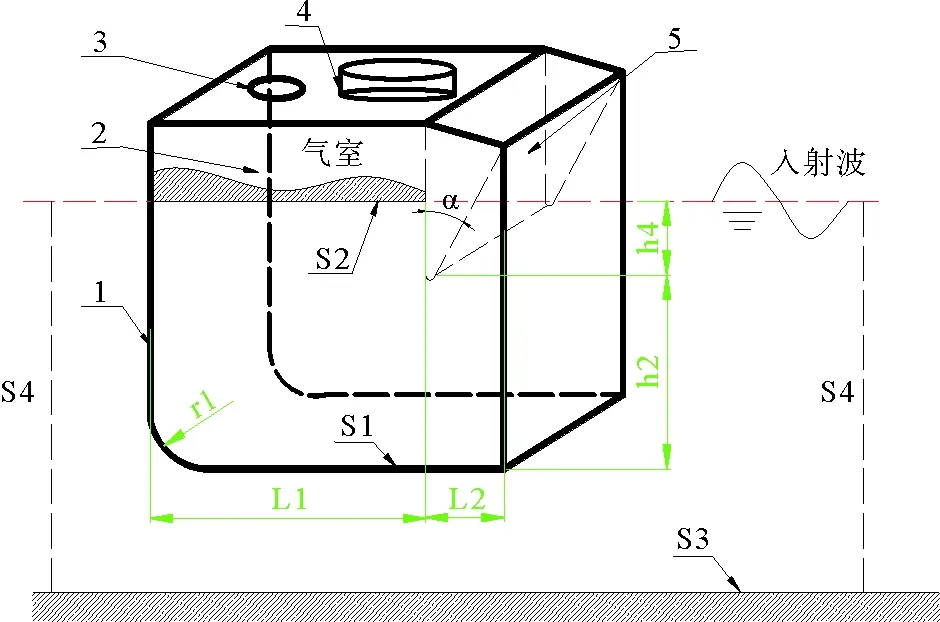
(1.振荡水柱式箱体;2.气室;3.旁路节流阀;4.输气管道;5.引浪板。 1.Box of oscillating water column;2.Air chamber;3.Bypass throttle; 4.Gas pipeline;5.Wave board.)图1 振荡水柱式波能转换系统示意图Fig.1 Wave energy conversion system with oscillating water column
1.1 波能转换系统振荡水柱运动方程

(1)
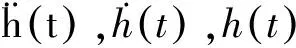
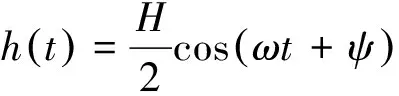
(2)
式中:H为振荡水柱的内波高全幅值;ψ为气室内水面振动初相位。
1.2 箱体内振荡水柱流体动力特性
波浪与物体相互作用的流体动力学问题关键是求解流场中的速度势,即求解在确定的边界条件下的Laplace方程。目前已有许多成熟的方法可以求解Laplace方程边值问题,本文利用Green函数法求解流场速度势。因此需要首先定义Laplace方程的边界条件,其次利用Green函数法求解流场速度势。
1.2.1 Laplace方程的边界条件 如图1所示假设箱体表面为S(x,y,z)=0的三维半潜体,其流体边界由水底S3z=-h,自由表面z=0、箱体瞬时表面S1及无穷远处S4组成,假定流体均匀、不可压缩、无黏性、运动无旋,忽略表面张力,则流场内速度势Φ可以定义为[17]:
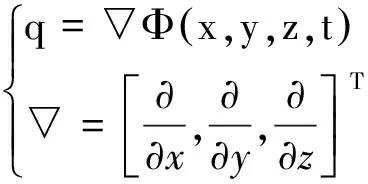
(3)
式中:q为流体的速度矢量,在微幅运动情况下;Φ可表示为:

(4)
将连续性方程▽Tq=0代入(3)可得到Laplace方程:
▽2φ=0,
(5)
规则波浪的线性边界条件通过摄动展开求得:
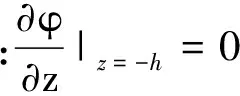
(6)
箱体瞬时表面条件:

(7)
vn表示箱体表面上法向速度分量值,由式(8)给出:

(8)
箱体内部表面无压力自由液面条件:根据运动学和动力学关系给出线性复合边界条件:

(9)
表面复压力Pm的线性复合边界条件为[18]:

(10)
式(10)中:复压力Pm由下式定义:
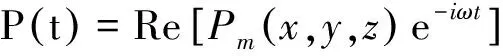
(11)
辐射条件:
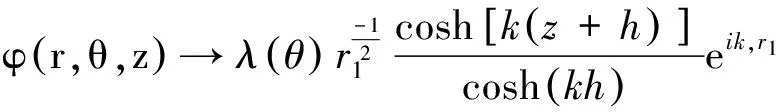
(12)

前述(5)、(6)、(7)式组成了初、边值问题的定解条件,根据此条件,用三维Green函数法求解流场速度势时,需要将形成振荡水柱的箱体分为两个区域,即箱体内区域和箱体外区域,同时也要注意衔接内域和外域以满足压力与速度连续条件,因此需讨论以下3个区域问题。
1.2.2 内域问题 假定流体运动无旋、不可压缩,运动从t =0时开始,在有限时间t内,根据线性叠加原理,规则线性波流场内速度势是入射势Φi和绕射势Φs的线性叠加[19]:
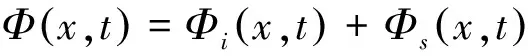
(13)
式中:x位移向量;t时间变量。
对于有限水深中单一频率、单一方向的入射波,入射势Φi为已知条件,可用式(14)计算。

(14)
式中:h水深;k入射波的波数;β入射波浪的方向角。
ΦS表示波高为H1的入射波所引起的物体绕射速度势,可由Green函数法根据定解条件求解[20]:
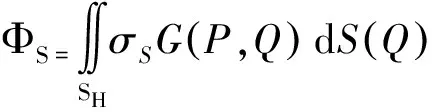
(15)
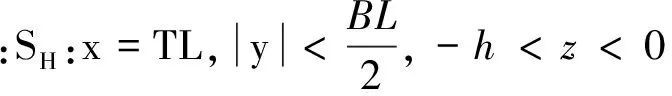
▽2Φ=0 在Ω1域内,

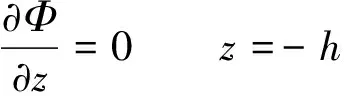
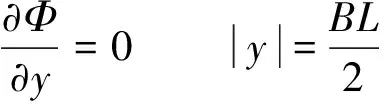
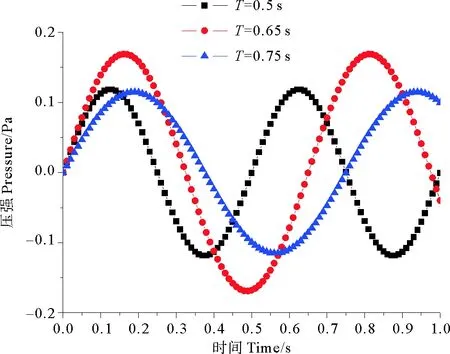
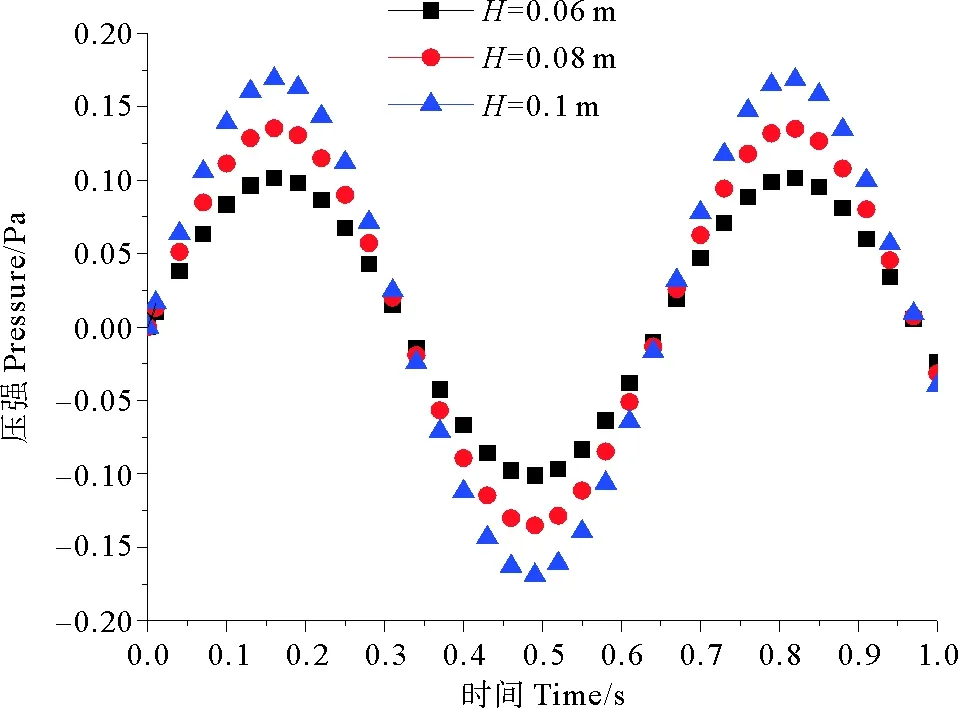
1.2.3 外域问题 与内域问题相似,可建立外域Ω2(Ω2:x>TL,-h ▽2Φ1=0 在Ω2域内, 1.2.4 内外域的衔接问题 在内外域衔接面的内、外侧,即箱体的开口处,应满足流体速度与压力的连续条件,以保证内外域的匹配,内外域衔接条件为: (16) Φi+Φs=Φ1, (17) 1.3 时域内有限水深Green函数求解流场速度势 1.3.1Green函数表达式以及精确快速解法Wehausen和Laitone[21]以三维脉动源的形式给出了满足边界条件的Green函数为 (18) (19) (20) (21) 综上所述Green函数可以表示为: (22) 其中: (23)为了迅速求解F0,需要避免无穷积分,采用如下变形(1)当X>1时,使用Fourier级数可以将F0表示为 (24) 式中K0为修正汉克尔函数。 (2)当0≤X≤1,采用Chebyshev多项式逼近F0,系数bmn如下表, 。 (25) (26) (27) (28) F∞为无穷水深中的Green函数,已有较为成熟的计算方法[11],虽然F-F∞不存在奇点,但是格林函数及其上述导数数值积分本身具有振荡、收敛缓慢、耗费大量计算时间等特点。而Chbeyshve多项式具有精度高、收敛速度快和可以避免缓慢的直接数值积分,故采用Chebyshev展开式计算。Chebyshev多项式是在区间[-1,1]上逼近其它函数的一种重要工具,对于给定的x值,可计算f(x)近似值如下[22]: (29) (30) 式中:cj为Chebyshev展开式的系数;ani为Chebyshev多项式系数。 利用Chebyshev将F-F∞展开式为: (31) (32) 式中Chebyshev多项式系数矩阵[a]的各元素定义见Abramowitz&Stegun[23]。 1.3.2 源强σs的解法 上述1.3.1节内容可以计算出Green函数,为了求解绕射速度势即公式(15),需要三维脉动源布置在箱体表面和衔接面上,其源强σs由第二类Fredholm方程及满足边界条件用离散化数值方法[24]求解: (33) 气室压强按正弦规律变化,并与箱体内水面升降振荡速度成正比。当入射势Φi和绕射势Φs确定以后,根据公式(13)就可以求出流场内总速度势Φ,之后对Φ求关于时间导数可以得到气室内压缩空气压强计算公式为 (34) 其中:μ为气室内空气升降振荡有效阻尼系数[25]。 刘瑧[3]选用物理模型为长30m,宽0.6m,高0.8m的波浪水槽,海况为气室宽度6.0m,前墙吃水2.5m,前墙厚度1.0m,入射波浪波幅0.5m,波浪周期为5.5s,实验结果得到三维气室压强为幅值为0.6pa的正弦曲线;刘月琴[26]选用一个气室宽度3m,长度6m的全反射无限长的直立式海岸上的波能转换装置,海况为波浪入射角0°,周期T=2.02s,试验得到气室压强曲线为幅值为0.05Pa的正弦曲线。因此本文通过理论模型如图1所示,分别计算分析比较了气室压强随波浪周期、浪高和水深变化的时程曲线,取入射波波长2.0m,方向角为0°,气室内水面振动初相位0°,水深0.1m,场点P(1,2,1),源强Q(4,6,2),图2为在水深0.1m分别比较了周期为0.5,0.65,0.75s的压强曲线,图3为在周期0.65s分别比较了浪高为0.06、0.08、0.1m的压强曲线,图4为在周期0.65s分别比较了水深0.1和0.15m的压强曲线,曲线如下: 由图2知,气室内压强呈正弦曲线变化规律随周期先增大后减小,最大压强幅值为0.169Pa,由图3知,压强与浪高成正比关系,在以上波浪及海况条件下气室内形成最大压强幅值为0.169Pa,由图4知,压强与水深成正比关系,在以上波浪及海况条件下气室内形成最大压强幅值为0.254Pa。 图2 压强随周期变化曲线Fig.2 The air pressure with the wave periodic 图3 压强随浪高变化曲线Fig.3 The air pressure with the wave height 图4 压强随水深变化曲线Fig.4 The air pressure with the water depth 本文采用三维Green函数法研究了安装有“引浪板”和“引浪通道”的三维侧向开口固定式振荡水柱式波能转换系统内形成的气室压强与各种波浪参数的关系。(1)比较本文通过理论计算分析获得的结果与刘瑧[3]刘月琴[26]等通过试验得到的结果,不仅气室压强变化规律相一致,而且能够满足振荡水柱气室内水气动力学特性;(2)在求解气室往复气流压强方法上与Lee[27]和Brito-Melo[28]相比,Lee和Brito-Melo在改变边界条件的情况下采用压力辐射法,本文首先利用三维Green函数法建立了气室内水气动力学性能的压缩空气压强理论计算模型,计算时采用多维Chebyshev多项式和渐近展开式快速近似计算方法可以精确快速求解三维Green函数,其次根据离散化方法求解出三维脉动源源强和上一步求出的三维Green函数就可以求得绕射势,最后对流场内总速度势求关于时间导数可以得到气室内压缩空气压强值,两者相比,本文计算过程简单;(3)根据给定的波浪与气室条件,计算结果表明气室内压强在周期0.65s、浪高0.1m时最大,此时气室具有最佳的水气动力性能。本文计算分析过程可用于振荡水柱波能发电系统性能预测及相关问题研究。 [1] 徐勤勤, 费乃振. 加有‘引浪板’的固定式气动型波能转换装置水动力性能的计算[J]. 上海交通大学学报, 1987, 21(5): 13-25.XuQQ,FeiNZ.CalculationofHydrodynamicPerformanceofFixedPneumaticWaveEnergyConverterwithaleadingwaveplate[J].JournalofShanghaiJiaoTongUniversity, 1987, 21(5): 13-25. [2] 梁贤光, 孙培亚, 游亚戈. 汕尾100kW波力电站气室模型性能试验[J]. 海洋工程, 2003, 21(1): 113-116.LiangXG,SunPY,YouYG.PerformanceexperimentofShanwei100kWwavepowerstationair-room[J].OceanEngineering, 2003, 21(1): 113-116. [3] 刘瑧. 岸式振荡水柱波能发电装置的试验与数值模拟研究[D]. 青岛: 中国海洋大学, 2008.LiuZ.ExperimentalandNumericalInvestigationofOscillatingWaterColumnWaveEnergyConverter[D].Qingdao:OceanUniversityofChina, 2008. [4] 纪君娜, 刘瑧, 纪立强. 振荡水柱波能发电装置气室的三维数值模拟研究[J]. 海岸工程, 2011, 30(2): 7-13.JiJN,LiuZ,JiLQ. 3DNumericalSimulationforOscillatingWaterColumnChamberinWave-powerConvertor[J].CoastalEngineering, 2011, 30(2): 7-13. [5] 耿楠. 振荡水柱波能转换器效率分析及改进方案研究[D]. 长沙: 湖南大学, 2012.GengN.EfficiencyAnalysisofOscillatingWaterColumnWaveEnergyConverterandtheModifiedDesign[D].Changsha:HunanUniversity, 2012. [6]NewmanJN.Theevaluationoffree-surfaceGreenfunctions[C].Washington:onNumericalShipHydrodynamics, 1985. [7]BeckRF,LiapisS.Transientmotionsoffloatingbodiesatzeroforwardspeed[J].JournalofShipResearch, 1987, 31(3): 164- 176. [8]FerrentPA.Fastcomputationalmethodfortransient3Dwave-bodyinteraction[C].Venice:ComputerModelingOceanEngineering, 1988. [9]MageeAR,BeckRF.VectorizedcomputationofthetimedomainGreenfunction[C].UK:WorkshoponWaterWavesandFloatingBodies, 1989. [10] 黄德波. 时域Green函数及其导数的数值计算[J]. 中国造船, 1992, 4: 16-25.HuangDB.Approximationoftime-domainfreesurfacefunctionanditsspatialderivatives[J].ShipBuildingofChina, 1992, 4: 16-25. [11]ClementAH.AnordinarydifferentialequationfortheGreenfunctionoftimedomainfreesurfacehydrodynamic[J].JournalofEngineeringMathematics, 1998(33): 201-217. [12]ClementA,MasS.Computationofthefinitedepthtime-domainGreenfunctioninthesmalltimerange[C].Japan:WorkshoponWaterWavesandFloatingBodiesKyushu, 1994. [13]MasS,ClementA.ComputationofthefinitedepthtimedomainGreenfunctioninthelargetimerange[C].UK:WorkshoponWaterWavesandFloatingBodies, 1995. [14]NewmanJN.Theapproximationoffree-surfaceGreenfunctions[C].London:WaveAsymptoticProceedingofFritzUrsellRetirementMeeting, 1990. [15]TengB,HanL,GouY.Fastevaluationoftime-domainGreenfunctionforfinitewaterdepth[J].ChinaOceanEngineering2003, 17(3): 417-426. [16] 戴愚志, 余建星, 郭海涛. 时域有限水深格林函数及其导数的数值计算[J]. 船舶力学, 2006, 9(5): 16-25.DaiYZ,YuJX,GuoHT.Approximationoftime-domainGreenfunctionforfinitewaterdepthanditsderivatives[J].JournalofShipMechanics, 2006, 9(5): 16-25 [17] 刘应中, 缪国平. 船舶与海洋工程水动力学导论[D]. 上海: 上海交通大学, 1983.LiuYZ,MiaoGP.AnintroductiontoshipandOceanEngineeringhydrodynamics[D].Shanghai:ShanghaiJiaoTongUniversity, 1983. [18] 梅强中. 水波动力学[M]. 北京: 科学出版社, 1984: 89-102.MeiQZ,Wavedynamics[M].Beijing:SciencePress, 1984: 89- 102. [19] 韩凌. 应用时域格林函数方法模拟有限水深中波浪对结构物的作用[D]. 大连: 大连理工大学, 2005.HanL.NumericalSimulationofWaveActiononStructuresUsingtheTime-DomainGreenFunction[D].Dalian:DalianUniversityofTechnology, 2005. [20]WangDJ,KatoryMY,LiS.Analyticalandexperimentalinvestigationonthehydrodynamicperformanceofonshorewave-powerdevices[J].OceanEngineering, 2002, 29: 871-885. [21]WehausenJV,LaitoneEV.SurfaceWaves[M].Berlin:HandbunchPhysikSpringerVerlag, 1960: 78-84. [22]WilliamHP.NumericalRecipes[M].UK:CambridgeUniversityPress, 1986: 67-83. [23]AbramowitzM,StegunIA.HandbookofMathematicalFunctionswithFormulas,Graphs,andMathematicalTables[M].NewYork:GovernmentPrintingOffice,WashingtonDC,DoverPublications, 1964. [24] 李远林, 张健, 陈加菁. 振动水柱港池系统的三维理论方法[J]. 华南理工大学学报(自然科学版), 1989, 17(4): 86-98.LiYL,ZhangJ,ChenJJ.A3DTheoreticaltechniqueofOWCwithAHarborsystem[J].JournalofSouthChinaUniversityofTechnology(NaturalSciences), 1989, 17(4): 86-98. [25] 吴雄健. 波浪能转换浮标的试验研究[C]. 上海: 上海交大交流论文, 1982.WuJX.Experimentalstudyofwaveenergyconversionbuoy[C].Shanghai:ExchangePapersofShanghaiJiaoTongUniversity, 1982. [26] 刘月琴, 武强. 岸式波力发电装置水动力性能试验研究[J]. 海洋工程, 2002, 20(4): 93-97.LiuYQ,WuQ.Experimentinvestigationonthehydrodynamicperformanceofshorelinewave-powerdevices[J].OceanEngineering, 2002, 20(4): 93-97. [27]LeeCH,NewmanJN,NielsenFG.Waveinteractionswithanoscillatingwatercolumn[J].InternationalSocietyofOffshoreandPolarEngineers, 1996, 1: 82-90. [28]Brito-MeloA,SarmentoAJNA.ClementAH,DelhommeauG.A3DboundaryelementcodeforanalysisofOWCwave-powerplants[J].InternationalSocietyofOffshoreandPolarEngineers, 1999, 1: 188-195. 责任编辑 陈呈超 Theoretical Research on the Air Pressure in Oscillation Water ColumnChamber for the Wave Energy Conversion System DU Xiao-Zhen, ZHAO Ji-Qiang, ZHANG Yan, ZHU Wen-Dou, ZENG Qing-Liang (College of Mechanical and Electronic Engineering, Shandong University of Science and Technology, Qingdao 266590, China) The wave energy conversion into electricity has been increasingly studied in the last years.The oscillating water column (OWC) is probably the most highly developed type of wave energy converter.The problem of the pressure control of an OWC in random waves was dealt with in this paper with theory analysis. In order to achieve the initial ocean wave energy conversion, the air chamber plays a critical role to translate incident wave energy into the bi-directional kinematic energy of air for the OWC wave energy generation. It is the pivotal factor to analyze the air chamber’s pressure. The three-dimensional fixed OWC wave power model are designed with a side entrance and associated with ‘leading wave plate’ and ‘leading wave channel’. The theoretical calculation method for the compressed air pressure in chamber is calculated by the three-dimensional Green function. In this analysis procedure the response oscillating source should match with the exiting oscillating source on a interface to meet with the continuous conditions between pressure and velocity. The multi-dimensional Chebyshev polynomials and asymptotic expansions was introduced to get the solution of the three-dimensional Green function quickly and accurately. The calculation program is simple and reliable to predict the hydrodynamic and aerodynamic performance especially the air pressure for the OWC wave energy generation systems. oscillation water column; air chamber; wave energy; the compressed air pressure 国家自然科学基金项目(51105234);中国博士后科学基金项目(2015M582113);山东省自然科学基金项目(ZR2016EEM23)资助 Supported by Chinese National Natural Science Foundation(51105234); China postdoctoral Science Foundation (2015M582113); Shandong Province Natural Foundation (ZR2016EEM23) 2015-03-16; 2016-03-15 杜小振(1978-),男,副教授,主要研究方向为海洋能发电、微电源、压电传感器技术等。E-mail:du_xzh@163.com TV7 A 1672-5174(2017)07-135-07 10.16441/j.cnki.hdxb.20150074 杜小振, 赵继强, 张燕, 等. 振荡水柱式波能转换系统气室压强理论研究[J]. 中国海洋大学学报(自然科学版), 2017, 47(7):135-141. DU Xiao-Zhen, ZHAO Ji-Qiang, ZHANG Yan, et al. Theoretical research on the air pressure in Oscllatron Water Column chamber for the wave energy conversion system [J]. Periodical of Ocean University of China, 2017, 47(7):135-141.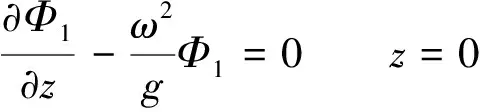
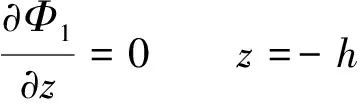
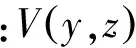
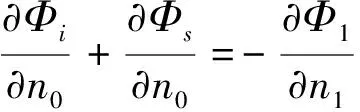



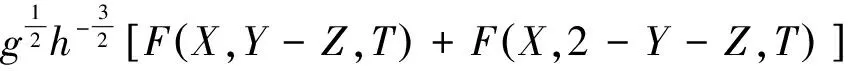
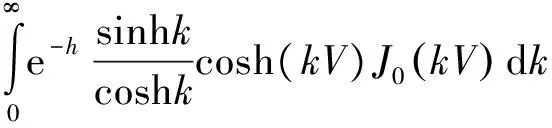
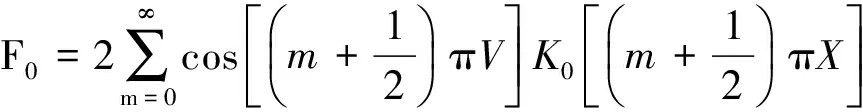
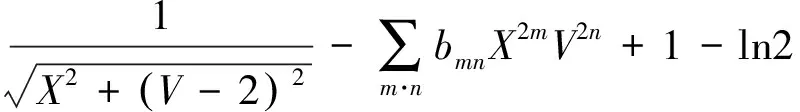
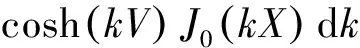
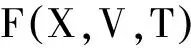
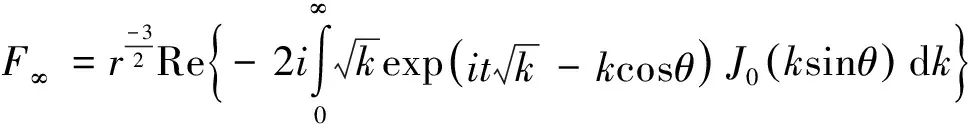
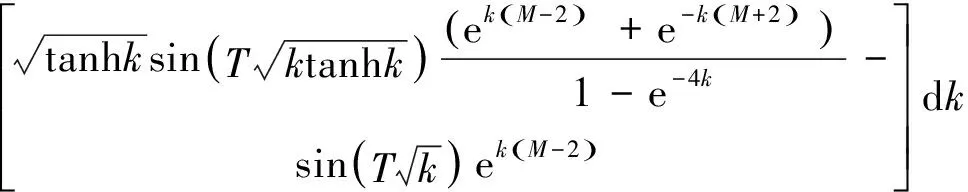
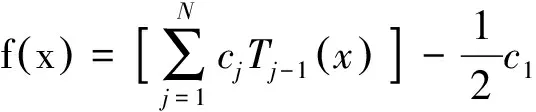
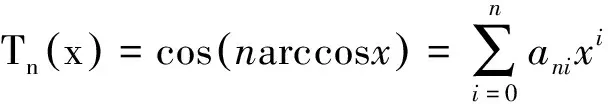

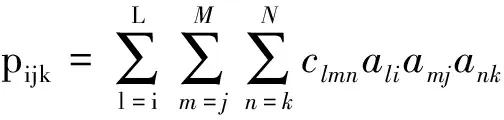

2 OWC波能转换系统气室压强
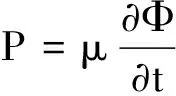
3 数值计算结果讨论

4 结论
