基于归一化局部互相关算法的相位编码全波形反演❋

夏冬明， 宋 鹏 ❋❋， 谭 军， 李金山， 张晓波， 钟梦轩

(1.中国海洋大学海洋地球科学学院，山东 青岛 266100；2.青岛国家海洋科学与技术实验室，山东 青岛 266100；3.海底科学与探测技术教育部重点实验室，山东 青岛 266100)

基于归一化局部互相关算法的相位编码全波形反演❋

夏冬明1,2,3， 宋 鹏1,2,3 ❋❋， 谭 军1,2,3， 李金山1,2,3， 张晓波1， 钟梦轩1

(1.中国海洋大学海洋地球科学学院，山东 青岛 266100；2.青岛国家海洋科学与技术实验室，山东 青岛 266100；3.海底科学与探测技术教育部重点实验室，山东 青岛 266100)

本文提出了一种基于归一化局部互相关算法的相位编码全波形反演方法，该方法细化了每个时窗内各模拟道与实际记录道的相关度，使得残差记录能更精确地反映速度模型扰动对于波场的影响，因此其适应于单边观测地震数据的相位编码全波形反演。模型实验表明：相比于归一化全局互相关算法，归一化局部互相关算法可更有效压制单边观测地震数据残差记录中的观测残差，并且基于归一化局部互相关算法的相位编码全波形反演的反演精度明显优于基于归一化全局互相关算法的相位编码全波形反演，其有望在实际数据的全波形反演中发挥重要作用。

全波形反演； 相位编码； 互相关

二十世纪八十年代，Tarantola等人首先基于最小平方理论提出了时间域全波形反演方法[1-2]，该方法充分利用实测地震记录的走时、振幅以及相位等信息来重建地下介质的速度结构，理论上对于理想观测系统其精度可达到波长数量级，因此全波形反演被认为是能够进一步提升地震勘探的油气勘探能力的重要方法，有望在未来的油气勘探中发挥重要作用。

经过几十年来的发展，时间域全波形反演方法在理论上和应用上都取得了长足的进步，但超大的计算量阻碍了其在实际生产中的应用。为了提高时间域全波形反演的计算效率，2009年，Krebs提出了基于相位编码技术的全波形反演方法[3]，其利用相位编码技术将所有炮合成一个超级炮集，仅应用一个超级炮集进行反演计算，大大提高了时间域全波形反演的计算效率。在2011和2012年的SEG年会上DiaZ和Ha分别提出了随机炮采样[4]和循环炮采样[5]全波形反演策略，DiaZ和Ha的测试结果显示，基于随机炮采样或循环炮采样策略的时间域全波形反演其计算效率一般可提高4～5倍，但仍不足以彻底解决时间域全波形反演的低计算效率问题。此外，近年来诸多学者开始尝试借助于GPU加速以提高全波形反演的计算效率，Wang等[6]和Mao等[7]的实验结果均显示基于GPU的全波形反演的计算效率一般可提高几十倍，但基于GPU的加速对硬件资源提出了更高的要求，也在一定程度上提高了计算成本。

相对而言，应用相位编码技术进行全波形反演(以下简称相位编码全波形反演)是目前提升全波形反演计算效率的最为经济有效的手段，但相位编码全波形反演更适应于全排列观测系统(即炮移动而接收道不动的采集方式)，而对于海上常规拖缆式单边观测地震数据，相位编码全波形反演会受到因观测系统差异导致的残差(以下简称观测残差)的影响而变得不收敛或降低反演精度。鉴于此，近年来Routh等、Choi等通过修改反演目标函数，提出并实现了基于归一化全局互相关法算法的相位编码全波形反演[8-10]，大大提高了海上单边观测地震数据的相位编码的稳定性和反演精度。Routh、Choi等提出的基于全局互相关算法的相位编码全波形反演是通过应用归一化全局互相关算法求取出每一道的模拟记录和实际记录互相关值，并以此计算得到相位编码全波形反演的残差记录，其可在一定程度上弱化观测残差，但应用归一化全局互相关算法求取的各道每个采样点的互相关值均相同，其忽视了各道不同时窗的信息差异，导致参与反演计算的残差记录中依然存在部分观测残差，降低了反演的精度。

本文提出并实现了一种基于归一化局部互相关算法的相位编码全波形反演(以下简称归一化局部互相关相位编码全波形反演)，其可细化各模拟道与实际记录道浅中深层的相关度，使得残差记录能更精确地反映因速度模型扰动产生的波场变化，从而显著提高海上单边观测地震数据相位编码全波形反演的精度。

1 相位编码时间域全波形反演原理及其实现流程

1.1 相位编码时间域全波形反演原理

时间域全波形反演方法可归纳为求取一个最优化的速度模型c，使得目标函数E(p(c),c)最小，其中：

(1)

式中：Ns为总炮数；sn为第n炮的震源子波；dn为第n炮的观测记录；p(c,sn)表示基于速度模型c，以sn为震源的合成地震记录，其满足声波方程：

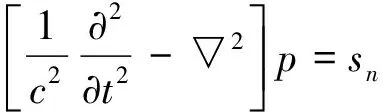
(2)

(1)式表明，常规时间域全波形反演其计算量与地震数据的炮数成正比，计算效率极其低下。为提高时间域全波形反演的计算效率，2009年，Krebs提出了相位编码全波形反演方法[3]，其将(1)式改写为：

(3)

这里⊗表示褶积，en是随机生成的编码函数序列，Krebs指出，当en为随机生成的+1或-1时[3]，炮间的串扰可得到有效地压制，因此本文的en也取为随机生成的+1或-1。

由于p(c,sn)是震源的线性函数，因此式(3)可写为[3]：

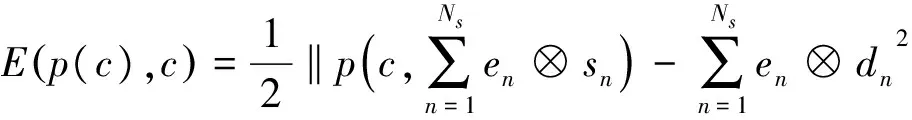
(4)

当应用式(4)进行全波形反演时，先将每一炮的震源褶积上一个随机相位编码函数，所有炮合成一个超级震源，并应用相同的编码函数对观测地震记录进行褶积，从而得到一个超级记录，然后应用该超级震源和超级记录进行反演计算，将多震源子波与多炮的反演计算转换为一个超级震源与一个超级记录的反演，因此相位编码全波形反演计算效率可提高约炮数倍。

1.2 相位编码时间域全波形反演实现流程

与常规时间域全波形反演类似，相位编码全波形反演通常也需基于梯度类的迭代寻优来实现，其具体实现步骤为：

①给定初始模型和震源子波，并将震源子波分别褶积上一个随机的编码函数序列生成超级震源，同时将对应的炮分别褶积上相同的编码函数序列得到观测的超级炮集记录。

②基于给定的初始模型和超级震源进行正演模拟计算，得到正时波场u(x,t)(这里x表示空间坐标，t表示时间)和模拟的超级炮集记录，并计算得到目标函数。

③以观测的超级炮集记录和模拟的超级炮集记录之差(残差记录)作为逆时扰动，计算得到逆时波场ψ(x,t)，并按下式计算得出梯度值：

(5)

式中：d表示梯度；c(x)表示速度模型；上标“.”表示时间的一阶微分；T表示最大时间。

④基于线搜索理论[11]计算得到迭代步长，然后根据梯度和迭代步长修改模型，即完成本次迭代。

⑤重复①～④，直到目标函数满足要求或达到最大迭代次数(相位编码全波形反演具体反演流程见图1)。

图1 相位编码全波形反演流程Fig.1 The flow chart of the time-domain phase-encoded FWI

2 基于归一化局部互相关的相位编码全波形反演

由于在基于超级震源进行正演模拟时只能采用双边全排列接收方式，因此相位编码全波形反演理论上仅适合于基于双边全排列观测系统的地震数据，而对于海上单边观测系统数据的相位编码全波形反演，其残差记录中会存在大量观测残差，这种观测残差会严重影响全波形反演的稳定性和反演精度。鉴于此，Routh、Choi等提出了一种基于归一化全局互相关算法的相位编码全波形反演[8-10]，其将目标函数修改为[10]：

(6)

此时，波场的残差记录定义为[10]：

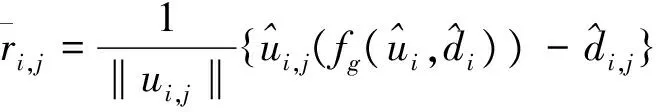
(7)

其中：

(8)

即fg为归一化的模拟超级记录和实际超级记录的零延迟互相关值。

由于引入了各道的互相关值，因此基于(7)式计算得到的残差记录大大弱化了观测残差，从而可有效提高单边观测系统地震数据相位编码全波形反演的稳定性和精度。但全局互相关算法在计算残差记录时，每一道只有一个互相关值，这样做忽视了每一道不同时窗的信息差异，使得残差记录中依然存在部分观测残差，鉴于此，本文提出了一种基于归一化局部互相关算法的残差记录计算方法，波场的残差记录定义为：

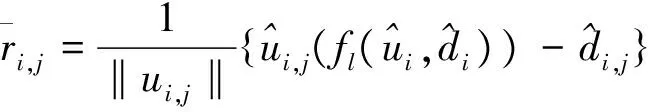
(9)

其中：

(10)

即fl为归一化局部互相关。该方法在引入滑动时窗的基础上计算每一道每一个采样点的互相关值，细化了每个时窗内各个模拟道与实际记录道的相关度，使得残差记录能更精确地反映速度模型扰动产生的波场变化，从而可有效提升单边观测系统地震数据的反演稳定性和精度。

设记录长度为TN，取时窗长度为TW，每一道每个采样点的归一化局部互相关值可按以下步骤计算：

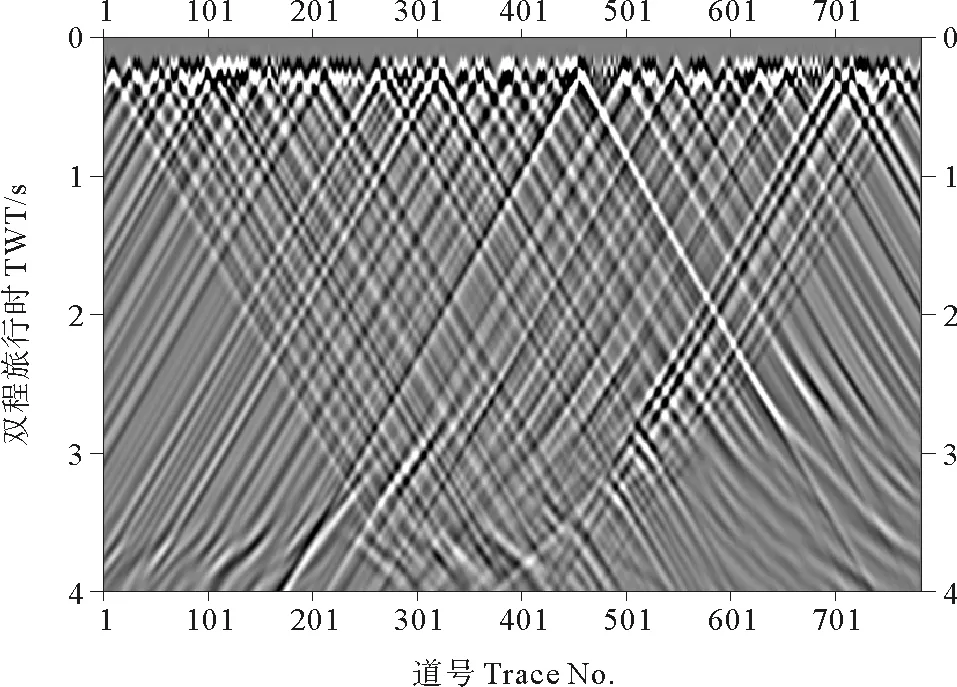
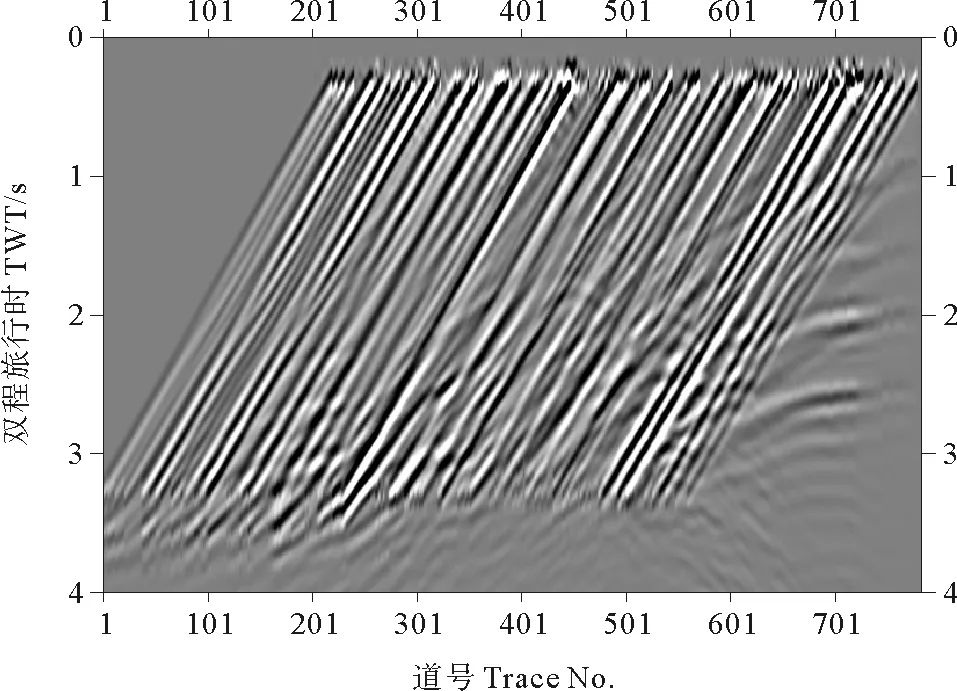
①在第一个TW时窗内，基于式(10)计算出归一化的模拟超级记录和实际超级记录的零延迟互相关fl(t)，并将其作为时窗中心点TW/2的互相关值，对于t

②将时窗向下滑动一个采样点，并重复①操作，从而得到第二个时窗的中心点的零延迟互相关值。

③随着时窗不断向下滑动，最终可得到TW/2～(TN-TW/2)范围内所有点的互相关值。

④对于t>TN-TW/2的时间采样点，令fl(t)=fl·(TN-TW/2)，这样即可得到该道每个采样点的模拟记录和实际记录间的互相关函数值。

归一化局部互相关算法的时窗长度TW是一个重要的参数，若TW太大，其难以起到细化各个模拟道与实际记录道的相关度的作用，导致残差记录求取的精度不高(当TW为整个记录长度时，局部互相关算法退化为全局互相关算法)，而若TW太小，又容易导致反演不稳定。大量的实验表明：当TW取200～300 ms时效果最佳，本文的数值实验中归一化局部互相关算法的时窗长度TW取为240 ms。

对每一道都进行归一化局部互相关值求取，即可得到模拟超级地震记录和观测超级地震记录每一道每一个采样点的归一化局部互相关值，在此基础上可根据式(9)和式(6)分别计算出残差记录和目标函数，然后即可进行相位编码全波形反演处理。除残差记录和目标函数求取的差异外，归一化局部互相关相位编码全波形反演与常规相位编码时间域全波形反演的处理流程完全相同，这里不再赘述。

3 模型反演效果分析

本文采用扩展的Marmousi速度模型进行反演实验。扩展的Marmousi模型是在Marmousi速度模型[12]的基础上左边扩展4.5 km，右边扩展2 km，扩展出部分的速度值与原始模型的左右边界值相同(扩展Marmousi模型如图2所示，这里仅显示模型4.5 ～13.7 km区域，以下同)。

图2 Marmousi速度模型Fig.2 The Marmousi velocity model

基于该扩展的Marmousi模型，采用右边放炮、左边接收的单边观测方式，模拟得到共561炮地震记录(第200炮地震记录如图3所示)作为反演的观测地震记录。该炮集记录每炮为220道接收，最小偏移距为120 m，炮间隔和道间隔均为20 m，炮点深度和接收点深度也均为20 m。

图3 第200炮地震记录Fig.3 The 200th shot record

对真实模型进行平滑处理，并以此作为反演的初始模型进行相位编码全波形反演实验(初始模型如图4所示)。为降低相位编码全波形反演的串扰影响，每次迭代时本文采用随机炮分组方式都将所有炮分为四组进行相位编码全波形反演计算，不失一般性，这里仅基于第一组的超级炮集记录及其残差记录进行分析。

图4 初始速度模型Fig.4 The original velocity model

由观测地震记录计算得到的超级炮集记录如图5所示，基于超级震源模拟得到的模拟超级地震记录见图6，常规相位编码全波形反演的残差记录见图7，基于归一化全局互相关算法和归一化局部互相关算法的相位编码全波形反演的残差记录分别见图8和图9。

由图5和图6可知，由于观测炮集记录采用单边观测系统，因而由其经相位编码技术得到的超级炮集记录仅由左边接收的观测数据形成，而基于超级震源模拟得到的超级记录中却包含了左右两边接收的地震数据，因此常规相位编码全波形反演的残差记录中包含

图5 实际记录的相位编码超级炮集Fig.5 The phase-encoded super-record of seismic records

图6 模拟的超级记录Fig.6 The modelled super-record

图7 传统全波形反演的残差记录Fig.7 The residual record of conventional FWI

了大量观测残差(图7中箭头所示)。相对而言，归一化全局互相关相位编码全波形反演其残差记录已经大大弱化观测残差，但其依然可见部分残余(图8中箭头所示)；而对比图8和图9可知，归一化局部互相关相位编码全波形反演其残差记录中，观测残差的压制效果明显优于基于归一化全局互相关算法的相位编码全波形反演。

常规相位编码全波形反演、归一化全局互相关相位编码全波形反演以及归一化局部互相关相位编码全波形反演的140次迭代结果分别见图10、图11和图12。

图8 归一化全局互相关法的残差记录Fig.8 The residual record of normalized global correlation

图9 归一化局部互相关法的残差记录Fig.9 The residual record of normalized local correlation

对比图10、图11和图12可知，对于单边观测系统数据，常规相位编码全波形反演其整体反演效果不佳，尤其是深层精度较低；归一化全局互相关全波形反演的整体反演效果明显优于常规相位编码全波形反演，深层的高速体和下伏地层的反演精度得到较大改善，但仍与真实模型相差较大；归一化局部互相关全波形反演的整体反演精度最高，深层的高速体和下伏地层已经较为逼近真实模型，这充分显示了归一化局部互相关全波形反演方法对于单边观测地震数据的相位编码全波形反演的优势。

图10 常规相位编码全波形反演结果Fig.10 The result of conventional phase-encoded FWI

图11 归一化全局互相关相位编码全波形反演结果Fig.11 The result of normalized global cross- correlation phase-encoded FWI

图12 归一化局部互相关相位编码全波形反演结果Fig.12 The result of normalized local cross- correlation phase-encoded FWI

为进一步量化以上三种反演方法的整体反演精度，本文采用Ben-Hadj-Ali定义的一个反演精度评估因子来对以上反演结果进行评估，其表达式为[13]：

(11)

其中：mresult表示最终反演模型；mreal表示真实模型。根据(11)式计算得到的以上反演结果的精度评估因子Eres值详见表1。

表1 反演结果的Eres值

Note：①Conventional Phase Encoding；②Normalized Global Cross-correlation；③Normalized Local Cross-correlation

由表1可知，归一化局部互相关全波形反演方法的整体反演精度最高，其最接近于真实模型。

4 结论与展望

本文提出并实现了基于归一化局部互相关的相位编码全波形反演方法，理论分析和模型实验表明，对于单边观测系统地震数据的相位编码全波形反演，相比于归一化全局互相关算法，归一化局部互相关算法可更有效压制残差记录中的观测残差，显著提升单边观测系统地震数据相位编码全波形反演的精度，从而可有力推动相位编码全波形反演在实际数据中的应用，有效解决全波形反演的低计算效率问题。

当然，对于实际数据的全波形反演来讲，除计算效率低下外，实际数据中各种噪音、地震子波和初始模型的精度等对于全波形反演都有重要的影响。因此，深入分析噪音、地震子波和初始模型的精度等对于全波形反演的影响，并研究高精度的去噪、子波提取和初始模型建立方法和技术，以全面推动全波形反演在实际数据中的应用，将是下一步的研究工作。

[1] Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266.

[2] Tarantola A. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 1986, 51(10): 1893-1903.

[3] Jerome R， Krebs, John E.Anderson, David Hinkley, et al. Fast full-wavefield seismic inversion using encoded sources[J]. Geophysics, 2009, 74(6): 177-188.

[4] Diaz Esteban. Fast full waveform inversion with random shot decimation[C]. San Antonio: 81th Annual International Meeting, SEG, Expanded Abstracts, 2011: 2804-2808.

[5] Ha Wansoo， Shin Changsoo, Efficient full waveform inversion using a cyclic shot sampling method[C]. Las Vegas: 82th Annual International Meeting, SEG, Expanded Abstracts, 2012: 1-6.

[6] Wang Baoli, Jinghuai Gao. CUDA-base acceleration of full waveform inversion on GPU[C]. San Antonio: 81th Annual International Meeting, SEG, Expanded Abstracts, 2011: 2528-2533.

[7] Mao Jian, Wu Rushan, Wang Baoli. Multiscale full waveform inversion using GPU[C]. Las Vegas:82th Annual International Meeting, SEG, Expanded Abstracts, 2012:1-7.

[8] Routh Partha, Krebs Jerry Lazaratos Spyros. Encoded Simultaneous Source Full-Wavefield inversion for spectrally shaped marine streamer data[C]. San Antonio: 81th Annual International Meeting, SEG, Expanded Abstracts, 2011: 2433-2438.

[9] Routh P S, Krebs J R， Lazaratos S, et al. Full-wavefield inversion of marine streamer data with the encode simultaneous source method[C]. Vienna: 73th conference & Exhibition: EAGE, Extened Abstracts, 2011: 23-26.

[10] Choi Yunseok. and Alkhalifah Tariq, Application of multi-source waveform inversion to marine streamer data using the global correlation norm[J]. Geophysical Prospecting, 2012, 60(4): 748-758.

[11] Gauthier O, Virieux J, Tarantola A. Two-dimensional nonlinear inversion of seismic waveforms: Numerical results[J]. Geophysics, 1986, 51(7): 1387-1403

[12] Gray S H, May W P. Kirchhoff migration using eikonal equation traveltimes[J]. Geophysics, 1994, 59(5): 810-817.

[13] Ben-Hadj-Ali H, S Operto, J Vineux. An efficient frequency-domain full waveform inversion method using simultaneous encoded sources[J]. Geophysics, 2011, 76(76): 109-124.

责任编辑 徐 环

The Phase-Encoded Full Waveform Inversion Basedon Normalized Local Cross-Correlation Algorithm

XIA Dong-Ming1,2, 3, SONG Peng1,2,3, TAN Jun1,2, 3,LI Jin-Shan1,2, 3, ZHANG Xiao-Bo1, ZHONG Meng-Xuan1

(1. College of Marine Geo-Science, Ocean University of China, Qingdao 266100, China；2. Qingdao National Laboratory for Marine Science and Technology，Qingdao 266100，China；3. Key Lab of Submarine Geosciences and Prospecting Techniques Ministry of Education, Qingdao 266100, China)

In this paper, a method of phase-encoded full waveform inversion based on normalized local cross-correlation algorithm is proposed，which can discribe the correlation degree of modelled seismic traces and actual seismic traces in each time window, so the method is more suitable for the phase-encoded full waveform inversion of unilateral observation seismic data since the residual record can reflect the effect of velocity model perturbation on wave field accurately, Numerical experiments show that: the normalized local cross-correlation algorithm can more effectively suppress the observation residuals in the residual record of unilateral observation seismic data compared with the normalized global cross-correlation algorithm, and the inversion accuracy of full waveform inversion based on normalized local cross-correlation algorithm is obviously better than that of full waveform inversion based on normalized global cross-correlation algorithm, so it is expected to play an important role in waveform inversion of actual data.

full waveform inversion; phase-encoded; cross-correlation

国家自然科学基金项目(41574105)；国家重大科技专项(2016ZX05027-002)；青岛海洋科学与技术国家实验室鳌山科技创新计划项目(2015ASKJ03)资助 Supported by National Natural Science Fundation of China(41574105)；National Science and Technology Major Project(2016ZX05027-002)；The Scientific and Technology lnnovation Project Financially Supported by Qingdao National Laboratory for Marine Science and Technoloy(2015ASKJ03)

2016-03-30 ；

2016-05-16

夏冬明(1970-)，男，副教授，主要从事信号分析及反演方法研究。E-mail：dongmingx@163.com

❋❋ 通讯作者：E-mail：pengs@ouc.edu.cn

P631.4

A

1672-5174(2017)07-105-07

10.16441/j.cnki.hdxb.20160101

夏冬明，宋鹏，谭军,等.基于归一化局部互相关算法的相位编码全波形反演[J].中国海洋大学学报(自然科学版),2017, 47(7): 105-111.

XIA Dong-Ming, SONG Peng, TAN Jun,et al.The phase-encoded full waveform inversion based on normalized local cross-correlation algorithm[J].Periodical of Ocean University of China, 2017, 47(7): 105-111.