弹性介质Hamilton正则方程与地震波方程❋
2017-06-05栾锡武方建会
方 刚, 栾锡武, 张 斌, 方建会
(1.国土资源部油气资源和环境地质重点实验室,青岛海洋地质研究所,山东 青岛 266071;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东 青岛 266071;3.中国石油大学(华东)理学院,山东 青岛 266580)
弹性介质Hamilton正则方程与地震波方程❋
方 刚1,2, 栾锡武1,2, 张 斌3, 方建会3
(1.国土资源部油气资源和环境地质重点实验室,青岛海洋地质研究所,山东 青岛 266071;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东 青岛 266071;3.中国石油大学(华东)理学院,山东 青岛 266580)
地震勘探中地震波在地球介质内传播的过程非常复杂,而处理复杂系统问题时分析力学理论具有优越性。本文将地球介质看作是弹性介质,建立均匀和非均匀弹性介质的Hamilton正则方程,使弹性介质分析动力学方程由位形空间拓展到了相空间。利用弹性介质的Hamilton正则方程导出均匀与非均匀弹性介质的地震波方程和声波介质的地震波方程,为用Hamilton分析动力学研究地球介质中地震波传播、处理和解决地震勘探中的有关问题提供了基础。同时给出了用分析动力学理论处理解决地震勘探有关问题的思路。
地震勘探;分析力学;弹性介质;Hamilton正则方程;地震波方程
地震波方程刻画了地震波在地球介质中的传播规律,是地震波动力学理论的核心。研究地震波方程的建立、求解及其在地震勘探中的应用是地震波动力学的重要目标,以地震波动力学为基础,发展起来的地球物理勘探技术,例如波动方程的正演模拟技术、基于波动方程的反演技术、波动方程地震偏移技术等在油气等资源的地震勘探中有着广泛应用。因此,地震波方程在地震勘探理论、技术及应用研究中占有非常重要的地位。基于不同的理论和方法研究如何建立和求解各种介质的地震波方程,将有助于地震勘探理论、技术及应用的发展。
实际的地球介质结构比较复杂,表现出很强的非均质性,地震波场在其中的传播过程是非常复杂的。在处理复杂系统问题时分析力学理论更具优越性,特别是由于计算机技术的快速发展,分析力学理论和方法已经被越来越多地用于解决复杂工程对象中的动力学计算问题[1]。近十多年来,国内外分析力学研究者利用李群的无限小群变换和李代数研究拉格朗日(Lagrange)系统[2-5]、哈密顿(Hamilton)系统[6-9]、伯克霍夫(Birkhoff)系统[10-11]等,取得了许多重要的理论成果[12-19],然而,关于这些理论成果的应用研究还很不够,如何将这些理论成果应用于工程等实际问题是人们倡导研究的方向。笔者试图将这方面的理论成果应用于地震勘探领域的波场传播等问题的研究,以期望能够发展新的地震勘探方法,处理和解决地震勘探中的有关实际问题。
研究地震波场的传播问题,实质上就是研究波动方程的建立和求解问题。在实际应用中,当采用了无能量损耗的假设时,便可用弹性波动方程或标量波动方程来描述地震波传播。一切真实的物理过程、在耗散可忽略不计的情况下都可表示成Hamilton体系[20],如果在无能量损耗的条件下,用Hamilton体系描述地震波,弹性波动方程给出的地震波传播过程实质上为一个单参数的辛变换,系统在任意时刻状态由初始状态通过单参数辛变换群变换得到,其数值算法是辛几何算法。文献[21-22]研究了地震勘探中地震波传播的Hamilton表述、辛几何算法、共反射点轨迹等。文献[23]基于声格固体(PLS)方法研究了声波和弹性波传播的Hamilton系统方法模拟。本文将地球介质当作是弹性介质,引入弹性介质的Hamilton密度函数,建立均匀和非均匀弹性介质的Hamilton正则方程,将弹性介质分析动力学方程由位形空间拓展到相空间。利用弹性介质的Hamilton正则方程分别导出均匀与非均匀弹性介质和声波介质的地震波方程,为地震波方程Hamilton化,利用Hamilton分析动力学理论及其对称性与守恒量理论研究地震波传播、处理和解决地震勘探中的有关问题奠定基础。同时给出用分析动力学理论处理解决地震勘探有关问题的思路。
1 弹性介质的Hamilton方程
地震勘探中地球介质可被看作弹性介质,为用Hamilton分析力学理论和方法研究处理地震勘探中地震波传播等问题,现建立弹性介质的Hamilton方程。
对于弹性介质中的质点,设其位置矢量为
r=xi+yj+zk,
(1)
而位移矢量为
u=ui+vj+wk。
(2)
由于对介质中质点的位置,是在质点静止不动的状态下定义的,故质点的位置坐标x,y,z是不随时间t变化的,但质点的位移矢量是随时间t变化,而且处于不同位置的质点具有不同的位移,因此u是x,y,z和t的函数,即u=u(x,y,z,t)。
如果以ui(i=1,2,3,分别表示x,y,z)表示位移矢量u=u(x,y,z,t)的三个分量,即u1=ux=u,u2=uy=v,u3=uz=w。按照分析力学方法,选取广义坐标qs(s=1,2,…,n),这里的qs=qs(x,y,z,t),于是ui可表示为
ui=ui(qs,x,y,z,t) (i=1,2,3;s=1,…,n)。
(3)
式(3)中的x,y,z是与t等同的参量。
均匀弹性介质的Lagrange方程为[24]

(4)

对非均匀的弹性介质,则其Lagrange方程为[24]

(5)
其中:

(6)

(7)
为了得到弹性介质的Hamilton分析动力学方程,引进对应于广义坐标qs的广义动量密度
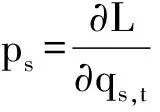
(8)
基于勒让德(Legendre)变换引入弹性介质的Hamilton密度函数
H=qs,tps-L。
(9)
这里要求从式(8)反解出qs,t,代入式(9)消去对qs,t的依存性。
由式(9)可得
dH=qs,tdps+psdqs,t-dL,
(10)
而

(11)
故

(12)
将方程(4)代入上式可得

(13)
考虑到H是qs,ps,qs,i,xν的函数,即H=H(qs,ps,qs,i,xν),则有

(14)
比较式(13)和式(14),有

(15)
和

(16)
利用式(8),式(15)可进一步写为

(17)
上式就是均匀弹性介质的Hamilton正则方程。
将方程(5)代入上式(12)得

(18)
比较式(18)和式(14),有
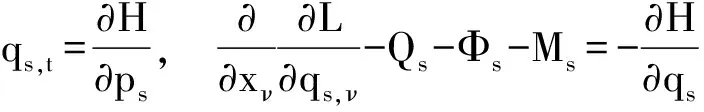
(19)
于是得非均匀弹性介质的Hamilton正则方程
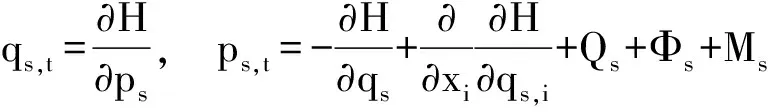
(20)
通常情况下一般都认为ρ,Cijkl只是空间位置的函数,即ρ=ρ(x,y,z),Cijkl=Cijkl(x,y,z),这时有Φs=0,Ms=0,由式(20)可知,在这种情况下非均匀弹性介质的Hamilton正则方程与均匀弹性介质的Hamilton正则方程具有相同的形式。
这里通过引入弹性介质的Hamilton密度函数,建立了弹性介质的Hamilton正则方程,将弹性介质分析动力学方程由位形空间拓展到了相空间。相空间的Hamilton正则方程与位形空间的Lagrange方程分别是2n个一阶微分方程组和n个二阶微分方程组,前者比后者简单,且有许多优越的性质。尽管两者是同一物理规律的不同数学表述,它们在物理上是相互等价的,但是它们在计算上是不等价的。将两者表示成数值算法时,它们的计算过程是不同的,在Hamilton体系表述下的算法是辛几何算法,在Lagrange体系表述下的算法是有限元方法,Hamilton正则方程具有辛结构,Hamilton表述下的辛几何算法具有高保真性。
2 弹性介质的地震波方程
地震波方程在地震勘探理论与技术研究中起着极为重要作用,下面利用弹性介质Hamilton正则方程建立弹性介质的地震波方程。
2.1 各向同性均匀弹性介质的地震波方程
对各向同性弹性介质,应变能密度为[25]

(21)
式中λ,μ为拉梅系数。则

(22)
取广义坐标q1=u,q2=v,q3=w,则


(23)
可以得到

(24)
对各向同性的均匀弹性介质,ρ,λ,μ均为常数,将H代入Hamilton正则方程(17),对s=1,即u分量有

(25)

(26)


(27)
同理,对s=2,3,即v,w分量有
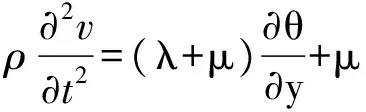
(28)

(29)
将式(27)(28)(29)合并,可得各向同性均匀弹性介质的地震波方程[24]

(30)
在不考虑波源的情况下,或者在波源以外的波场区,方程(30)可化为
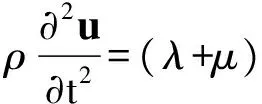
(31)
2.2 各向同性非均匀弹性介质的地震波方程
对各向同性的非均匀弹性介质,假设ρ,λ,μ,Cijkl是空间位置的函数,即ρ=ρ(x,y,z),λ=λ(x,y,z),μ=μ(x,y,z),Cijkl=Cijkl(x,y,z),将式(24)代入Hamilton正则方程(20),注意到广义坐标q1=u,q2=v,q3=w,则对s=1,即u分量有

(32)
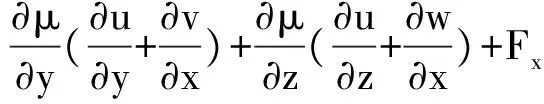
(33)
由式(32)(33)可以得到
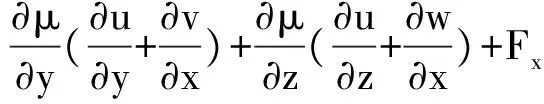
(34)
同理,对s=2,3,即v,w分量有
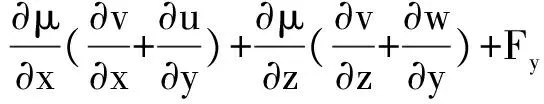
(35)

(36)
把式(34)(35)(36)合并,得各向同性非均匀弹性介质的地震波方程[24]


(37)
在不考虑波源的情况下,或者在波源以外的波场区,方程(30)可化为
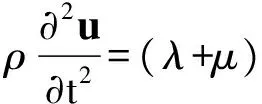

(38)
3 声波介质的地震波方程
实际地震勘探中,当弹性地震波场受采集因素限制难以获得时,常假设地下介质为声波介质,建立声波介质中的地震波方程是利用声波地震波场研究地下结构的基础。对于声波介质,μ=0,其Hamilton密度函数为

(39)
将式(39)代入Hamilton正则方程(20),对s=1,即u分量有

(40)

(41)
将式(40)代入式(41)可得

(42)
因声压
Pp=-λ▽·u
(43)
故有

(44)
同理,对s=2,3,即v,w分量有

(45)

(46)
将式(44)、(45)、(46)合并可得

(47)
由式(47)、(43)可得

(48)
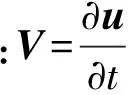
对密度ρ均匀的声波介质,由式(48)可得

(49)
其中f=▽·F。式(49)就是描述ρ均匀声波介质中地震波场的声波方程。在不考虑波源的情况下,或者在波源以外的波场区,方程(49)可化为

(50)
正则坐标和正则动量形成的相空间具有辛结构,一个力学或物理系统若能表示成Hamilton正则方程的形式,就会具有许多优越的性质。在上述3,4节中,基于相空间弹性介质Hamilton理论建立了弹性介质和声波介质的地震波方程,为在Hamilton体系下描述地震波,将地震波方程Hamilton化提供了基础。
4 结语
将地球介质视为弹性介质的情况下,利用分析力学方法,基于弹性介质的Lagrange方程,通过引入弹性介质的Hamilton密度函数,建立了均匀弹性介质和非均匀弹性介质的Hamilton正则方程,将弹性介质的分析动力学方程由位形空间拓展到了相空间;利用弹性介质的Hamilton正则方程导出了各向同性均匀和非均匀弹性介质地震波方程和声波介质地震波方程为应用Hamilton分析动力学理论及其对称性与守恒量理论研究地震波传播、处理和解决地震勘探中的有关问题奠定了基础。
分析力学理论在处理复杂系统问题时更具优越性,如果在Lagrange、Hamilton、Birkhoff等分析力学体系下描述地震勘探中的地震波,建立或导出各种类型地球介质的地震波方程,得到分析力学量与描述地震波的量之间的联系,则可利用分析力学的理论和方法研究地震波的传播、讨论各种介质中地震波的求解、处理和解决地震勘探中的有关问题:①在求解地震波方程时可利用分析力学积分理论与方法;②研究地震波传播的时间偏移时可利用Hamilton理论及其辛几何方法;③研究地震波场延拓深度偏移时可利用分析力学的群变换理论与方法;④研究地震波传播的保幅问题时可利用分析力学的对称性和守恒量理论与方法等。
[1] 刘延柱, 朱本华, 杨海兴.理论力学[M]. 北京: 高等教育出版社, 2009. Liu Y Z, Zhu B H, Yang H X. Theoretical Mechanics [M]. Beijing: Higher Education Press 2009.
[2] Tarasov V E, Zaslavsky G M. Nonholonomic constraints with fractional derivatives [J]. Journal of Physics A: Mathematical and General, 2006, 39(21): 9797-9815.
[3] Mei F X, Wu H B. Symmetry of Lagrangians of nonholonomic systems [J]. Physics Letters A, 2008, 372(13): 2141-2147.
[4] Fang J H, Zhang M J, Zhang W W. A new type of conserved quantity induced by symmetries of Lagrange system [J]. Physics Letters A, 2010, 374(17): 1806-1811.
[5] Nucci M C. Many conserved quantities induced by Lie symmetries of a Lagrangian system [J]. Physics Letters A, 2011, 375(11): 1375-1377.
[6] 罗绍凯. Hamilton系统的Mei对称性、Noether对称性和Lie对称性 [J]. 物理学报, 2003, 52(12): 2941-2944. Lou S K. Mei symmetry, Noether symmetry and Lie symmetry of Hamiltonian system [J]. Acta Phys Sin, 2003, 52(12): 2941-2944.
[7] Cai J L, Lou S K, Mei F X. Conformal invariance and conserved quantity of Hamilton systems [J]. Chin Phys B, 2008, 17(9): 3170-3174.
[8] Dorodnitsyn V, Kozlov R. Invariance and first integrals of continuous and discrete Hamiltonian equations[J]. Journal of Engineering Mathematics, 2010, 66(1): 253-270.
[9] Lou S K, Li L. Fractional generalized Hamiltonian equations and its integral invariants [J]. Nonlinear Dynamics, 2013, 73(1): 339-346.
[10] Chen X W, Zhang R C, Mei F X. Perturbation of symmetries of birkhoff system and adiabatic invariants[J]. Acta Mechanica Sinica, 2000 16(3): 282-288.
[11] Fu J L, Chen L Q. Perturbation of symmetries of rotational relativistic Birkhoffian systems and its inverse problem[J]. Physics Letters A, 2004, 324(2): 95-103.
[12] Agrawal O P. Generalized variational problems and Euler-Lagrange equations [J]. Comput Math Appl, 2010, 59(5): 1852-1864.
[13] 梅凤翔. 李群和李代数对约束力学系统的应用[M]. 北京: 科学出版社, 1999. Mei F X. Applications of Lie Groups and Lie Algebras to Constrained Mechanical Systems [M]. Beijing: Science Press, 1999.
[14] 梅凤翔. 约束力学系统的对称性与守恒量[M]. 北京: 北京理工大学出版社, 2004. Mei F X. Symmetries and Conserved Quantities of Constrained Mechanical Systems [M]. Beijing: Beijing Institute of Technology Press, 2004.
[15] 罗绍凯, 张永发. 约束系统动力学研究进展[M]. 北京: 科学出版社, 2008. Luo S K, Zhang Y F. Advances in the Study of Dynamics of Constrained System [M]. Beijing: Science Press, 2008.
[16] 张毅. 非保守动力学系统Noether对称性的摄动与绝热不变量[J]. 物理学报, 2013, 60(16): 164501. Zhang Y. Perturbation to Noether symmetries and adiabatic invariants for nonconservative dynamicsystems[J]. Acta Phys Sin, 2013, 62(16): 164501.
[17] 梅凤翔. 经典约束力学系统对称性与守恒量研究进展[J]. 力学进展, 2009, 39(1): 37-43. Mei F X. Advances in the symmetries and conserved quantities of classical constrained systems [J]. Advances in Mechanics, 2009, 39(1): 37-43.
[18] Jia L Q, Xie Y L, Zhang Y Y, Yang X F. A type of new conserved quantity deduced from Mei symmetry for Appell equations in a holonomic system with unilateral constraints[J]. Chin Phys B, 2010, 19(11): 110301-110306.
[19] Mei F X, Wu H B Two kinds of generalized gradient representationsfor holonomic mechanical systems[J]. Chin Phys B, 2016, 25(1): 014502.
[20] 冯康, 秦孟兆. 哈密顿系统的辛几何算法[M]. 杭州: 浙江科学技术出版社, 2003. Feng K, Qin M Z. Symplectic Geometric Algorithms for Hmiltonian Systems [M]. Hangzhou: Zhejiang Science and Technology Press, 2003: 185-205.
[21] 刘洪, 罗明秋, 李幼铭, 等. 共反射点轨迹的Hamilton方法[J]. 地球物理学报, 1999, 42(5): 685-694. Liu H, Lou M Q, Li Y M Yang KQ, et al. Hamilton method in describing common reflection point trajectory[J]. Chinese Journal of Geophysics, 1999, 42(5): 685-694.
[22] 罗明秋, 刘洪, 李幼铭. 地震波传播的哈密顿表述及辛几何算法[J]. 地球物理学报, 2001, 44(1): 120-128. Lou M Q, Liu H, Li Y M. Hamiltonian description and symplectic method of seismic wave propagation[J]. Chinese Journal of Geophysics, 2001, 44(1): 120-128.
[23] 曹禹, 杨孔庆. 对声波和弹性波传播模拟的Hamilton系统方法[J]. 物理学报, 2003, 52(8): 1984-1992. Cao Y, Yang K Q. Hamiltonian system approach for simulation of acoustic and elastic wave propagation[J]. Acta Phys Sin, 2003, 52(8): 1984-1992.
[24] 方刚, 张斌. 弹性介质的Lagrange动力学与地震波方程[J]. 物理学报, 2013, 62(15): 154502. Fang G, Zhang B. Lagrangian dynamics and seismic wave align of elastic medium [J]. Acta Phys Sin, 2013, 62(15): 154502.
[25] 朱滨. 弹性力学[M]. 合肥: 中国科学技术大学出版社, 2008. Zhu B. Elastic Mechanics [M]. Hefei: Press of University of Science and Technology of China, 2008.
责任编辑 徐 环
Hamiltonian Canonical Equations of Elastic Medium and Seismic Wave Equation
FANG Gang1,2, LUAN Xi-Wu1,2, ZHANG Bin3, FANG Jian-Hui3
(1.The Key Laboratory of Marine Hydrocarbon Resources and Environmental Geology, Ministry of Land and Resources, Qingdao Institute of Marine Geology, Qingdao 266071, China; 2.Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China; 3.School of Science in China University of Petroleum, Qingdao 266580, China)
The propagation of seismic wave in the earth medium is a complex process. The analytical mechanics theory has advantage to deal with complex systematic problems. In this paper, with the hypothesis of viewing earth medium as an elastic medium, the Hamiltonian dynamic equations are established for homogeneous and inhomogeneous elastic medium, which extends the analytic dynamics equations for elastic mediu from configuration space to phase space. Then the seismic wave equations of homogeneous and inhomogeneous elastic and acoustic medium are derived with the elastic Hamiltonian equations. These results provide theoretical basis for using Hamiltonian analytical mechanics theory to study seismic wave propagation and deal with the issuers in seismic exploration.
Seismic exploration; analytical mechanics; elastic medium; hamiltonian canonical equations; seismic wave equations
国家自然科学基金项目(41504109);山东省自然科学基金项目(BS2015HZ008)资助 Supported by the National Natural Science Foundation of China (41504109); the Natural Science Foundation of Shandong, China (BS2015HZ008)
2016-05-06;
2016-07-02
方 刚(1984-),男,博士,助理研究员。E-mail: fanggeo@163.com
O316,P632
A
1672-5174(2017)07-121-06
10.16441/j.cnki.hdxb.20160164
方刚, 栾锡武, 张斌, 等. 弹性介质Hamilton正则方程与地震波方程[J]. 中国海洋大学学报(自然科学版), 2017, 47(7): 121-126.
FANG Gang, LUAN Xi-Wu, ZHANG Bin, et al. Hamiltonian canonical equations of elastic medium and seismic wave equation[J]. Periodical of Ocean University of China, 2017, 47(7): 121-126.
