一种基于MMTD的决策树算法的研究∗

一种基于MMTD的决策树算法的研究∗

朱俚治

（南京航空航天大学信息中心南京210016）

决策树是一种常用的分类算法，自从ID3算法出现以来相关人员对该算法进行了不同程度的改进，由此出现了多种决策树算法。在决策树生成之时都采用递归算法来实现决策树结点的分裂，如果结点的信息增益越大，那么该结点被分裂的几率就越大。目前的ID3算法和C4.5算法中的信息增益成为结点是否被分裂的重要依据，因此根据决策树的结点进行分裂时信息增益所起作用的特点，论文提出了另外一种衡量信息增益大小的算法，该算法具有衡量公式以及核心算法——MMTD算法，论文的创新之处在于将MMTD算法在决策树中进行首次应用，并且在以MMTD为核心算法的基础之上，实现了对信息增益大小的衡量。

MMTD；决策树；信息熵；信息增益；ID3算法

Class NumberTP393

1 引言

在机器学习中决策树是一种分类算法，通过对样本的学习能够从学习中产生分类规则。决策树算法的优点是不需要大量的学习样本，通过有限的样本学习和训练就可以得出对数据分类时所需要的知识和规则。由于只需要有限的训练样本就能够建立一棵有效的决策树，因此决策树与其它算法相比较该算法具有较高的学习效率。

最早决策树算法是由Quinlan在1986年提出的，ID3算法对数据集分类的时候，取值只能是离散型数值，不能够对连续型属性值进行分类。为了改进ID3算法，在此基础之上出现了C4.5算法，该算法即可对离散型属性值进行分类同时又可以对连续型属性值进行分类。C4.5算法和ID3算法都是基于信息论的决策树算法，然而C4.5算法弥补ID3算法的不足之处，成为目前较为受欢迎的决策树算法［10～12］。尽管在ID3算法出现之后又出现众多的决策树算法，这些算法对ID3算法进行了改进工作，这些算法包括：CLS算法，CART算法，MBDT等算法。CLS算法的主要思想是首先构造一棵空的决策树，通过添加新的判断节点来完善原来的决策树，直到该决策树能够为训练实例正确分类为止［3～6］。而MBDT算法最大的优点是该算法与其它的算法相结合的情况下能够提高决策树算法分类时的效率［3～6，8］。以上的算法都是目前主要使用的决策树算法，也是流行的决策树算法。

在决策树算法生成过程中有两个重要步骤；第一步是创建决策树，第二步使用决策树对数据进行正确有效的分类。在决策树生成的过程中，最重要的是决定节点分裂的因素，在部分的决策树算法中采用信息论中的信息增益作为决策树结点分裂时的标准，如果决策树的某个结点的信息增益越大，那么该结点被分裂的可能性就越大。在ID3算法和C4.5算法之中都采用信息增益作为结点是否进行分裂的标准［10～12］。因此在本文中仍然采用信息增益率作为结点是否分裂的标准。

2 决策树技术简介

1）决策树的特点

决策树算法具体表现形式可以理解为是一棵树，决策树生成的时候从根结点开始以自顶向下的方式，采用递归算法不断地对结点进行分裂从而形成一棵完整的决策树。在决策树中有三种不同的结点：根结点，叶结点和内结点。根结点，叶结点和内部结点在决策树中都表示一个具有某种属性或多个属性的数据集。

在ID3算法和C4.5算法对结点进行分裂时，依据的是信息熵和信息增益来决定进行是否分裂，当决策树的结点满足某种条件的时候，就会进行结点的分裂和结点的终止分裂。根结点是决策树最顶端的结点也是最大的结点，决策树通过内部结点的不断地分裂中产生新的内部结点和新的叶结点，叶结点代表的含义是该结点将不能继续分裂，是某种属性数据集的终止结点。而非叶结点的内部结点是具有多种属性的数据集，该结点根据信息熵和信息增益可以进一步分裂成为下一个叶结点或非叶结点。在决策树中需要分裂的最大数据集就是根结点，内结点是数据集分类的输入，叶结点是数据集分类的输出［3～6，10～12］。

2）决策树算法的特点

ID3算法和C4.5算法都是采用递归算法对树内的结点不断进行分裂。在决策树结点分裂的过程中，从根结点到新结点的每一条路径都相对应于一条相应的规则，在决策树中的每一条规则都可以转化为相应的IF-THEN规则。事实上IF-THEN规则能够使得决策树较快地对新数据进行分类，通过相应的IF-THEN规则以及结点属性就可以新数据进行分类，生成新的决策树，直到所有决策树的结点都成为叶结点为止。

3 信息熵和信息增益简介

3.1信息熵

1）ID3算法和C4.5算法都是基于信息论的决策树算法，在信息论中信息量，信息熵，条件熵，平衡互信息量和信息增益是其中重要的基本概念。

在信息论中，采用信息熵来衡量信息的不确定性。在信源中由于信息的发送者发送的信息是多种多样的，某些信息是已知的，而某些信息是未知的，对于已知的信息是可以确定的，而对于新信息是不能够确定的，因此在信息源中某些信息存在不确定性。

2）d是某个信息熵的值

分析和讨论：

（1）因此当d的值十分小的时候，这个时候训练集的纯度就越高。当信息熵值越接近于0时，这时训练集的纯度就越高，这时该数据集的确定性就越明显。

（2）当d的值十分大的时候，这时信息熵的值就越大，同时这个训练集的纯度就越差。当训练集的纯度越差，那么这时该数据集存在不确定性的程度就越明显。

根据以上的分析和讨论有以下的结论：

信息熵：在信源中能够反应整体信源的不确定性［10～12］。

某个信息源总是发送相同的信息，那么接收者就不存在不确定信息，此时信息源的信息熵就不为零。在信息源中造成不确定性的原因是发送者发送的信息不总是相同的信息，新信息是未知的信息，而这些新的未知信息就表示了信源的不确定性。由于在一棵决策树中每一个内部结点都是一个信源，因此信息熵能够反应每一个内部结点的不确定性。

3.2信息增益

1）信息增益与信息熵是两个概念：信心增益：在ID3算法和C4.5算法中是计算数据集是否进行分类的依据，也就是决策树的结点是否进行分裂的依据。而信息熵：信息不确定性的衡量指标。

2）d是某个信息增益

（1）当d的值十分小的时候，这时信息增益将十分地接近于0，当信息增益越小，这时该数据集被分裂的要求就越低。

（2）当d的值十分大的时候，这时信息增益越大远远大于0时，这时该数据集被分裂的要求就越明显。

在决策树形成过程中，最重要的部分是对决策树分裂结点的选择，最常用的计算方法是信息增益。由于信息增益越大的属性分裂数据集的可能性越大［10～12，3～6］。因此，如果一个决策树的某个结点的信息增益越大，那么该结点的数据集被分裂的可能性就越大，同样如果一个决策树的某个结点的信息增益越小，那么该结点的数据集被分裂的可能性就越小。在决策树算法的结点分裂之中，要求每一次都选择其信息增益最大的属性作为决策树的新结点。

4 MMTD算法技术简介

4.1中介真值程度度量知识简介

中介逻辑将事物的属性描述成三种状态，事物属性的两个对立面和对立面的中间过渡状态。在中介真值程度度量方法中，提出了事物超态属性概念，该方法符合中介思想事物的属性并且被划分为五种状态：事物的两个对立面，对立面的中间过渡状态和事物超态对立面［1-2］。这里用符号表示为～P，P与╕P，超态+p与超态╕+p。现用数轴将以上的描述的概念表达如下［1-2］：

图1 中介真值程度度量一维函数图

对数轴y=f(x)表示的含义有以下说明［1～2］：

数轴上用符号P与╕P分别表示事物对立面的两个属性，符号～P表示反对对立面的中间过渡状态达事物的属性。

1）如果数轴上数值点的位置逐步接近P，则事物A所具有P的属性逐步增强。

2）如果该数值点的位置落在真值╕P和P的取范围之间，则事物A的属性就部分地具有╕P的属性，同时又部分地具有P的属性。

3）如果数轴上数值点的位置逐步接近╕P，则事物A所具有╕P的属性逐步增强。

4.2中介真值程度度量中的距离比率函数

在中介真值程度度量的方法中，数轴上某数值点通过距离比率函数来计算事物所具有属性的强弱。

定理1给定y=f(x)∈f(X)，ξ(h(y))=h(y)，则有［1～2］

1）当αF+εF＜y＜αT-εT时，gT(x)∈(0,1)，gF(x)∈(0,1)；

2）当y＞αT+εT时，gT(x)＞1；当y＜αF-εF时，gF(x)＞1；

3）当y＜αF-εF时，gT(x)＜0；当y＞αT+εT时，gF(x)＜0；

4）gT(x)+gF(x)=1。

（1）相对于P的距离比率函数［1～2］

5 MMTD方法的应用

5.1决策树结点信息增益的计算

1）信息增益的衡量函数：

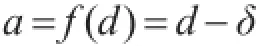
a表示某个值，d是某一个信息增益，δ是一个很小的值，δ≈0。

以下对信息增益值计算的分析和讨论：

2）当a=d-δ＞0时

在一棵决策树的生成过程中，如果决策树的非叶结点的信息增益越大，则对该结点分裂的作用越大，信息增益越大，则该结点就越有可能被分裂多个其它的结点。为了描述和计算信息增益由小变大的过程，在本文中将信息增益与一个十分小的值进行比较和衡量，当信息增益与最小值的差值逐渐变大的过程中，则此时信息增益在不断的变大过程中。

因此如果a＞0的值越大，d与δ的差值也就越大，并且这时d的值在变大的过程中。如果d在逐渐变大，当差值a大于0时或十分的大于0时，d就远大于δ。当d变大的时候，这时结点的信息增益就越大。当信息增益越大，远远大于0时，这时该数据集被要求分裂的程度就越明显。在本文中当结点的信息增益越强的时候，就用真值1表示。

如果结点数据集的信息增益越小，那么结点分裂的可能性就越小，因此当d与很小的值δ十分接近时，此时该信息增对结点分裂的意义将变得很小。信息增益越小，则该结点被分裂的可能性就越小。因此当d十分接近于δ，此时信息增益接近于0，该数据集被要求分裂的程度就越低。在本文中当结点的信息增益越弱的时候，就用真值0表示。

3）当a=d-δ＜0时

在一棵决策树生成的过程中，非叶结点的内部结点为了进行不断地分裂生成新的结点，则需要该结点的信息增益尽可能的大。如果信息增益值十分接近于极小值δ时，该结点被分裂的可能性将十分的小，这样的信息增益对结点的分裂是没有作用的，因此以在本文提出的算法中要求信息增益尽可能的大，这样对于决策树的生成是有作用的。

这时信息增益将十分地接近于0，当信息增益的值越小越接近于0时，这时该数据集被分裂的要求就越低，这时训练集的纯度就越高。在本文中当结点的信息增益越弱的时候，使用真值0表示。

5.2中介对网络流量的描述

以下用中介真值程度度量方法对决策树的分裂做以下的研究：

数轴y=f(x)上有P，～P，╕P三个数据区域，P代表信息增益强，╕P代表信息增益弱，～P代表信息增益半强半弱。

5.3距离比率函数

从数轴上y=f(x)可以知道，在数轴上以～P为对称中心，左右分别为╕P和P。

图2 中介真值程度度量一维函数的应用

y=f(x)的值落在三个值域范围(αr+εr,αl-εl)，(αr-εr,αr+εr)(αl-εl,αl+εl)。～P的区域为(αr+εr,αl-εl)，╕P的区域为(αr-εr,αr+εr)，P的区域为(αl-εl,αl+εl)。P的真值为1，╕P的真值为0

相对于P的距离比率函数

通过距离比率函数hT(x)对y值的计算，如果有

1）若函数hT(x)=1，y值落在区域(αl-εl,αl+εl)，则此时信息增益强，其真值为1。

2）若函数hT(x)=0，y值落在区域(αr-εr,αr+εr)，则此时信息增益弱，其真值为0。

3）若函数hT(x)=y值落在区域(αr+εr,αl-εl)，则此时信息增益半强半弱。

6 结语

决策树算法是一种机器学习算法，用于对数据的分类。决策树的生成过程中采用递归算法使得决策树的结点能够不断地分裂，从而生成一棵决策树。在ID3算法和C4.5算法中信息熵和信息增益是决策树的两个重要指标，因此在本文中采用MMTD算法对决策树的信息增益进行研究。在本文采用由作者提出的公式与MMTD算法相结合在一起生成一种对决策树信息增益大小的衡量算法，将MMTD算法在决策树中进行应用是本文的创新点之一，提出一种信息增益衡量的算法是本文的主要创新点。

［1］洪龙，肖奚安，朱梧槚.中介真值程度的度量及其应用（I）［J］.计算机学报，2006（12）：2186-2193.

HUNG Long，XIAO Xian，ZHU Wujia.Medium Truth Scale and Its Applications（I）［J］.Journal of Computers，2006（12）：2186-2193.

［2］朱梧槚，肖奚安.数学基础与模糊数学基础［J］.自然杂志，1980（7）：723-726.

ZHU Wujia，XIAO Xi'an.foundations of mathematics and fuzzy mathematical foundation［J］.Chinese Journal of Na⁃ture，1980（7）：723-726.

［3］冯少荣.决策树算法的研究与改进［J］.厦门大学学报（自然科学版），2007，46（4）：496-500.

FENG Shaorong.Research and Improvement of Decision Tree Algorithm［J］.Xiamen University（Natural Science Edition），2007，46（4）：496-500.

［4］湛宁，徐杰.决策树算法的改进［J］.电脑知识与技术，2008（2）：1068-1069.

CHAM Ning，XU Jie.Improved Decision Tree Algorithm［J］.Computer Knowledge and Technology，2008（2）：1068-1069.

［5］谭俊璐，武建华.基于决策树规则的分类算法研究［J］.计算机工程与设计，2010，31（5）：1071-1019.

TAN Junlu，WU Jianhua.Classification Based on Decision Tree Algorithm rule［J］.Computer Engineering and De⁃sign，2010，31（5）：1071-1019.

［6］季桂树，陈沛玲，宋航.决策树分类算法研究综述［J］.科技广角，2007（1）：9-12.

JI Guishu，CHEN Peiling，SONG Hang.Review of re⁃search on decision tree classification algorithm［J］.Sci⁃ence and technology wide angle，2007（1）：9-12.

［7］龙际珍，任海叶，易华容.一种改进决策树算法的探讨［J］.株洲师范高等专科学校学报，2006，11（2）：64-66.

LONG Jizhen，REN Haiye，YI Huarong.An improved deci⁃sion tree algorithm［J］.Journal of Zhuzhou Teachers Col⁃lege，2006，11（2）：64-66.

［8］满桂云，林家骏.ID3决策树算法的改进研究［J］.中国科技信息，2007（13）：268-269.

MAN Guiyun，LIN Jiajun.ID3 decision tree algorithm im⁃provement research［J］.China Science and technology in⁃formation，2007（13）：268-269.

［9］杨学兵，张俊.决策树算法及其核心技术［J］.计算机技术与发展，2007，17（1）：43-45.

ZHANG Jun，YANG Xuebing.Decision tree algorithm and its core technology［J］.computer technology and develop⁃ment，2007，17（1）：43-45.

［10］胡江洪.基于决策树的分类算法研究［D］.武汉：武汉理工大学，2006：5-6.

HU Jianghong.Research on classification algorithm based on decision tree［D］.Wuhan：Wuhan University of Technology，2006：5-10.

［11］戴南.基于决策树的分类算法研究［D］.南京：南京师范大学，2003：8-15.

DAI Nan.Research on classification algorithm based on decision tree［D］.Nanjing：Nanjing Normal University，2003：8-15.

A Decision Tree Algorithm Based on MMTD

ZHU Lizhi
（Information Center，Nanjing University of Aeronautics and Astronautics，Nanjing210016）

decision tree is a kind of commonly used classification algorithm，since the ID3 algorithm has been related to the personnel to improve the algorithm，which appeares a variety of decision tree algorithm.When the decision tree is generated，the re⁃cursive algorithm is used to split the nodes of the decision tree.If the information gain of nodes is bigger，the probability of node splitting is greater.The ID3 algorithm and C4.5 algorithm in the information gain becomes an important basis for the node is split，so according to characteristics of the decision tree node split when the information gain function，this paper presents another algorithm to measure the size of the information gain，the algorithm with measure formula and the core algorithm——MMTD algorithm.The in⁃novation of this paper lies in MMTD algorithm in decision tree were used for the first time，and in the MMTD as the basis and the core of the algorithm is to achieve the measure of the size of the information gain.

MMTD，decision tree，information entropy，information gain，ID3 algorithm

TP393

10.3969/j.issn.1672-9722.2017.05.011

2016年11月10日，

2016年12月23日

朱俚治，男，工程师，研究方向：网络安全，计算机算法和技术。