直角双曲线内接三角形的垂心问题

王 庆

(苏州市职业大学 数理部，江苏 苏州 215104)

直角双曲线内接三角形的垂心问题

王 庆

(苏州市职业大学 数理部，江苏 苏州 215104)

目前，有关直角双曲线内接三角形垂心问题的研究还不多。本文用解析几何与射影几何的方法讨论这一问题，得出直角双曲线的内接三角形的垂心在原双曲线上的结论。

直角双曲线；射影几何；垂心

性质1：直角双曲线的内接三角形的垂心在原双曲线上。

证明(1)，首先用解析几何的方法讨论。

(1)

设：b=cosαcosβcosγ+cosαsinβsinγ+sinαcosβsinγ+sinαsinβcosγ，c=sinαsinβsinγ+sinαcosβcosγ+cosαsinβcosγ+cosαcosβsinγ，

(2)

取ω=arctan(-b/c)，则bcosω+csinω=0，该式可变形为

(3)

取S为直角双曲线上对应t=2ω的点，则RS的斜率为cos(ω-γ)/sin(ω+γ)。而由上式(1)可得RS⊥PQ，同理上式(2)可得QS⊥RP、上式(3)可得PS⊥QR。因此，S就是ΔPQR的垂心H，故H也在直角双曲线上。

下面用射影几何的方法证明，讨论中所用射影几何的概念及性质可见[1]。本文的讨论要多次用到射影几何的Steiner定理：设A，B是二次曲线上两定点，它们与二次曲线上动点P的连线的对应APBP是线束A，B间的射影映射，两线束间非透视的射影映射的对应直线的交点轨迹是二次曲线。为了给出性质1的证明，本文先给出如下的性质。

性质2：设A，B是双曲线上两定点，P是动点，则ΔABP的垂心是一条二次曲线。

确保无限制接入电网，余电上网全额收购。接入系统投资由电网公司负责。根据中共中央国务院《关于进一步深化电力体制改革的若干意见》电网企业应提高服务效率，保证无障碍接入。天然气分布式能源按“以热定电”的原则组织生产，具有综合能效高的特点，电网企业应支持和保证天然气分布式能源电力直供，余电优先上网和全额收购。根据国家能源局综合司关于电网企业回购电源项目自建配套送出工程有关事项的通知精神，电网公司应承担系统接入费用。由分布式能源公司先行垫支建设的，要在规定的时间内回购。

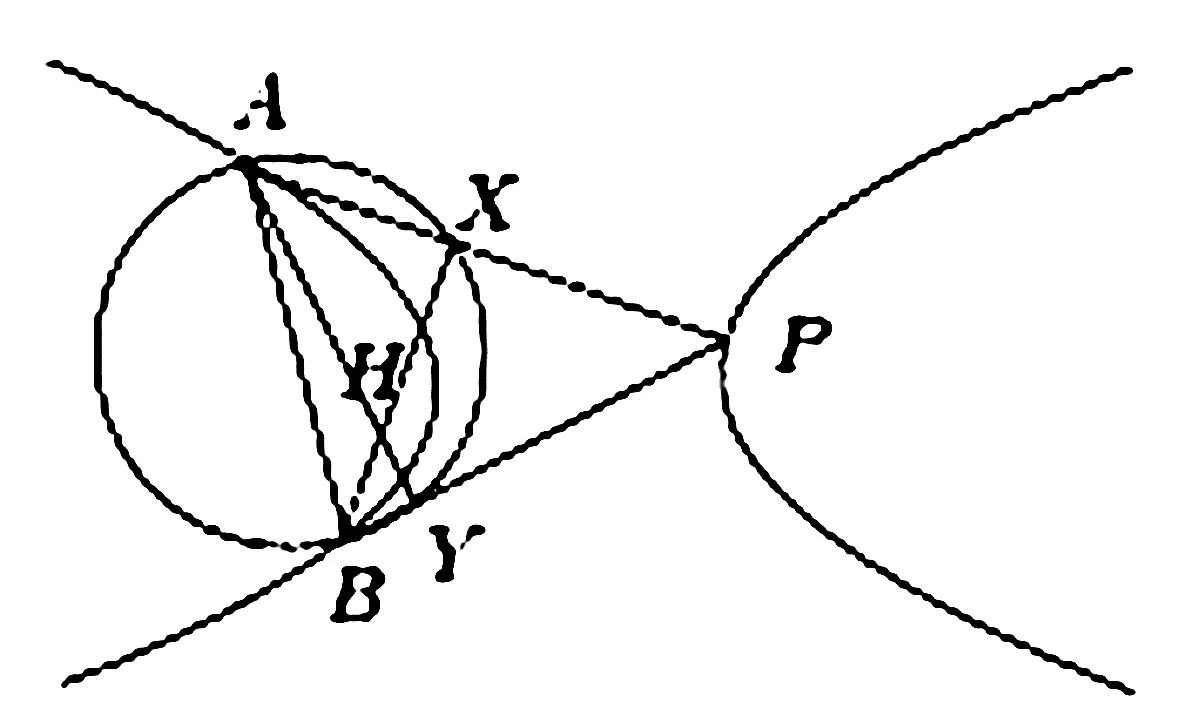
图1

证明：如图1，以AB为直径作圆，设PA，PB分别交圆于X、Y，AY与BX的交点H是ΔABP的垂心。对双曲线与圆用Steiner定理可得：

把性质中双曲线换成椭圆或抛物线也成立[2]。进一步可以证明，性质2中椭圆的内接三角形的垂心轨迹也是一个椭圆。

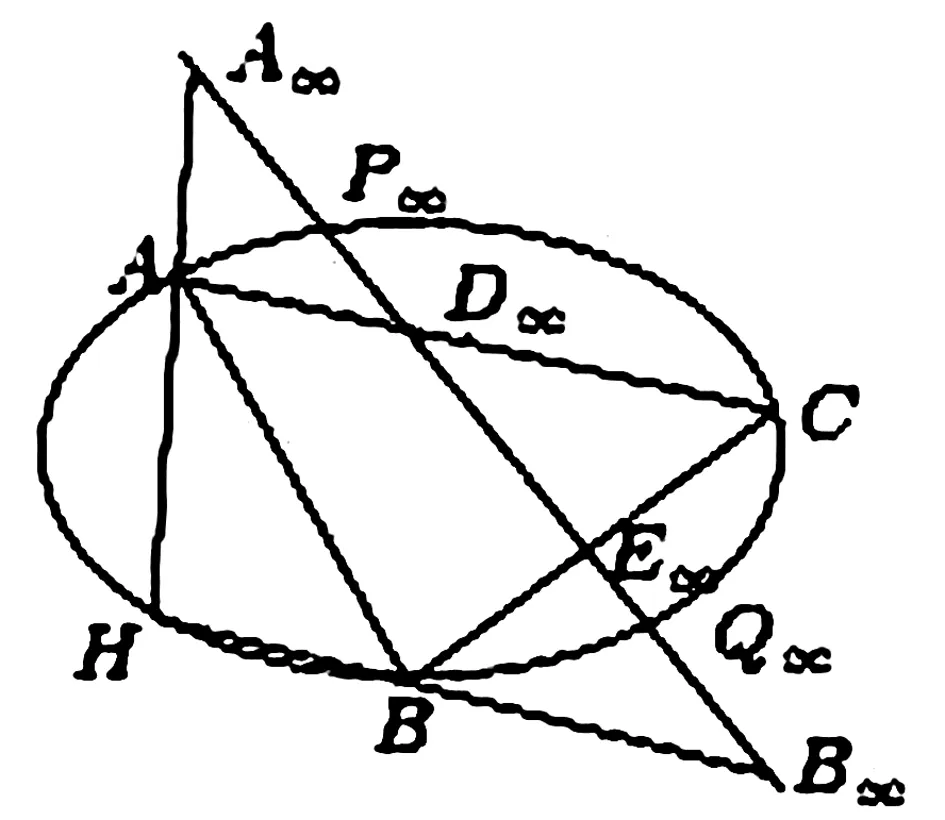
图2

证明(2)：设P、Q是直角双曲线Γ上的无穷远点，它们也是直角双曲线的渐近线与曲线的交点(切点)。过P、Q的直线互相垂直。设A、B、C是Γ上三点，H是ΔABC的垂心。图2画出了无穷远直线。不难知道，P→Q，A→E，B→D给出无穷远直线一个对合，过这一对合的对应点的直线互相垂直，对Γ上定点A、B，动点C用Steiner定理可得无穷远直线上双曲型射影映射

φ:P→P,Q→Q,D→E

记交比R(PQ,DE)=k，由[1]性质2.2.2，φ的不动点P、Q与它的任一对对应点的交比是常数，于是

R(PQ,AB)=R(QP,ED)=R(PQ,DE)=k，

这证明φ(A)=B。在定点A、B，动点C给出的射影映射下，AA的像是BB，由Steiner定理，H是直角双曲线Γ上点。

为了进一步的讨论先给出下面的性质，叫做Desargues对合定理。

性质3 一直线与完全四点形的三对对边交点是一个对合的三对对应点，过此完全四点形的二次曲线与直线的交点也是对合的对应点。

图3

证明：如图3所示，设Γ是过完全四点形ABCD的顶点的二次曲线，一直线与完全四点形的边交于E、E′，F、F′，G、G′，与Γ交于P、Q，对A、B用Steiner定理可得，

R(PQ,EF′)=R(PQ,FE′)=R(QP,E′F)。

这证明有对合φ1，使P→Q，E→E′，F→F′。同理，对B、C用Steiner定理可得对合φ2，使P→Q，F→F′，G→G′。对合由两对对应点决定，这两个对合都把P、F分别变为Q、F′。因此φ1=φ2，记为φ。对合φ也由E→E′、F→F′决定，与二次曲线Γ的选取无关，这证明了Desargues对合定理。

性质4 过(非直角)三角形的顶点与垂心的二次曲线是直角双曲线。

证明： 设Γ是过ΔABC的顶点与垂心H的二次曲线，D、E、F是三边上的垂足，DEF是由A、B、C、H给出的完全四点形的对角三点形，也是Γ的自极三点形。显然，自极三点形DEF的每一条边的两边都有二次曲线上点，而二次曲线的自极三点形的三边中总有一边与二次曲线没有交点，这证明Γ是双曲线。设A、B、D、E分别是AH、BH、AC、BC上的无穷远点，P、Q是Γ上无穷远点，如图2所示。由Desargues对合定理，P→Q,A→E,B→D给出一个对合。过A、E；B、D的直线分别垂直，由[1]§4.4习题8，过P、Q的直线也垂直。这证明Γ的渐近线垂直，Γ是等轴双曲线[3]。

[1] 周建伟. 高等几何[M]. 北京：高等教育出版社, 2003.

[2] 周建伟. 二次曲线局部与整体的关系[J].大学数学,2013,29(5):113-117.

[3] 王庆. 二次曲线垂直切线的研究[J].大学数学,2015,31(1):124-126.

[4] 石双双，杜旭东，白根柱.扩展的三角函数展开法及其应用[J].内蒙古民族大学学报(自然科学版)，2013(2)：142-144.

责任编辑：程艳艳

ProblemAboutOrthocenterofRectangularHyperbolicInscribedTriangle

WANGQing

(DepartmentofMathematicsandPhysics,SuzhouVocationalUniversity,Suzhou215104,China)

At present, the research on the problem about orthocenter of rectangular hyperbolic inscribed triangle is not much. This paper uses the methods of analytic geometry and projective geometry to discuss the problem, giving a conclusion that the orthocenter of rectangular hyperbolic inscribed triangle is on the original hyperbolic.

rectangular hyperbolic; projective geometry; orthocenter

2017-02-16

国家自然科学基金项目(11271277)；苏州市职业大学校级课题(SVU2015CGCX13)

王庆(1979-),男，江苏高邮人，副教授，硕士，主要从事从事高等几何方面研究。

O123.1

C

1009-3907(2017)04-0023-02