R软件在正态总体假设检验教学中的应用探讨
2017-06-01郭朝会
◎郭朝会
(重庆师范大学数学科学学院,重庆 401331)
R软件在正态总体假设检验教学中的应用探讨
◎郭朝会
(重庆师范大学数学科学学院,重庆 401331)
本文介绍了R软件在正态总体假设检验教学中的一些应用.通过教学实例阐述如何利用R软件进行直观教学,提高学生对假设检验原理的理解,从而培养学生的学习兴趣以及提高学生探索问题、解决问题的能力.
数理统计;假设检验;R软件
一、前 言
数理统计[1,2]是理工科高等院校的基础必修课程,在高等教育课程中占有举足轻重的地位.假设检验作为统计推断的三大内容之一,贯穿于数理统计学的始终.因此,它在数理统计这门课程中占有非常重要的位置.如何提高假设检验的教学,让学生深刻理解假设检验的统计原理是数理统计教学的重点和难点.而传统的教学方法,很难形象直观地展现假设检验的统计原理,使得学生对假设检验原理的理解有一定的难度.随着现代科技的飞速发展,许多现代教学手段可以运用到学生学习以及教师教学中来.最流行的方法之一就是使用教学软件来辅助教学,展现统计的思想和方法,提高统计教学的效率.目前应用最广泛的教学软件工具无疑是MATLAB、SPSS、SAS等商业软件.由于在大学教育中我国越来越重视知识产权,因此,教学单位若想将上述商业软件应用于日常教学,必须有足够的经费支持.然而,这对于自主学习的学生或教师来说带来了一定的困难.R软件是由奥克兰大学统计学系的Ross Ihaka和Robert Gentleman共同创立,它功能强大、操作简单,更重要的是它是一款完全免费的统计分析软件.R软件提供了有弹性的、互动的环境来分析和展示数据,它一般用于统计建模、统计计算、数据处理等.R软件还有一项很重要的功能,就是它包含了许多有用的程序包,到目前为止,R软件官方网站就已经提供了超过七千个程序包,涵盖数理统计学、金融统计学、生物统计、经济管理、社会学等.其次,通过加载这些程序包可以读取源代码,并可以根据自己的需求改写其源代码得到适合新问题的程序.因此,相比于商业软件,R软件在数据分析和统计建模等方面毫不逊色.因此,正是由于R软件的独特之处使得它特别适合辅助数理统计教学[3,4].
在实际问题中大多数数据都服从或近似服从正态分布,所以,本文重点考虑如何利用R软件实现单个正态总体均值的假设检验直观教学以及提高学生动手操作的能力.
二、R软件在单个正态总体均值假设检验中的应用
首先,我们回顾一下单个正态总体均值假设检验的统计理论.根据假设检验思想:若原假设成立导致了不合理的现象发生,则我们就应该拒绝原假设否则接受原假设,即通过限制犯第一类错误的概率来求得拒绝域.设X1,…,Xn是来自N(μ,σ2)的一组独立同分布样本,现我们考虑如下的双边检验问题H0:μ=μ0,H1:μ≠μ0.
① 若方差σ2已知,因此,根据假设检验的思想,我们有

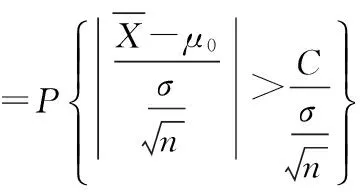
(1)
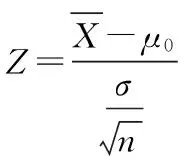
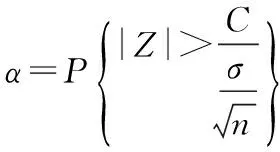
(2)
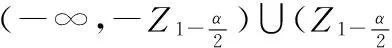
② 若方差σ2未知,统计量Z中包含未知参数σ,因此,需要构造新的统计量.根据抽样分布定理,我们可知
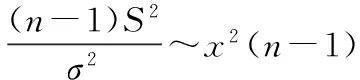
再由t分布的定义知
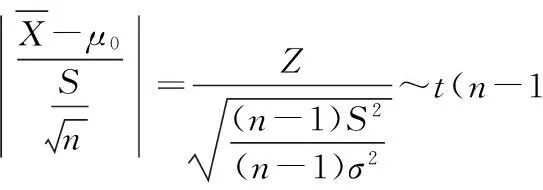
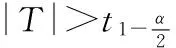
下面我们通过一个例子来阐述单个正态总体均值的假设检验问题.
例1[5]正常男子血小板计数均值为225×109/L,今测得20名男性油漆作业工人的血小板计数值(单位:109/L)如下:220,188,162,230,145,160,238,188,247,113,126,245,164,231,256,183,190,158,224,175,问油漆工人的血小板计数与正常成年男子有无差异?
解 根据题意需检验
H0:μ=μ0=225,H1:μ≠μ0.
我们首先需要判定此组数据是否来自于正态分布,因此,我们采用Shapiro-Wilk(夏皮罗-威尔克)W统计量做正态性检验,相应理论可参考文献[5].在R软件中可用shapiro.test命令来做检测,检测结果如下:
shapiro.test(x)#x代表此组数据所构成的向量
Shapiro-Wilk normality test
data:x
W=0.95063,p-value=0.3768
根据结果可知p-value=0.3 768>α=0.05,则可判定此组样本来自于正态总体.又因为此组数据的方差未知,因此,采用t检验.针对这个检验问题本文编写了一个程序来实现,相应的代码和结果如下:
##编写的单个正态总体均值假设检验的代码
normal.mean.test=function(x,mu0,sigma,alpha){
#x样本观测值;mu0均值;sigma标准差;alpha显著性水平
n=length(x)#待测样本个数
x.mean=mean(x)#计算样本的均值
if(sigma=="known"){#判定总体方差是否已知,若已知则做如下命令
Z=(x.mean-mu0)/(sigma/sqrt(n))#计算Z统计量
result=abs(Z)>qnorm(1-alpha)#计算拒绝域
if(pnorm(Z)<0.5){p.value=2*pnorm(Z)}else{
p.value=2*(1-pnorm(Z))}#计算p值
if(result=="TRUE")print("拒绝原假设")
list(Z=Z,p.value=p.value)#输出结果
}else{#总体方差未知,做如下命令
x.var=sd(x)#计算样本标准差
T=(x.mean-mu0)/(x.var/sqrt(n))#计算T统计量的值
if(pt(T,n-1)<0.5){p.value=2*pt(T,n-1)}else{
p.value=2*(1-pt(T,n-1))}#计算p值
result=abs(T)>qt(1-alpha,n-1)##计算拒绝域
if(result=="TRUE")print("拒绝原假设")
list(T=T,p.value=p.value)#输出结果 }}
normal.mean.test(x,mu0=225,sigma="unknown",alpha=0.05)##调用所编写的函数结果如下:
[1]"拒绝原假设"
$T
[1]-3.478262
$p.value
[1]0.002516436
一方面,从第一条结果可知我们应该拒绝原假设,即油漆工人的血小板计数与正常成年男子有显著差异.另一方面,在显著性水平是α=0.05的情况下,p-value=0.002 516 436<α=0.05,此结果也说明应该拒绝原假设.另外,在R软件中可以利用命令t.test来检验方差未知的正态总体的均值检验,针对此例题调用t.test函数结果如下:
t.test(x,alternative="two.sided",mu=225)
One Sample t-test
data:x
t=-3.4783,df=19,p-value=0.002516
alternative hypothesis:true mean is not equal to 225
95 percent confidence interval:
172.3827 211.9173
sample estimates:
mean of x 192.15
此结果跟我们编写normal.mean.test函数所得结果一致,即油漆工人的血小板计数与正常成年男子有显著差异.
三、总 结
目前数理统计教学的理论抽象、公式复杂,因此,很多学生在学习这门课程时存在很多问题,尤其对于假设检验这一节的内容.如能将R软件引入假设检验的教学中,不仅可以加深学生对假设检验知识的理解,还可以使学生摆脱烦琐的计算,从而很大程度上提高了学生处理数据的能力.本文结合实例,介绍了R软件在单个正态总体的均值假设检验中的具体应用.首先,R软件能够直观地画出统计量的密度函数曲线图,从而高效地解决假设检验中很多教与学的问题.其次,R软件给我们提供了很多经典的统计命令(如本文介绍的shapiro.test、t.test等),通过直接调用就能获得相应的统计分析结果.最后,当代教师不仅要会讲授教材上的理论知识,还需利用统计软件将理论知识与实践相结合,从而促进教师自身的学术造诣和实践教学能力的提升.
[1]孙荣恒.应用数理统计(第二版)[M].北京:科学出版社,2003.
[2]刘琼荪,钟波,荣腾中,李曼曼.概率论与数理统计[M].北京:高等教育出版社,2014.
[3]赵军,杨琳.R软件在大学数学教学中的应用探讨[J].高教学刊,2016(7):93-95.
[4]程胜.R统计软件及其在《时间序列分析》实践教学中的应用[J].教育教学论坛,2014(41):173-175.
[5]薛毅,陈立萍.统计建模与R软件[M].北京:清华大学出版社,2007.
重庆师范大学基金项目资助(16XLB019).
