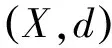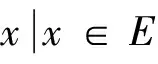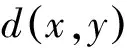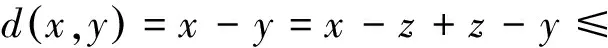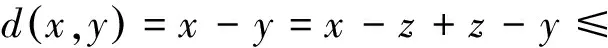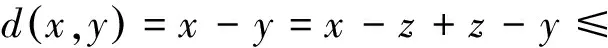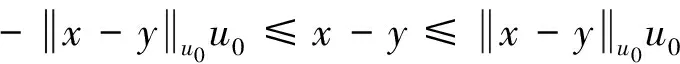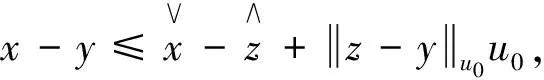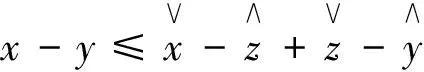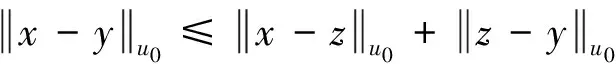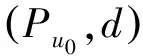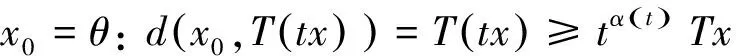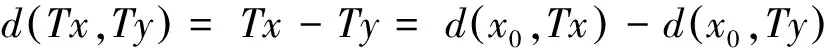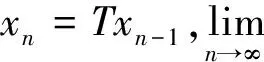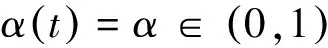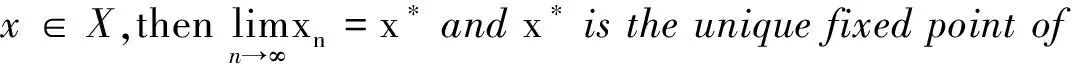u0-锥度量空间上新的映射不动点定理
2017-06-01袁国常雷国营
袁 轩, 袁国常, 雷国营, 张 宙
(1.三峡大学 水利与环境学院, 湖北 宜昌 443000;2.湖北三峡旅游职业技术学院, 湖北 宜昌 443100)
u0-锥度量空间上新的映射不动点定理
袁 轩1, 袁国常2*, 雷国营2, 张 宙2
(1.三峡大学 水利与环境学院, 湖北 宜昌 443000;2.湖北三峡旅游职业技术学院, 湖北 宜昌 443100)
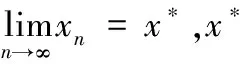
锥度量;u0-锥度量空间; 单增映射; 不动点
在文献[1]中,Potter在Hilbert空间上介绍了α-凹算子,给出了关于这类算子非线性特征问题Ax=λx解的存在性.随后,这类算子的条件和结论被人们减弱和改进[3].文献[3]进一步推广了α-凹算子,得到新的不动点定理.由此自然地产生一个问题,能否在一般集合上推广α-凹算子,进而讨论其不动点问题呢?解决这一问题是困难的.文献[4-5]给出锥度量的概念,这使得在一般集合上讨论相关映射的不动点问题成为可能.本文以文献[4-5]给出的锥度量概念为基础,建立了u0-锥度量空间理论,并引入满足条件H的映射T,讨论了T的不动点问题.最后给出的例子说明映射T正是Banach空间上的α-凹算子在一般正齐性集X上的推广.
1u0-锥度量空间
设E为实Banach空间,θ为其零元,P为E中非空锥体,E由P导入的半序记为“≤”,即u,v∈E,u≤v,且u≠v时,记为u 本文总假定X为非空正齐性集,(X,d)为完备的锥度量空间. 引理1[7]设Pu0中的两元u,v可比较,并且u≤v,则u-v∈Pu0. 现对X→X的映射T作以下假设H:T为单增映射,对∀x∈X,存在x0∈X,使得T满足: 引理3设T:X→X满足条件H,则∀x∈X, 证明设tx=y,则x=t-1y,代入条件H中的不等式,有 证明由引理3,对∀y∈X,有 证毕. (1) 这与推论2矛盾.故t0<1,且 (2) (3) (4) (5) 由推论2得到 综上述得到 (6) 再由T的单增性得到 v0≤v1≤…≤v0≤…≤wn≤…≤w1≤w0. (7) 如此得到 由 及推论2得 取正整数n,p,由T的假设条件,(7)和T的单增性以及 得: 设有x#∈X,使得Tx#=x#. 记s1=sup{(s>0|d(x0,x*)≥d(x0,sx#)}.显然d(x0,x*)≥d(x0,s1x#).如果0 得x*=x#.证毕. 1) 当x与y可比较,分3种情况:设x≥y,z∈Pu0, (1)若z与x,y均可比较,此时 ; (2)若z与x,y之一不可比较,不妨设z与y不可比较,此时 ; (3)若z与x,y均不可比较, 此时 . 注2定理1在证明不动点的存在性时没有用到范数和锥的正规性,所以定理2更具有一般意义. [1]POTTERAJB.ApplicationsofHilbertsrojectivemetrictocertainclassofnon-Homogeneousoperators[J].QuartJMathOxfond, 1997, 28(2):93-99. [2] 郭大均. 非线性泛函分析[M].2版.济南:山东科学技术出版社,2001. [3] 翟成波, 王文霞, 张玲玲. 一类凹与凸算子的推广[J].数学学报, 2008, 51(3):529-540. [4]HUANGLG,ZHANGX.ConemetricspacesandfixedpointtheoremsofContractivemappings[J].JMathAnalAppl, 2007, 332:1467-1475. [5] 张 宪. 锥度量空间中Lipschitz型映射的公共不动点定理[J].数学学报, 2010, 53(6):1139-1148. [6] 张 宪. 序压缩映射的不动点定理[J].数学学报, 2005, 48(5):973-978. [7] 袁国常. 锥压缩逼近算子的不动点定理[J].西南师范大学学报(自然科学版), 2011, 36(5):44-47. A new fixed point theorem of mappings onu0-cone metric space YUAN Xuan1, YUAN Guochang2, LEI Guoying2, ZHANG Zhou2 (1.College of Hydraulic and Environmental, China Three Gorges University, Yichang, Hubei 443000;2.Department of Basic Course, Three Gorges Travel Vocational College, Yichang, Hubei 443100) conemetric; u0-conemetric;singleincreasemapping;fixedpoint 2016-05-23. 1000-1190(2017)01-0007-05 0177.91 A *通讯联系人. E-mail: ygc510@163.com.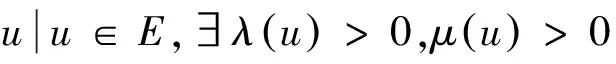
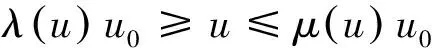
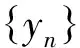
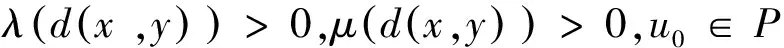
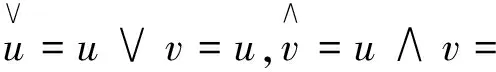
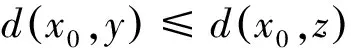
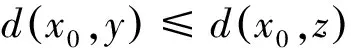
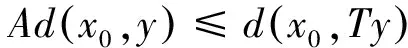
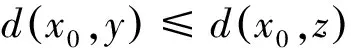
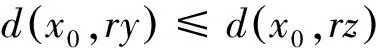
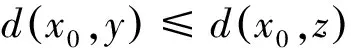
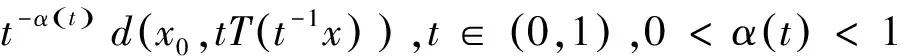
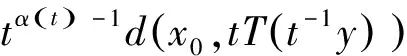
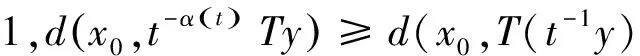
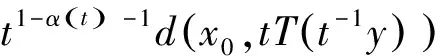
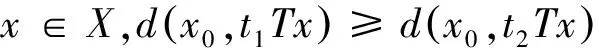
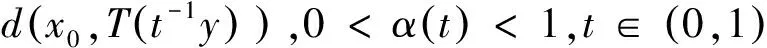
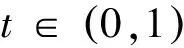
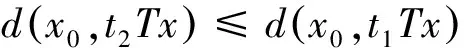
2(X,d)上满足条件H的映射的不动点定理
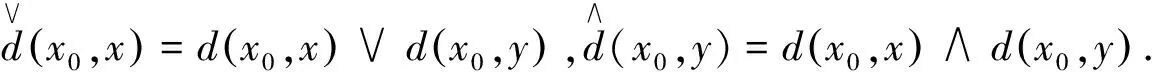
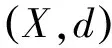
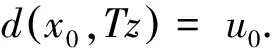
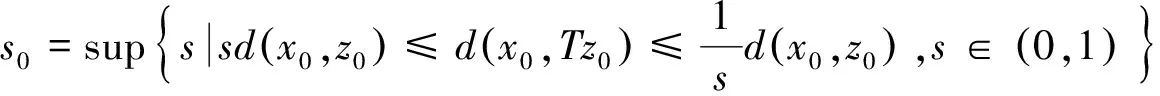
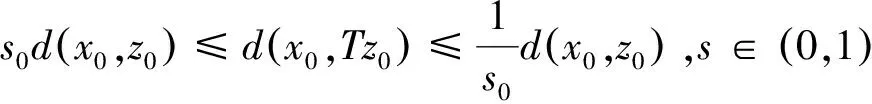
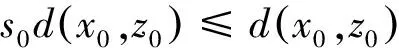
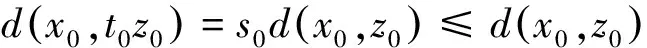
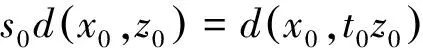


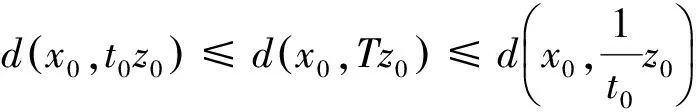
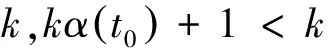
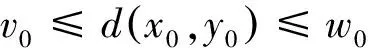
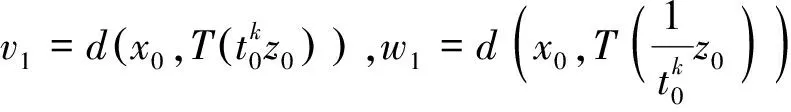
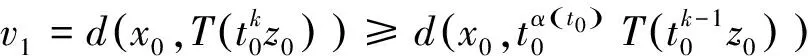
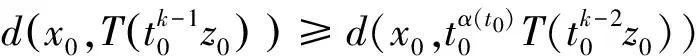
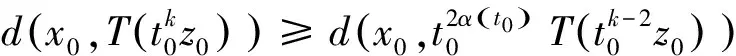
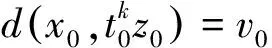
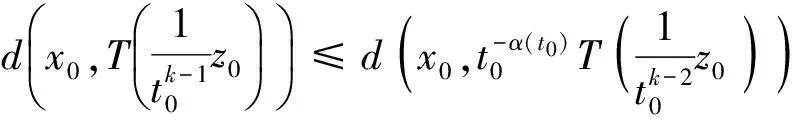
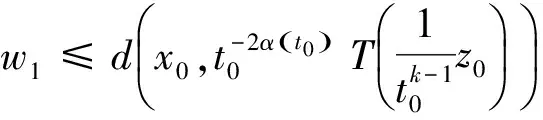
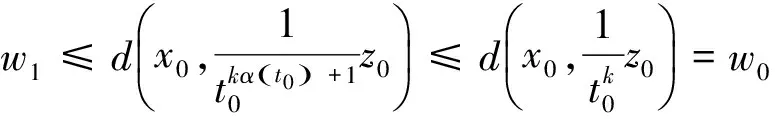
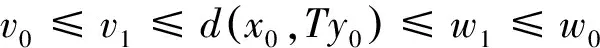
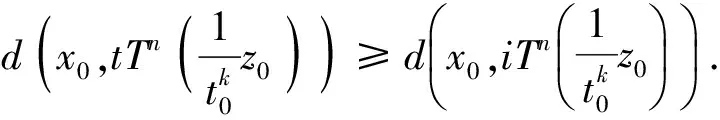
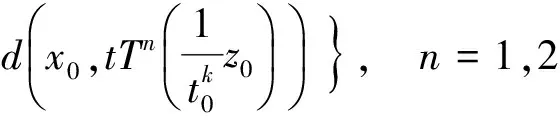
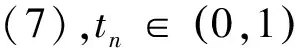

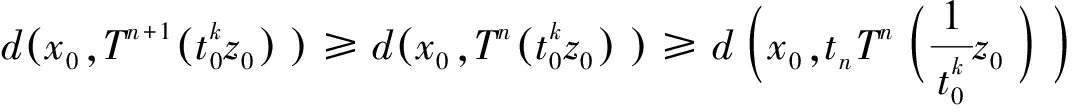
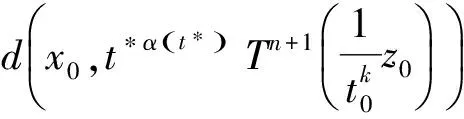
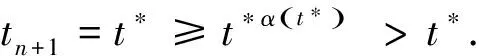
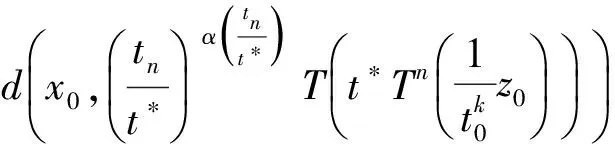

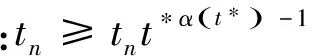
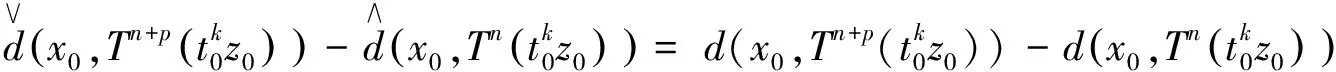
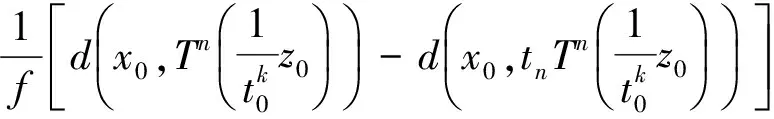
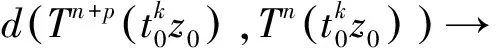
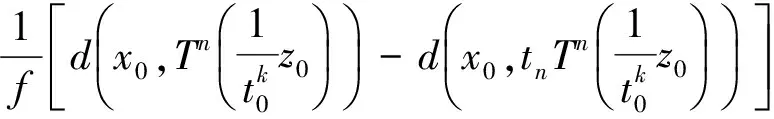
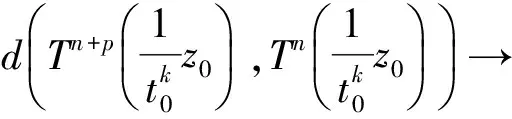
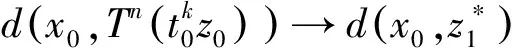
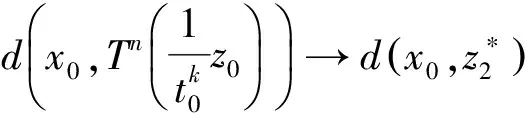
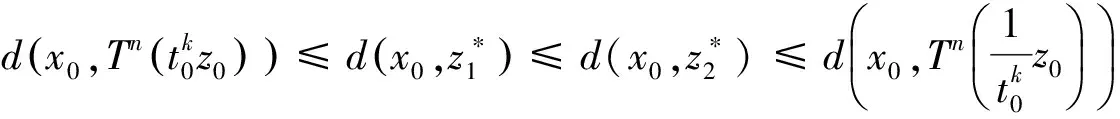
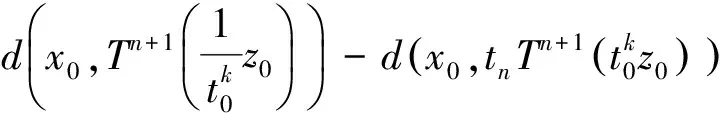
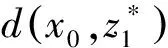
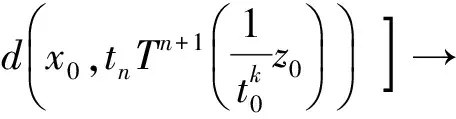
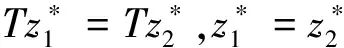
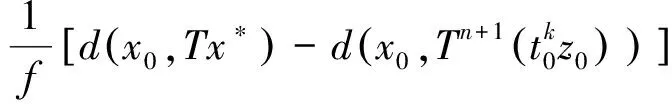
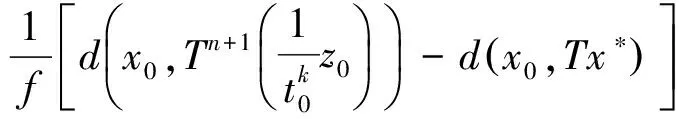
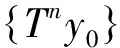
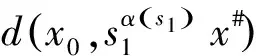
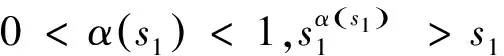
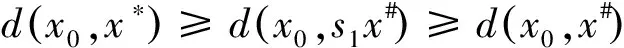
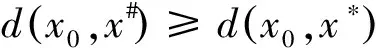

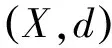
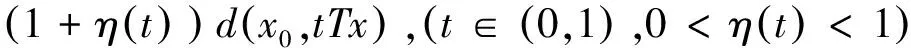
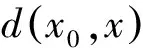
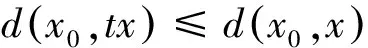
3例子