应用反例，培养数学思维能力

2017-06-01江苏省苏州工业园区金鸡湖学校

数学大世界 2017年12期

江苏省苏州工业园区金鸡湖学校沈奕

应用反例，培养数学思维能力

江苏省苏州工业园区金鸡湖学校沈奕

在初中数学的教学过程中，常常会发现学生们因为对知识理解有偏差，或者因为其他原因而出现多种多样的问题。因此，老师可以将学生们的这种“错误”巧妙地融合到反例中，加强学生们对问题的认识度，进而培养他们的数学思维能力。文章从多个角度，缜密思维；辩证真假，灵活思维；透析概念，抽象思维；学以致用，创新思维四个方面，阐述了如何在初中数学教学中应用反例，培养学生的数学思维能力。

初中数学；数学教学；反例；思维能力

新课程标准指出：在教学过程中应注重多方面培养学生们的思维能力。初中数学是锻炼学生们正确理解数学思维并灵活加以应用的重要阶段。在数学教学过程中，常常会发现学生们因为对知识理解有偏差，或者因为其他原因而出现多种多样的问题。因此，我在教学过程中，将学生们的这种“错误”巧妙地融合到反例中，加强学生们对问题的认识，进而培养学生们的数学思维能力。

一、多个角度，缜密思维

在众多人的认识当中，都认为研究数学的人们思维都十分缜密，的确如此，数学知识的理解和掌握确实需要我们有严谨的态度和缜密的思维，但是在日常的练习或考试中，学生们就会发现有些错误的出现往往并不是因为自己不会做，而是因为自己在解题的过程中太马虎大意，这就对我们在思考问题时的逻辑思维提出了更高的要求。反例应用，使学生们可以从多个角度看问题，很好地提升了学生们思维的严密性。

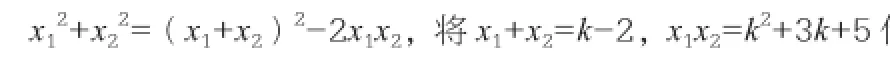
反例的应用需要学生们掌握好知识的脉络，有足够好的知识梳理能力。它不仅给予了学生们从另外的角度理解知识的一种方法，还对学生们的思维能力提出了更高的要求，巧妙应用反例，有利于缜密数学思维。

二、辩证真假，灵活思维

在数学的证明题中，我们习惯的思维是从题目的正面入手，根据题目的已知条件从正面解决问题，但是有时候我们会发现从正面解决问题会很难，在这个时候不妨试试应用反例进行证明。在数学问题中，有许多时候应用反例解决问题反倒使我们的思维更加灵活。

如在数学中经常出现真假命题的判断，利用反例，就可以很好地解决此类问题。例如：已知两个实数a、b不等于0，如果a＜b，那么1/a＞1/b。学生们代入了几组数据，结果验证这个命题是正确的。我就为学生们列举了其中的一个反例：假如a=-2，b=1，代入其中时就会发现1/a＞1/b这个命题是假的，一个反例就可以把这个问题解决了。学生们纷纷询问反例应当如何给出，我就带领学生进行进一步的分析：由于1/a-1/b=（b-a）/ab，从题中我们已知a＜b，所以可以知道只有在ab＞0时，1/a-1/b才大于0，命题才成立，所以反例就应该在ab＜0的范围内去寻找，我们又已知a＜b，所以在这个范围中找反例就好了。这样灵活地进行分析总结，很大程度地降低了做题的盲目性，提高了做题的效率。

运用反例其实是一种很好的逆向思维能力，当按照常规的思维进行求解比较复杂时，需要学生们学会换位思考，应用逆向思维进行求解，往往会“柳暗花明又一村”。

三、透析概念，抽象思维

大多数数学概念都比较抽象，如一元二次方程、无理数、椎体等，如果单单拿出来为学生们讲解其概念，学生们听起来就会感觉迷茫，再加上有的概念不仅抽象，还十分相似，这就会使学生们对知识的应用产生混淆，更加打击学生们学习的积极性。因此，在教学中应用反例，帮助学生们对一些易混概念进行比较学习，使学生们更好地抓住知识的本质，提高学习兴趣。

有时候学生们对概念的理解常常步入误区，例如：无限不循环的小数为无理数，学生们就会经常将其误解为：无限小数或者是带有根号的数都是无理数。为了使学生们对概念加以区分，我为学生们举了以下反例，如：2.13131313……，这样的无限循环小数便不是无理数。还有当根号内为一个数的平方时，也不是无理数。学生们在以后解题时，就能将其与反例进行对比，减少了失误。又如：分式方程的概念为：分母里含有未知数的方程叫作分式方程。有时候学生们对一些分母里含有参数的方程也会误以为是分式方程，我就为学生们列举了一个关于x的方程：（3x+6）/b=3，虽然分母里含有b，但是其不是未知数，因此不是分式方程。还有命题：如果一个多边形的每条边都相等，那么它是正多边形。如果一个多边形的每一个角都相等，那么他也是正多边形。当我们在做题时想到菱形和矩形这两个反例，就能很容易判断出该命题为假命题了。

应用反例有助于学生们对易混知识进行对比学习，区别其中的差异，更加理解知识之间的本质和联系，在教学的过程中达到使学生们不仅“知其然”，还要“知其所以然”的教学目标，使学生们简简单单地区分概念，轻轻松松地掌握知识。