γ-TiAl合金铣削加工表面残余应力研究

（西北工业大学机电学院，西安710072）

γ-TiAl合金作为一种新型高温结构材料，因其极低的密度及其他一系列独特的物理和力学性能（高比刚度、高比强度、良好的抗氧化性等），在航空航天、汽车工业等领域的零部件轻量化设计中受到高度重视，成为合金化合物中的研究热点[1]。目前，γ-TiAl合金已用于制造压气机叶片，涡轮高压和低压叶片，发动机喷嘴，以及汽车排气阀等重要零部件，展现出巨大的潜力与应用前景。然而，TiAl合金具有较低的塑性延展性、较低的断裂韧性及较小的热传导系数，在机械加工过程中常出现切削力大、切削温度高、刀具磨损严重、烧伤以及微裂纹等问题，目前已被确定为难加工材料[2-5]。

Mantle等[6-7]使用钻孔法测量了γ-TiAl铣削加工后工件表面残余应力，发现残余应力性质均为压应力，且高达500MPa，通过监测切削过程中的刀具状态，分析判断出刀具磨损和切削速度是影响残余应力的主要因素。后来，Hood等[8]在槽铣γ-TiAl合金时发现类似现象，即工件表面同样为残余压应力，且应力层深度达450μ m 。本文通过设计4因素4水平的正交试验，以γ-TiAl合金为研究对象，探究切削参数对残余应力的影响规律，并进行灵敏度分析[9]，为寻求切削参数的优选区间奠定理论基础。

1 γ-TiAl合金铣削试验

试验材料为γ-TiAl合金，工件几何尺寸为176mm×70mm×18mm，切削试验方案如图1所示。其中X轴表示步进方向，Y轴表示进给方向。试验机床选用VMC850数控铣床，主轴最大转速为8000r/min，最大功率为22kW，干切削。刀具选用Φ10mm整体硬质合金4刃平底立铣刀，牌号为K40。铣削力采用Kistler 9255B三向动态压电式测力仪进行测量，力测量信号图表明Fx、Fy、Fz均随切削时间的变化呈现周期性变化，选取每向力信号图连续10个最大峰值信号，然后计算平均值作为各向铣削力大小值，最后进行三向铣削力值合成总切削力；切削温度采用FLUKE Ti400Thermal Imagers红外测温仪，残余应力采用X射线应力分析仪Proto-LXRD MG2000进行测量，针对各个加工区域的加工表面，沿中心线进给方向等间隔取3个点，分别测量X向（步进方向）和Y向（进给方向）残余应力，为了使试验数据更准确可靠，分别求取各方向3个测量值的平均值。

本试验选用正交试验设计方案[10]，设计4因素（铣削速度、铣削深度、每齿进给量、铣削宽度）4水平L16（44）正交表。根据试验测量结果，由于Y向的残余压应力值比X向小，故本文仅对X向残余应力进行研究。铣削参数及测量结果如表1所示。在试验过程中，将整块工件表面等分成16个区域，每个区域完成一组对应的切削参数，且每加工一个区域需换一把新刀，以保证切削初始条件的一致性。

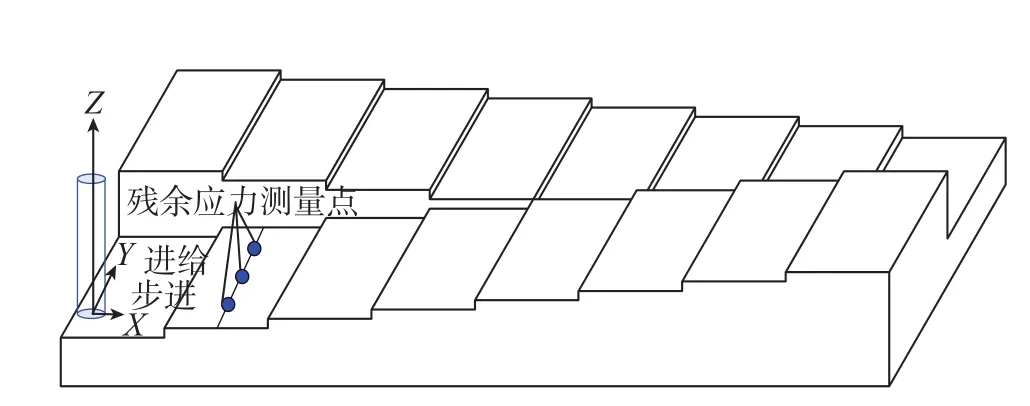
图1 试验方案及测量点示意图Fig.1 Experiment plan and measurement points

2 铣削试验结果分析

铣削加工表面存在残余应力的主要原因包括冷塑性变形、热塑性变形以及金相组织的变化，最终表面层的残余应力性质是上述3种原因综合作用的结果。尽管各加工区域对应不同的切削参数组合，但工件表面的残余应力均为压应力，这是由于切削速度较小，切削过程中虽未使用切削液，但切削温度并不高，而且大部分热量被切屑带走，热塑性变形较小，表面层温度也未达到相变点而发生金相组织转变，故而冷塑性变形占主导地位。

2.1 铣削速度-残余应力的关系

从残余应力随铣削速度的变化曲线（图2）可以看出：当切削速度从20m/min升高到35m/min时，X向残余压应力从718.66MPa降至665.88MPa，这是因为随着切削速度的提高，切削力减小而切削温度升高，导致冷塑性变形程度下降。当铣削速度超过35m/min时，切削温度继续升高，尽管切削力增大增强了冷塑性变形作用效果，但不如切削温度作用效果明显，热塑性变形抵消一部分残余压应力，因此步进方向的残余压应力值变小，但此时仍然是冷塑性变形占主导地位。

2.2 每齿进给量-残余应力的关系

分析残余应力随每齿进给量的变化曲线（图3）可知：当每齿进给量在0.02～0.06mm/z区间内增大时，金属切除率增加，切削力增大，单位时间产生的热量增多，导致热塑性变形作用增强，因此残余压应力水平降低。当每齿进给量在0.06～0.08mm/z变化时，由于刀具移动速度加快，切削热作用于工件表面的时间缩短，热塑性变形作用下降，因而残余压应力水平有所提高。

表1 铣削参数及残余应力测量结果

2.3 铣削深度-残余应力的关系

图4为残余应力随铣削深度的变化曲线，分析可知，残余压应力水平呈先下降后上升趋势，说明热塑性变形的作用效果有所减弱。当铣削深度在0.4～0.8mm变化时，尽管切削深度增加导致切削力增大（切削力在0.6～0.8mm区间内下降幅度很小，可认为切削力大小基本保持同一水平），单位时间产生的切削热增多，但刀具-工件接触区域增大，切削刃工作长度增长，有效改善了散热条件，削弱了切削热热塑性变形的作用效果，因而残余压应力增大。

2.4 铣削宽度-残余应力的关系

残余应力随铣削宽度的变化曲线如图5所示，分析可知，当铣削宽度在0.4～0.8mm变化时，残余应力随铣削宽度增大的变化情况与铣削深度基本类似。随着切削宽度的增大，同时参与切削工作的刀具齿数增多，导致切削力增大，与此同时单位时间产生的切削热增多，切削温度升高，但刀具-工件接触面积增大，同样有效地改善了散热条件，从而削弱了切削热热塑性变形的作用效果，因而残余压应力较0.4mm时均增大。此外，残余应力值总体变化幅度不大，说明切削宽度并不是影响残余应力大小的重要因素。

3 灵敏度分析及参数优选

为了减小各设计变量量纲的不同对残余应力灵敏度分析的影响，对各工艺因素进行归一化处理：

归一化处理后残余应力的变化规律如图6所示。分别对试验结果中4条残余应力变化曲线进行拟合，构建切削速度-残余应力、每齿进给量-残余应力、轴向切深-残余应力、径向切深-残余应力的数学模型为：

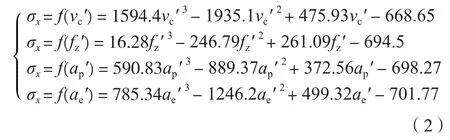
设目标函数为f(x)，设计变量为x，其中x=（x1，x2，x3，…，xn），n代表试验因素的个数，若f(x)可导，则灵敏度S可表示为：

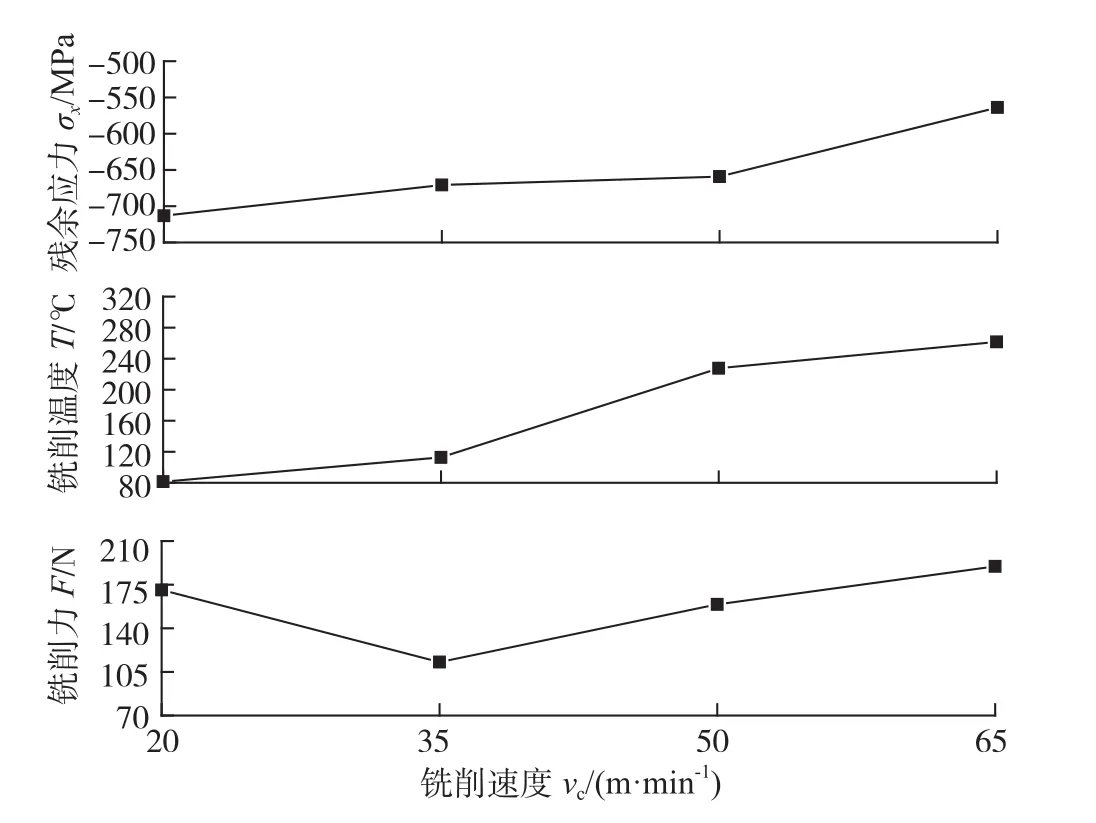
图2 铣削速度-残余应力曲线Fig.2 Variation of residual stress with milling speed

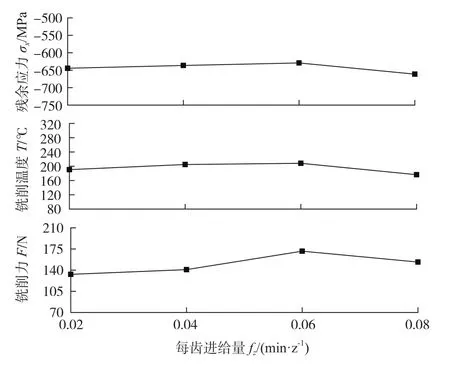
图3 每齿进给量-残余应力曲线Fig.3 Variation of residual stress with feed per tooth

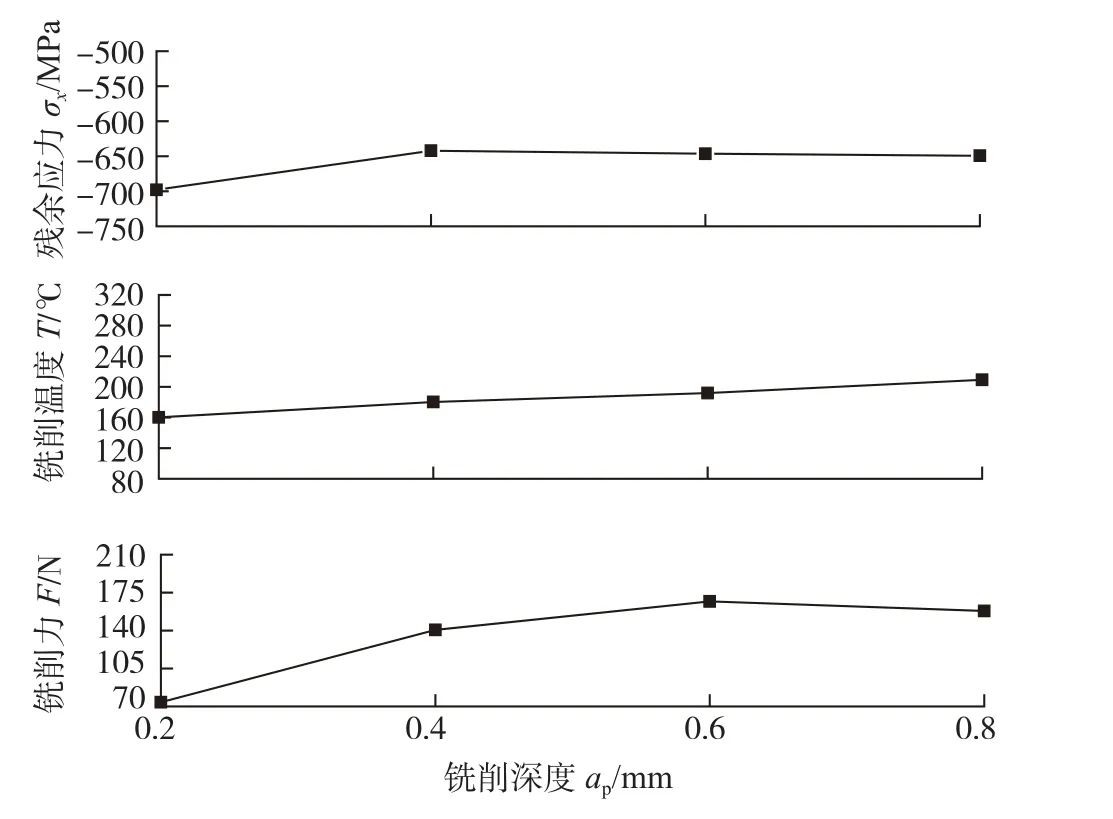
图4 铣削深度-残余应力曲线Fig.4 Variation of residual stress with milling depth

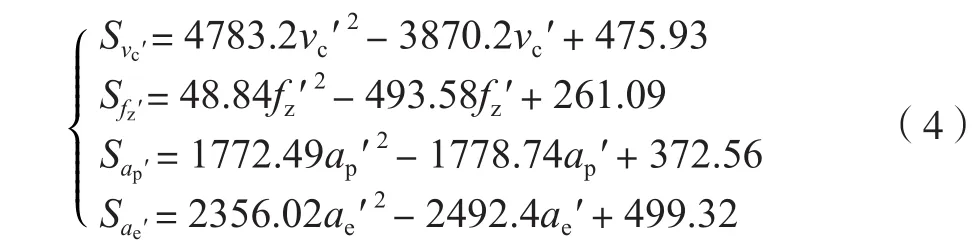
灵敏度绝对值的平均值是衡量设计目标对设计变量敏感强弱程度的标准，计算方法是对公式（4）中的二次函数取绝对值随后进行积分，积分区间为[0,1]，从而得出随着切削速度的变化，灵敏度绝对值的平均值为342.57，表明残余应力对铣削速度在试验参数范围内变化时最敏感；其次是铣削深度，其灵敏度绝对值的平均值为149.49；再次是径向切深，其灵敏度绝对值的平均值为114.09；最后为每齿进给量，灵敏度绝对值的平均值为112.77。由于铣削深度、铣削宽度和每齿进给量3者的灵敏度值相差不大，故可认为残余应力对此3者变化时的敏感程度近似相同。此外，图7为灵敏度数学模型的曲线，可以看出，较小的灵敏度数值，意味着残余应力变化不大，若设定灵敏度数值范围为 ±100，则vc'∈ (0.113,0.197)∪ (0.613,0.696)，fz'∈ (0.338,0.794)，ap'∈ (0.189,0.815)，ae'∈(0.197,0.397)∪(0.688,0.861)， 也即vc∈ (25.09,28.87)∪ (47.59,51.32)，fz∈ (0.04,0.06)，ap∈ (0.31,0.69)，ae∈ (0.32,0.44)∪ (0.61,0.72)。若以获得较大残余压应力为优化目标，应优先对切削速度进行选择并保证灵敏度值在负值区域（灵敏度为负值表示残余压应力增大），因此选择切削速度为50m/min，然后对每齿进给量进行选择，可确定为0.06mm/z，最后对轴向切深和径向切深进行选择，可确定为ap=0.6mm，ae=0.4mm，因此较优的切削参数组合为vc=50m/min，fz=0.06mm/z，ap=0.6mm，ae=0.4mm。

4 结论

基于X射线衍射技术，研究了铣削速度-残余应力、每齿进给量-残余应力、铣削深度-残余应力及铣削宽度-残余应力的影响关系，在试验参数范围内，可以得到以下结论：

（1）工件表面X向残余应力均为残余压应力，这是由于冷塑性变形占主导地位。

（2）建立了不同切削参数对表面残余应力的数学模型，通过切削参数的灵敏度分析，发现残余应力对切削速度的变化最敏感，对每齿进给量、铣削深度和铣削宽度的敏感程度近似相同。

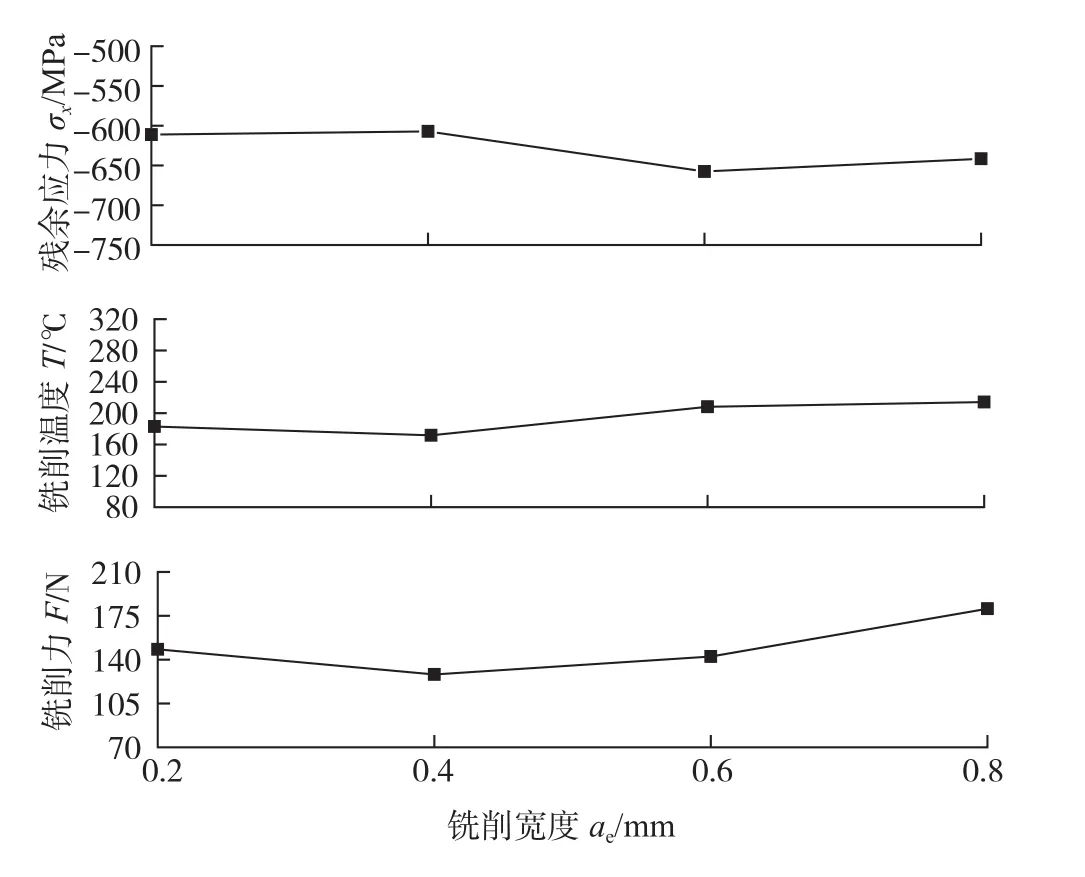
图5 铣削宽度-残余应力曲线Fig.5 Variation of residual stress with milling width

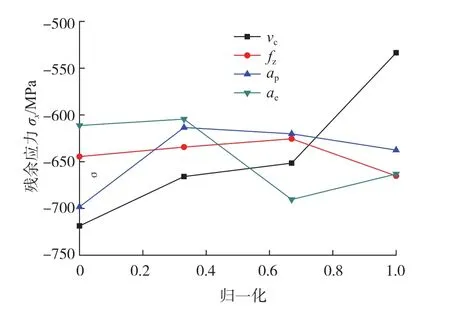
图6 归一化参数-残余应力曲线Fig.6 Variation of residual stress with normalized cutting parameters

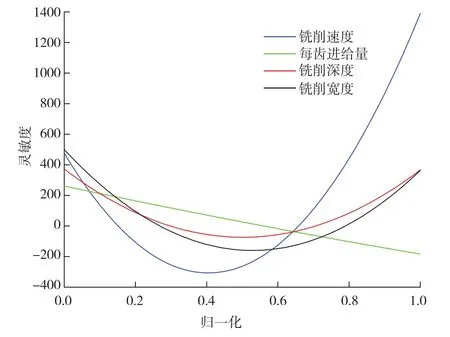
图7 残余应力灵敏度曲线Fig.7 Sensitivity curve of residual stress

（3）以获得较大残余压应力为优化目标，较优的切削参数组合为vc=50m/min，fz=0.06mm/z，ap=0.6 mm，ae=0.4mm。

参 考 文 献

[1] C.莱茵斯，M.皮特尔斯. 钛与钛合金[M].陈振华，译.北京：化学工业出版社，2005:79-83.

LEYENS C, PETERS M. Titanium and titanium alloys[M]. CHEN Zhenhua, tran. Beijing: Chemical Industry Press, 2005:79-83.

[2] BERANOAGIRRE A, LACALLE L N L D. Turning of gamma TiAl intermetallic alloys[J]. AIP Conference Proceedings, 2012,1431(80):526-532.

[3] SHARMAN A R C. Workpiece surface integrity considerations when finish turning gamma titanium aluminide[J]. Wear, 2001, 249:473-481.

[4] PRIARONE P C, RIZZUTI S, ROTELLA G, et al. Tool wear and surface quality in milling of a gamma-TiAl intermetallic[J].The International Journal of Advanced Manufacturing Technology,2012,61(1):25-31.

[5] 陈建岭，李剑锋，孙杰. 钛合金铣削加工表面残余应力研究[J].机械强度，2010, 32(1): 53-57.

CHEN Jianling, LI Jianfeng, SUN Jie. Surface residual stress of titanium alloy induced by milling[J]. Mechanical Strength, 2010,32(1):53-57.

[6] MANTLE A L, ASPINWALL D K. Surface integrity of a high speed milled gamma titanium aluminide[J]. Journal of Materials Processing Technology, 2001, 118(1-3): 143-150.

[7] MANTLE A L, ASPINWALL D K. Cutting force evaluation when high speed end milling a gamma titanium aluminideintermetallic alloy[J].Intermetallics and Superalloy, 2006, 10:209-215.

[8] HOOD R, ASPINWALL D K, SOO S L, et al. Workpiece surface integrity when slot milling γ-TiAl intermetallic alloy[J]. CIRP Annals-Manufacturing Technology, 2014, 63(1):53-56.

[9] 田荣鑫，姚倡锋，黄新春，等.面向加工表面粗糙度的钛合金高速铣削工艺参数区间敏感性及优选[J].航空学报，2010，31(12):2464-2470.

TIAN Rongxin, YAO Changfeng, HUANG Xinchun, et al. Process parameter interval sensitivity and optimization of machined surface roughness for high-speed milling of titanium alloys[J]. Acta Aeronautica et Astronautica Sinica, 2010,31(12):2464-2470.

[10] 刘振学，黄仁和，田爱民. 实验设计与数据处理[M].北京：化学工业出版社，2005:62-67.

LIU Zhenxue, HUANG Renhe, TIAN Aimin. Experimentaldesign and data processing[M]. Beijing: Chemical Industry Press, 2005:62-67.