34CrNiMo6钢复合喷丸强化的有限元模拟*

梁 若，庞思勤，程冠华，张 磊，项俊锋，白 龙，陈建军，解丽静

（1.北京理工大学机械与车辆学院，北京 100018;2.山西柴油机工业有限责任公司，大同 037000）

喷丸强化是航空、航天、车辆等领域广泛应用的表面强化手段之一。其强化原理是通过大量球形（或近似球形）弹丸轰击待加工的零件表面，使其发生塑性变形，形成残余压应力，从而显著提高材料的疲劳性能、表面强度、抗应力腐蚀性能等[1]。在实际生产中，复合喷丸是处理工件常用的一种方式，可在工件表面获得更高的残余应力及更好的表面质量。复合喷丸工艺一般顺序为先采用大尺寸的弹丸进行高强度喷丸（第一步喷丸），再采用小尺寸的弹丸进行低强度喷丸（第二步喷丸）。若仅用一种弹丸进行喷丸强化处理，则为单次喷丸。在目前的研究中，主要采用试验的方法对复合喷丸所产生的残余应力进行研究[2-4]，但对复合喷丸进行有限元仿真分析却不多见。

由于喷丸工艺参数较多，目前几乎没有对喷丸在不同工艺参数下强化效果变化规律的系统试验研究，而多采用计算机仿真模拟快速得到不同工艺参数下残余应力场的变化规律。因此，有限元分析方法逐渐成为研究喷丸强化的重要手段之一。Klemenz等[5]研究了入射序列对喷丸残余应力的作用规律，并发现应力值在喷丸区域取平均值和试验结果更为接近。Miao等[6]建立了随机弹丸喷丸模型，讨论了两种入射角度下残余应力的变化规律。李源等[7]模拟了多弹丸随机入射Q235钢板的过程，并与单弹丸模型模拟结果作比较，发现多弹丸模型能够更好地模拟实际的喷丸强化。

目前，关于喷丸的有限元仿真多集中在单次喷丸弹丸阵列的排布方式上，其研究相对较完善。而关于复合喷丸强化的有限元模型模拟的文献较少，且复合喷丸因其更好的强化效果和表面质量而被广泛应用于实际生产中。鉴于此，本文采用有限元分析软件ABAQUS对34CrNiMo6钢复合喷丸强化过程进行数值模拟，提出了随机弹丸周期性模型，分析了复合喷丸强化残余应力场的分布规律，以及第二步喷丸的喷丸（阿尔门）强度对复合喷丸强化效果的影响。

1 周期性有限元模型

1.1 相邻弹丸间距的确定

在实际的喷丸过程中，大量弹丸无规律地随机撞击靶材，直接模拟这个物理过程十分困难。本文引入周期性模型的思想，以较小面积的代表单元来模拟实际情况中大面积工件表面的工况。因此，为保证所模拟的单元具有代表性，需将杂乱的弹丸排列成阵列，如图1所示。Gari é py等[8]利用高速摄像机研究实际喷丸过程中弹丸的分布情况，结果表明大多数弹丸是先后撞击靶材的，在极少数两颗弹丸几乎同时撞击靶材的情况中，弹丸之间也有较大的距离，可以认为弹丸之间互相没有影响。因此，只要相邻弹丸之间有一定距离使弹丸无相互影响，就可将弹丸流按周期性排列来进行模拟。

为研究弹丸间距对相邻弹丸形成应力的影响规律，建立了双弹丸模型，如图2所示。模型中，两粒弹丸的水平中心距为C，第一粒弹丸冲击靶材后会在A-A线沿深度方向上形成残余应力σ；随后第二粒弹丸的冲击会使A-A线上的残余应力分布发生改变Δσ。图3给出了C和Δσ的关系。从图3可知，随着弹丸水平中心距C的增大，后入射弹丸引起的A-A线上应力变化Δσ已经逐渐减小。当C≥2.5R时，应力变化和残余应力值相比已经可以忽略。因此，可认为靶材表面的某一点沿深度的应力分布不受与之相距为2.5R或2.5R以上的弹丸冲击的影响，故将相邻弹丸之间距离定为2.5R。

1.2 材料的本构模型

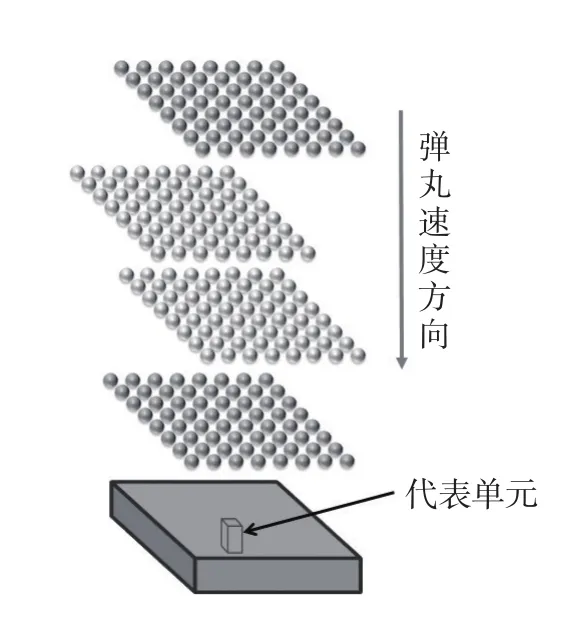
图1 周期性模型示意图Fig.1 Illustration of periodic model

喷丸靶材材料为34CrNiMo6钢，其本构关系描述选用Johnson-Cook本构模型，该模型能准确模拟喷丸时在高应变速率下材料的塑性变形。喷丸作为一种冷加工工艺，温度对材料塑性变形的影响可忽略不计。因此，其J-C本构模型可简化为：

其中，为材料等效塑性应力，为材料等效塑性应变，A为材料的屈服强度（MPa），B为材料的应变硬化常数，C、n、m为材料常数（通过材料力学性能试验测算得出），为应变率，为参考应变率，一般为1。表1列出了34CrNiMo6的相关J-C本构参数。

1.3 模型的建立

图2 双弹丸有限元模型Fig.2 Finite element model of double shots

图3 不同中心距C对相邻弹丸应力相互作用的影响Fig.3 Influence of different C values on the residual stress of adjacent shots

建立周期性模型的目的是用较小的单元来代表大面积的靶材区域，理想状态下代表单元可拼接为大面积的靶材区域，即代表单元具有周期性。在代表单元区域内随机位置生成一颗弹丸，在该弹丸周边相应生成8颗弹丸，相邻弹丸间距为2.5R，使弹丸之间无相互应力影响。球心位于代表单元区域内的弹丸为母球，其周边8颗弹丸为子球。母球位置是随机生成的，8颗子球的位置根据母球位置确定，子球的其他参数（半径、速度、材料等）均与母球相同。以弹丸半径R=0.6mm的情况为例，靶材模型X-Y平面的区域划分示意图如图4（a）所示，其中实线圆代表母球，虚线圆代表子球。区域1是应力检测区，考虑到仿真结果与试验结果的对照，该区域尺寸定为1mm×1mm，即X射线应力检测仪的最小测量范围。区域2是代表单元区域，也是随机生成母球球心位置的区域，母球在三维空间中位置的随机分布由ABAQUS/PYTHON脚本控制。区域3为子球球心所在的区域。为了保证代表单元具有周期性，区域2的尺寸为2.5R×2.5R，区域3的边长即为7.5R×7.5R。区域4是靶材模型的边界，尺寸为9.5R×9.5R。靶材模型高度为5R，可避免底部边界对应力场的影响。为节约计算成本，靶材模型区域2网格划分较密，采用8结点减缩积分C3D8R单元类型，其他区域网格较粗。弹丸材料为铸钢，在仿真中近似为解析刚体。

第N个母球球心（x,y,z）在空间的分布表示为：

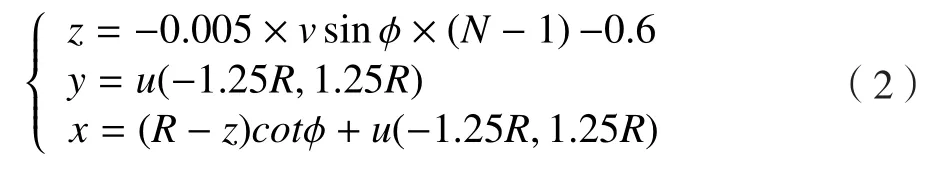
式中，v为喷丸速度，ϕ为入射角度，u（-1.25R, 1.25R）表示满足（-1.25R, 1.25R）之间均匀分布的随机数。每组弹丸入射间隔时间为5μs ，上一组弹丸撞击靶材所引起的应力振荡在此时间间隔内可大幅减弱[8]。以弹丸半径0.6mm，入射角度60°为例，周期性有限元模型如图4（b）所示。

2 模型验证

2.1 周期性验证

若代表单元具有周期性，可拼接成大面积的靶材，则代表单元相对的侧面上的应力分布应该是对称的。以弹丸半径0.6mm、喷丸速度40m/s、入射角度70°、母球数量50为例（按Miao等[6]提出的方法计算出当母球数量为50时代表单元的喷丸覆盖率可达到100%），验证模型的周期性，仿真结果如图5所示。在仿真开始和结束阶段，代表单元相对侧面的应力云图都体现出了良好的对称性，即面DD'A'A与面BB'C'C、面AA'B'B与面CC'D'D上的应力分布对称，这验证了该模型周期性的正确性。应力云图中细微的差别可能是由于代表单元区域网格划分较细而周边区域网格较粗引起的。

2.2 试验验证

为了验证仿真结果的正确性，进行了相同工况下（弹丸半径为0.6mm，喷丸速度为40m/s，入射角度为70°）的喷丸试验研究。试验试样经过调质热处理和磨削后，表面存在50～80MPa的拉应力。试验使用的喷丸设备为Q3518抛丸机，叶轮线速度定为40m/s，喷丸时间为1min。应力检测设备为X-350A型X射线应力测定仪，电解抛光设备为XF-1型电解抛光机，电解溶液为饱和NaCl溶液，每次抛光去除材料厚度为60～80μ m，去除厚度由Mitutoyo数显千分尺测定。

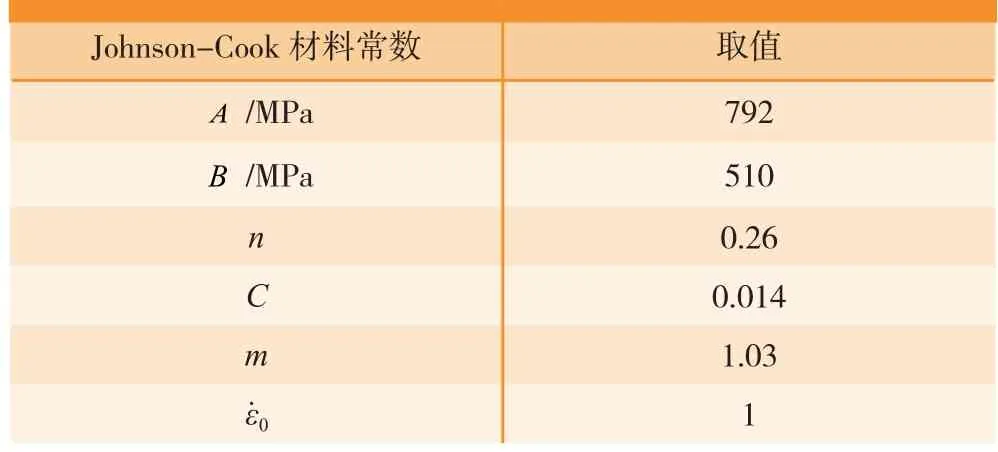
表1 34CrNiMo6材料Johnson-Cook参数

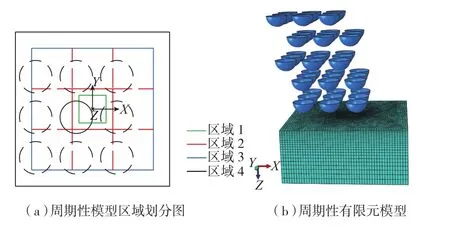
图4 周期性模型Fig.4 Periodic model

实际测量残余应力使用的X射线衍射与电解抛光法本身虽不会引入新的残余应力，但是电解抛光会去除表层材料，这在一定程度上破坏了靶材试样原有的应力平衡，引起喷丸残余应力的重新分布，因此采用ABAQUS的Model Change技术模拟电解抛光的过程。Model Change方法可以将原有模型中部分几何元素或网格在指定的分析步中无效化，这一过程和电解抛光一样不会引入新的应力，所以成为了模拟电解抛光过程的有效手段。试验结果与仿真结果如图6所示。残余应力场分布呈现出相同的变化趋势，喷丸试验和仿真均在材料表面引入了残余压应力，随着深度的增加,残余压应力表现为先增加后减小的规律，这验证了周期性模型的正确性。仿真获得的最大残余压应力比试验值大，这可能与试样表面存在的初始残余拉应力有关。

3 利用周期性模型模拟复合喷丸

3.1 比较复合喷丸与单次喷丸

图5 代表单元的应力分布Fig.5 Stress distribution of representative cell

在本文的复合喷丸仿真模型中，所有的弹丸都近似为刚体，材料均为铸钢，但第二步喷丸的弹丸半径较小。仿真模型的相关喷丸参数如表2所示。其中模型1是单次喷丸，弹丸半径为0.6mm，覆盖率为100%；模型3为复合喷丸，两步喷丸的弹丸半径分别为0.6mm、0.3mm，覆盖率均为100%；模型2是模型3的对照组。为了保证模型的周期性，模型3中小弹丸的排列方式按1.3节中的周期规则进行了调整。模型3的弹丸排列如图7所示。

图8所示为复合喷丸残余应力的仿真结果。可以看出，模型1和模型3最大残余应力所处的深度相同，均为0.195mm，但在0～0.195mm深度范围中模型3的残余应力均大于模型1。此结果与Fu等[9]的复合喷丸试验结果类似，进一步说明了周期性模型的正确性。模型2与模型3覆盖率相同，但因第二步喷丸中弹丸尺寸的不同，残余应力场分布不同。在模型2中，层深较大处残余应力大于模型1，但在较浅的层深中残余应力与模型1相近甚至更小。对比3个仿真结果，可以得出结论，复合喷丸在浅表面所形成的残余应力比单次喷丸所形成的残余应力大。

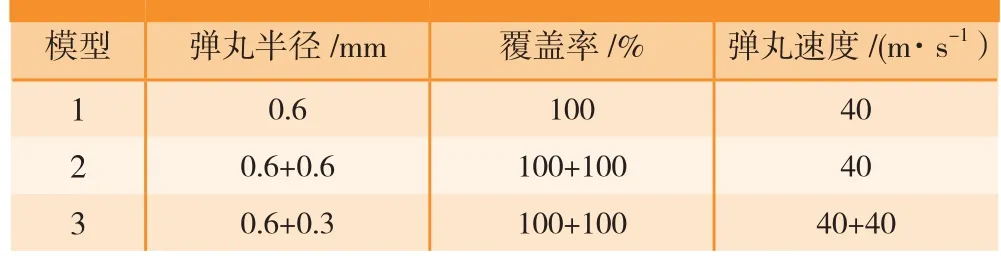
表2 单次喷丸及复合喷丸仿真模型参数

图6 试验结果与仿真结果的对比Fig.6 Comparison of residual stress profiles obtained by experiment and simulation

图7 复合喷丸的弹丸排列示意图Fig.7 Shots array schematic diagram of dual peening

图9所示为模型1和模型3中代表单元表面的残余应力云图。模型1和模型3表面S11的标准差分别为390.11MPa和345.98MPa。通过比较应力云图和S11的标准差，可以看出复合喷丸可以得到更均匀的表面应力分布。模型1和模型3的表面粗糙度为：

式中，zi（i=1,2,…，n）是模型表面第i个节点的垂直位移，N是所计算的节点个数。为了得到更准确的结果，靶材表面区域2中所有的节点的垂直位移都进行了计算。得到的结果为模型1表面粗糙度为Ra=8.8μm，模型3表面粗糙度为Ra=8.0μm。这说明复合喷丸可以形成更好的表面质量。

3.2 喷丸强度对复合喷丸的影响

在很多关于复合喷丸的研究中，喷丸（阿尔门）强度是区分两步喷丸的重要参数。Miao等[10]研究表明，喷丸强度与入射速度呈正相关关系，并且入射速度是影响喷丸强度的主要参数。因此可以将入射速度作为变量来研究喷丸强度对复合喷丸的影响。表3所示为模型3、4、5的喷丸参数，图10为残余应力的仿真结果。

图8 模型1～3的残余应力分布Fig.8 Residual stress distribution of model 1～3

图9 代表单元表面的应力分布Fig.9 Residual stress distribution of representative cell

表3 复合喷丸仿真模型参数

图10 模型1～5的残余应力分布Fig.10 Residual stress distribution of Model 1～5

从图10中可以看出，模型1～5中残余应力最大值均在0.195mm处，且随着第二步喷丸的入射速度即喷丸强度的增加，0～0.195mm深度的残余应力先增大后减小，层深大于0.272mm后残余应力值基本相同。模型4和5中0～0.195mm深度的残余应力比模型1中小，这可能是由于喷丸强度过大而造成过度喷丸，使强化效果变差。

4 结论

（1）对于先后连续入射的弹丸，后入射的弹丸对先入射的弹丸残余应力场的影响随着弹丸间距的增加而减小。

（2）本文提出的周期性模型具有良好的周期性，而且仿真结果与试验结果相近，因此该模型可用于模拟随机多弹丸入射的喷丸强化。

（3）复合喷丸相对于单次喷丸可在靶材表面形成更均匀的残余应力场，而且可在浅表面形成更大的残余压应力。

参 考 文 献

[1] SHIGERU H, HIYOKAZU S. Studies on improvement of surface durability of carbonitrided and hardened gear steel[J]. Journal of the Japan Society for Precision Engineering, 2000, 66(11):1766-1770.

[2] 李荣斌, 王相虎, 尚海龙, 等. 复合喷丸工艺对S30432钢表面应力与组织的影响[J]. 材料热处理技术, 2012, 41(4):148-149.

LI Rongbin, WANG Xianghu, SHANG Hailong, et al. Effect of composite shot peening on residual stress and microstructure of S30432 Steel[J]. Material & Heat Treatment, 2012, 41(4):148-149.

[3] 朱晨, 姜传海. 17Cr2Ni2Mo钢的表面复合喷丸强化[J]. 机械工程材料, 2011,35(9):98-99.

ZHU Chen, JIANG Chuanhai. Composite shot peening of 17Cr2Ni2Mo steel surface[J]. Materials for Mechanical Engineering,2011,35(9):98-99.

[4] ZHAN K, JIANG C H , WU X Y, et al. Surface layer characteristics of S30432 austenite stainless steel after shot peening[J]. The Japan Institute of Metals, 2012, 53(5):1002-1006.

[5] KLEMENZ M, SCHULZE V, VOHRINGER O, et al. Finite element simulation of the residual stress states after shot peening[J].Materials Science Forum, 2016, 524: 349-354.

[6] MIAO H, LAROSE S, PERRON C, et al. On the potential applications of a 3D random finite element model for the simulation of shot peening [J]. Advances in Engineering Software, 2009, 40(10): 1023-1038.

[7] 李源, 雷丽萍, 曾攀. 弹丸束喷丸有限元模型数值模拟及试验研究[J]. 机械工程学报, 2011, 47(22): 43-48.

LI Yuan, LEI Liping, ZENG Pan. Shot stream finite element model for shot peening numerical simulation and its experiment study[J]. Journal of Mechanical Engineering, 2011, 47(22): 43-48.

[8] GARIÉPY A, LAROSE S, PERRON C, et al. Shot peening and peen forming finite element modelling-towards a quantitative method[J].International Journal of Solids and Structures, 2011, 48(20):2859-2877.

[9] FU P, ZHAN K, JIANG C. Micro-structure and surface layer properties of 18CrNiMo7-6 steel after multistep shot peening[J]. Materials and Design, 2013, 51(5):309-314.

[10] MIAO H Y, LAROSE S, PERRON C, et al. An analytical approach to relate shot peening parameters to almen intensity[J]. Surface &Coatings Technology, 2010, 205(7):2055-2066.