主动配电网三相电压优化及校正控制方法

董 雷 ，明 捷 ，蒲天骄 ，于 汀 ，崔 琳 ，周建华

（1.华北电力大学 新能源电力系统国家重点实验室，北京 102206；2.中国电力科学研究院，北京 100192；3.国网江苏省电力公司电力科学研究院，江苏 南京 210036）

0 引言

电压质量会影响电力系统的安全稳定运行。随着分布式电源的大量接入、用户与电网的双向互动、各种新型可控单元的广泛应用，配电网主动性日渐增强，传统的配电网运行理论不再完全适用［1-2］。因此，需要深入研究主动配电网的电压优化与校正控制技术，达到节能降损、提高电压质量及能源利用效率等目的。

目前对主动配电网电压优化控制问题的研究常常只考虑单相模型。由于中低压配电网中线路不再三相整体循环换位，且存在三相不对称供电的情况，电网优化控制应基于三相模型进行分析决策，以真实反映电网的运行状态，满足各三相独立可调设备的调节需要。文献［3］基于三相模型分析了单相并网的分布式电源与节点电压的灵敏度关系，揭示出单相模型下难以发现的多分布式电源相间耦合现象。文献［4-5］均对三相主动配电网优化控制的求解策略展开了讨论。与此同时，众多文献提出了含有分布式电源的无功优化方法［6-7］，然而由于配电网络线路R/X过大，需要考虑有功和无功的联合控制。文献［8］为提高分布式电源并网能力及控制节点电压水平，提出了单相模型的有功无功联合控制策略。

由于全网优化控制周期较长，而分布式电源的强随机性以及负荷的动态变化特性使得配电网电压幅值波动越来越明显，单纯依靠全网优化控制无法使电网始终维持在最优运行状态，需要在电网局部通过可调节的分布式电源、无功设备的协调控制，快速校正电网波动。文献［9-10］采用内点法对电压进行校正控制，但内点法处理三相网络时速度较慢。同时，配电网中存在的单相负荷以及低压配电网中存在的非全相接入的分布式电源使配电网三相不平衡度更加严重，导致三相电压不对称、中性点电位位移、线路损耗增大等一系列问题［11-12］，对电压质量的威胁日益严重。国家标准GB/T15543—2008《电能质量三相电压不平衡》对电压不平衡度的允许值等做了相关规定。而目前电压校正控制方法一般仅仅局限于控制电压幅值在一定范围，较少考虑对节点电压三相幅值、相角差的控制［13-14］。

针对上述问题，本文提出一种基于多时间尺度的主动配电网有功无功协调的三相电压优化及电压相量校正控制方法。在长周期内，协调全网有功和无功资源，基于半定规划理论建立计及本支路相间互感的三相主动配电网无功优化的数学模型，实现全网优化控制。在短周期内，利用电压相量对节点注入功率的三相灵敏度建立电压相量校正二次规划模型，实现电压相量校正控制。

1 协调控制体系架构

根据国家电网公司《智能电网调度技术支持系统》系列标准中的规定，电网优化控制周期不超过5 min，控制周期为分钟层级，属于实时控制范畴。尽管如此，由于负荷波动、分布式电源的强随机性等原因，分钟层级的电压控制仍然无法可靠地保证电压平稳持续地处于规定范围内，需要在短时间内利用尽可能小的功率调整量对越限节点电压实现快速校正。为此，本文建立三相主动配电网的电压优化模型并提出电压控制策略，按时间尺度提出了分钟层电压优化控制和秒层电压相量校正控制的两级控制体系架构，如图1所示。

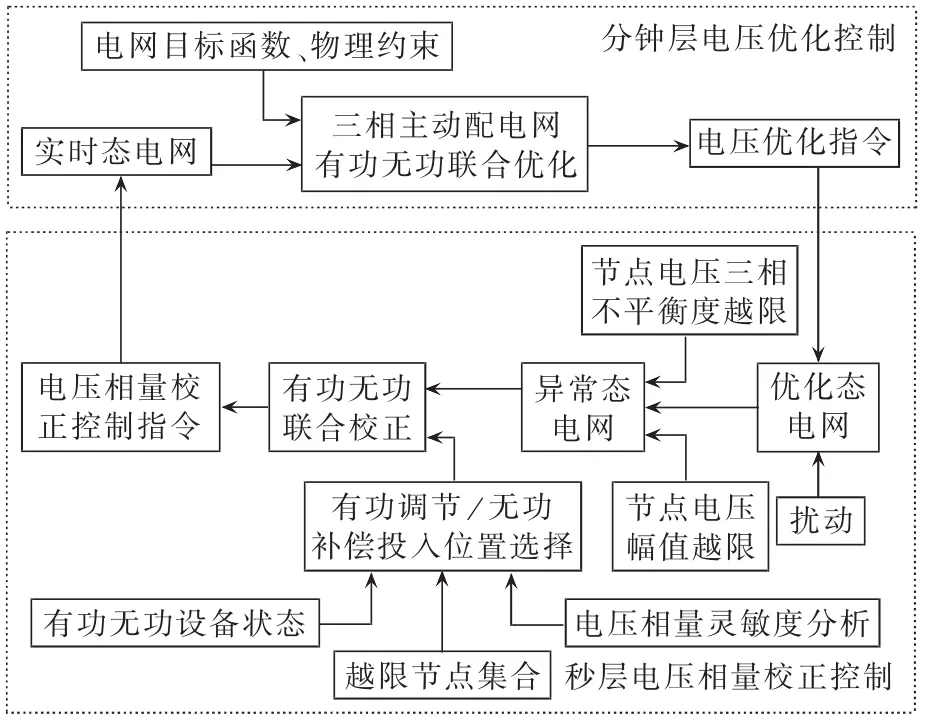
图1 协调控制体系架构Fig.1 Structure of coordinated control system

该协调控制体系架构总体思路是在分钟层级进行三相主动配电网电压优化建模，周期性地进行有功无功联合优化计算；而在秒层级内周期性地监视优化后电网运行状态，检测电压幅值越限节点及三相不平衡度越限节点，并在发现上述节点时进行有功无功协调的电压相量校正控制，以保证电压平稳持续地处于要求范围内，提高电压质量。2个层级的具体实现方法如下。

分钟层级：采用电网优化控制周期，每5 min进行一次优化计算。针对三相主动配电网建立有功无功联合电压优化模型，进行全网电压优化计算，跟踪负荷趋势性变化，调节各有功/无功源的输出功率，使电网运行于最优潮流状态。

秒层级：考虑分布式电源及负荷快速波动等情况，每10～20s进行一次校正计算。在电网运行于优化状态后，监视由于扰动（如分布式电源和负荷变化等）引起的电网状态量的改变。其主要监视的对象为节点电压幅值和节点三相电压幅值差、相角差。当上述变量超过允许运行范围时，则进行电压相量校正控制，在实现将状态量控制在合理运行范围内的同时，避免引起新的状态量越限。本层级的电压校正控制机制在传统的电压校正控制方法上进行改进，可以在快速校正越限节点电压幅值的同时减少三相不平衡度，保证电压质量。为了实现全网电压潮流的平稳过渡，校正过程中将利用尽量小的功率调整量，对影响越限节点电压较大的有功/无功源进行局部电压校正控制。

2 分钟层全网优化控制

2.1 目标函数

选择配电网有功网损最小作为目标函数。即所有节点的注入有功功率之和最小：

其中，n为系统节点数；φ 表示 A、B、C 三相；PLoss为系统有功网损为系统中节点i的注入功率。

2.2 约束条件

（1）平衡节点约束。

本文针对三相网络进行建模，需要在约束条件中固定平衡节点的三相相角，以反映电网的实际情况，即：

其中为平衡节点的φ相电压相量。

（2）潮流平衡约束。

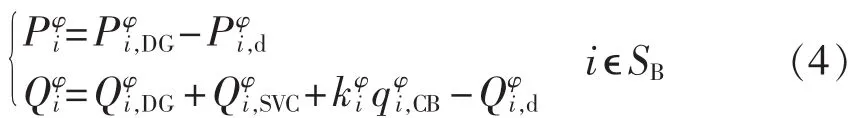
其中为节点 i上所连接的分布式电源的有功出力和分别为节点 i上所连接的分布式电源的无功出力、静止无功补偿器（SVC）的无功补偿功率以及无功负荷；为分组投切电容器组的档位为分组投切电容器组单位档位的无功补偿功率；SB为系统中所有节点的集合。

（3）连续控制变量约束。

其中，分别为分布式电源可调有功出力的下限值和上限值；和和分别为分布式电源、SVC可调无功出力的下限值和上限值；SDG和SSVC分别为分布式电源和SVC所在节点的集合。主动配电网中可控分布式有功电源包括内燃机、燃气轮机等，而风电、光伏等分布式电源通常运行在最大出力跟踪状态，将其视为不可控的有功电源，只作为可控的无功电源使用。

（4）离散控制变量约束。

其中，为节点i所连接分组投切电容器组的最高档位；SCB为电容器组所在节点的集合。

（5）状态变量约束。

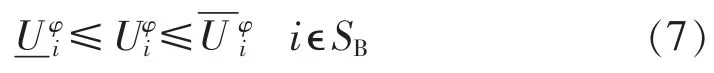
其中，分别为节点i的φ相电压幅值及其下限值、上限值。

综上建立的优化模型是一个非凸非线性混合整数规划模型。考虑到凸规划模型能够保证解的全局最优性，本文采用半定松弛的方法将所建模型松弛为一个凸的半定规划（SDP）模型［15］。建立计及本支路相间互感的三相主动配电网电压优化模型如式（8）所示。

其中，为U的共轭转置；Y为计及本支路互感的三相网络节点导纳矩阵；为平衡节点约束对应的系数矩阵；tr（X）代表矩阵X的迹。 对于系数矩阵 Aj，当j=1，2，…，3n 时，Aj（1，j）=ej（-120°），Aj（2，j）=-1，Aj其余元素均为 0；当j=3n+1 ，3n+2，… ，6n 时，Aj（1，j）=ej120°，Aj（2，j） =-1，其余元素均为0。

3 秒层局部校正控制

为了实现全网电压潮流的平稳过渡，本文在保证可再生分布式电源有功出力最大的同时，采取局部校正控制的手段，通过灵敏度分析方法选取对越限节点电压相量影响最大的有功/无功源出力作为控制变量。同时，在约束条件中考虑节点电压三相幅值、相角差的限值，保证三相不平衡度处于一定范围内。

3.1 目标函数

局部校正选取的目标函数为功率调整量最小，即：

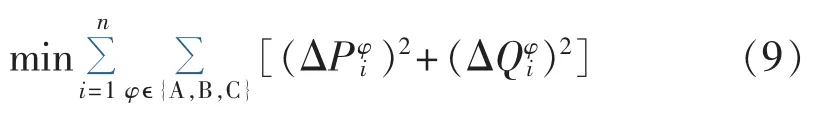
其中，和分别为节点 i的 φ 相注入有功功率和无功功率调整量。

3.2 约束条件

（1）节点电压约束。

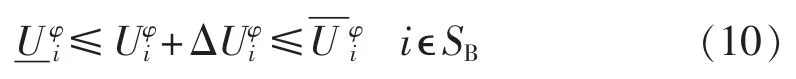
其中，为节点i的φ相电压幅值改变量。

（2）三相不平衡度约束。

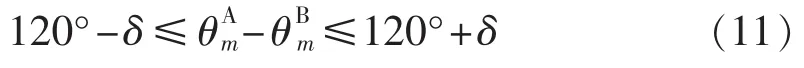
其中，分别为电压幅值、电压相角越限（三相不平衡度越限）节点m的φ相电压幅值、电压相角。

（3）潮流方程约束。

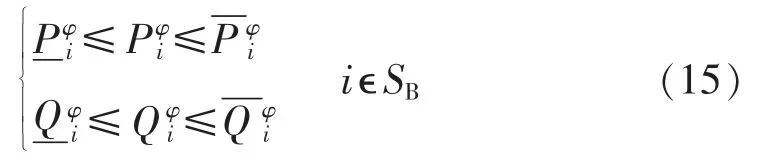
其中，

（4）离散控制变量约束。

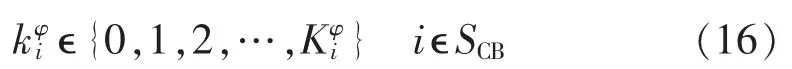
3.3 主动配电网电压对节点注入功率的三相灵敏度

对于具有n个节点的电力网络，其节点电压对节点注入功率的灵敏度关系式为：

其中，ΔUA，B，C、ΔθA，B，C、ΔPA，B，C和 ΔQA，B，C为 n-1 维列向量，分别表示节点电压幅值、节点电压相角、节点注入有功功率、节点注入无功功率的变化量；BA，B，C、GA，B，C分别为节点导纳矩阵的实部和虚部；PA，B，C、QA，B，C分别为以节点 i注入有功功率节点 i注入无功功率为对角元的对角矩阵。

3.4 模型转换及求解

为了便于描述，本文在不必要强调三相模型时忽略上角标φ以简化矩阵，将电压相量校正模型表示成矩阵形式，将式（17）所求结果代入式（9）—（16）中，得：

其中，T为对角元为2的对角阵；E为单位矩阵；、分别为以 120°-δ、120°+δ为元素的列向量；、分别为以-α、α为元素的列向量；δ、α分别为三相电压相角差允许偏差值、三相电压幅值差允许偏差值；分别为原 A、B、C、D 矩阵中仅保留三相不平衡度越限节点m对应的第m列、去掉其他列所组成的新矩阵。

本文采用局部电压校正控制的方法，通过灵敏度分析方法，找出节点注入有功功率、无功功率对每个电压幅值越限节点、三相不平衡度越限节点的电压相量的灵敏度较大的前3个有功/无功源，并设这些节点的集合为ST。考虑主动配电网中可控分布式有功电源包括内燃机、燃气轮机等装置；无功电源包括风电、光伏等分布式电源，SVC，分组投切电容器组等装置。由于大部分节点的节点注入功率是不可调的，其注入功率变化量为0。设节点注入有功功率可调节的节点的集合为SP，节点注入无功功率可调节的节点的集合为SQ。因此，对模型进行降阶处理，式（22）转化为：

其中，ΔP′为以 ΔPu为元素的列向量，uєST∩SP；ΔQ′为以 ΔQv为元素的列向量，vєST∩SQ；C′为 C 矩阵中仅保留节点注入有功功率可调、与待校正节点电压相量灵敏度大的节点u对应的第u列，去掉其他列所组成的新矩阵；D′为D矩阵中仅保留节点注入无功功率可调、与待校正节点电压相量灵敏度大的节点v对应的第v列，去掉其他列所组成的新矩阵；分别为中第 3j+1 列元素变为第3j+1列元素与第3j+2列元素之差、第3j+2列元素变为第3j+2列元素与第3j+3列元素之差、第3j+3列元素变为第3j+3列元素与第3j+1列元素之差所组成的新矩阵。

该模型为一个混合整数二次规划模型，可采用混合整数二次规划工具箱求解。

4 算法流程

5 min优化周期内的算法流程如下：

a.输入原始数据，包括电网参数、当前状态量、节点注入功率等，开始计时；

b.应用半定规划（SDP）法，使用SDP解工具箱求解三相主动配电网电压优化模型，得各节点电压Uφi；

c.根据式，得各有功/无功源输出功率，进而发出电压优化指令进行优化控制；

d.以10～20s为周期，监测电网状态，判断是否有节点电压幅值、节点电压三相幅值差、相角差越限，若未越限则等待下一校正周期，直至到达t=5min时刻，否则进行步骤e；

e.利用灵敏度分析方法，找出对越限节点电压影响较大的有功/无功源，将其发出功率作为控制量，确定有功调节/无功补偿位置；

f.采用混合整数二次规划工具箱求解式（23）所示电压相量校正控制模型，求出功率改变量ΔP′、ΔQ′，发出电压校正控制指令，调整各有功/无功源出力；

g.检测校正后各节点电压幅值各节点三相电压幅值差、相角差是否越限，若未越限则等待下一校正周期，否则进行步骤h；

h.输入当前数据，返回步骤c重新进行全网电压优化，开始下一优化周期。

5 算例分析

本文采用MATLAB-YALMIP平台在Lenovo-PC（i5-3210 CPU，4G RAM）上开发上述无功优化程序以验证本文所提方法的效果。操作系统为Win7 64bit，MATLAB版本为R2012a，YALMIP版本为20140605。混合整数二次规划工具箱版本为1.06。

5.1 IEEE 33节点系统电压优化测试算例

算例系统为改进的IEEE 33节点三相配电系统。其线路参数在文献［16］的基础上稍作修改，将节点21所连三相负荷（单位为kW、kvar）变为528+j162（A 相）、533+j165（B 相）、529+j163（C 相），其余各数据不变。在上述线路参数的基础上，增加2个光伏电源、2个内燃机、1个分组投切电容器组及1个SVC，如图2所示。

图2 改进IEEE 33节点算例系统图Fig.2 Modified IEEE 33-bus test system

具体参数如下：节点31连接分组投切电容器CB1，每组的补偿容量50kvar，总共10组；节点16连接有三相独立可调SVC，无功补偿区间为-100～300 kvar；电网额定电压为12.66 kV，所接分布式电源均为三相联动装置；节点6和节点23连接的内燃机有功调节范围为 0～650 kW、无功调节范围为 0～200 kvar；节点19所连接分布式光伏电源的有功出力限制在最大跟踪点处，为500 kW，无功调节范围为-50～250 kvar；节点21所连接分布式光伏电源的有功出力限制在最大跟踪点处，为1 000 kW，无功调节范围为-50～250 kvar。

5.2 全局优化的求解结果

针对5.1节中算例，建立三相主动配电网有功无功联合电压优化模型并采用MOSEK软件进行求解，并用原始-对偶内点法求解原始非凸非线性规划模型。表1列出了分别采用上述2种模型获得的结果。通过优化结果可以看出2种模型所得的解是一致的，这说明SDP模型是足够精确的，且求解效率很高。

表2列出了单纯调节无功功率进行电压优化的结果，将其与表1结果进行对比，可以看出采用有功无功联合进行电压优化的结果较单纯调节无功功率进行电压优化的结果更优。

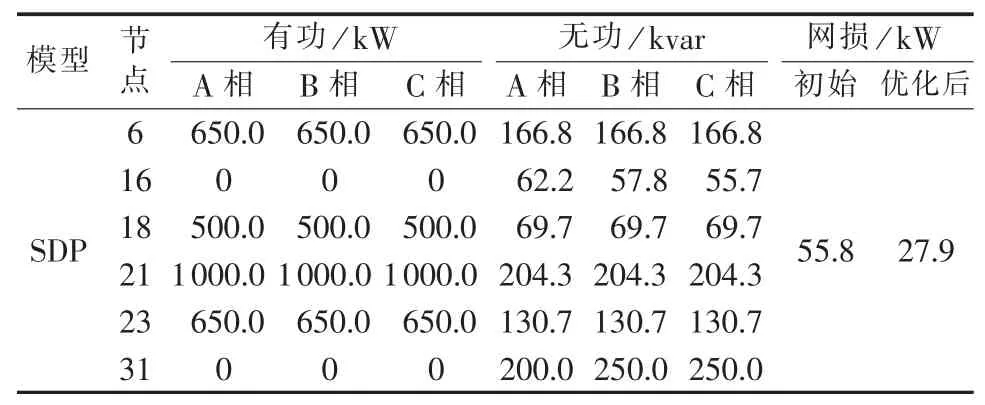
表2 单纯调节无功功率的电压优化结果Table2 Solutions of voltage optimization by adjusting reactive power only

将本文三相网络模型视为单相模型处理，即网络参数不变，通过增加SDP中约束条件实现电容器组三相联动，分布式电源、SVC等全相接入且调节量相同，重新进行电压优化，可以得到应用单相模型与三相模型的求解信息对照表如表3所示。结果显示建立三相模型进行电压优化，可以满足各相独立可调设备的调节需要，得到更精确的优化结果，进而达到更好的降损效果。

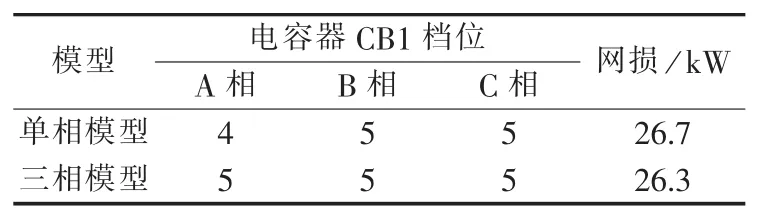
表3 用单相模型和三相模型的求解信息对照表Table3 Comparison of solutions between single-phase model and three-phase model

5.3 局部校正模型的求解

由于本时刻负荷快速波动等原因，电网将存在电压越限、三相不平衡度过大等现象，本文参考文献［17］将 1.042 UN、0.958 UN（UN为额定电压）作为电压警戒值，将±10%UN作为电压幅值差限值，将120°±1°作为相角差限值。假设本时刻节点21所连三相负荷（单位为 kW、kvar）变为 28+j12（A 相）、933+j169（B相）、929+j178（C相），其余各线路数据与5.1节所示算例数据相同，各有功/无功源发出功率如表1所示优化结果。此时电网的电压幅值及相角如表4所示，可以看到节点21的A相电压幅值为13.2008kV，超出1.042UN，电压幅值越限；三相电压幅值差未超过±10%UN，即 1.266 kV；三相电压相角差超过 120°±1°，不平衡度较大，超过限值。

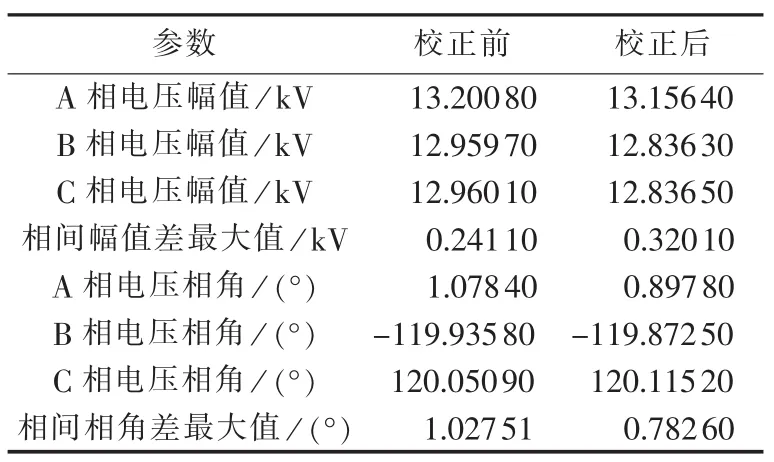
表4 校正前后电压幅值和相角Table4 Voltage magnitude and phase angle，before and after correction

首先求出影响节点21最大的3个有功/无功源，分别为节点18、21、23。应用本文方法求出上述3个节点的有功、无功补偿容量，结果见表5。

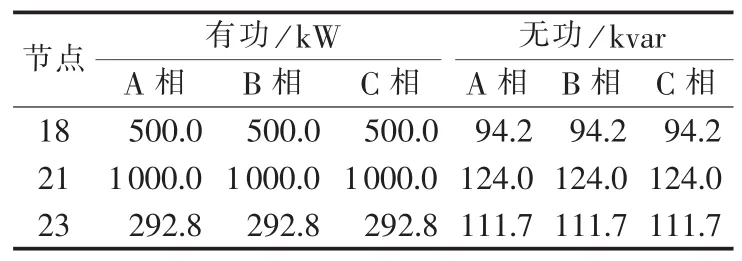
表5 校正模型的求解结果Table5 Solutions of correction model

校正后的电压幅值和相角见表4。可以看出，校正后电压幅值均在规定范围内，系统三相不平衡程度明显减小。

6 结论

a.在分钟级内，本文建立了计及本支路相间互感的三相主动配电网有功无功联合电压优化的数学模型，并采用SDP法求解，保证了解的全局最优性及快速收敛性。算例结果验证了本模型所求解的精确性及采用三相模型进行有功无功联合优化的必要性。

b.在秒级内，提出了节点电压相量对节点注入功率的三相灵敏度分析方法，建立电压相量校正二次规划模型，实现局部电压相量校正控制，结果表明本文方法能利用最小的功率调整量快速校正越限节点的电压幅值，并减少三相不平衡度。

本文工作在如下方面有待进一步扩展：考虑到主动配电网运行的经济性，如何权衡弃光与SVC、储能装置的经济性关系需要进一步考虑；同时，分布式电源的高渗透率下输电网和配电网的耦合关系不断增强，基于当前成果研究输配网协调的无功电压控制方法也是下一步的研究方向。

［1］于汀，刘广一，蒲天骄，等.计及柔性负荷的主动配电网多源协调优化控制［J］.电力系统自动化，2015，39（9）：95-100.YU Ting，LIU Guangyi，PU Tianjiao，et al.Multiple coordinated optimization control of active distribution network considering flexible load［J］.Automation of Electric Power Systems，2015，39（9）：95-100.

［2］李鹏，窦鹏冲，李雨薇，等.微电网技术在主动配电网中的应用［J］.电力自动化设备，2015，35（4）：8-16.LI Peng，DOU Pengchong，LI Yuwei，et al.Application of microgrid technology in active distribution network［J］.Electric Power Automation Equipment，2015，35（4）：8-16.

［3］FRANCO J F，RIDER M J，LAVORATO M，et al.Optimal conductor size selection and reconductoring in radial distribution systems using a mixed-integer LP approach［J］.IEEE Transactions on Power Systems，2013，28（1）：10-20.

［4］DESHMUKH S，NATARAJAN B，PAHWA A.Voltage/var control in distribution networks via reactive power injection through distributed generators［J］.IEEE Transactions on Smart Grid，2012，3（3）：1226-1234.

［5］BRUNO S，LAMONACA S，ROTONDO G，et al.Unbalanced three-phase optimal power flow for smart grids［J］.IEEE Transactions on Industrial Electronics，2011，58（10）：4504-4513.

［6］周冬旭，李晓明.面向电力市场的含风电机组配电网无功优化模型及其求解算法［J］.电力自动化设备，2013，33（4）：24-29.ZHOU Dongxu，LI Xiaoming.Reactive power optimization model and its algorithms for distribution system with wind farm in electricity market［J］.Automation of Electric Power Systems，2013，33（4）：24-29.

［7］段建东，杨杉.基于改进差分进化法的含双馈型风电场的配电网无功优化［J］.电力自动化设备，2013，33（11）：123-127，133.DUAN Jiandong，YANG Shan.Reactive power optimization based on modified differential evolution algorithm for power distribution system with DFIG wind farms［J］.Electric Power Automation Equipment，2013，33（11）：123-127，133.

［8］GABASH A，LI P.Active-reactive optimal power flow in distribution networks with embededded generation and battery storage［J］.IEEE Transactions on Power Systems，2012，27（4）：2026-2035.

［9］李亚男，张粒子，杨以涵，等.基于内点算法的电压校正控制［J］.电力系统自动化，2002，26（3）：28-31.LI Yanan，ZHANG Lizi，YANG Yihan，et al.Voltage corrective control based on interior point method［J］.Automation of Electric Power Systems，2002，26（3）：28-31.

［10］孙国强，任宾，卫志农，等.基于自适应加权预测-校正内点法的含VSC-HVDC电力系统最优潮流［J］.电力自动化设备，2015，35（3）：54-59.SUN Guoqiang，REN Bin，WEI Zhinong，et al.Optimal power flow of power system with VSC-HVDC based on AWPC-IPM［J］.Electric Power Automation Equipment，2015，35（3）：54-59.

［11］王代弟.配电网三相不平衡问题的分析与研究［D］.沈阳：沈阳工业大学，2007.WANG Daidi.Analysis and research of three-phase unbalance in distribution network［D］.Shenyang：Shenyang University of Technology，2007.

［12］王同勋，刘颖英，孙媛媛，等.三相不平衡扰动源的定位［J］.电力自动化设备，2015，35（9）：43-48.WANG Tongxun，LIU Yingying，SUN Yuanyuan，et al.Disturbance source locating for three-phase imblance［J］.Electric Power Automation Equipment，2015，35（9）：43-48.

［13］代飞，崔挺，徐箭，等.基于综合灵敏度分析的电压校正控制［J］.电力自动化设备，2011，31（12）：15-20.DAI Fei，CUI Ting，XU Jian，et al.Voltage correction control based on comprehensive sensitivity analysis［J］.Electric Power Automation Equipment，2011，31（12）：15-20.

［14］成煜，杭乃善.基于电网中枢点识别的无功电压控制分区方法［J］.电力自动化设备，2015，35（8）：45-52.CHENG Yu，HANG Naishan.Reactive voltage control partitioning based on power network pilot node identification［J］.Electric Power Automation Equipment，2015，35（8）：45-52.

［15］董雷，田爱忠，于汀，等.基于混合整数半定规划的含分布式电源配电网无功优化［J］.电力系统自动化，2015，39（21）：66-72.DONG Lei，TIAN Aizhong，YU Ting，et al.Reactive power optimization for distribution network with distributed generators based on mixed integer semi-definite programming［J］.Automation of Electric Power Systems，2015，39（21）：66-72.

［16］车仁飞，李仁俊.一种少环配电网三相潮流计算新方法［J］.中国电机工程学报，2003，23（1）：74-79.CHE Renfei，LI Renjun.A new three-phase power flow method for weakly meshed distribution systems［J］.Proceedings of the CSEE，2003，23（1）：74-79.

［17］刘一兵，吴文传，张伯明，等.基于混合整数二阶锥规划的三相有源配电网无功优化［J］.电力系统自动化，2014，38（15）：58-64.LIU Yibing，WU Wenchuan，ZHANG Boming，et al.Reactive power optimization for three-phase distribution networks with distributed generators based om mixed integer second-order cone programming［J］.Automation of Electric Power Systems，2014，38（15）：58-64.