基于傅里叶级数建模的双有源桥DC-DC变换器电流有效值分析
2017-05-22马志鹏沙广林
程 红 ,马志鹏 ,王 聪 ,沙广林
(中国矿业大学(北京)机电与信息工程学院 电气工程系,北京 100083)
0 引言
为更好地接纳分布式能源和直流负荷,交、直流混合配电网将成为智能配电系统的重要发展方向[1]。其中双有源桥DAB(Dual-Active-Bridge)DC-DC变换器作为电力电子变压器、固态直流变压器等智能配电设备的核心组成部分,对提升智能配电系统的电能质量、可靠性与运行效率起到了至关重要的作用[2-8]。
在智能配电系统的配电过程中,当微网与主干电网连接,或在多直流微网之间实现不同电压等级的互联时,均需要智能配电接口设备具有按照调度要求双向传输所需功率的功能。当直流微网直接接直流负载时还需要接口设备具有能够给出稳定的直流侧电压或电流的功能。这些功能都需要通过灵活合理地控制DAB变换器来实现。因此怎样利用DAB变换器自身合理的控制实现能量双向流动,充分利用自身的灵活性对资源进行优化配置,以及实现配电设备的高效率和高功率密度,成为近年来专家学者研究的热点内容之一[9]。
目前,DAB变换器在传统单移相控制SPS(Single Phase Shift)方式下能实现能量的双向传递,且控制简单,但传统单移相控制方式只有一个控制自由度,降低了变换器控制的灵活性。当变换器工作在升、降压状态(即直流侧电压不匹配)时,中间交流环节电感电流有效值、变换器的无功功率会随着电压不匹配程度变大而增加,同时增加了变换器的通态损耗,降低了变换器的效率。
为了改善变换器的工作状态,文献[10-11]提出一种只在超前桥引入内移相角的双重移相控制DPS(Dual Phase Shift)方式;文献[12-13]提出一种在超前桥和滞后桥同时引入相等内移相角的双重移相控制方式,在提高变换器控制自由度和控制灵活性的同时,优化变换器的无功功率。但这些文献只讨论了相应控制方式下超前桥无功功率(环流功率)的优化控制,并没有考虑优化超前桥功率特性时对变换器滞后桥功率特性的影响。文献[14-15]考虑直流侧电压不匹配情况,提出在超前桥引入内移相角的双重移相控制方式,优化电感电流应力,但没有对电压不匹配的具体情况(升压、降压)进行讨论,也没有考虑变换器工作在电压不匹配状态时在超前桥或者滞后桥引入内移相角这种2种不同的双重移相控制方式对变换器性能的影响。
文献[10-15]采用瞬时功率积分的方式进行建模,但是这种建模方法计算量大、过程复杂,且对于各种移相控制方式的建模不能进行统一分析。文献[16-18]提出了傅里叶级数求和的建模方法,通过建立移相控制下DAB变换器输入、输出侧方波电压的傅里叶表达形式,建立变换器的复功率模型,然而只对变换器的软开关特性进行分析,并没有建立变换器中间交流环节电感电流有效值的数学模型,不能得出电感电流有效值随内移相角的变化情况,也没有从电感电流有效值优化的角度对变换器运行状态进行分析。
针对以上研究不足,本文采用傅里叶级数求和的方法对工作在移相控制下的DAB变换器进行数学建模,并进一步推导出变换器统一的电感电流时域表达式、有效值表达式及复功率表达式。详细分析了传统单移相控制方式下DAB变换器工作在升压、降压、电压平衡状态时,电感电流有效值随传输有功功率的变化特性,并解释了电压不平衡(升、降压状态)时电感电流有效值较大的原因。在此基础上,综合考虑变换器超前桥和滞后桥的功率特性提出以电感电流有效值这一更直接、全面衡量变换器通态损耗的影响因素为优化目标,针对DAB变换器工作在升、降压状态下电感电流过大的问题,提出了在电压较高的一侧引入内移相角的双重移相控制方式,分析变换器在该控制方式下电感电流有效值变化特性,分析表明采用该双重移相控制策略不仅减小了变换器电感电流的有效值,同时增加了变换器调节的灵活性,减小了变换器的通态损耗,进一步提高了变换器的整体效率。
1 DAB移相控制的数学模型
1.1 DAB变换器等效模型
DAB DC-DC变换器电路如图1所示,主要由2个对称H桥(HB1、HB2)和中间高频隔离变压器T、辅助电感LS组成。图中,Uin为输入侧直流电压;Uout为输出侧直流电压;Ci1、Ci2为输入侧电容;Co1、Co2为输出侧电容;RL为辅助漏感等效电阻;iL为漏感电流;Uab和Ucd分别为变压器原边和副边的交流方波电压。
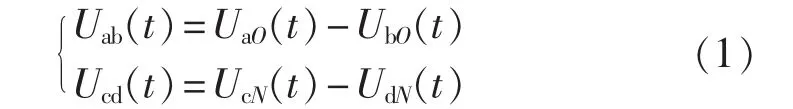
其中,UaO(t)、UbO(t)分别为超前桥 HB1的 a、b 相对于O 点的电压;UcN(t)、UdN(t)分别为滞后桥 HB2的 c、d相对于 N 点的电压;Uab(t)、Ucd(t)分别为超前桥 HB1与滞后桥HB2交流侧正负对称方波电压。

图1 双有源桥DC-DC变换器拓扑Fig.1 Topology of dual-active-bridge DC-DC converter
由傅里叶级数可以将 Uab(t)、Ucd(t)等效成无限次频率倍数关系的正弦电压和的形式,其等效电路模型可表示为图2。
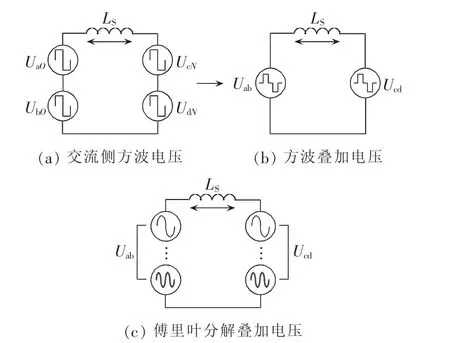
图2 等效电路图Fig.2 Equivalent circuits
移相控制下以能量由超前桥HB1向滞后桥HB2传输为例,以超前桥HB1中桥臂HB11的电压为参考零相位,定义桥臂HB12与桥臂HB11之间的移相角为α1,桥臂HB21与桥臂HB11之间的移相角为α2,桥臂HB22与桥臂HB11之间的移相角为α3。其中α1表示超前桥HB1的内移相角,α2-α1表示超前桥 HB1与滞后桥HB2之间的外移相角,α3-α2表示滞后桥HB2的内移相角,如图3所示。
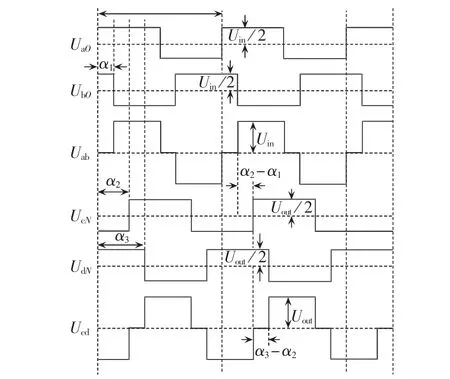
图3 波形叠加原理图Fig.3 Schematic diagram of wave superposition
1.2 傅里叶级数形式数学模型
DAB 变换器电压 UaO(t)、UbO(t)、UcN(t)、UdN(t)表示为傅里叶级数求和的形式,可得其电压时域表达式:
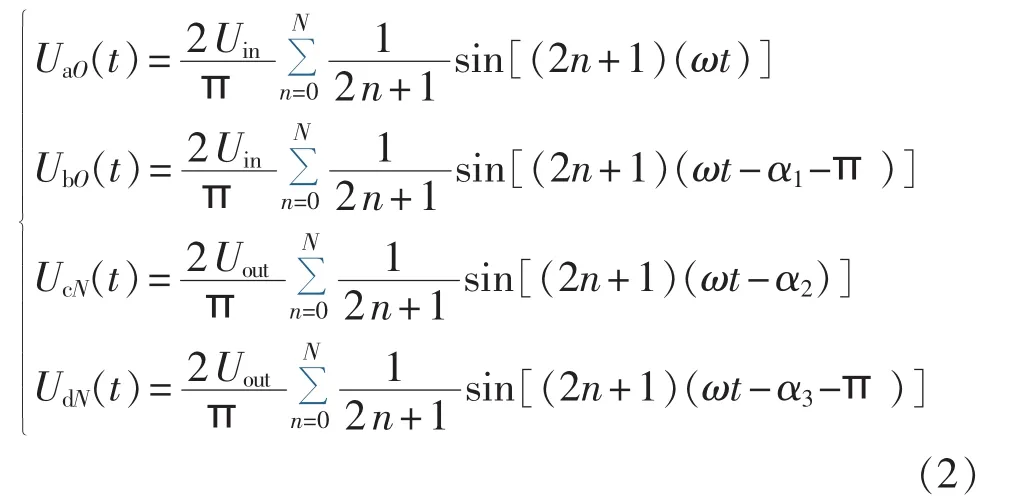
将式(2)代入式(1)可得DAB变换器交流环节Uab(t)、Ucd(t)电压时域表达式:
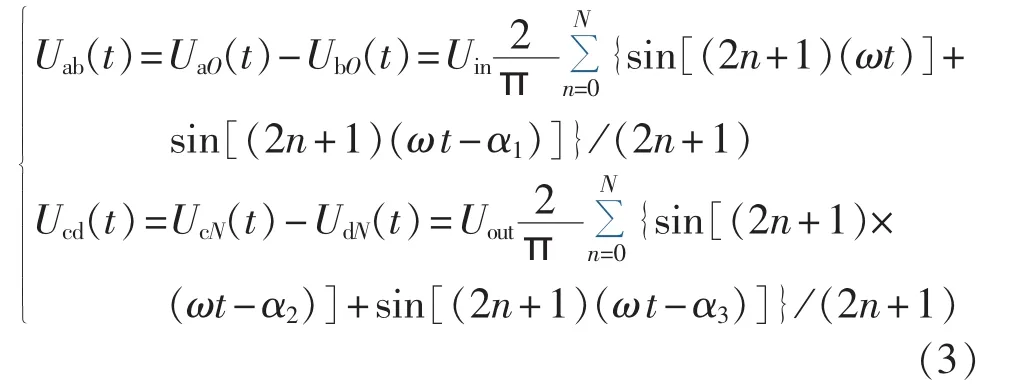
为分析DAB变换器的升压、降压特性,给定变压器的变比为1∶1,可得DAB变换器交流环节电路状态的时域微分方程:
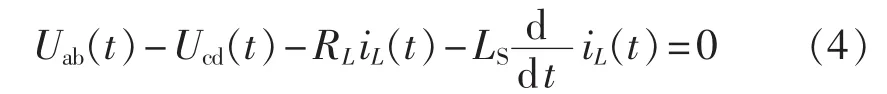
其中,iL(t)为电感电流。忽略高频变压器电感的阻抗(RL=0)时(下同),由式(3)、(4)可得 DAB 变换器电感电流表达式:
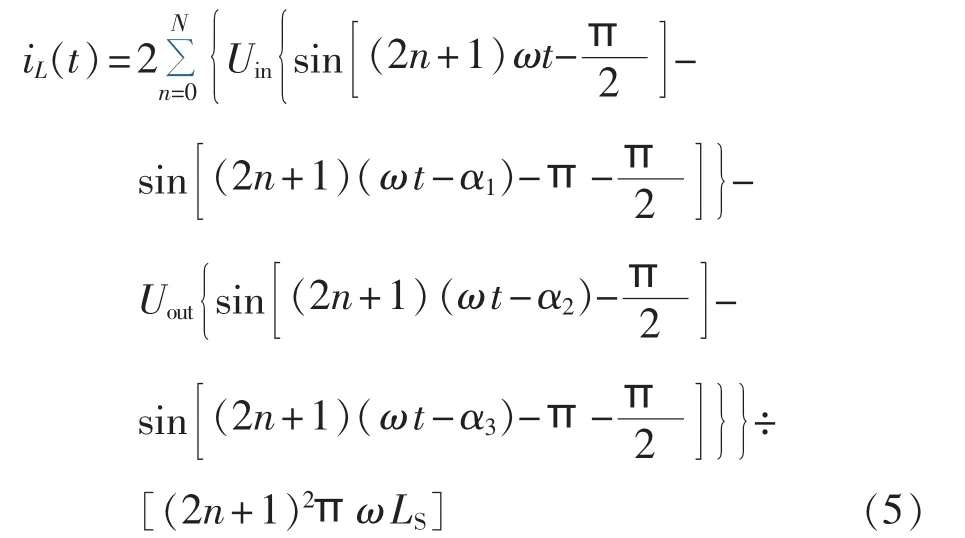
由式(5)得电感电流有效值:
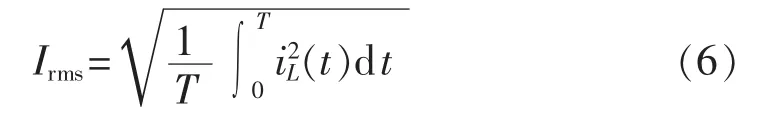
其中,1/T为变换器的开关频率。由式(3)可得交流方波电压傅里叶级数对应的电压相量表达式:

其中,2n+1(n=0,1,2,…)为2n+1 次谐波分量。由式(5)、(7)得电感上的电流相量表达式:
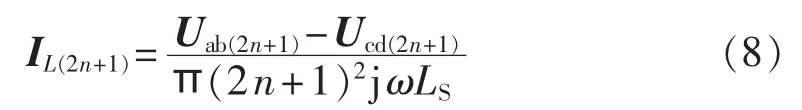
DAB变换器的复功率数学模型如下。
DAB变换器超前桥功率表达式为:


DAB变换器滞后桥功率表达式为:
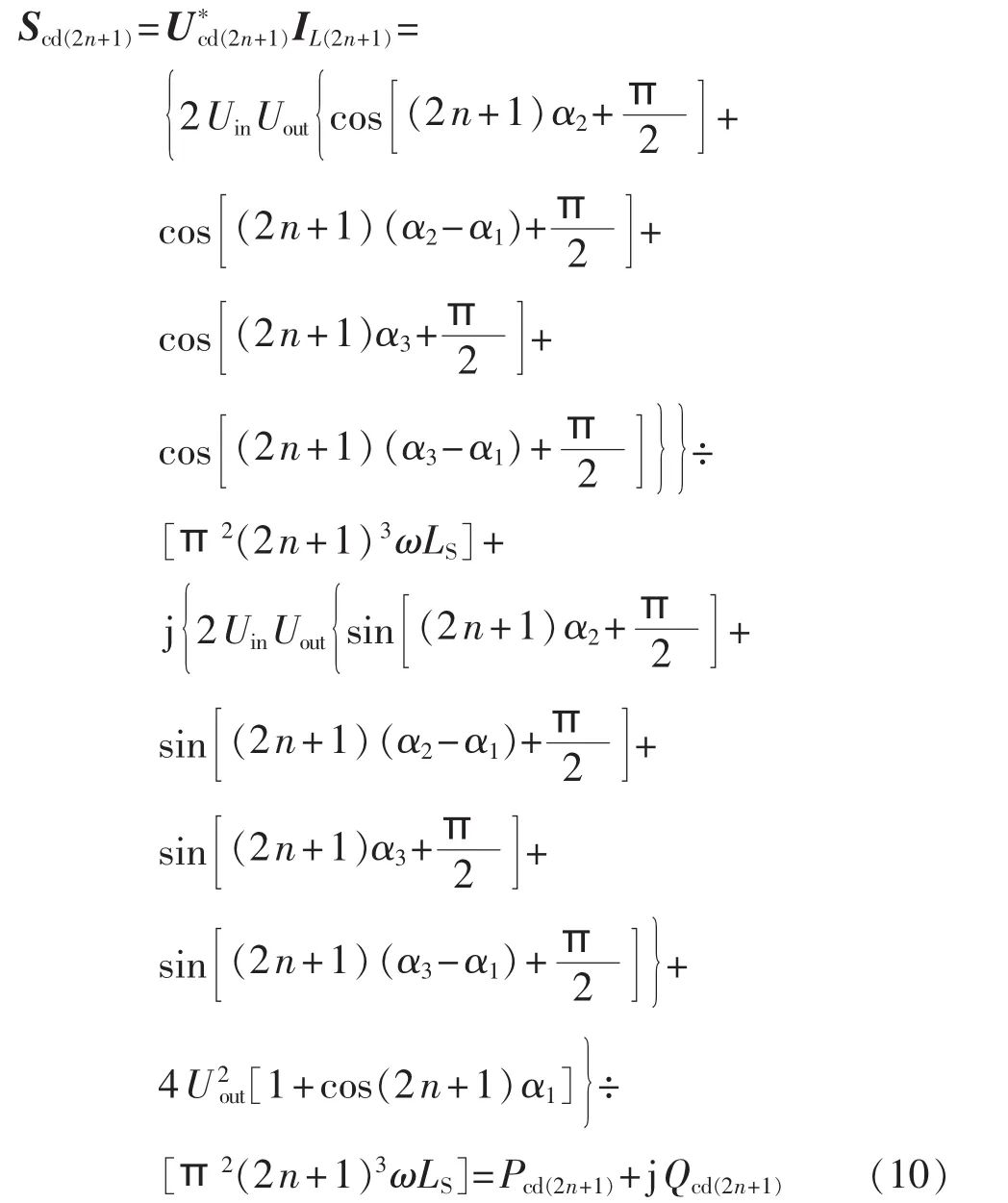
其中,为Uab(2n+1)的共轭复数;的共轭复数;超前桥实部Pab(2n+1)为DAB变换器运行时超前桥输入有功功率,虚部Qab(2n+1)为超前桥无功功率;同理,滞后桥实部 Pcd(2n+1)为输出有功功率,虚部 Qcd(2n+1)为滞后桥无功功率。
2 传统单移相控制电感电流特性
设定Uout=kUin,其中k为DAB变换器升、降压系数,当 α1=0 且 α2=α3时,由式(5)、(9)、(10)可得传统单移相控制下传输功率、电感电流有效值表达式:
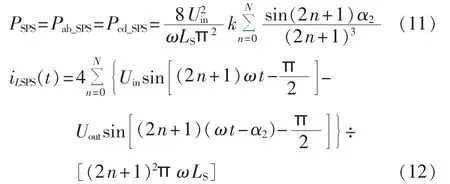
为了分析方便,将传输有功功率、电感电流有效值标幺化,取传统单移相控制下直流侧电压匹配(k=1)时的最大传输有功功率为标幺化功率PN,电感电流有效值最大为标幺化电流IrmsN,则有:
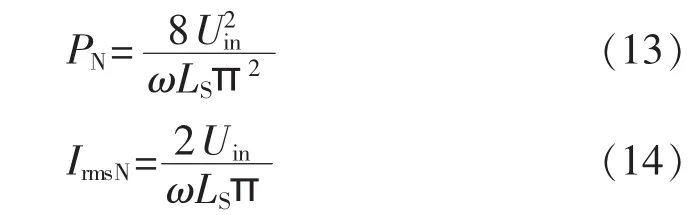
根据式(11)、(13)可以得到传统单移相控制下标幺化传输有功功率,根据式(12)、(14)可得传统单移相控制下标幺化电感电流有效值。
DAB变换器在传统单移相控制下在传输相同的有功功率时,变换器工作在电压平衡(k=1)、升压(k=1.3)、降压(k=0.7)状态下电感电流有效值的关系如图4所示。
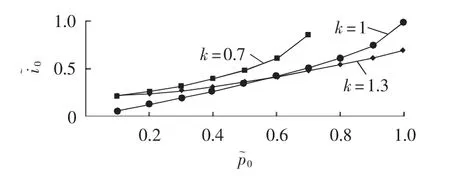
图4 电感电流有效值与传输功率关系图Fig.4 Curve of effective inductor current vs.transferred active power
由图4可以得出,电感电流有效值不仅与变换器传输有功功率大小有关,还与变换器直流侧电压的匹配程度有密切关系,从傅里叶级数分解角度可以得出,变换器直流侧电压匹配的情况直接影响DAB变换器 Uab(t)、Ucd(t)等效成的各不同频率正弦电压幅值的大小,也正是由于各频率尤其是基波电压幅值的不匹配,才造成电感电流有效值发生变化,从而解释了变换器在传统单移相控制下,当直流侧电压不匹配时电感电流有效值较大的原因。
3 双重移相控制漏电感电流特性
传统单移相控制方式只有一个控制自由度,因此不能对变换器 Uab(t)、Ucd(t)等效成的各不同频率正弦电压幅值的大小进行调节,本文引入双重移相控制方式,即在超前桥或滞后桥内引入移相角,通过增加内移相可以提高DAB变换器调节的灵活性,调节变换器 Uab(t)、Ucd(t)等效成的各不同频率正弦电压幅值的大小,匹配变换器直流侧电压,优化电感电流有效值。
3.1 双重移相控制方式分析
双重移相控制方式有2种引入内移相角的方式:超前桥引入内移相角,即α1≠0且α2=α3;滞后桥引入内移相角,即 α1=0 且 α2<α3。由式(5)、(9)、(10)可得不同双重移相控制下传输功率和电感电流表达式。
超前桥引入内移相角时,可得:
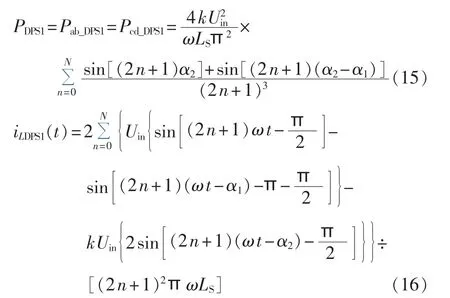
滞后桥引入内移相角时,可得:
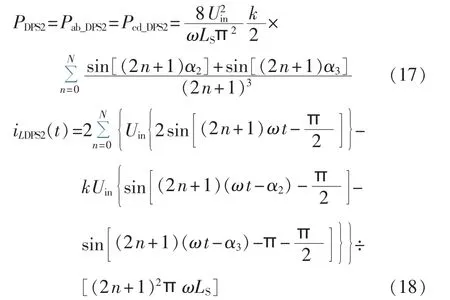
由式(13)、(15)、(17)可得不同双重移相控制方式下标幺化传输有功功率根据式(14)、(16)、(18)可得不同双重移相控制方式下标幺化电感电流有效值。
3.2 漏电感电流有效值分析
变换器直流侧电压匹配具有多种情况,下面以传输有功功率和,以 k=1、k=0.7、k=1.3为例来分析变换器工作在电压匹配、升压、降压状态下传输相同有功功率时,电感电流随引入内移相角的变化情况。
3.2.1 DAB 变换器工作在电压平衡状态
变换器工作在电压平衡状态下传输相同有功功率时,2种不同双重移相控制方式下的电感电流有效值随引入内移相角的变化关系如图5所示。
由图5可知,DAB变换器工作在电压平衡状态时,在超前桥或者滞后桥引入内移相角时电感电流的变化曲线重合,不难理解DAB变换器电压平衡时电气特性是对称的。并且无论在超前桥还是滞后桥引入内移相角,都会使变换器电感电流有效值增加。
3.2.2 DAB 变换器工作在降压状态
变换器工作在降压状态下传输相同有功功率时,2种不同双重移相控制方式下的电感电流有效值随引入内移相角的变化关系如图6所示。

图5 电压平衡时内移相角与电感电流关系Fig.5 Curve of inductor current vs.internal phase-shift angle in balanced voltage condition
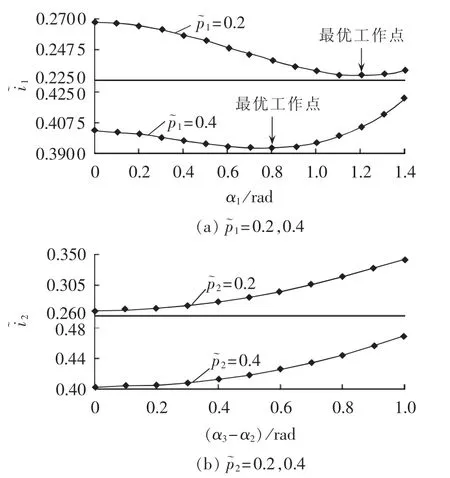
图6 降压状态下内移相角与电感电流关系Fig.6 Curve of inductor current vs.internal phase-shift angle in bucking voltage condition
由图6可知,变换器工作在降压状态时,在超前桥引入内移相角可以有效改变电感电流的有效值,并且随着内移相角的增加,电感电流有效值先减小而后增加(见图6(a)),然而在滞后桥引入内移相角会使电感电流的有效值进一步增加(见图6(b))。
3.2.3 DAB 变换器工作在升压状态
变换器工作在升压状态下传输相同有功功率时,2种不同双重移相控制方式下的电感电流有效值随引入内移相角的变化关系如图7所示。
由图7可知,变换器工作在升压状态时,引入内移相角可以改变电感电流的有效值,在超前桥引入内移相角会使电感电流的有效值逐渐变大(见图7(a)),随着滞后桥引入的内移相角的增加,电感电流有效值先减小而后增加(见图7(b))。
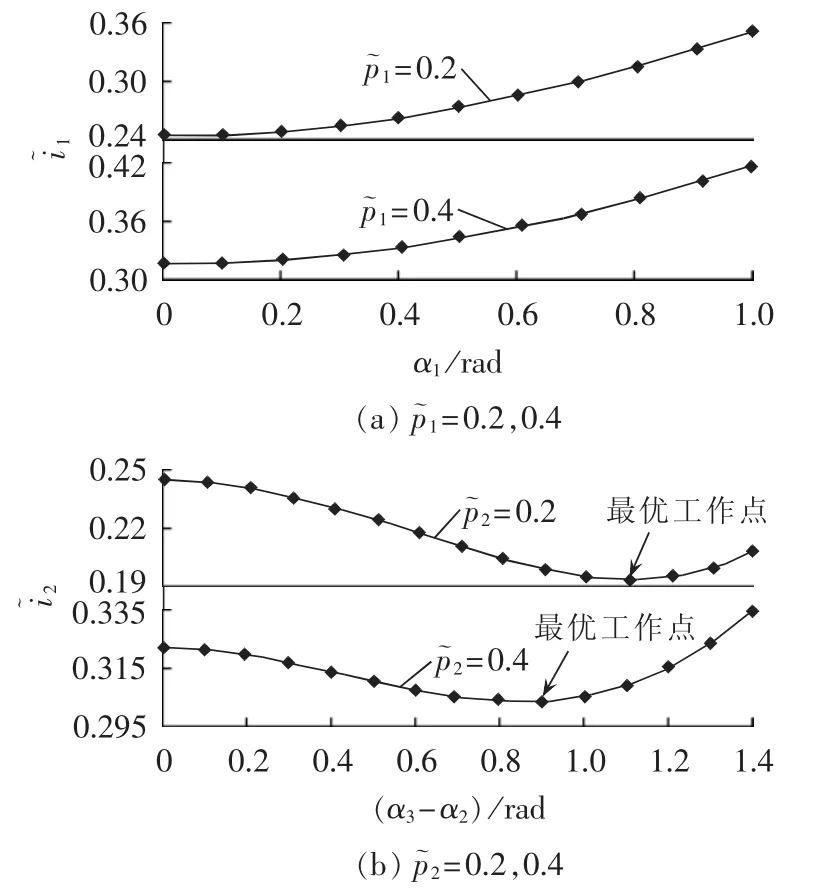
图7 升压状态下内移相角与电感电流关系Fig.7 Curve of inductor current vs.internal phase-shift angle in boosting voltage condition
3.3 优化电感电流有效值
DAB变换器工作在直流侧电压匹配、升压、降压状态下,分析传输相同有功功率时电感电流随不同双重移相控制方式的变化情况,可以得出:
a.当变换器工作在电压匹配状态时,不能通过在超前桥或者滞后桥引入内移角的双重移相控制方式优化电感电流的有效值,以减小变换器的通态损耗,因此变换器直流侧电压匹配时采用传统单移相控制策略具有更好的功率特性;
b.当变换器工作在降压状态时,在超前桥引入内移相角可以有效地减小电感电流的有效值,并且根据电感电流有效值的变化趋势得到最优的超前桥内移相角度,使变换器电感电流有效值最小(见图6(a));
c.当变换器工作在升压状态时,在滞后桥引入内移相角可以有效地减小电感电流的有效值,并且根据电感电流有效值的变化趋势得到最优的滞后桥内移相角度,使变换器电感电流有效值最小(见图7(b))。
4 实验分析
以TMS320F28335为控制器搭建DAB变换器实验平台,图8为实验过程中所采用的控制结构框图,通过α2调节外移相角使输出电压稳定到给定值,通过α1或α3调节内移相角匹配DAB变换器中间交流环节电压。图中,Uref为DAB变换器直流输出侧电压给定;f为移相角控制函数。
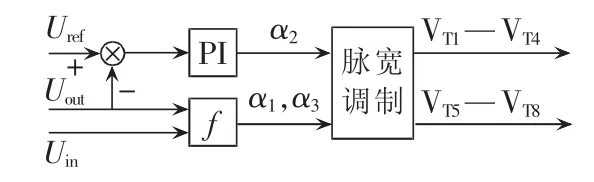
图8 控制框图Fig.8 Control block diagram
主要电路参数如下:Uin=200V,Uout=140~260V,LS=50 μH,C=2200 μF,fS=20 kHz,变压器 T 变比为1∶1。
当输入电压为200 V、输出电压为200 V、变换器工作在电压平衡状态时,传输功率为1.5 kW,电感电流有效值随内移相角的变化情况如图9(a)所示;当输入电压为200 V、输出电压为140 V、变换器工作在降压状态时,传输功率为1.5 kW,电感电流有效值随内移相角的变化情况如图9(b)所示;当输入电压为200 V、输出电压为260 V、变换器工作在升压状态时,传输功率为1.5 kW,电感电流有效值随内移相角的变化情况如图9(c)所示。
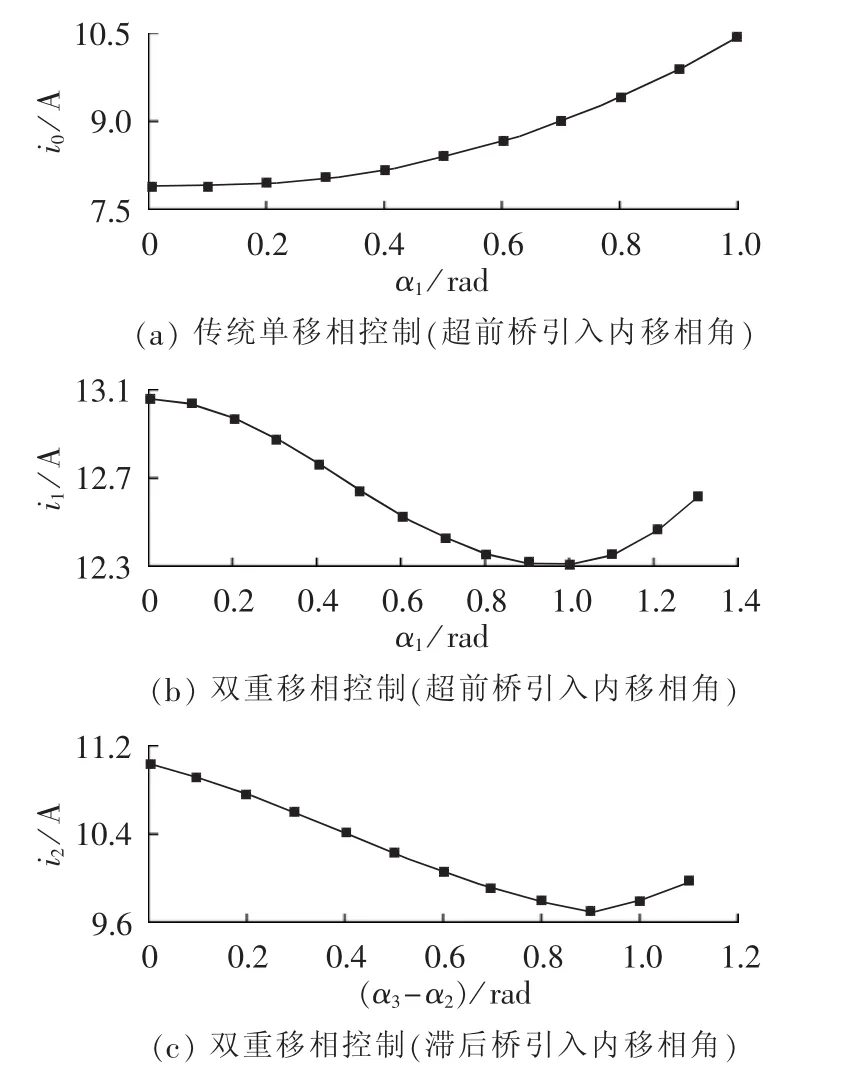
图9 电感电流有效值随内移相角的变化关系Fig.9 Curve of effective inductor current vs.internal phase-shift angle for different voltage conditions
图10为电压平衡、降压、升压状态时,变换器在传统单移相和双重移相控制方式下交流环节电压Uab、Ucd及电感电流iL的波形图。
实验结果显示:当DAB变换器工作在直流侧电压匹配状态时采用传统单移相控制方式,当变换器工作在直流侧电压不匹配状态时采用双重移相控制方式,在电压高的一侧引入适当的内移相角,可以使变换器工作在电感电流有效值最小的状态。
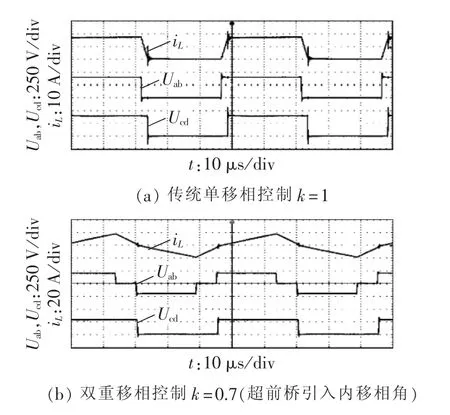
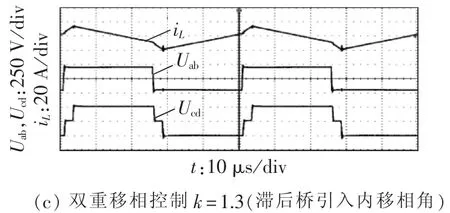
图10 实验波形图Fig.10 Experimental waveforms
5 结论
本文基于傅里叶级数求和的方法建立移相控制下DAB变换器的数学模型,清晰、准确地描述了DAB变换器在移相控制方式下传输相同有功功率时,电感电流有效值随引入内移相角的变化情况,通过分析叠加的各不同频率正弦波幅值的变化,解释了传统单移相控制下,DAB变换器工作在升、降压状态时电感电流有效值变大的原因,以此为基础提出了优化DAB变换器工作在升、降压状态的双重移相控制方式,即在高压侧引入内移相角的双重移相控制方式,优化减小电感电流的有效值,并通过实验验证了该控制方式的有效性和优越性。
参考文献:
[1]周稳,戴瑜兴,毕大强,等.交直流混合微电网协同控制策略[J].电力自动化设备,2015,35(10):51-57.ZHOU Wen,DAI Yuxing,BI Daqiang,et al.Coordinative control strategy for hybrid AC-DC microgrid[J].Electric Power Automation Equipment,2015,35(10):51-57.
[2]HUANG A Q,CROW M L,HEYDT G T,et al.The Future Renewable Electric Energy Delivery and Management(FREEDM)system:the energy internet[J].Proceedings of the IEEE,2011,99(1):133-148.
[3]夏向阳,孔祥霁,帅智康,等.基于磁集成结构DC-DC变换器的超级电容储能系统[J].电力自动化设备,2014,34(11):95-99.XIA Xiangyang,KONG Xiangji,SHUAIZhikang,etal.Supercapacitor energy storage system based on DC-DC converter with integrated magnetic structure[J].Electric Power Automation Equipment,2014,34(11):95-99.
[4]毕大强,赵润富,葛宝明,等.直流微电网能量控制策略的研究[J].电源学报,2014(1):1-7.BI Daqiang,ZHAO Runfu,GE Baoming,et al.A novel energy control strategy for DC microgrid photovoltaic power generation[J].Journal of Power Supply,2014(1):1-7.
[5]侯聂,宋文胜,王顺亮.全桥隔离DC/DC变换器相移控制归一化及其最小回流功率控制[J].中国电机工程学报,2016,36(2):499-506.HOU Nie,SONG Wensheng,WANG Shunliang.Normalization of phase shift control and minimum reflux power control of fullbridge isolated DC /DC converters[J].Proceedings of the CSEE,2016,36(2):499-506.
[6]WU K,SILVA C W,DUNFORD W G.Stabilityanalysisof isolated bidirectional dual active full-bridge DC-DC converter with triple phase-shift control[J].IEEE Transactions on Power Electronics,2012,27(4):2007-2017.
[7]吴雄,王秀丽,刘世民,等.微电网能量管理系统研究综述[J].电力自动化设备,2014,34(10):7-14.WU Xiong,WANG Xiuli,LIU Shimin,et al.Summary of research on microgrid energy management system[J].Electric Power Automation Equipment,2014,34(10):7-14.
[8]TAO H,DUARTE J L,HENDRIX M A M.High-power threeport three-phase bidirectional DC-DC converter[C]∥2007 IEEE Industry Applications Annual Meeting.New Orleans,LA,USA:IEEE,2007:2022-2029.
[9]李霞林,郭力,王成山,等.直流微电网关键技术研究综述[J].中国电机工程学报,2016,36(1):2-17.LI Xialin,GUO Li,WANG Chengshan,et al.Key technologies of DC microgrids:an overview[J].Proceedings of the CSEE,2016,36(1):2-17.
[10]赵彪,于庆广,孙伟欣.双重移相控制的双向全桥DC-DC变换器及其功率回流特性分析[J].中国电机工程学报,2012,32(12):43-50.ZHAO Biao,YU Qingguang,SUN Weixin.Bidirectionalfullbridge DC-DC converters with dual phase-shifting control and its backflow power characteristic analysis[J].Proceedings of the CSEE,2012,32(12):43-50.
[11]程红,高巧梅,朱锦标,等.基于双重移相控制的双向全桥DCDC变换器动态建模与最小回流功率控制[J].电工技术学报,2014,29(3):245-253.CHENG Hong,GAO Qiaomei,ZHU Jinbiao,etal.Dynamic modeling and minimum backflow power controlling of the bidirectional full-bridge DC-DC converters based on dual-phaseshifting control[J].Transactions of China Electrotechnical Society,2014,29(3):245-253.
[12]OGGIER G G,GARCIA G O,OLIVA A R.Switching control strategy to minimize dual active bridge converter losses[J].IEEE Transactions on Power Electronics,2009,24(7):1826-1838.
[13]BAI H,MI C.Eliminate reactive power and increase system efficiency ofisolated bidirectionaldual-active-bridge DC-DC converters using novel dual-phase-shift control[J].IEEE Transactions on Power Electronics,2008,23(6):2905-2914.
[14]王玉斌,王杉杉,封波,等.基于双重移相控制的双有源DC-DC变换器 的 最优电流 控 制[J].电工技术学报,2015,30(14):488-496.WANG Yubin,WANG Shanshan,FENG Bo,etal.Optimal current control strategy of dual-active-bridge DC-DC converter based on dual-phase-shift control[J].Transactions of China Electrotechnical Society,2015,30(14):488-496.
[15]ZHAO B,SONG Q,LIU W,et al.Current-stress-optimized switching strategy of isolated bidirectional DC-DC converter with dualphase-shift control[J].IEEE Transactions on Industrial Electronics,2013,60(10):4458-4467.
[16]SEGARAN D,MCGRATH B P,HOLMES D G.Adaptive dynamic control of a bi-directional DC-DC converter[C]∥2010 IEEE Energy Conversion Congress and Exposition.Atlanta,GA,USA:IEEE,2010:1442-1449.
[17]RIEDEL J,HOLMES D G,TEIXEIRA C,et al.Harmonic-based determination of soft switching boundaries for 3-level modulated single-phase dual active bridge converters[C]∥2015 IEEE Energy Conversion Congress and Exposition(ECCE).Montreal,QC,Canada:IEEE,2015:1505-1512.
[18]WANG Cong,SHA Guanglin,CHENG Hong,et al.Unified phasor analytical method for dual-active-bridge DC/DC converter under phase-shift control[C]∥2016 IEEE 8th International Power Electronics and Motion Control Conference(IPEMC-ECCE Asia).Hefei,China:IEEE,2016:348-355.
