基于高频高压电除尘用LCC谐振电源特性的网侧整流方式比较

刘和平 ，罗 异 ，刘 庆 ，邓 力 ，周 奇

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400030；2.重庆赛力盟电机有限责任公司，重庆 401329）

0 引言

电除尘器是高效率除尘设备，其所需直流高电压由大功率变换器提供，这些变换器典型的功率范围为10～120 kW，输出直流高电压的调节范围为30～100 kV［1］。为降低功耗，常采用高频谐振变换器作为供电电源［2-3］。文献［4-5］证明串联谐振变换器因在较宽电压范围内具有平均充电电流恒定且抗负载短路能力强的优点而被广泛用于电除尘电源系统，并分析了其调压特性，但高压高频变压器寄生参数的影响使其实际工作特性与理想情况存在差别［6］。LCC串并联谐振变换器能充分利用变压器寄生参数，是大功率高频高压电除尘电源的理想选择，为实现逆变桥开关零电流开通、零电流零电压关断的全时软开关效果，根据高压整流器输出电流的不同可使其工作于双脉冲模式或单脉冲模式［7-8］。在LCC串并联谐振变换器工作于这2种模式下仅调节逆变桥频率来调节输出电压的过程中，谐振电感电流持续工作在断续模式，断续程度变化较大时谐振电流峰值会出现极大值，频率调节区间过大时变换器工作模式将会发生改变，从而使特性改变，当输出为单脉冲模式时还会使开关关断时间不易确定［9］。但目前电除尘电源系统前级普遍采用三相不可控二极管整流器输出直流母线电压为后级供电，由于直流母线电压不可控，使得当后级工作模式变化引起其值变化时会引起电网电流较大的畸变［10］，使网侧功率因数较低，并且仅能通过调节后级高频变换器频率来调节高压侧输出电压，增大输出功率。同时，由于直流母线电压最大值仅为电网相电压有效值的2.45倍，为使高压侧电压达到电晕电压等级，往往需要高频升压变压器变比很大，这给设计带来困难，也使得寄生参数值较大。目前很少有文献深入分析LCC串并联谐振变换器的调压特性，同时，虽然高功率因数整流器在高压大容量场合应用较多［11］，但有关研究其在高压大功率电除尘电源系统中应用的文献却很少。

本文深入分析了电除尘电源系统后级LCC串并联谐振变换器双脉冲工作模式，分时间段建立了变换器数学模型并进行详细的特性分析。基于后级工作特性对比不同高功率因数整流方式应用于电除尘电源系统前级时整机特性的不同，分别设计具有代表性的无源及有源功率因数校正功能的近正弦输入电流整流器（RNSIC）及脉宽调制（PWM）整流器作为前级整流器，根据后级额定功率分别设计整流器参数，在电力电子Saber仿真软件中进行大量的分析工作，对比了2个系统在这2种整流设备提供直流母线电压条件下后级分别采用调频调压及调节直流母线电压调压方式下的工作特性，为高功率因数整流器在高频高压大功率电除尘电源系统中的应用提供了参考。

1 LCC谐振变换器双脉冲模式分析

高频高压电除尘电源系统拓扑如图1所示，前级为三相整流器，后级为LCC串并联谐振变换器。根据一个谐振电流周期内后级高压侧整流桥输出电流io的不同可以分为双脉冲及单脉冲2种工作模式，其区别在于当 VTs1、VTs4（VTs2、VTs3）开通时并联电容 Cp上的电压值是否已被箝位到Uo/n或-Uo/n。谐振电感电流工作于这2种模式时可以实现逆变桥开关零电流开通、零电流零电压关断的全时软开关效果。对于单脉冲模式，在每个谐振电流周期开始时存在为并联电容继续充电的时间段，使得逆变桥开关关断时间不确定，不利于逆变器控制。

本文重点分析双脉冲模式下变换器特性，为便于建立数学模型，定义如下变量：电容比k=Cp/Cs；特征阻抗；谐振角频率。并假设：变换器各元件均为理想器件；直流母线电压Ud和输出电压Uo恒定；滤波电容Co折算到变压器初级的值远大于串、并联电容值（Cs、Cp）。双脉冲模式下主要波形如图2所示。为实现软开关的目的，要求一个开关周期内开关管驱动时间Ton小于一个谐振电流周期TLs且TLs要小于开关周期的一半。以t1为一个谐振电流周期开始时刻为例，谐振电流为正的时间段［t1，t2）为谐振角频率一定的半个正弦波周期，在谐振电流为负的时间段［t2，t3）内关断开关可实现零电流零电压关断效果，大幅减小关断过程中功率损耗。半个开关周期内谐振变换器各个模态的工作情况如下。

a.模态 1［t1，t2）。开关管 VTs1、VTs4开通，t1时刻谐振电流iLs（t1）=0，并联电容两端电压已被箝位到Uo/n，谐振电感Ls与串联电容Cs参与谐振，电流从零开始按正弦规律增加，变压器初级向次级传递能量，根据初始条件得到时域状态方程为：

图1 电除尘电源系统拓扑图Fig.1 Topology of electrostatic precipitator power supply system

图2 双脉冲模式主要波形图Fig.2 Main waveforms of double-impulse mode

其中，iLs为谐振电流；UCs为串联电容电压值。

b.模态 2［t2，tx）。在 t2时刻，谐振电流正方向到零，UCs达到峰值，之后谐振电流反向，通过反并联二极管VDs1、VDs4续流，UCs及UCp开始减小，高压侧整流二极管截止，变压器初级无能量传递到次级，Ls、Cp和Cs三元件参与谐振。在该阶段撤去开关管驱动信号则能实现开关管的零电流零电压关断。根据式（1）可得 UCs（t2），该阶段其他初始条件为iLs（t2）=0，UCp（t2）=Uo/n，由此可解得时域状态方程为：

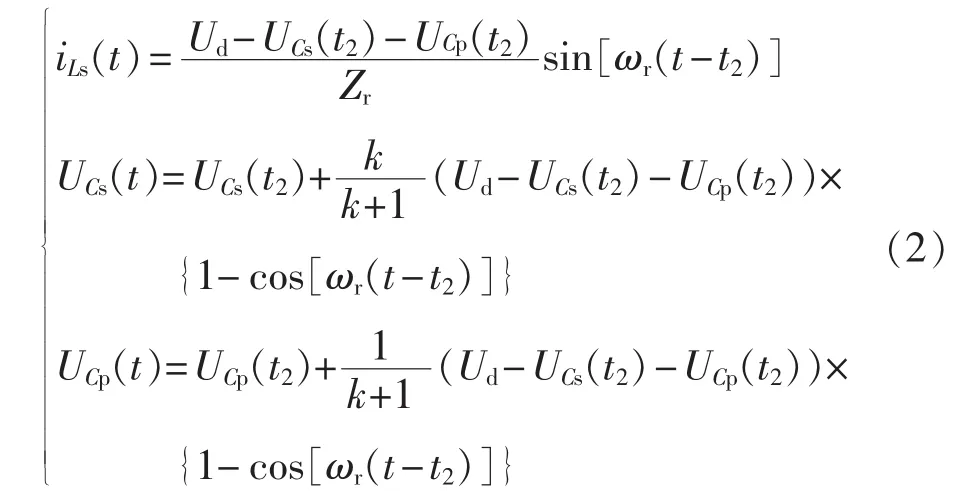
在tx时刻，并联电容电压被谐振电流反向箝位到 -Uo/n，由式（2）可以解得：

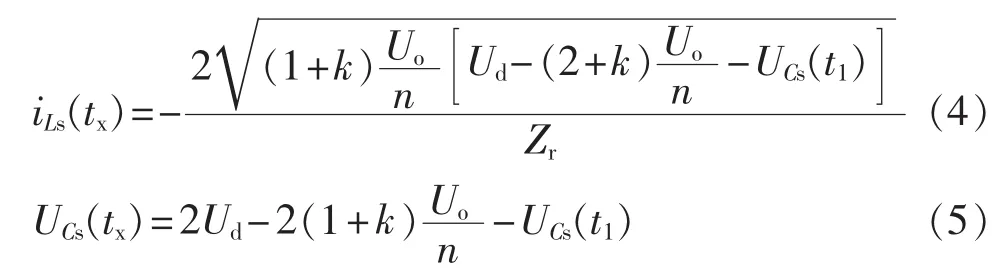
c.模态 3［tx，t3）。该时间段内并联电容 Cp两端电压一直被箝位在-Uo/n，Ls与Cs参与谐振。变压器初级再次向次级传递能量，谐振电流为负，谐振网络储能回馈给输入电源。在该阶段撤去开关管驱动信号也能实现开关管的零电流零电压关断。式（4）、（5）为该阶段初始条件，由此可得时域状态方程为：

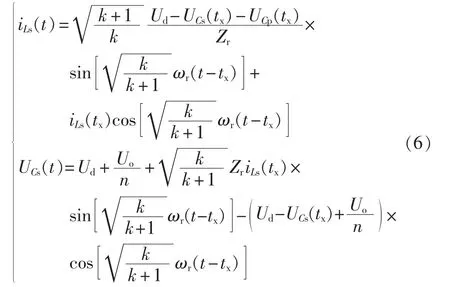
在t3时刻谐振电流再次到零，并联电容Cp两端电压UCp保持-Uo/n不变，UCs达到新的稳定值，由电路工作波形的对称性可知 UCs（t3）=-UCs（t1）、iLs（t3）=-iLs（t1），根据式（6）可得：

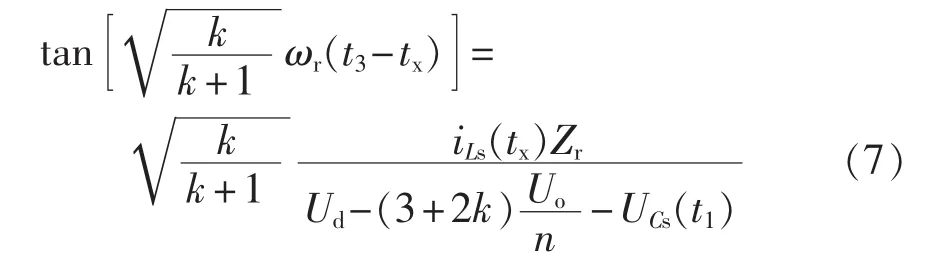
d.模态 4［t3，t4）。该模态谐振电路不工作，UCp与UCs保持不变。该时间段结束后谐振电路开始另一半开关周期的工作。调节该时间段长短可以调节输出电压。特别地，该时间段持续时间为零时为临界电流模式。

双脉冲模式下要求tx变化范围为t2＜tx＜t3。

由式（1）、（2）、（5）及 tx变化范围可解得双脉冲模式下的输出电压限制条件为：

理想情况下变换器输入、输出功率满足：

为表示输入、输出电压关系，定义电压传输系数：

结合各时间段UCp与UCs变化量与谐振电流关系、功率平衡关系并将式（1）、（10）代入，以输入电压Ud作为电压基准值，得到串联电容各时刻归一化电压的表达式为：

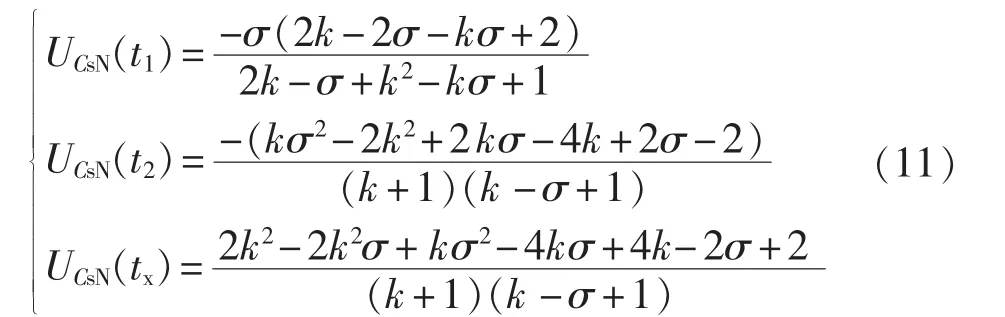
将式（4）、（11）分别代入式（3）、（7）得到一个开关周期内总的谐振电流工作时间为：

当模态4持续时间为零时的逆变器开关频率即为LCC串并联谐振变换器临界频率fr，且fr=1/（2TLs）。以谐振角频率 ωr对应的频率 fωr=ωr/（2π）为频率基准值得到归一化临界频率表达式为：

2 调压特性分析

由式（14）绘出归一化临界频率frN与电压传输系数σ关系曲线如图3所示，可见在电路参数确定时临界频率仅与电压传输系数相关，根据所需电压传输系数即可确定其所对应的临界频率。为使LCC串并联谐振电路工作在双脉冲模式，σ最大值不能超过1，此时，UCp在一个谐振电流周期结束时恰好被箝位到 Uo/n 或 -Uo/n。

图3 归一化临界频率与电压传输系数关系曲线Fig.3 Curves of normalized critical frequency vs.voltage transmission coefficient

定义等效负载系数 Q=Ro/（n2Zr），并令逆变器开关频率fs=xfr，其中x为频率系数，表示断续程度，其变化范围为0到1。由对称性，可建立半个开关周期内能量平衡方程为：

将谐振电流表达式及式（11）、（12）代入式（15）可得到x与Q、σ、k之间数学关系，以k=0.2为例绘出等效负载系数与电压传输系数关系曲线如图4所示。对于相同等效负载系数，频率系数越接近1时所对应的电压传输系数越大，说明临界模式下电压传输比最大，将频率固定在临界频率并调节母线电压时，可得最大斜率的线性调压曲线。将x与Q、σ、k之间的数学关系及式（14）代入逆变器开关频率表达式，得到以fωr为基准值的归一化频率表达式为：

图4 Q与σ关系曲线Fig.4 Curves of Q vs.σ

以Q=0.8为例根据式（16）绘出fsN与k、σ关系曲面如图5所示，由此可得不同k值对应的fsN与σ关系曲线，当fsN接近双脉冲模式极限值时σ变化较平缓，说明LCC串并联谐振变换器采用调频调压方式时调压曲线斜率随频率的增大而逐渐减小，接近临界模式时调压特性较差。

图5 fsN与σ、k的关系曲面Fig.5 Relation surface of fsNvs.σ and k

以 Ud/Zr为谐振电流基准值，由式（1）可得归一化谐振电流峰值为：

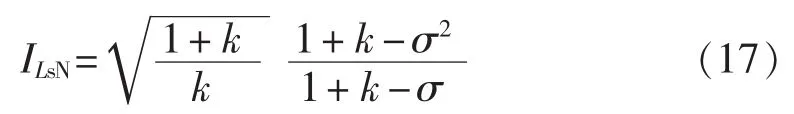
根据式（17）绘出谐振电流峰值曲线如图6所示，可以看出，随着电压传输系数逐渐增大，谐振电流峰值会先增大后减小，在调节高压侧电压过程中会出现极大值，大幅增加了开关管的电流应力。

图6 ILsN与σ关系曲线Fig.6 Curves of ILsNvs.σ

3 电除尘电源系统网侧整流器选择

为提高高压电除尘电源系统网侧电能质量，本文分别采用近正弦输入电流整流器及PWM整流器作为系统网侧变流器，并比较所对应直流母线电压不可控和可控2种情况下整机工作特性。2种整流器拓扑分别如图1前级和图7所示。近正弦输入电流整流器通过网侧电感和二极管并联电容改变电路工作状态，提高网侧功率因数，是采用无源技术抑制谐波方法中具有代表性的一种［12-14］。PWM整流器因具有网侧电流谐波含量小、功率因数高及动态响应快等优点而被广泛用作电力电子设备与电网接口［15-16］。

图7 近正弦输入电流整流器拓扑Fig.7 Topology of nearly-sinusoidal input-current rectifier

4 实例仿真分析及验证

4.1 参数设计

以输出功率106kW、输出电压64kV为2个系统的额定输出指标，取额定输出时母线电压为800 V，并由图3—5设计LCC谐振变换器参数如下：谐振电感 Ls＝15 μH， 串联电容 Cs＝4 μF， 并联电容 Cp＝1.6 μF，变压器变比 1∶n＝1∶140，临界频率 fr＝12.36 kHz，额定母线电压Ud＝800 V。由所设计参数可得σ=0.8，小于双脉冲模式极限值1，可保证变换器工作于该模式。根据后级额定功率及额定母线电压值分别设计前级整流器参数如下：近正弦输入电流整流器，网侧滤波电感 La＝Lb＝Lc＝5 mH， 滤波电容 Cd＝1470 μF，二极管并联电容 C1＝C2＝…＝C6＝ 365.5 μF，最大输出功率 Pomax＝110 kW；PWM 整流器，输入电感 La＝Lb＝Lc＝5 mH，调制频率 fPWM=10 kHz，滤波电容 Cd＝6000 μF，最大输出功率Pomax＝110kW。网侧额定输入为线电压380 V、频率50 Hz的三相交流电，PWM整流器网侧电阻取0.01 Ω。由所设计系统前级整流器及后级谐振变换器参数分别在电力电子Saber仿真平台中搭建2个系统的整机仿真模型。

对于前级采用近正弦输入电流整流器的系统，Ud不可控，只能调节后级开关频率fs来调节Uo，在额定电压以下调节过程中变换器持续工作于断续模式，图8（a）为fs=10 kHz时的谐振电流波形，后级为断续工作模式，测得此时母线电压为858V，已偏离其额定值，谐振电流峰值为577A，其理论计算值为575A。对前级采用PWM整流器的系统，将后级频率保持在临界频率fr，根据Ud所需调节范围确定电网侧相电压，并通过整定控制参数在此范围内调节Ud［17-20］，该过程中后级电源持续工作于临界模式，图8（b）为Ud=800 V时的谐振电流波形，后级为临界模式，测得谐振电流峰值为524 A，其理论计算值为523 A。由谐振电流波形可验证LCC谐振变换器参数设计的正确性。

图8 2种模式下iLs波形Fig.8 Waveforms of iLsin two modes

在输出额定功率时2个系统电网侧波形如图9所示。图9（a）为近正弦输入电流整流器网侧a相电压、电流波形，测得电流总谐波畸变率（THD）为0.014，根据此时电压、电流波形相位差得到位移因数，进而计算得到功率因数为0.999。图9（b）为PWM整流器网侧a相电压、电流波形，测得电流THD为0.011，计算得到功率因数为0.999。可见，在后级工作于额定功率时2个系统网侧功率因数均较高，验证了整流器参数设计的正确性。

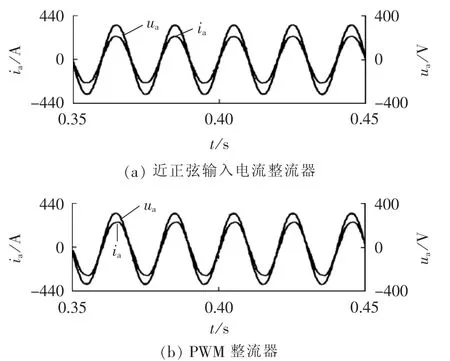
图9 2种整流器电网侧波形Fig.9 Grid-side waveforms of two rectifier types

4.2 工作特性对比

由所测数据绘出2个电除尘电源系统调压特性对比曲线如图10所示，其中近正弦输入电流整流器作为网侧整流器的系统仅能通过调节后级频率来调节输出电压，而PWM整流器作为网侧整流器的系统可以使后级频率固定而采用调节直流母线电压的方式来调节输出电压。

图10 调压特性对比曲线Fig.10 Comparison of voltage regulation performance

由图10（a）可见，在逆变器频率接近临界频率阶段时，调频调压方式下的调压特性变差。而由图10（b）可见，固定逆变器频率为临界频率12.36 kHz，采用调节母线电压调压时，电压传输系数保持0.8不变，因此调压曲线始终保持线性调压特性，结果与理论分析一致。

图11 谐振电流峰值曲线Fig.11 Curves of peak resonant current

2种调压方式下谐振电感电流峰值曲线如图11所示，可见输出电压在额定值以下调节过程中，调频调压方式下所对应的谐振电流峰值较大，最大时达到612 A。若Ud不变，则调频调压方式下谐振电流随输出电压变化趋势应如图6所示，但由于近正弦输入电流整流器直流母线电压不可控，其值随负载功率变化会波动，因此两者存在较小差别。而调节直流母线电压调压方式下所对应的谐振电流保持线性增长，其值较小，在额定输出时达到最大，为524 A，因此在输出电压调节过程中PWM整流器作为前级的电除尘电源系统大幅减小了后级开关电流应力。

2个系统电网侧功率因数与输出功率Po曲线如图12所示，由于近正弦输入电流整流器参数在后级额定功率下设计，所以其功率因数只有在额定功率附近时会接近1，当输出功率较小时，虽然电网电流波形畸变率较小，但位移因数逐渐减小，导致功率因数变小。而PWM整流器对电网电流直接进行控制，在后级负载功率变化过程中电网侧功率因数始终接近1，大幅提高了电除尘电源系统电网侧电能质量。

图12 2个系统电网侧功率因数对比曲线Fig.12 Comparison of grid-side power factor between two systems

5 结论

a.本文分阶段准确建立了电除尘用LCC串并联谐振电源在双脉冲模式下的变换器数学模型，并得到验证，可作为变换器参数设计依据。

b.PWM整流器直流母线电压可控且可调的特点使得将其作为电除尘电源系统前级与电网接口时能将直流母线电压作为电除尘电源系统新的调压变量，与传统调频调压方式相比，调节直流母线电压调压特性更好，输出电压在最大值以下调节过程中谐振电流峰值大幅减小，因此在改善电网电能质量的同时能更好地匹配后级工作特性，说明其在高压电除尘电源系统中具有一定的工程应用价值。

参考文献：

［1］SOEIRO T B，FRIEDLI T，LINNER J，et al.Comparison of electrostatic precipitator power supplies with low effects on the mains［C］∥8th International Conference on Power Electronics-ECCE Asia.Jeju，Korea：IEEE，2011：2382-2389.

［2］刘闯，崔剑峰，刘海洋，等.适合直流配电的有源前端控制器［J］.电力自动化设备，2016，36（7）：104-110.LIU Chuang，CUI Jianfeng，LIU Haiyang，et al.Active front-end controllerforDC distribution［J］.Electric PowerAutomation Equipment，2016，36（7）：104-110.

［3］GRASS N，HARTMANN W，KLÖCKNER M.Application of different types of high-voltage supplies on industrial electrostatic precipitators［J］.IEEE Transactions on Industry Applications，2004，40（6）：1513-1520.

［4］钟和清，徐至新，邹云屏，等.寄生电容对串联谐振电容器充电电源特性的影响［J］.中国电机工程学报，2005，25（10）：40-44.ZHONG Heqing，XU Zhixin，ZOU Yunping，et al.Effects of parasitical capacitors on charging characteristic of series resonant CCPS［J］.Proceedings of the CSEE，2005，25（10）：40-44.

［5］刘军，官威，石健将，等.高压静电除尘用电源调压特性的分析［J］.高电压技术，2009，35（2）：344-349.LIU Jun，GUAN Wei，SHI Jianjiang，et al.Voltage regulation characteristics analysis of power supply for high voltage electrostatic precipitators［J］.High Voltage Engineering，2009，35（2）：344-349.

［6］刘军，郭瑭瑭，常磊，等.高压变压器寄生电容对串联谐振变换器特性的影响［J］.中国电机工程学报，2012，32（15）：16-23.LIU Jun，GUO Tangtang，CHANG Lei，et al.Effects of the parasitic capacitance on characteristics of series parallel converters［J］.Proceedings of the CSEE，2012，32（15）：16-23.

［7］张治国，谢运祥，袁兆梅.LCC谐振变换器工作模式的分析与判别［J］.电力自动化设备，2013，33（5）：50-54.ZHANG Zhiguo，XIE Yunxiang，YUAN Zhaomei.Analysis and identification ofLCC resonantconverteroperating modes［J］.Electric Power Automation Equipment，2013，33（5）：50-54.

［8］YANG Rui，DING Hongfa，XU Yun，et al.An analytical steadystate model of LCC type series-parallel resonant converter with capacitive output filter［J］.IEEE Transactions on Power Electronics，2014，29（1）：328-338.

［9］刘和平，杨依路，刘平，等.电除尘高压电源LCC变换器电流断续模式分析［J］.高电压技术，2014，40（11）：3506-3512.LIU Heping，YANG Yilu，LIU Ping，et al.Analysis of LCC converter in discontinuous mode in electrostatic precipitators high voltage power supply［J］.High Voltage Engineering，2014，40（11）：3506-3512.

［10］SOEIRO T B，MUHLETHALER J，LINNER J，et al.Automated design of a high-power high-frequency LCC resonant converter for electrostatic precipitators［J］.IEEE Transactions on Industrial Electronics，2013，60（11）：4805-4819.

［11］KOLAR J W，FRIEDLI T.The essence of three-phase PFC rectifier systems-partⅠ［J］.IEEE Transactions on Power Electronics，2013，28（1）：176-198.

［12］ALEXA D，SIRBU A，DODREA D M.An analysis of three-phase rectifiers with near-sinusoidal input currents［J］.IEEE Transactions on Industrial Electronics，2004，51（4）：884-891.

［13］陈仲，朱银玉，邱岩，等.近正弦输入电流三相整流器的分析和参数设计［J］.中国电机工程学报，2009，29（36）：29-34.CHEN Zhong，ZHU Yinyu，QIU Yan，et al.Analysis and design of three-phase rectifier with near-sinusoidal input currents［J］.Proceedings of the CSEE，2009，29（36）：29-34.

［14］陈仲，朱银玉，罗颖鹏.基于交流侧LC滤波的近正弦输入电流三相整流器［J］.电工技术学报，2009，24（11）：108-113.CHEN Zhong，ZHU Yinyu，LUO Yingpeng.Three-phase rectifier with near-sinusoidal input currents and LC filters connected on the AC side［J］.Transactions of China Electrotechnical Society，2009，24（11）：108-113.

［15］RODRIGUEZ J R，DIXON J W，ESPINOZA J R，et al.PWM regenerative rectifiers：state of the art［J］.IEEE Transactions on Industrial Electronics，2005，52（1）：5-22.

［16］贾俊川，李卫国.三相电压型PWM整流器控制特性［J］.电力自动化设备，2010，30（4）：63-65.JIA Junchuan，LI Weiguo.Control characteristic of three-phase voltage-source PWM rectifier［J］.Electric Power Automation Equipment，2010，30（4）：63-65.

［17］汪万伟，尹华杰，管霖.双闭环矢量控制的电压型PWM整流器参数整定［J］.电工技术学报，2010，25（2）：67-72.WANG Wanwei，YIN Huajie，GUAN Lin.Parameter setting for double closed-loop vector control of voltage source PWM rectifier［J］.Transactions of China Electrotechnical Society，2010，25（2）：67-72.

［18］王恩德，黄声华.三相电压型PWM整流的新型双闭环控制策略［J］.中国电机工程学报，2012，32（15）：24-30.WANG Ende，HUANG Shenghua.A novel double closed loops control of the three-phase voltage-sourced PWM rectifier［J］.Proceedings of the CSEE，2012，32（15）：24-30.

［19］张建坡，田新成，尹秀艳.模块化多电平换流器直流输电控制策略［J］.电力自动化设备，2015，35（11）：103-108.ZHANG Jianpo，TIAN Xincheng，YIN Xiuyan.Control strategy of MCC-HVDC SVPWM［J］.Electric Power Automation Equipment，2015，35（11）：103-108.

［20］侯世英，张诣.新型数字锁相环在三相电压型SVPWM整流器中的应用［J］.电力自动化设备，2011，31（7）：48-51.HOU Shiying，ZHANG Yi.Application of digital PLL in threephase voltage-source SVPWM rectifier［J］.Electric Power Automation Equipment，2011，31（7）：48-51.