电流品质优化的容错型三相四开关逆变器载波调制算法

朱 翀 ，曾志勇 ，赵荣祥 ，2

（1.浙江大学 电气工程学院，浙江 杭州 310027；2.国家电力电子应用技术工程研究中心，浙江 杭州 310027）

0 引言

电压源型三相六开关逆变器作为一种成熟的拓扑，已广泛应用于电机驱动、有源滤波等工业场合。作为能量转换的核心部件，逆变器的可靠性是保证整个系统安全运行的基础。逆变器一旦发生故障，整个驱动系统将丧失工作能力，在一般工业应用场合会影响正常生产，若在航空航天、军事、医疗等重要行业，则会造成巨大的生命财产损失。然而，由于长时间工作在开关状态，作为逆变器核心部件的功率半导体器件及其驱动控制电路很容易发生故障，其可靠性问题一直没有得到有效解决。据统计，在电力电子设备故障中，约有60%是由于开关器件及其驱动电路故障引起的［1-2］。针对这个问题，国内外的学者提出逆变器容错控制技术，即开关器件故障后通过重新配置逆变器电路拓扑并相应调整控制策略，使逆变器在不间断稳定运行的同时尽可能恢复故障前的性能。为达到这一目标，一种方法是采用开关器件冗余的逆变器结构，在正常运行的开关器件发生故障后立即让冗余器件投入运行［3］，但这将使系统成本增加；另一种方法是使系统在故障后重构为四开关形式，该拓扑中直流母线上下串联2个电容，器件发生故障后将故障相的输出端引至电容中性点，由于只使用了4个开关器件，无需额外增加成本，具有很重要的研究价值［4-7］。

众所周知，逆变器的输出性能与其脉宽调制（PWM）方法密切相关。与六开关逆变器不同，容错四开关逆变器只有4个长度不同的基本开关矢量，且不含零矢量，调制方法更为复杂。已有学者对四开关逆变器的性能与调制方法进行介绍，但都是建立在假设上下两分裂电容的电压值相等的基础上［8-11］。事实上，由于四开关拓扑中一相负载电流直接从电容中性点流出，其势必会对电容中性点电压产生影响，使上下两电容电压波动，从而影响调制性能，输出不平衡的交流电流。文献［12-15］分析了中性点电压不平衡时4个基本电压矢量，并根据参考矢量所处扇区，每个开关周期内选择临近参考矢量的3个基本矢量进行合成。但是，文献中所提方法需要进行繁琐的扇区判断，同时计算有效矢量作用时间时需要三角函数运算，比较复杂，对控制器的实时计算能力提出较高要求。在实际应用中，数字控制器的运算负担重，会产生较大的计算延时，对逆变器的输出性能影响比较大，在开关频率较高的应用场合甚至可能会由于来不及计算下一周期占空比，使输出性能进一步恶化，进而引起驱动系统的二次故障。因此，有必要对四开关逆变器的调制算法进行深入研究，在保证输出性能的同时简化其计算过程，减轻数字控制器的负担。

另一方面，由于四开关逆变器的空间基本矢量中不含零矢量，所以在空间矢量调制时，需要用两方向相反的基本矢量等效合成参考矢量。采用不同的零矢量合成方案，四开关逆变器的PWM输出电压不同，其对输出性能的影响也不同。文献［14］已经指出，相较于正常运行状态下的六开关逆变器，容错型四开关逆变器的输出性能比较差。因此，需要对四开关逆变器的不同调制方式进行分析比较，选择最优方式，使故障后的输出性能尽可能地减小与故障前的差距。文献［16］比较了3种采用不同零矢量合成方式的PWM方案对永磁同步电机转矩的影响，指出采用“劈零矢量”方案的PWM方式可使磁链幅值、角度的动态误差减小，相应地减小转矩脉动，但并未详细推导PWM排布方式与转矩脉动的关系，缺乏理论依据。一般而言，评价调制方式优劣可以用输出电流总谐波畸变率（THD）作为评估标准。但是，分析输出电流的THD需采用离散傅里叶变换（DFT）、跳跃的傅里叶理论（FTJ）等频域分析方法，计算比较复杂，且无法得到统一明确的解析表达式，不便于对影响调制效果的因素进行对比分析。因此，文献［17-19］提出在时域中分析电流纹波有效值的方法替代频域分析方法，并指出电流纹波有效值与电流THD正相关，是一个很好的衡量PWM输出性能的标准。尤其是当负载为电机时，电流纹波有效值直接关系到转矩脉动的大小以及电机发热等指标［20］。在三相四开关逆变器的调制方法分析中，目前并没有文献采用这一分析方法，所以本文选择电流纹波有效值作为评价不同调制方式性能的标准。

本文首先对四开关逆变器的空间矢量调制（SVM）方法进行详细介绍，将空间矢量转换到两相静止坐标系下进行分析，考虑了上下电容电压不平衡时的情况，并在此基础上推导出各基本矢量作用的时间，可以抑制中性点电压波动对输出电流的影响。同时，针对2种不同的零矢量合成方案，以输出电流纹波有效值作为评价标准，分析并计算得到不同调制策略的电流纹波有效值的时域表达式。通过比较，最终选取性能较优的调制策略，并推导出相应的统一调制波表达式，只需简单地对参考电压进行四则运算并与载波进行比较，即可得到各开关管的开通、关断时刻，避免了复杂的扇区选择过程和三角函数运算，有效减轻了数字控制器的实时运算负担。

1 容错型四开关逆变器空间矢量调制

常用的容错型三相逆变器拓扑如图1所示，直流侧电容C1和C2的中性点通过3个双向晶闸管分别与三相输出端相连，C1和C2的电压分别为UDC1和UDC2，n为交流负载中性点。每相桥臂上与2个快速熔断丝串联，当逆变器某相功率器件发生故障时（本文中以a相为例），断开故障桥臂，同时控制相应的双向晶闸管TRa开通，重构为三相四开关逆变器拓扑。

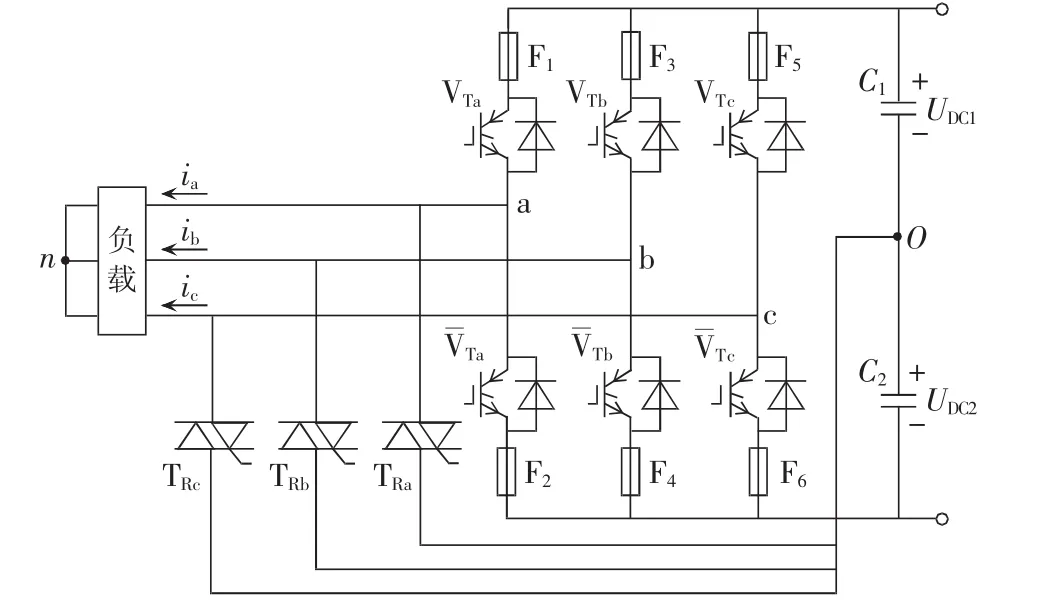
图1 容错三相四开关逆变器拓扑结构Fig.1 Topology of fault-tolerant three-phase four-switch inverter

从图中可以看出，故障后重构的四开关逆变器中，a相电流由电容中性点流出，上下两电容的容值一般是相等的，即C=C1=C2，则有：

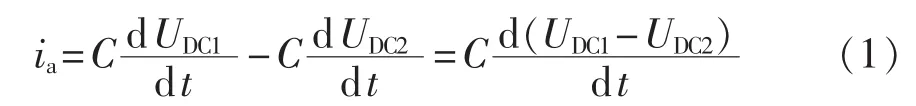
对式（1）两边同时积分，则有：

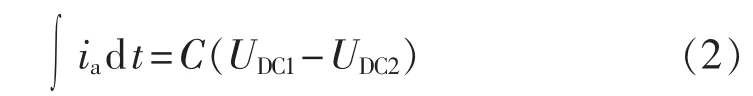
设 ia=Imcos（ωt+φ），则式（2）可以化为：

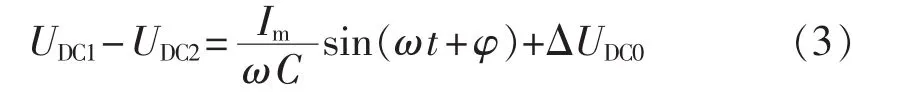
其中，ΔUDC0为两电容初始电压差值。由式（3）可以看出，电容电压以负载电流的频率随时间波动，且波动幅度与电流幅值、频率及电容值相关。当电流幅值较大且频率较低时，电容电压波动的幅度也越大。

本文在分析三相四开关逆变器4个开关状态的输出电压时，考虑了上下电容电压不平衡的情况。根据图1的拓扑，由基尔霍夫电压定律，可以得到逆变器输出线电压的表达式为：

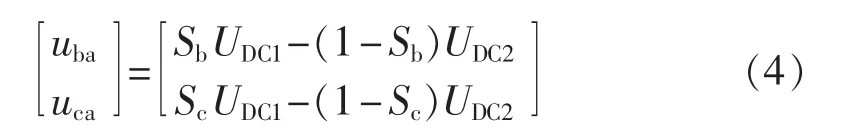
其中，Sb和Sc分别代表b、c两相桥臂的开关状态，值为1时代表上管开通、下管关断，值为0时代表上管关断、下管开通。将式（4）中线电压转换为相电压，则有：

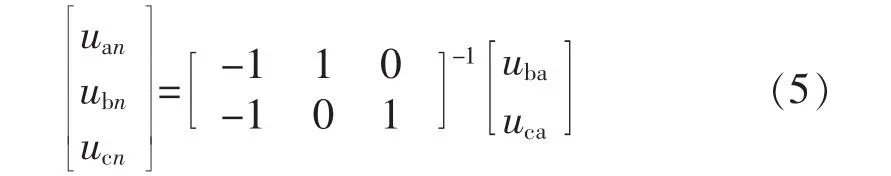
再将式（5）变换到αβ坐标系下，有：

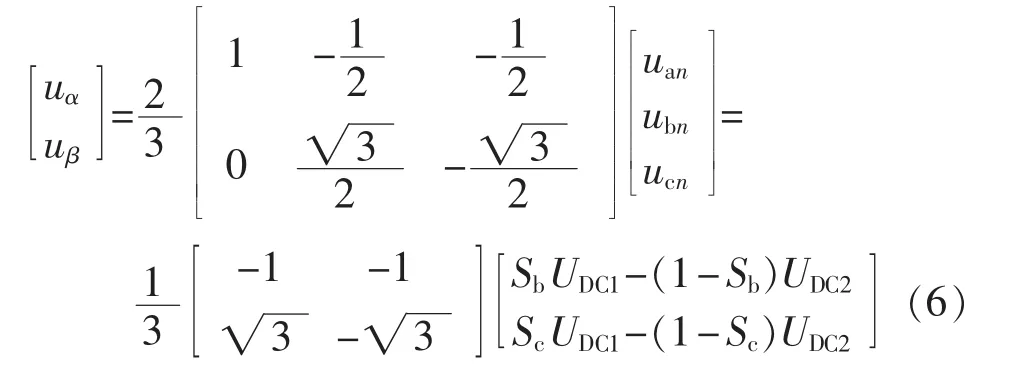
由式（6）可以得到三相四开关逆变器在αβ坐标系下的4个空间基本矢量坐标与开关状态的对应表如表1所示。

根据表1，将各基本矢量绘制在α-β平面上，4个基本矢量将矢量空间平面分隔为4个扇区，分别以Ⅰ、Ⅱ、Ⅲ、Ⅳ扇区对其进行命名，如图2所示（此时 UDC1＜UDC2）。由于上下两电容电压不平衡，U1和U3方向相反，幅值却不相等；U2和 U4幅值相等，方向却不相反。根据式（3），当电流幅值较大且频率较低时，电容电压波动较大，电压矢量的不对称程度也更明显。若不考虑电容电压波动的影响，仍简单地认为UDC1=UDC2，采用文献［8-11］中的方法计算各基本矢量的作用时间，逆变器输出电压矢量会与参考电压矢量存在差异，进而引起负载电流畸变。

表1 容错型四开关逆变器基本矢量表Table 1 Basic vectors of fault-tolerant four-switch inverter

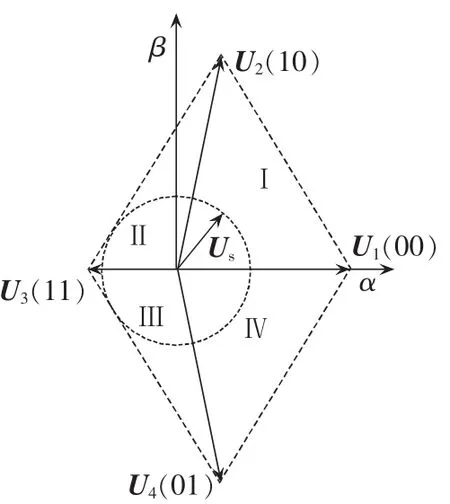
图2 容错型四开关逆变器基本矢量（UDC1＜UDC2）Fig.2 Basic vectors of faulttolerant four-switch inverter（UDC1＜UDC2）

由图2可知，三相四开关逆变器的基本矢量中并不包括零矢量，需要使用2个方向相反的基本矢量进行等效合成，获得零矢量的效果，而这2个基本矢量称为“劈零矢量”。一般而言，可以分别选择两短矢量U1和U3或选择两长矢量U2和U4作为劈零矢量，如图3所示。

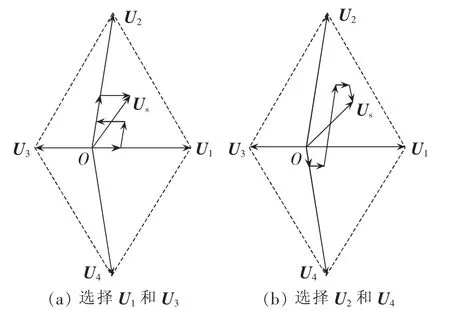
图3 选择不同劈零矢量合成参考矢量Fig.3 Two approaches of zero-vector synthesis

将选择U1和U3作为劈零矢量时的调制方法命名为SVM1调制方式。根据图2可以得到，在Ⅰ、Ⅱ扇区内，参考矢量Us是由邻近的3个基本矢量U1、U2和U3合成的，根据伏秒平衡原理，并结合表1中数据，可知各基本矢量作用时间为：

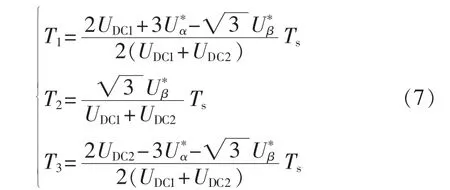
其中，分别为参考电压矢量Us在α、β轴的分量；Ts为开关周期。

当参考矢量Us位于Ⅲ、Ⅳ扇区时，选取邻近的3个基本矢量U1、U3和U4对参考矢量进行合成，各基本矢量的作用时间为：

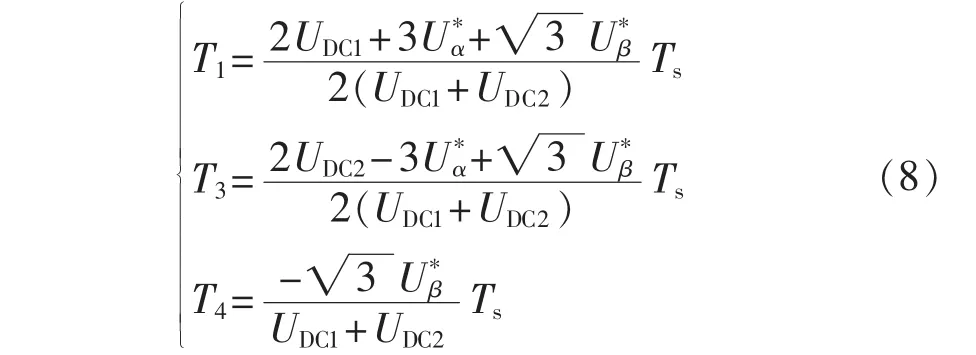
将选择U2和U4作为劈零矢量时的调制方式命名为SVM2调制方式。在Ⅰ、Ⅳ扇区内，参考矢量Us是由 U1、U2和 U4合成的，则有：

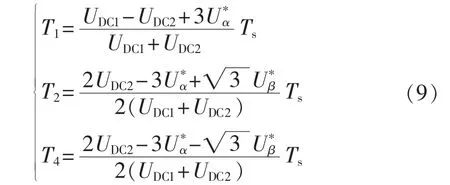
当参考矢量位于Ⅱ、Ⅲ扇区内时，选取U2、U3和U4对参考矢量Us进行合成，可以计算出各基本矢量的作用时间为：

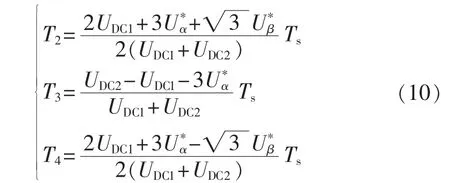
为了减少开关次数和抑制谐波，确定一个开关周期内空间矢量分布原则为：同一桥臂上的开关器件状态只改变2次；空间矢量按中心对称原则分布［21］。由上述原则，并结合2种不同调制方式时基本矢量的选取与作用时间，可以得到三相四开关逆变器一个开关周期内的空间矢量调制电压输出波形如图4所示。

2种不同的零矢量合成方法产生了不同的PWM电压输出波形，对逆变器的输出性能也会带来不同影响，所以需要对调制方式的性能进行评估，在实际应用中选择性能更好的调制方式。

2 不同调制方式的性能评估

理想状态下，三相四开关逆变器的交流负载侧电路方程可以表示为：

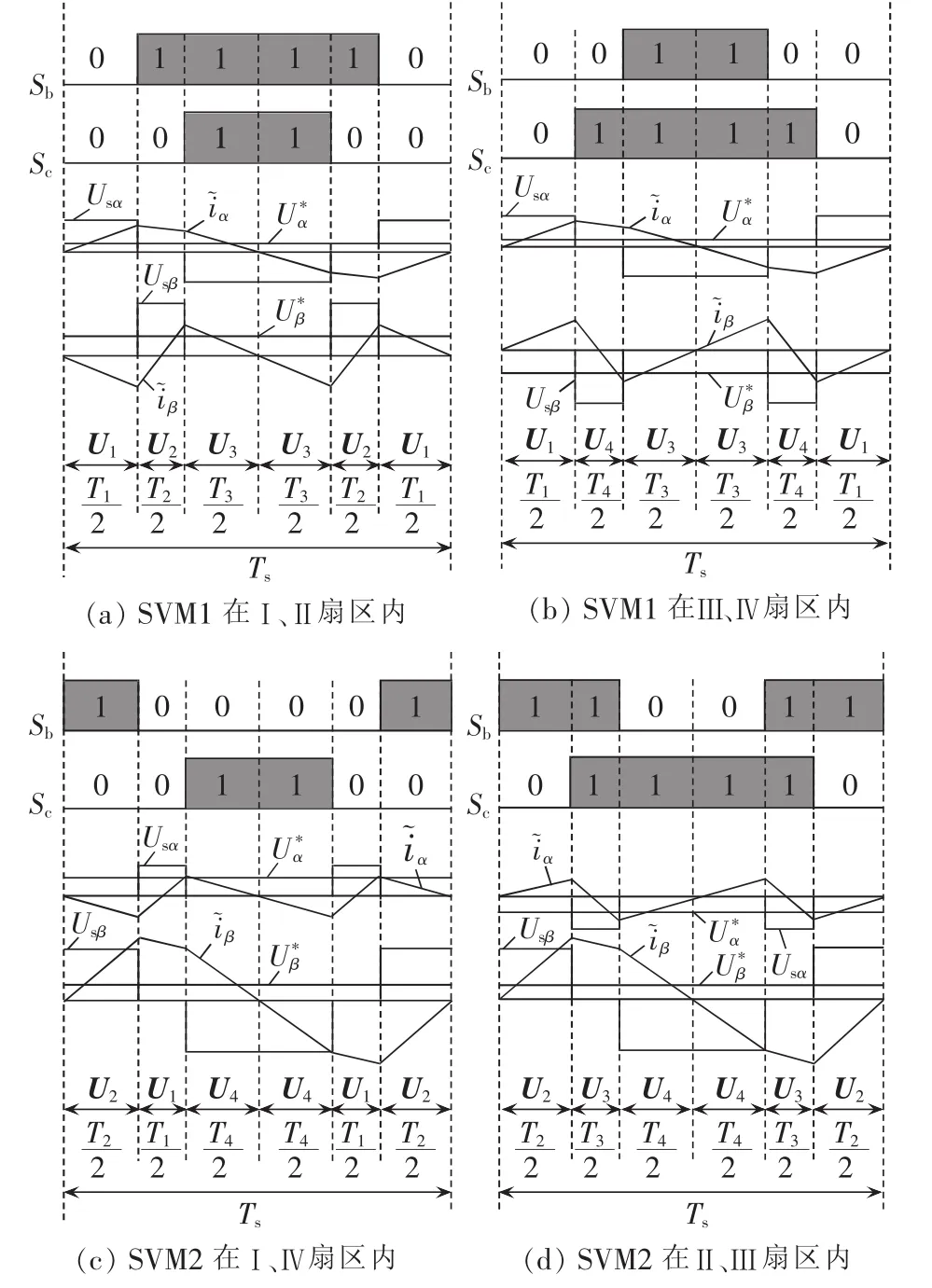
图4 四开关逆变器开关序列及电流纹波Fig.4 Switching sequences of four-switch inverter and corresponding ripple currents

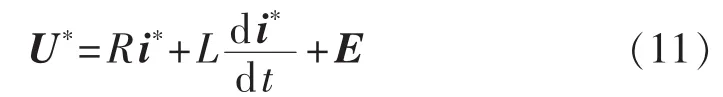
其中，E为电机的反电动势，若只考虑阻感负载，则认为E=0；U*和 i*分别为参考电压矢量和期望电流矢量。考虑到在空间矢量调制中，一个开关周期内的逆变器输出电压矢量Us的平均值与参考电压矢量U*相等，但Us的瞬时值只是空间上离散的几个逆变器的基本矢量，与U*有所差异，即：

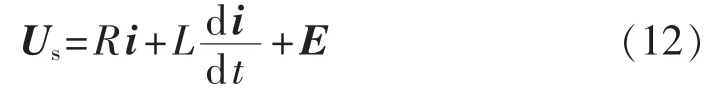
其中，i为实际电流，其与期望电流矢量i*并不完全一致，而是存在一定的纹波分量。可以定义纹波电压和纹波电流如下：

根据式（11）—（13），同时忽略电阻的影响，可以得到电流纹波的表达式如下：

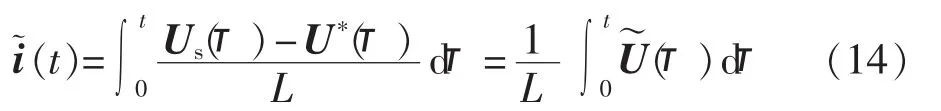
在三相四开关逆变器中，由于使用不同的零矢量合成方式，电流纹波值也会不同，如图4所示。为了定量分析比较不同调制方式的电流纹波性能，可以将式（14）中电流纹波矢量的幅值定义为三相电流纹波值，其计算方法如下：

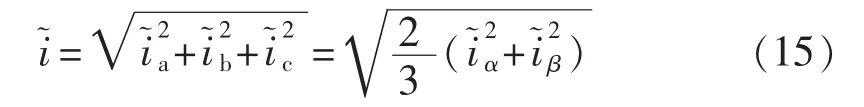
其中，α和β分别为静止坐标系下电流纹波的α、β轴分量。由图4可以看出，在空间矢量调制中，每个开关周期内矢量分布是对称的，所以电流纹波的幅值也呈奇对称分布，只需对半个周期内的电流纹波值进行积分计算，便可以得到整个开关周期内的有效值：

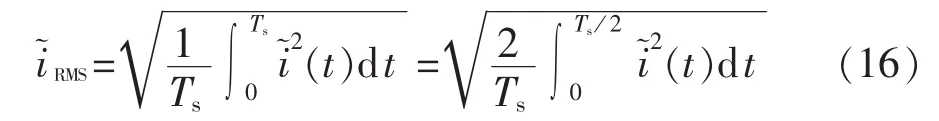
为计算电流纹波有效值，首先需要推导电流纹波幅值的表达式。以采用SVM1调制方式时参考电压矢量位于Ⅰ、Ⅱ扇区为例，电流纹波幅值为：

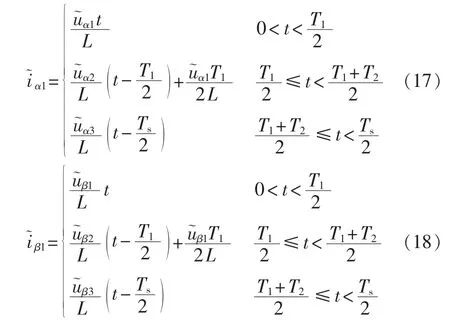
其中，为纹波电压的 α、β 轴分量，即参考电压矢量与参与合成的基本电压矢量α、β轴分量之差。为了简化分析，可以认为电容中性点电压是平衡的，即UDC1=UDC2=UDC/2。同时，为了更好地说明参考电压矢量幅值和相位对电流纹波的影响，可以令：

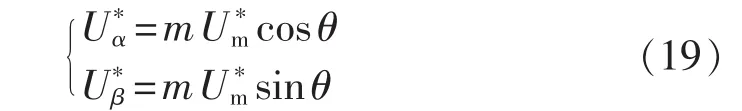
其中，mϵ［0，1］为调制度；为参考电压所能达到的最大幅值；θ为参考电压矢量的空间角度。结合式（15）—（19），并参考表1中基本电压矢量在 α、β轴上的幅值分量以及式（7）、（8）中各基本矢量的作用时间，可以计算出采用SVM1调制方式时，电流纹波在一个开关周期内的有效值为：

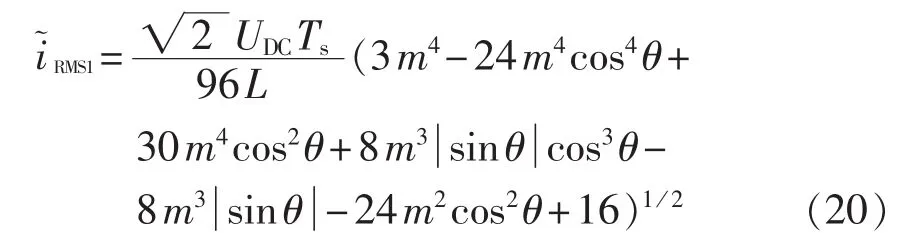
采用SVM2调制方式时，在Ⅰ、Ⅳ扇区和Ⅱ、Ⅲ扇区所选取的基本电压矢量不同，用上述方法，同样可以推导出其电流纹波在一个开关周期内的有效值的表达式为：

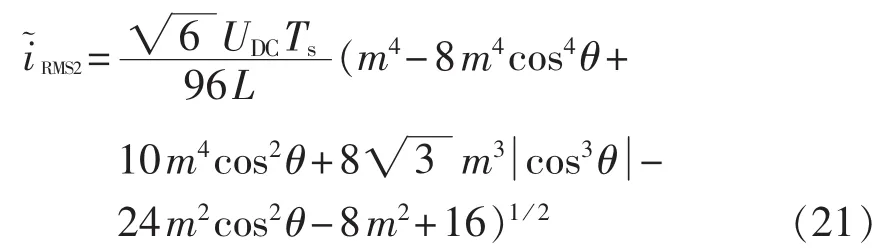
从式（20）和（21）中可以看出，当母线电压 UDC、电感L、开关周期Ts不变时，一个开关周期内的电流纹波有效值与参考电压矢量的空间角度和幅值（调制度）有关。将2种调制方式的电流纹波有效值（标幺值）绘于图5中，通过比较可以看出，在一个开关周期内，无论参考电压矢量的幅值与角度如何变化，即参考电压矢量处于α-β平面的任何位置，采用SVM2调制方式的电流纹波有效值均要比采用SVM1调制方式的高。

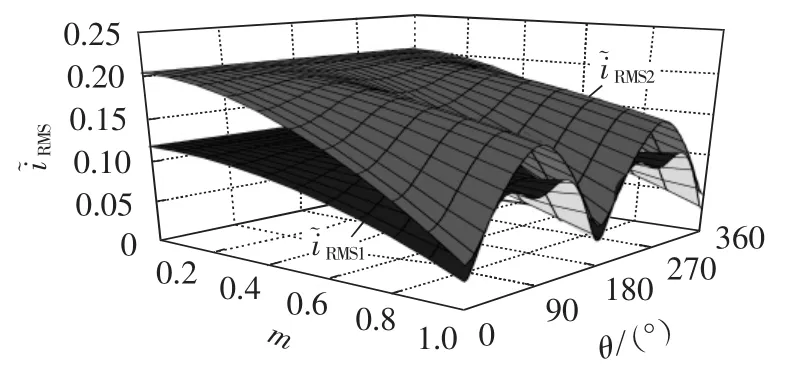
图5 使用不同调制方式时电流纹波在一个开关周期内的有效值Fig.5 Effective ripple current in one switching period for two modulation approaches

为了进一步分析，从基波周期的角度出发，使用式（22）计算一个基波周期内的电流纹波有效值。

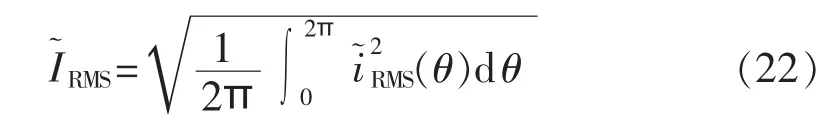
将式（20）、（21）代入式（22）计算，可以得到 2 种调制方式在一个基波周期内的电流纹波有效值分别为：

将2种调制方式的电流纹波有效值（标幺值）绘于图6中。通过比较可以看出，当调制度较低（0＜m＜0.3）时，2种调制方式的电流纹波有效值均比较大，且采用SVM2调制方式的电流纹波有效值接近采用SVM1调制方式时的2倍；随着调制度的提高，2种调制方式的电流纹波有效值均开始减小；当调制度较高（0.9＜m＜1）时，2种调制方式下的电流纹波有效值比较接近，但采用SVM1方式的仍比采用SVM2方式的要低。从以上分析中看出，调制度是影响三相四开关逆变器电流输出品质的重要因素，实际应用中应在能满足线性调制输出的条件下尽量降低直流母线电压来提高调制度，以获取更好的调制输出性能。同时，使用SVM1调制方式，可以在全调制范围内获得更优良的电流输出品质，所以在实际应用中应优先选择这一调制方式。

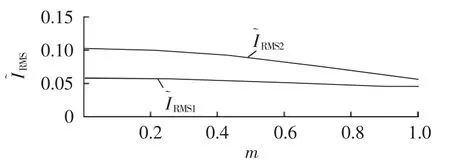
图6 一个周期内的电流纹波有效值比较Fig.6 Comparison of effective ripple current in one period between two approaches

3 四开关逆变器空间矢量载波调制实现方案

根据以上分析，容错型四开关逆变器采用U1和U3作为劈零矢量（SVM1调制方式）时，可以使输出电流纹波更小、性能更佳。因此，在实际应用中，应该选取SVM1调制方式，以尽量缩小故障后输出电流性能与故障前的差距。结合图4中的矢量排布方式，可以得到当参考矢量Us在Ⅰ、Ⅱ扇区时，每个开关周期内b相和c相桥臂上管开通时间为：

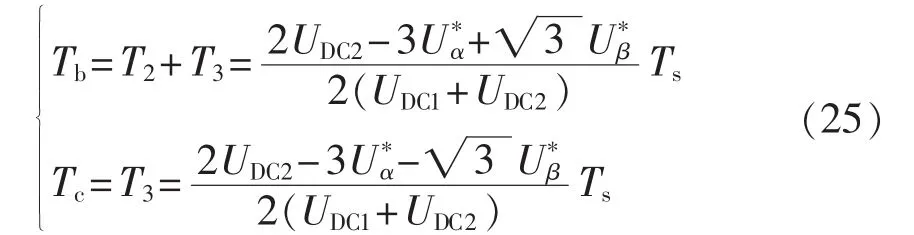
同理可得，参考矢量Us在Ⅲ、Ⅳ扇区时，每个开关周期内b相和c相桥臂上管开通时间为：

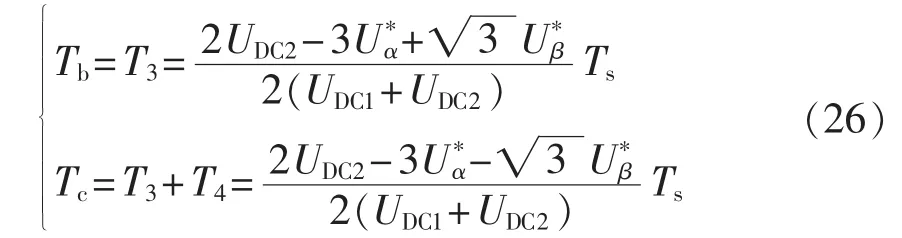
根据式（25）、（26）可以看出，参考矢量 Us的位置并不影响各开关管的占空比。在实际应用中，如果直接使用式（25）、（26）计算 b、c 相开关的开通时间，还需进行坐标变换，同时上述表达式中还存在无理数的运算，所以考虑对其作进一步的化简。可以将上述表达式中αβ坐标系下的参考电压分量转化为三相静止坐标系下的分量，得到：

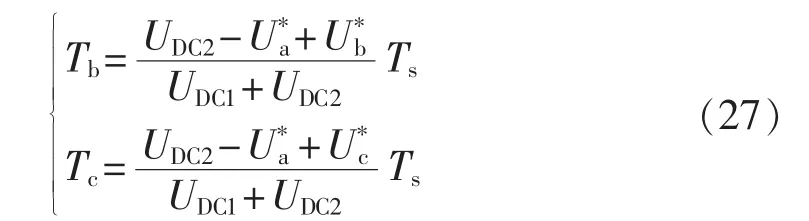
根据式（27），可以通过对三相参考电压值以及直流母线两电容电压值进行简单的四则运算，直接得到b、c两相开关管的占空比。将式（27）结果作为调制波，与载波进行比较（如图7所示），可以直接得到每个开关器件的开通、关断时刻，无需判断扇区，避免了复杂的三角函数运算。同时，使用式（27）计算调制波，可以对电容中性点电压波动进行补偿，消除输出电流畸变。表2中列出了文献［12-15］中传统调制算法与本文提出的基于载波的空间矢量调制算法的计算量比较，可以看出本文提出的调制算法有效减少了计算量，对提高数字控制器的控制实时性、降低电流品质恶化比较有利。

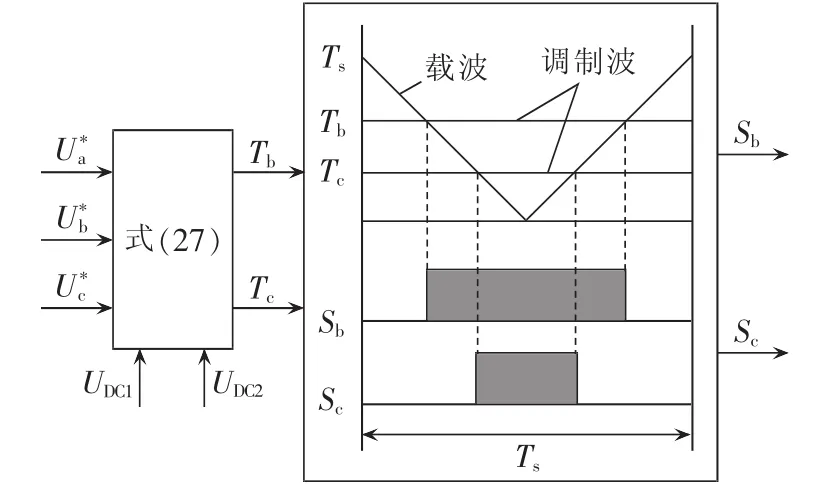
图7 四开关逆变器载波调制实现方案Fig.7 Implementation of carrier-based modulation for four-switch inverter

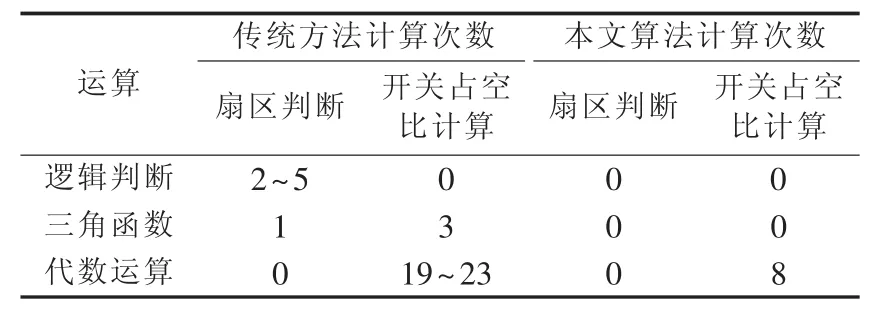
表2 调制算法计算量比较Table 2 Comparison of computational complexity between two modulation algorithms

4 实验验证

为验证本文所提基于载波调制的容错型三相四开关逆变器空间矢量调制优化算法的有效性，搭建了实验平台进行实验验证。其中，IGBT模块采用Semikron公司的SKM200GB12V；控制器采用TI公司的TMS320F2808定点DSP芯片；直流母线电压为400 V，直流侧电容C1=C2=2400 μF；交流侧负载为阻感性负载，电阻值为6 Ω，电感值为3 mH；输出电流基频为50 Hz；开关频率为10 kHz。

图8为传统调制算法（未考虑电容中性点波动）与本文提出的载波调制补偿算法的输出电流及其在静止坐标系下的轨迹。受电容电压波动的影响，三相四开关逆变器的基本空间电压矢量是不平衡的。采用传统调制算法时，输出电压矢量未得到合适的补偿，逆变器输出电压是不平衡的，因此输出电流畸变较为明显；而采用本文提出的补偿算法时，逆变器输出三相电压不受电容电压波动影响，仍然是平衡的，因此输出三相电流也是平衡的。对比采用2种调制算法时输出电流在α-β平面的轨迹，可以看出采用补偿算法的电流轨迹更接近“正圆”，进一步验证本文所提补偿调制算法可以抑制电容中性点电压波动对输出电流畸变的影响。

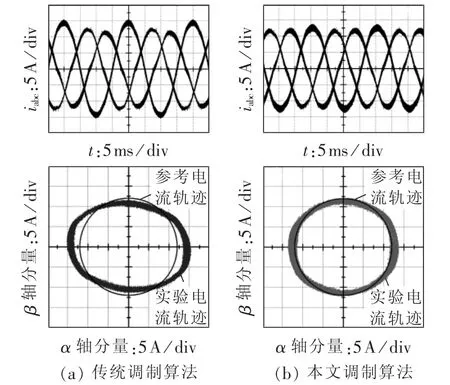
图8 未采用和采用补偿调制算法的输出电流实验波形Fig.8 Experimental output currents of modulation algorithm without and with compensation

图9为调制度m=0.5时，分别采用2种不同零矢量合成方式时输出电流及纹波。当采用SVM1调制方式时，可以看出三相电流的纹波较为均衡；而采用SVM2调制方式时，故障相（a相）电流纹波较小，而另两相电流纹波较大。通过式（15）计算出三相电流纹波值，比较发现，SVM1调制方式的电流纹波值比SVM2调制方式的更小。

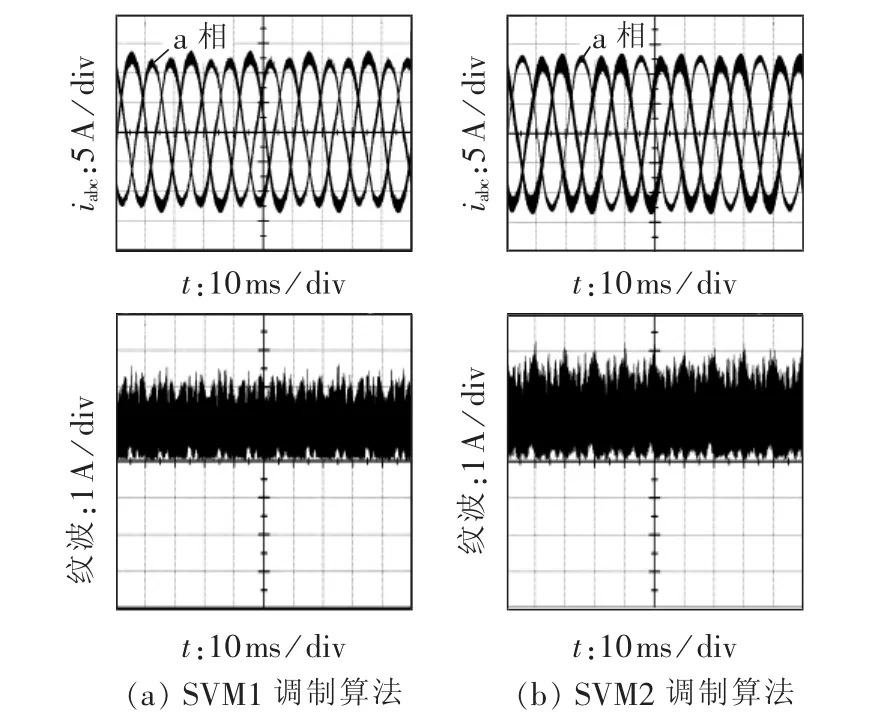
图9 采用SVM1和SVM2调制算法时的输出电流实验波形Fig.9 Experimental output currents of modulation algorithm SVM1 and SVM2

为进一步说明问题，在线性调制区域内改变调制度，并计算出2种调制方式在基波周期内的电流纹波有效值，如图10所示。由图10可见，实验结果基本与理论值相符，证明本文中提出的电流纹波有效值计算方法的正确性；同时，也证明采用SVM1调制方式可使电流输出品质更佳。

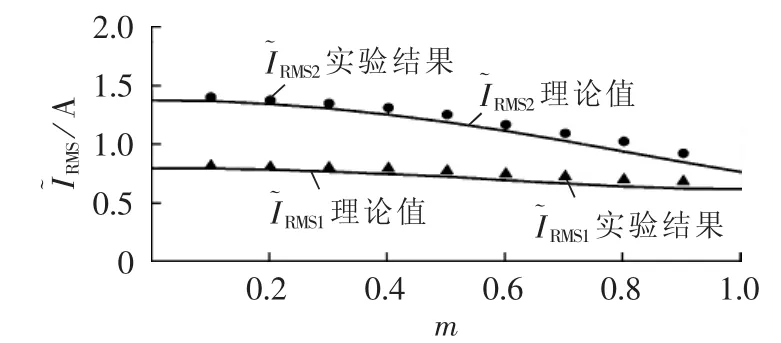
图10 2种调制方式电流纹波有效值实验结果Fig.10 Comparison of experimental effective ripple current between two modulation approaches

5 结论

本文首先分析了容错型三相四开关逆变器母线中性点电压波动的原因，以及其对电压基本空间矢量的影响。针对传统调制算法中未考虑中性点电压波动而产生的输出电流畸变现象，提出一种基于载波调制的空间矢量调制简化补偿算法，可以有效地抑制输出电流不平衡，同时避免了传统算法中复杂的三角函数计算以及扇区判断，减轻了控制器的计算负担，缩短了数字控制延时。对由于等效零矢量合成方法不同而产生的2种开关序列进行对比分析，采用电流纹波有效值作为评估标准，并推导出其在时域中的解析表达式，得出结论：输出电流品质随调制度提高而提高；采用两短矢量合成零矢量可以获取更优良的电流输出品质。

参考文献：

［1］YANG S，BRYANT A，MAWBY P，et al.An industry-based survey of reliability in power electronic converters［J］.IEEE Transactions on Industry Applications，2011，47（3）：1441-1451.

［2］魏书荣，黄苏融，符杨，等.永磁同步电机及其驱动系统故障处理与容错机制研究综述［J］.电力自动化设备，2016，36（10）：100-107.WEIShurong，HUANG Surong，FU Yang，etal.Overview on fault disposal and fault-tolerance mechanism of PMSM and its driving system［J］.Electric Power Automation Equipment，2016，36（10）：100-107.

［3］WELCHKO B A，LIPO T A，JAHNS T M，et al.Fault tolerant three-phase AC motor drive topologies：a comparison of features，cost，and limitations［J］.IEEE Transactions on Power Electronics，2004，19（4）：1108-1116.

［4］JACOBINA C B，BELTRAO DE ROSSITER CORREA M，LIMA A M N，et al.AC motor drive systems with a reduced-switchcount converter［J］.IEEE Transactions on Industry Applications，2003，39（5）：1333-1342.

［5］张兰红，胡育文，黄文新.容错型四开关三相变换器异步发电系统的直接转矩控制研究［J］.中国电机工程学报，2005，25（18）：140-145.ZHANG Lanhong，HU Yuwen，HUANG Wenxin.Researchon direct torque control of tolerant type four-switch three-phase converterinduction generation system［J］.Proceedingsofthe CSEE，2005，25（18）：140-145.

［6］FREIRE N M A，MARQUES CARDOSO A J.A fault-tolerant direct controlled PMSG drive for wind energy conversion systems［J］.IEEE Transactions on Industrial Electronics，2014，61 （2）：821-834.

［7］FREIRE N M A，MARQUES CARDOSO A J.A fault-tolerant PMSG drive for wind turbine applications with minimal increase of the hardware requirements［J］.IEEE Transactions on Industry Applications，2014，50（3）：2039-2049.

［8］BLAABJERG F，FREYSSON S，HANSEN H H，et al.A new optimized space-vectormodulation strategy fora componentminimized voltage source inverter［J］.IEEE Transactions on Power Electronics，1997，12（4）：704-714.

［9］安群涛，孙醒涛，赵克，等.容错三相四开关逆变器控制策略［J］.中国电机工程学报，2010，30（3）：14-20.AN Quntao，SUN Xingtao，ZHAO Ke，et al.Control strategy for fault-tolerant three-phase four-switch inverters［J］.Proceedings of the CSEE，2010，30（3）：14-20.

［10］王果，周末，常文寰.适用于高速铁路的三相四开关型滤波器的电流重复控制设计［J］.电力自动化设备，2016，36（2）：71-77.WANG Guo，ZHOU Mo，CHANG Wenhuan.Repetitive current control of three-phase four-switch APF for high-speed railway［J］.Electric Power Automation Equipment，2016，36（2）：71-77.

［11］郭镥，罗安，黎燕，等.新型光伏逆变器及其前馈功率预测控制［J］.电力自动化设备，2013，33（6）：119-123.GUO Lu，LUO An，LI Yan，et al.New photovoltaic inverter and itsfeedforward powerpredictive control［J］.Electric Power Automation Equipment，2013，33（6）：119-123.

［12］COVIC G A，PETERS G L.DC link imbalance compensation in four-switch inverter AC motor drives［J］.Electronics Letters，1997，33（13）：1101-1102.

［13］PETERS G L，COVIC G A，BOYS J T.Eliminating output distortion in four-switch inverters with three-phase loads［J］.IEE Proceedings-Electric Power Applications，1998，145（4）：326-332.

［14］BLAABJERG F，NEACSU D O，PEDERSEN J K.Adaptive SVM to compensateDC-link voltage ripple forfour-switch threephase voltage-source inverters［J］.IEEE Transactions on Power Electronics，1999，14（4）：743-752.

［15］BELTRAO DEROSSITER CORREA M，JACOBINA CB，CABRAL DA SILVA E R，et al.A general PWM strategy for four-switch three-phase inverters［J］.IEEE Transactions on Power Electronics，2006，21（6）：1618-1627.

［16］孙丹，何宗元，Blanco Ivonne Yznaga，等.四开关逆变器供电永磁同步电机直接转矩控制系统转矩脉动抑制［J］.中国电机工程学报，2007，27（21）：47-52.SUN Dan，HE Zongyuan，Blanco Ivonee Yznaga，et al.Torque ripple reduction for a four-switch inverter fed PMSM DTC system［J］.Proceedings of the CSEE，2007，27（21）：47-52.

［17］BECH M M，BLAABJERG F，PEDERSEN J K.Random modulation techniques with fixed switching frequency for three-phase power converters［J］.IEEE Transactions on Power Electronics，2000，15（4）：753-761.

［18］CASADEI D，SERRA G，TANI A，et al.Theoretical and experimental analysis for the RMS current ripple minimization in induction motor drives controlled by SVM technique ［J］.IEEE Transactions on Industrial Electronics，2004，51（5）：1056-1065.

［19］NARAYANAN G，RANGANATHAN V T.Analytical evaluation of harmonic distortion in PWM AC drives using the notion of stator flux ripple［J］.IEEE Transactions on Power Electronics，2005，20（2）：466-474.

［20］BASU K，PRASAD J，NARAYANAN G.Minimization of torque ripple in PWM AC drives［J］.IEEE Transactions on Industrial Electronics，2009，56（2）：553-558.

［21］HOLMES D G，LIPO T A.Pulse width modulation for power converters：principles and practice［M］.New York，USA：Wiley，2003：87.