Boost PFC变换器的动态斜坡补偿策略分析与设计

卢伟国，方慧敏，杨异迪，周雒维

（重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引言

功率因数校正 PFC（Power Factor Correction）变换器被广泛地应用于AC/DC整流装置，以实现输出电压的调节和高功率因数品质［1-4］。在大量的PFC变换器拓扑中［5-7］，工作在连续导电模式（CCM）下的Boost变换器是一类比较流行的主电路方案［8-9］。为了实现输入电流与输入电压同相，控制电路中常采用平均电流模式（ACM）和峰值电流模式（PCM）控制方案。而在峰值电流模式控制的Boost PFC变换器系统中，当占空比大于0.5时系统会出现次谐波振荡，因为在输入电流过零处占空比趋近1，系统必然存在次谐波振荡（快变）不稳定问题［10-11］，由此也会影响功率因数品质［12］。针对峰值电流模式存在的次谐波问题，工程设计中会同步引入斜坡补偿策略［13-15］以消除系统存在的次谐波振荡现象。但是，传统的斜坡补偿方式是通过降低电感电流的峰值以换取系统的稳定性［16］，因此电感电流的峰值包络线（即峰值）会偏离期望的正弦参考曲线，补偿强度过大则会造成偏离增大，进而引起电流畸变问题，尤其在电流过零处畸变更甚。由此带来的结果是，系统的总谐波畸变率（THD）和功率因数反而会比没有斜坡补偿时更糟糕。针对该问题，文献［17］提出全局斜坡动态补偿，通过动态补偿参考电流，解决了斜坡补偿过零死区问题，并且整个工频周期保持稳定，但补偿电流电路实现较为复杂，需要2片乘法器，成本较高。文献［18］基于前馈电流控制，通过电压过零检测补偿斜坡信号，增大电压过零时开关占空比，但控制效果一般。文献［19］采用谐振参数扰动法确定优化参数，但参数计算略繁琐且控制电路实现稍复杂，实验控制效果不是很理想。

针对斜坡补偿所存在的局限性，本文提出一种动态斜坡补偿方案，其实现电路简单。所提的动态斜坡补偿方案能有效抑制次谐波振荡，确保系统整个工频周期内的稳定性。同时补偿控制信号在开关切换时刻近似为零，即补偿信号不会改变电感电流的峰值，因此所提控制方案能有效改善斜坡补偿所存在的电感电流畸变问题，从而改善系统的功率因数品质。

1 问题描述及解决思路

峰值电流模式控制Boost PFC变换器系统如图1所示。图中，uac为理想的正弦交流输入电压，其幅值记为Um，即 uac=Umsin（ωLt），ωL为输入角频率；输入频率 fL和周期 TL满足 ωL=2πfL=2π/TL；整流后输入电压；输出电压为uo；系统的状态变量为电感电流iL和电容电压uC。峰值电流模式控制电路为双环结构，包括电压调节外环和电流调节内环，其中Uref为输出参考电压，CLK为周期为Ts的时钟信号，Δp为补偿控制信号，p1和p2分别为输入和输出的采样增益。电压调节外环由PI调节器和低通滤波器（LPF）组成［20］，其输出为内环的参考电流为叠加了补偿信号Δp后的补偿参考电流，即Δp。一般而言，电压外环的带宽会设计得很窄，从而获得内环的理想正弦参考，其中Re为等效的输入阻抗，幅值A≈Um/Re。

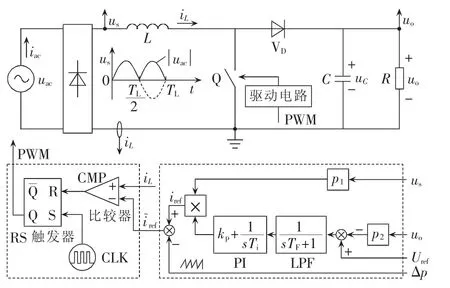
图1 峰值电流模式控制Boost PFC变换器原理图Fig.1 Schematic diagram of Boost PFC converter in PCM

1.1 斜坡补偿的问题及所提解决方案

图2（a）给出了无补偿的电感电流跟踪参考电流情形，即Δp=0，此时次谐波振荡行为不可避免地存在于电流过零处，因为过零处的系统占空比接近于1。图中 Tn=nTs，Tn+1=（n+1）Ts，Tdn=Tn+dnTs，dn为第n 个开关周期对应的占空比信号，Tdn为相应周期内的开关切换时刻。

参见图1的峰值电流控制模式，有，并且电感电流峰值iL（Tdn）等于补偿后的参考电流值。由此可得如下关系式：

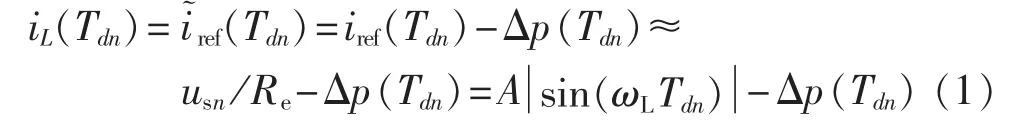
其中，usn=us（Tn）≈us（Tdn）。

图2（b）对应于斜坡补偿情形，此时Δp为：

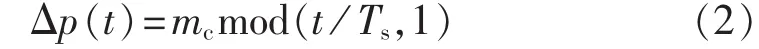
其中，mc为补偿强度。由式（1）和（2）可得：

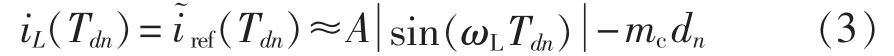
由式（3）可知，应用斜坡补偿时电感电流的包络线，即其峰值iL（Tdn）不再为期望的正弦波，这是由于存在附加补偿项 Δp（Tdn）=mcdn≠0。此外，这种畸变情形会在电流过零处更为严重，因为此时占空比dn接近于1，致使补偿信号Δp增大。当在过零点附近iref（Tdn）≤mc时，理论上参考电流小于零，但二极管的单向导电性使得电感电流iL只能维持零值，系统会出现过零死区，其死区范围会随着补偿强度mc增大而变大。

针对斜坡补偿存在的问题，本文提出了一种动态斜坡补偿思想，期望稳态补偿信号在开关切换时刻为零，即 Δp（Tdn）≈0。如此式（1）可变为iL（Tdn）≈，相应的补偿后电流情形如图2（c）所示。应用所提的动态斜坡补偿控制，电感电流峰值将被控制为期望的正弦波，即有 iL（Tdn）≈usn/Re≈。不难想象，系统过零处的电流畸变问题可以得到有效的改善，从而提高系统的功率因数品质。

图2 不同补偿形式下的电流波形Fig.2 Current waveforms of different compensation modes

1.2 被控电流的谐波畸变分析

因为，可通过对电感电流分析来分析输入电流，下面将从被控电感电流的平均值来分析系统的电流谐波畸变特性。在斜坡补偿方式下，图2（b）中的电感电流平均值iL1_av在半个输入工频周期内［0，TL/2］内可表示为：

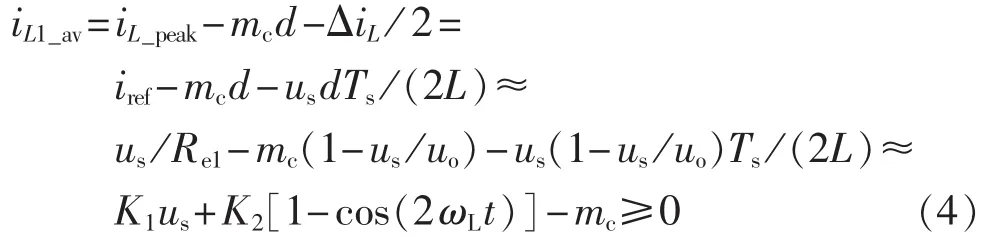
其中，ΔiL为电感电流纹波；d为占空比；Re1为斜坡补偿情形的输入阻抗；K1=1/Re1-Ts/（2L）+mcp2/Uref；。由式（4）可知，斜坡补偿方式下电感电流平均值过零处存在死区［0，t0］和［TL/2-t0，TL/2］，t0为临界时间点，满足 iL1_av（t0）≈0。如此，iL1_av可描述为：

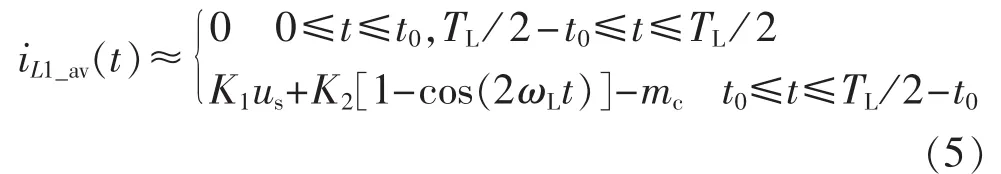
式（5）表明，斜坡补偿方式的引入会引起电流平均值的较大畸变，尤其是过零处，从而使得功率因数品质降低。同理，由图2（c）可知，所提动态斜坡补偿下的平均电感电流 iL2_av在［0，TL/2］内可描述为：

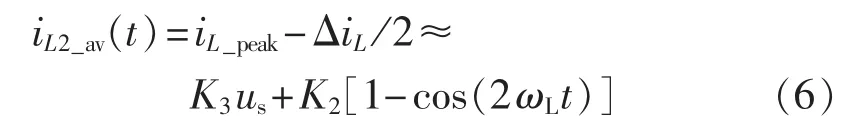
其中，K3=1/Re2-Ts/（2L），Re2为动态斜坡补偿下的等效输入阻抗。

对比式（4）和（6）可知，所提的动态斜坡补偿方式显然具有更好的补偿效果，式（6）中不存在（-mc）项，理论上表明不存在过零处畸变问题。

无论采用哪种补偿方式，系统均须满足在工频周期内的输入、输出平均有功功率平衡，即：

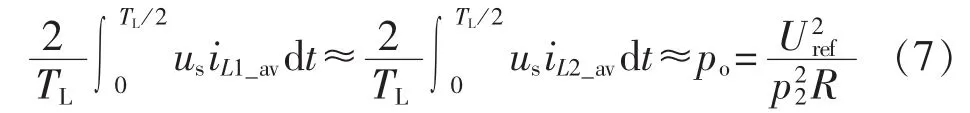
其中，po为相应的输出功率，可以认为恒定不变。由式（7）可以得到不同补偿方式下所对应的输入阻抗，即：

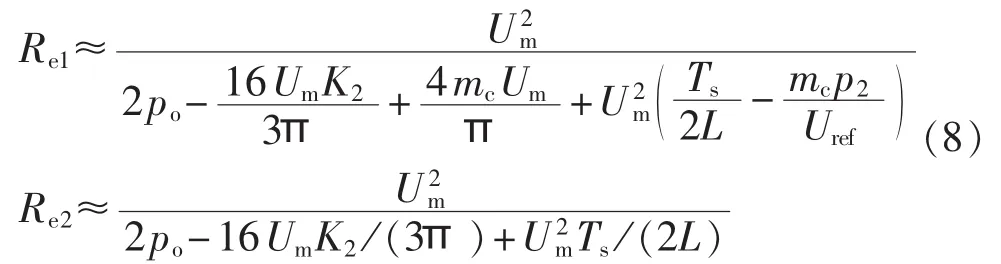
求解Re1过程中认为临界角（ωLt0）相比π小很多，此时 t0≈mc/（K1UmωL）。

结合式（4）、（6）和（8），应用傅里叶级数分解思想，并对临界角（ωLt0）作近似处理，可以得到斜坡补偿和所提动态补偿方式下所控输入电流平均值的谐波分解表达式为：

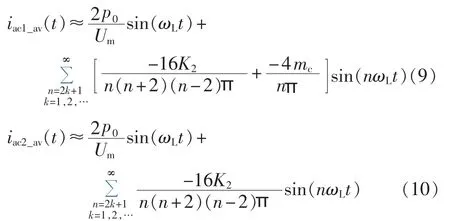
由式（9）和（10）可知，2种控制方法下基波分量相同，斜坡补偿下4mc/（nπ）谐波项正是由于斜坡补偿产生，动态斜坡补偿消除了该项的影响，从而减小了THD，提高了功率因数。

1.3 所提动态斜坡补偿的电路设计

根据1.1节中所述，所提的动态斜坡补偿必须满足设计条件Δp（Tdn）≈0，下面将以此设计条件给出相应的控制方程及电路设计。一般而言，系统开关频率远大于工频输入频率。因此一个开关周期内，系统可以近似看作为一个DC/DC Boost变换器，在第n 个开关周期满足准稳态关系 uon≈usn/（1-dn），其中usn=us（Tn）和 uon=uo（Tn）。基于前述，可设计出相应的动态斜坡补偿控制信号Δp为：

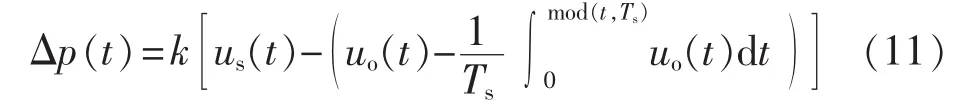
其中，k为比例增益。

依照式（11）所设计的控制方程，在第n个开关周期的切换时刻，有如下关系：

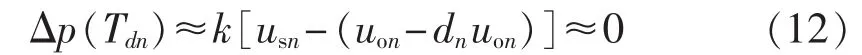
因此，所提动态斜坡补偿控制方程（11）满足前述的设计条件 Δp（Tdn）≈0。按照式（11）控制方程，相应的控制结构框图如图3所示，其电路仅仅需要简单运放和开关控制芯片实现。

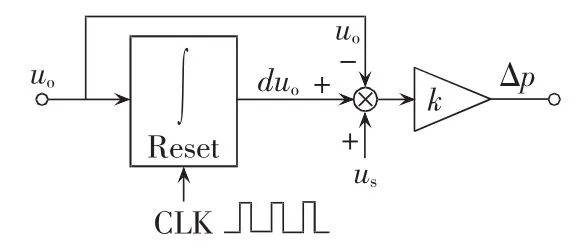
图3 动态斜坡补偿控制结构框图Fig.3 Control block diagram of DSC

1.4 稳定性分析及控制参数的确定

施加动态斜坡补偿的目的在于抑制系统的次谐波振荡，从而改善输入过零处的电流畸变。如此，可以通过对被控电感电流波形的稳定性分析，确定出动态斜坡补偿控制参数k的选取范围。施加了动态斜坡补偿的电感电流波形如图4所示。

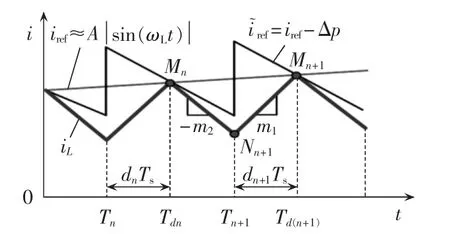
图4 动态斜坡补偿的电感电流波形Fig.4 Inductor current in DSC mode

由图中的第n和n+1个开关周期内Mn、Nn+1和Mn+1的依次迭代关系，可得如下方程：

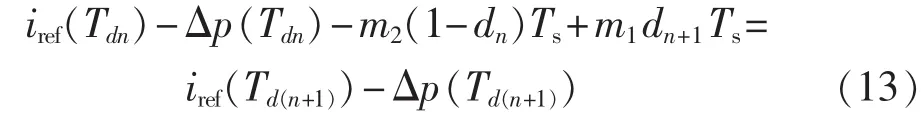
其中，m1=us/L 和 m2=（uo-us）/L 分别为电感电流上升和下降斜率。考虑到开关频率fs远高于输入电压频率fL，可认为在一个开关周期内iref近似不变，因此有 iref（Tdn）≈iref（Td（n+1））。此外输出电压近似满足 uo≈Uref，所以式（13）可以整理为：

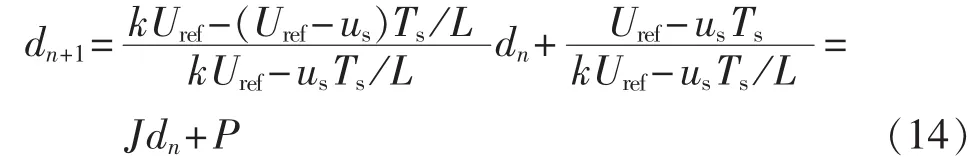
对式（14）进行线性化小信号扰动分析，设占空比 dn为dn=D+，其中 D 为稳态占空比，为扰动占空比。由式（14）可得小信号线性关系式。当时，系统能够保持稳定，即：

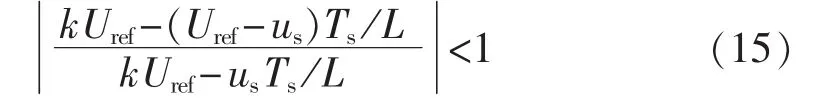
整理可得控制参数k的范围如下：

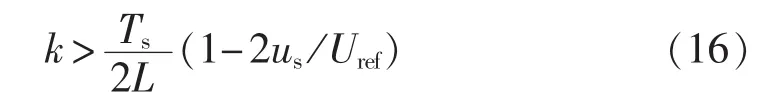
2 理论计算和仿真结果

系统电路参数选择如下：输入电压幅值Um=70V，参考电压Uref=3 V，开关频率fs=50 kHz，输入工频频率 fL=50 Hz，电感 L=2 mH，电容 C=470 μF，负载R=120 Ω，输入采样增益p1=0.1，输入反馈增益p2=0.02，低通滤波器时间常数TF=10 ms，PI的比例系数Kp=1，PI的时间常数Ti=20 ms，斜坡补偿强度mc=0.6，控制参数 k＞Ts/（2L）=0.005，本文选取 k=0.01。

具体理论计算与仿真对比结果如表1所示，其中理论结果由式（9）和（10）计算得到，需要说明的是谐波理论结果是基于输入电流的平均值得到，仿真计算结果基于电路仿真波形得到。此外仿真波形含有高频开关纹波分量，故仿真的THD值比理论THD结果略大。

此外，式（5）和（6）中的K2参数忽略了输出电压uo的波动，将其视为恒定Uref，由此造成平均输入电流3次谐波理论结果与仿真结果存在一定误差，如表1所示的3次谐波结果，从而也对最终的THD和功率因数产生影响。

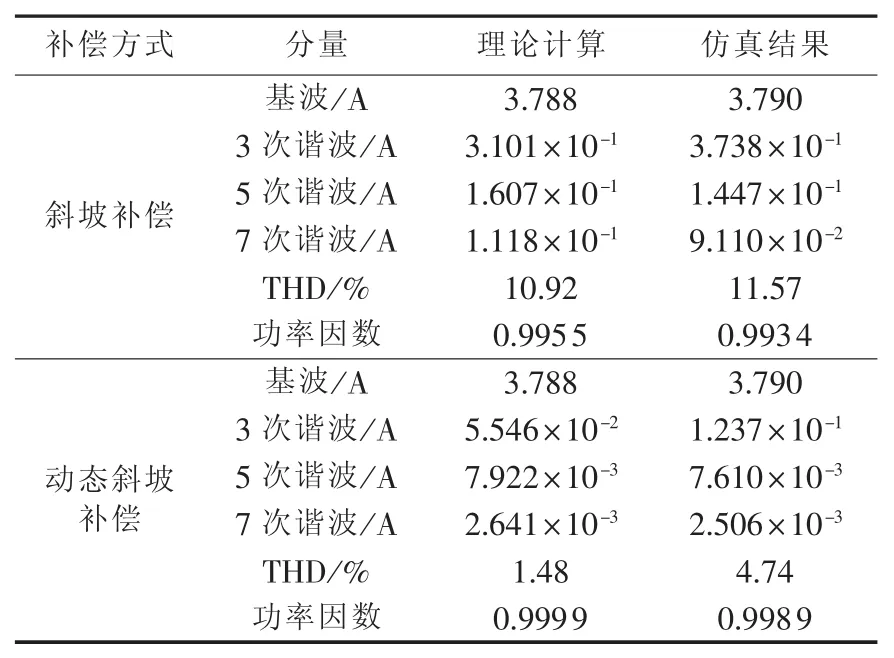
表1 理论与仿真结果Table1 Results of theoretical analysis and simulation

输入电流iac的理论平均结果iac_av及其仿真波形如图5所示。可以看出，2种补偿方式的理论平均值均接近仿真波形的平均值。图5（a）的斜坡补偿方式中，输入电流存在过零死区，临界时刻t0≈mc÷（K1UmωL）≈0.4468（ms），与图中仿真波形所显示结果相近。从图5（b）的所提动态斜坡补偿结果来看，所提补偿方式有效地解决了斜坡补偿中的输入电流的过零死区问题，使被控输入电流波形更接近理想正弦，有效改善了系统的功率因数品质。

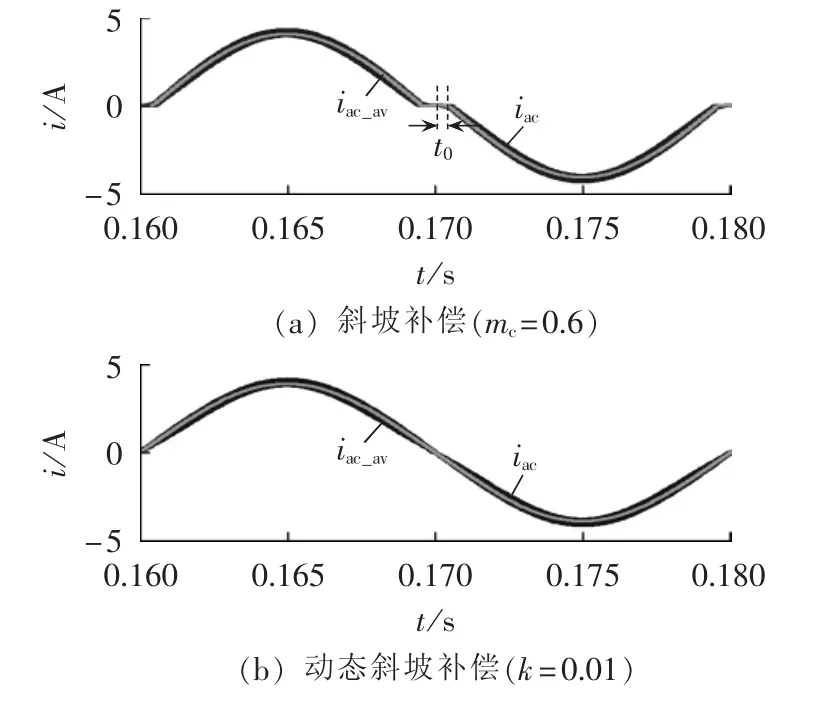
图5 斜坡补偿、动态斜坡补偿理论与仿真波形Fig.5 Theoretical and simulative waveforms of SC and DSC

3 实验结果

3.1 实验电路

系统实验电路参数与仿真参数一致，电感电流采样利用电流互感器LA25-NP实现，开关功率管及其驱动芯片型号分别为IRFP460和IR2110。所提动态斜坡补偿电路参照图3原理图构建，其中积分复位电路采用运放LF347和双向开关CD4016搭建。

3.2 实验结果

无补偿、斜坡补偿以及动态斜坡补偿的输入电压、输入电流以及其FFT结果如图6（a）—（c）所示。

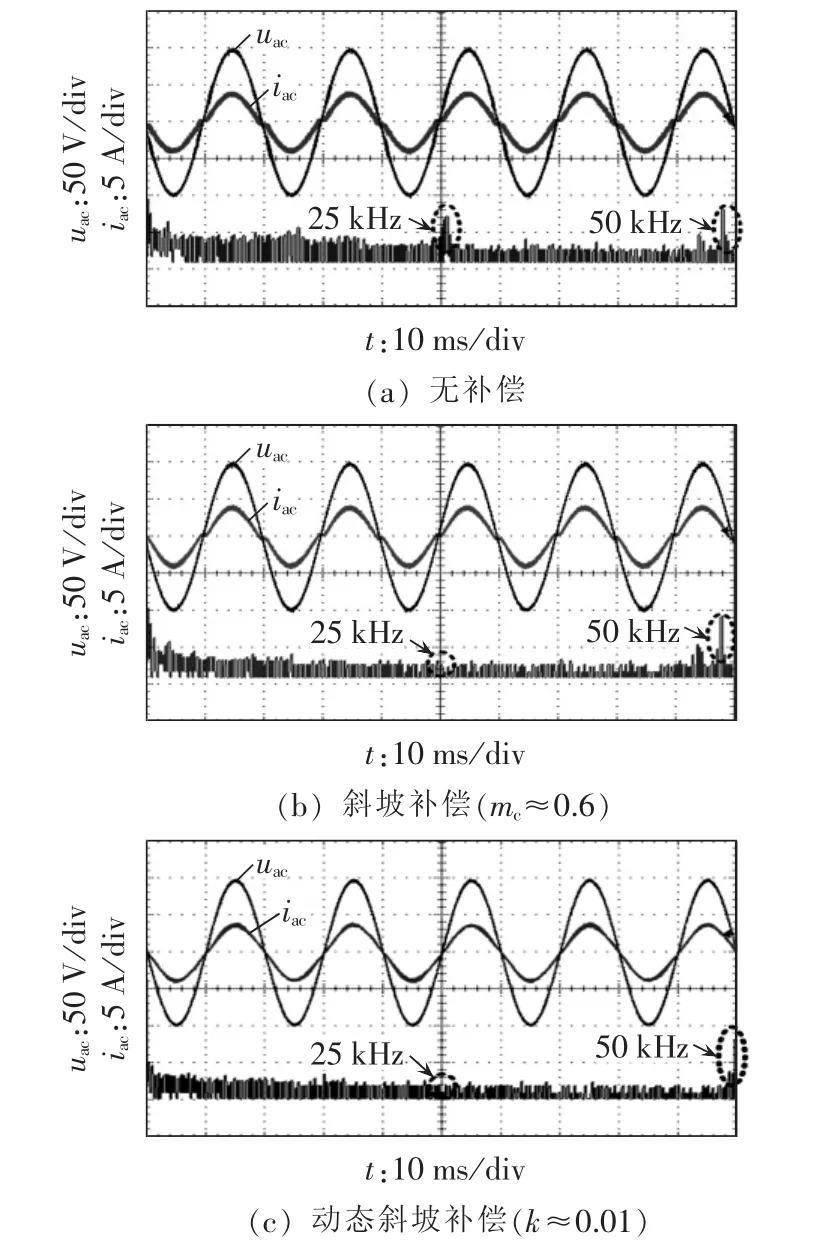
图6 无补偿、斜坡补偿和动态斜坡补偿时的输入电压、输入电流及其FFT结果Fig.6 Input voltage，input current and corresponding FFT for different compensation modes

从图6可知，3种情况下均能实现输入电流对输入电压的有效跟踪，从而保证系统的较高功率因数控制目的。此外，无补偿时系统存在明显的25 kHz次谐波分量，在应用了斜坡补偿和所提的动态斜坡补偿方式中，该25 kHz次谐波分量得到有效的抑制。

图7分别给出无补偿、斜坡补偿以及动态斜坡补偿3种情况下的输入电流实验波形及相应的THD及谐波分解结果。

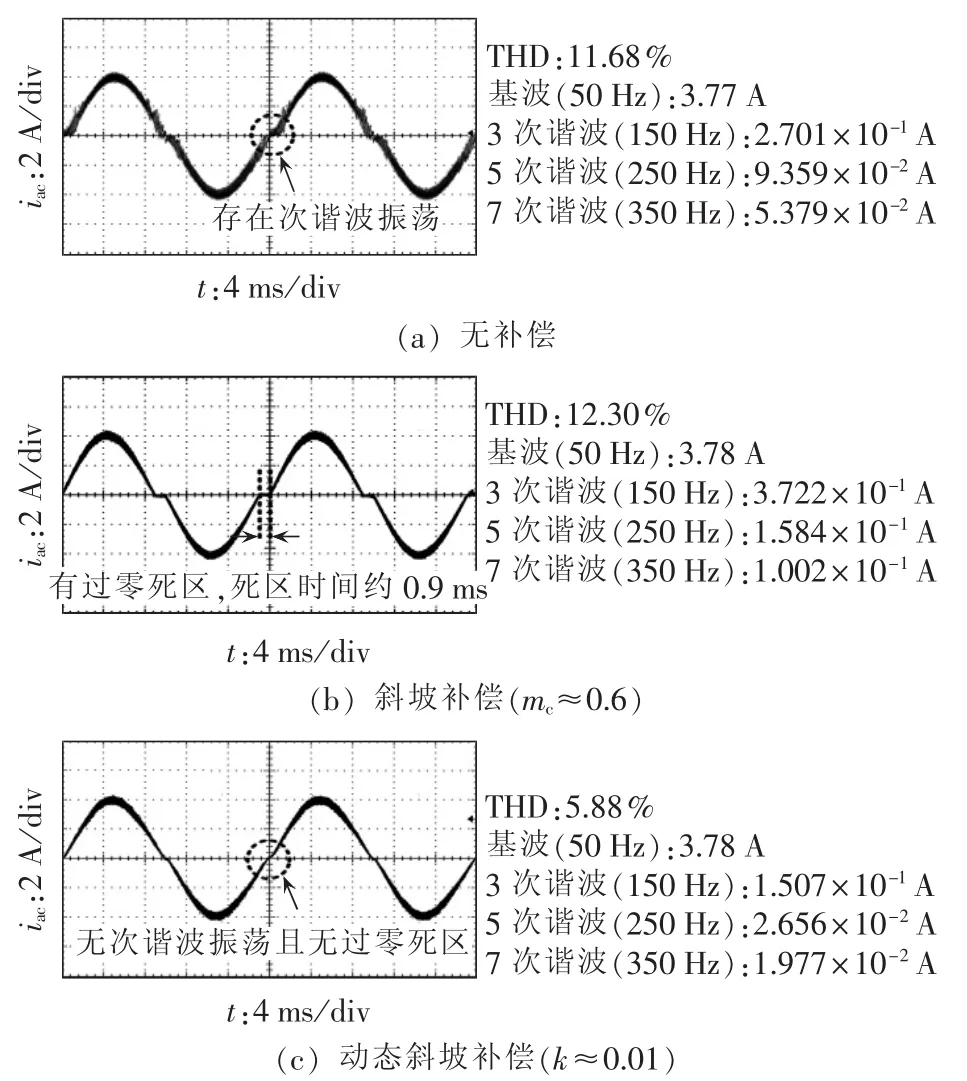
图7 无补偿、斜坡补偿和动态斜坡补偿时的输入电流Fig.7 Input current for different compensation modes

由图7可知，斜坡补偿会造成输入电流的过零死区，如图7（b）所示，实验死区时间约为0.9 ms，与理论值2t0≈0.89 ms比较接近，其THD为12.30%，比无补偿时的11.68%大；而所提的动态斜坡补偿可以有效改善斜坡补偿的输入电流过零畸变问题，其THD约为5.88%，对应的功率因数约为0.998。

4 结论

针对斜坡补偿的峰值电流模式Boost PFC变换器中所存在的电流畸变问题，本文提出一种动态斜坡补偿策略，有效地解决了斜坡补偿的电流过零死区问题，改善了THD，提高了系统的功率因数。此外，所提动态斜坡补偿保留了原有斜坡补偿的线性特点，电路实现简单。仿真与实验结果有效证明了所提动态补偿方案的有效性。

参考文献：

［1］TSE C K.Circuit theory of power factor correction in switching converters［J］.International Journal of Circuit Theory and Application，2003，31（2）：157-198.

［2］GARCIA O，COBOS J A，PRIETO R，et al.Single phase power factor correction：a survey［J］.IEEE Transactions on Power Electronics，2003，18（3）：749-755.

［3］SINGH B，SINGH B N，CHANDRA A，et al.A review of singlephase improved power quality AC-DC converters［J］.IEEE Transactions on Industrial Electronics，2003，50（5）：962-981.

［4］阎铁生，许建平，高建龙，等.低输出电压纹波准单级反激PFC变换器［J］.电力自动化设备，2015，35（9）：22-29.YAN Tiesheng，XU Jianping，GAO Jianlong，et al.Quasi singlestage flyback PFC converter with low output voltage ripple［J］.Electric Power Automation Equipment，2015，35（9）：22-29.

［5］WU X，TSE C K，DRANGA O，et al.Fast-scale instability of single stage power-factor-correction power supplies［J］.IEEE Transactions on Circuits System I：Regular Papers，2006，53（1）：204-213.

［6］郑连清，鲁思男.Boost PFC变换器快时标分岔的控制方法［J］.电力自动化设备，2013，33（10）：68-73.ZEHNG Lianqing，LU Sinan.Control of fast-scale bifurcation in Boost PFC converter［J］.Electric Power Automation Equipment，2013，33（10）：68-73.

［7］XIE X G，ZHAO C，ZHENG L W，et al.An improved buck PFC converter with high power factor［J］.IEEE Transactions on Power Electronics，2013，28（5）：2277-2284.

［8］姚凯，阮新波，冒小晶，等.电流断续模式Boost功率因数校正变换器的变占空比控制［J］.电工技术学报，2011，26（11）：14-24.YAO Kai，RUAN Xinbo，MAO Xiaojing，et al.DCM Boost PFC converter with variable duty cycle control［J］.Transactions of China Electrotechnical Society，2011，26（11）：14-24.

［9］王日文，曹文思，程立雪，等.Boost结构单周期控制的有源功率因数校正电路设计［J］.电力自动化设备，2011，31（12）：114-119.WANG Riwen，CAO Wensi，CHENG Lixue，et al.Design of Boost active power factor correction circuit with one-cycle control［J］.Electric Power Automation Equipment，2011，31（12）：114-119.

［10］马西奎，刘伟增，张浩.快时标意义下Boost PFC变换器中的分岔与混沌现象分析［J］.中国电机工程学报，2005，25（5）：61-67.MA Xikui，LIU Weizeng，ZHANG Hao.Analysis of fast-scale bifurcations and chaos phenomena in Boost PFC converter［J］.Proceedings of the CSEE，2005，25（5）：61-67.

［11］刘伟增，张浩，马西奎.基于频闪映射的Boost PFC变换器中的间歇性分岔和混沌现象分析［J］.中国电机工程学报，2005，25（1）：43-48.LIU Weizeng，ZHANG Hao，MA Xikui.Analysis of intermittent bifurcations and chaos phenomena in Boost PFC converters by stroboscopic map［J］.Proceedings of the CSEE，2005，25（1）：43-48.

［12］ORABI M，NINOMIYA T.Nonlinear dynamics of power-factorcorrection converter［J］.IEEE Transactions on Industrial Electronics，2003，50（6）：1116-1125.

［13］TIAN F，KASEMAN S，BATARSEH I.An adaptive slope compensation for the single-stage inverter with peak current-mode control［J］.IEEE Transactions on Power Electronics，2011，26（10）：2857-2862.

［14］CHEN W W，CHEN J F，LIANG T J，et al.Designing a dynamic ramp with an invariant inductor in current-mode control for an on-chip Buck converter［J］.IEEE Transactions on Power Electronics，2014，29（2）：750-758.

［15］何圣仲，许建平，周国华，等.谷值V2控制Boost变换器原理及稳定性分析［J］.电力自动化设备，2014，34（7）：21-27.HE Shengzhong，XU Jianping，ZHOU Guohua，et al.Principle and stability analysis of valley V2controlled Boost converter［J］.Electric Power Automation Equipment，2014，34（7）：21-27.

［16］ZHOU Y F，HUANG J C，WANG S B，et al.Principle of designing slope compensation in PFC Boost converter［J］.Science in China Series F：Information Sciences，2009，52（11）：2226-2233.

［17］程为彬，金金，郭颖娜，等.峰值电流型PFC Boost变换器斜坡补偿的时变模型和全局动态优化试验［J］.电子学报，2012，40（11）：2336-2341.CHENG Weibin，JIN Jin，GUO Yingna，et al.Time-varying ramp compensation mode and global dynamic optimization experiment of peak current control PFC Boost converter［J］.Acta Electronica Sinica，2012，40（11）：2336-2341.

［18］李娅妮，杨银堂，朱樟明，等.基于前馈电流控制斜坡补偿的Boost功率因数校正零交越失真研究［J］.电子与信息学报，2011，33（9）：2237-2242.LI Yani，YANG Yintang，ZHU Zhangming，et al.Design of zerocrossing distortion of Boost Power Factor Correction（PFC） based on feedforward current control slope compensation［J］.Journal of Electronics and Information Technology，2011，33（9）：2237-2242.

［19］雷涛，张晓斌，林辉.峰值电流控制的PFC变换器快时标分岔控制［J］.电工技术学报，2010，25（8）：91-98.LEI Tao，ZHANG Xiaobin，LIN Hui.Control of fast time scale bifurcations in PFC converters based on peak current control［J］.Transactions ofChina ElectrotechnicalSociety，2010，25（8）：91-98.

［20］刘斌，伍家驹，邹涛，等.基于比例谐振的PFC控制器及其单次谐波抑制［J］.电工技术学报，2011，26（7）：230-236.LIU Bin，WU Jiaju，ZOU Tao，et al.PFC controller design and selective harmonics compensation based on proportional-resonant［J］.Transactions ofChina ElectrotechnicalSociety，2011，26（7）：230-236.