浅谈分段函数的计算

岳红英

华北电力大学科技学院 河北保定 071051

在高等数学里有一类常见的函数，它的计算往往和一般的初等函数不同，稍有不慎就会出错，这就是分段函数。本文通过比较两种不同的求解方法对一元和二元分段函数在分段点出的求导问题进行了研究。

一、一元分段函数导数的计算

对于一般的初等函数求时往往用求导公式先求出导函数，则当然定义也是可行的，只是定义用起来通常比较麻烦。而分段函数因为在分断点两侧的函数表达式往往不同，所以其在分段点出有可能是不连续的，此时分段函数在分段点出一定不可导。即使分段函数在分段点出是连续的，但也不一定就可导，一般需用导数的定义或可导的充要条件即左右导数是否相等来判别其可导性。若直接用求出导函数代值（或求极限）的方法则有时会出错，本文通过以下实例对这两种方法进行了比较和研究，并给出了相应的结论。在分段点以外的开区间则常用初等函数的求导方法求出其导数。

例1讨论在和处的可导性，并求。

解法一

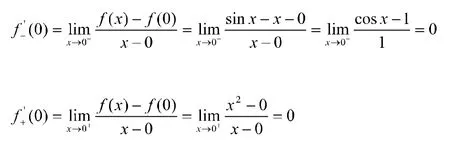
显然，所以在处可导且。

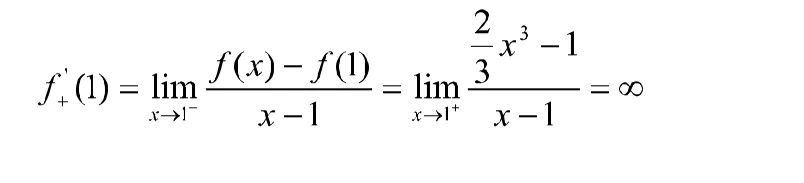
综上所述，即

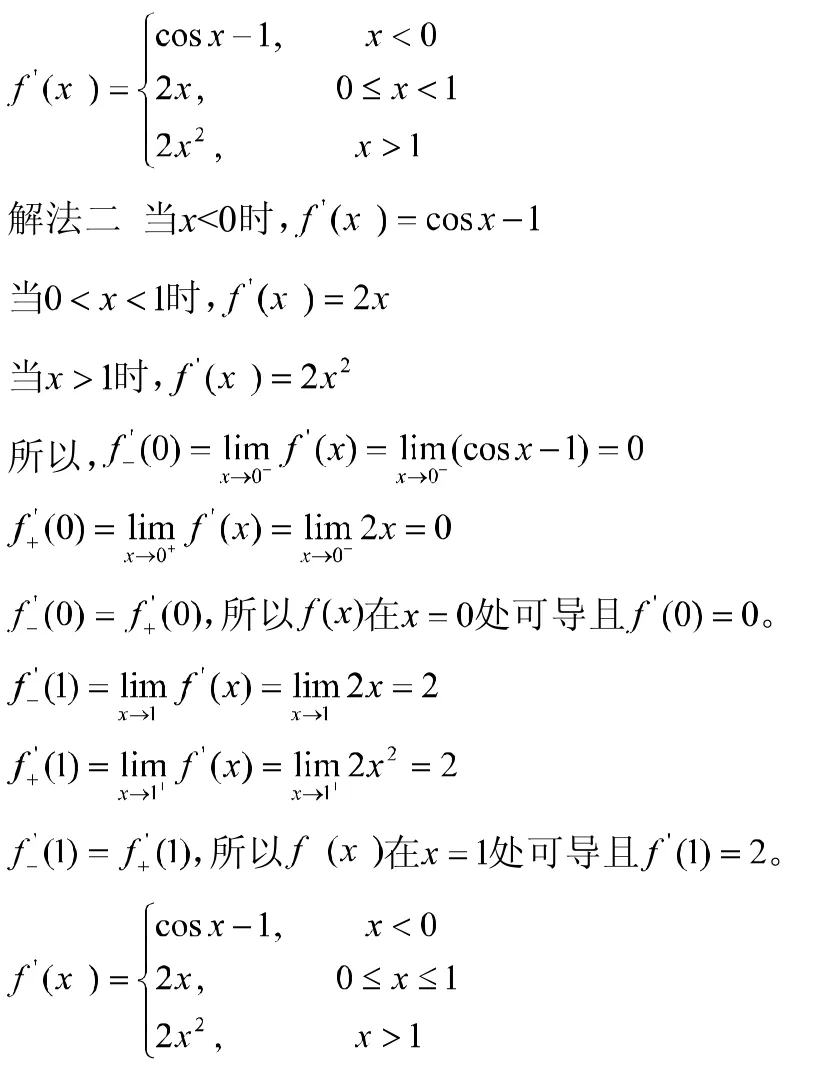
分析 解法一根据可导的充要条件即左右导数是否相等判断分段点处的可导性是正确的。解法二用导函数极限法求分段点处的左右导数求对了，而′1却判断错了，原因是在处是连续的，再求得分段点两侧导函数的极限相等，所以判断f x在x=0处是可导的。而在处不连续所以一定是不可导的，虽然和存在且相等，但导数f′1却不存在。所以使用导函数极限法求分段点处的导数时前提一定要先判断该点的连续性。

例2讨论函数在x=0处的可导性。

解法一 因为f x在两侧表达式相同，所以不用分别求左右导数，直接根据导数的定义讨论其在x=0处的可导性即可。

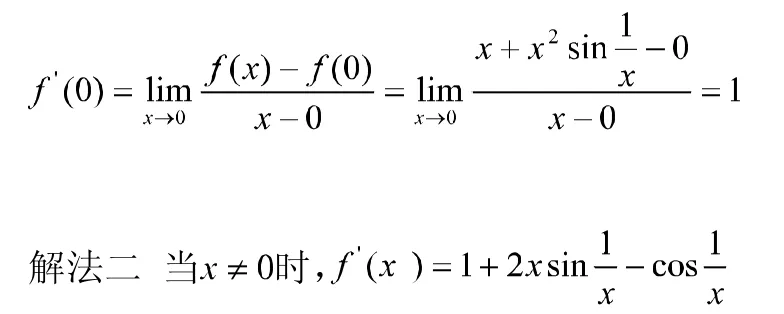
不存在，所以f x在x=0处不可导。

分析 解法二是错误的不存在，不能说明就不存在，这时只能用解法一也就是定义来判断分段点处的可导性。

通过以上两个例子的讨论可知，存在，右导数不一定存在，同样不存在，也不能说明就不存在。

二、多元分段函数的偏导数的计算

对一元函数来说，可导一定连续，不连续一定不可导，但在二元函数中这一关系不再成立，函数连续与偏导存在之间没有必然的联系，多元分段函数是一元分段函数的推广，多元分段函数在分段点处的偏导数的基本求法是定义，一般不用求出偏导函数再代值或求极限的方法。

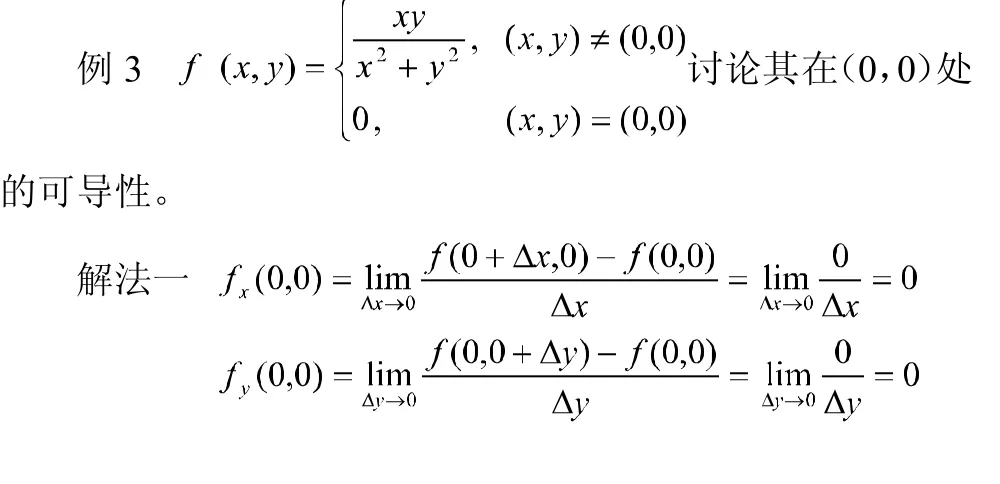
解法二 当时，

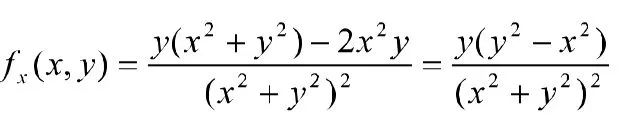
且不存在，所以不存在，同理不存在。

分析 解法二是错误的，和一元分段函数类似，多元分段函数在分段点处的偏导函数的极限不存在不能说明分段点处的偏导数值不存在，此时要用偏导数的定义来求。

三、结束语

通过上面几个例子的讨论，我们可总结出以下分段函数分段点处的求导方法：

（1）应用导数的定义或可导的充要条件求分段函数分段点处的导数是一种常用且不易

出错的方法，尤其对初学者是首选的好办法。当分段函数在分段点两侧表达式相同时就用导数的定义求分段点处的导数。当分段函数在分段点两侧表达式不同或者表达式虽然相同但含有一些比较特殊的左右极限不同的函数如等函数时则需用可导的充要条件即左右导数是否相等来判别其可导性。

（2）用导函数极限法求分段函数分段点处的导数时一定注意条件是否满足，只有当在上连续，在上 可 导，且（或）时，。且该条件乃是充分非必要的，若条件不满足则只能利用导数的定义或可导的充要条件来判断。

参考文献：

[1]同济大学数学系.高等数学（第七版）[M].北京:高等教育出版社,2014:78-84.

[2]华南理工大学数学系.高等数学教学辅导书[M].北京:高等教育出版社,2010:54-58.

[3]程黄金,陈伟.分段函数求导问题的多种解法[J].中国科技信息,2006,(16).

[4]刘其林,唐亮.一种分段函数分段点的求导方法及注意的问题[J].株洲师范高等专科学校学报,2007(4).

[5]刘秀丽,张长耀.分段函数有关问题的探究[J].佳木斯教育学院学报,2013(9).

[6]陈佩树.分段函数在分段点的求导[J].巢湖学院学报,2011(13).