线性聚能装药对自锻弹丸干扰的数值模拟
2017-05-18阮光光王凤英岳继伟石军磊
阮光光,王凤英,岳继伟,石军磊
(中北大学化工与环境学院,山西 太原 030051)
线性聚能装药对自锻弹丸干扰的数值模拟
阮光光,王凤英,岳继伟,石军磊
(中北大学化工与环境学院,山西 太原 030051)
为了研究线性聚能装药以不同角度干扰自锻弹丸的效果,采用有限元软件ANSYS/ls-dyna对线性聚能装药从不同角度(0°、30°、60°、90°)干扰自锻弹丸以及自锻弹丸被干扰后侵彻45号钢板的全过程进行数值模拟,然后运用Lsprepost后处理软件分析了自锻弹丸与聚能装药的射流头部在相遇前、相遇过程以及相遇后侵彻45号钢板过程中3个阶段的物理变化,通过分析对比自锻弹丸被干扰后的偏转距离、破碎程度、侵彻能力等确定了线性聚能装药干扰自锻弹丸的最佳干扰角度。结果表明,线性聚能装药可以对自锻弹丸进行有效的干扰,其干扰角度对干扰效果有较大影响。在0°~90°范围内,干扰角度为60°时干扰效果最佳。
线性聚能装药;干扰;聚能射流;自锻弹丸;数值模拟;侵彻
引 言
通过附加装甲以增强坦克等武器系统战场生命力是目前防护技术中最重要的手段之一,爆炸反应装甲依靠炸药爆炸产生的爆炸场以及被炸药驱动的飞板干扰聚能射流和动能长杆弹[1-3],其基本结构为“钢板+炸药+钢板”的三明治式结构,但是爆炸反应装甲对自锻弹丸的防御效果不佳[4-5]。第5代爆炸反应装甲作为目前最先进的具有三防功能(防破甲,防穿甲,防串联战斗部)的爆炸反应装甲,线性聚能装药是其核心结构,主要依靠其爆炸形成的线性射流来干扰来袭射流以及长杆弹[6];李勇等[7]采用数值模拟的方法对线性聚能装药干扰长杆式动能弹进行了研究,并取得了良好的防御效果。但采用线性聚能装药干扰自锻弹丸方面,国内外尚未有文献报道。
本研究采用有限元软件ANSYS/ls-dyna对线性聚能装药以不同角度干扰来袭自锻弹丸以及自锻弹丸被干扰后侵彻45号钢板的全过程进行了动态数值模拟,通过分析对比后效靶板上的最大侵彻深度、弹坑数目等参数以确定线性聚能装药干扰自锻弹丸的效果以及最佳干扰角度,以期为解决自锻弹丸的防御问题提供参考。
1 数值模拟
1.1 模型的建立
自锻弹丸选取大锥角(150°)圆锥形药型罩,其开口直径40mm,药型罩厚度2mm,装药高度40mm,炸高200mm;线性聚能装药参数为:开口直径20mm,药型罩厚度1mm,装药高度30mm;靶板尺寸为100mm×50mm×50mm,其剖面图如图1所示,其中干扰角度(θ)分别选取0°、30°、60°、90°;当干扰角度(θ)为0°和90°时,线性聚能装药中心轴线与自锻弹丸轴线分别重合与垂直。
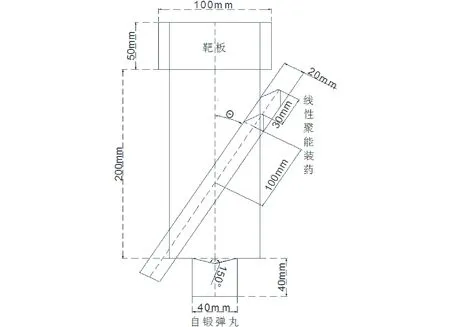
图1 线性聚能装药干扰自锻弹丸的数值模型剖面图Fig.1 Numerical model profile of interference the self forging projectile from linear shaped charge
1.2 材料模型的确定
自锻弹丸和线性聚能装药药型罩材料为紫铜,炸药为B炸药,靶板材料为45号钢。由于该模型具有对称性,因此在模拟线性聚能装药干扰自锻弹丸以及侵彻靶板全过程中建立1 /2 模型。整个模拟过程的数值模型为:炸药、药型罩、空气域和钢靶,其中炸药、药型罩、空气域为流体模型并采用Euler网格,钢靶为固体模型并采用Lagrange 网格。本研究中选择的数值模型的材料本构关系和状态方程如下:炸药采用HIGH-EXPLOSIVE-BURN 模型,状态方程为JWL;药型罩采用STINBERG模型,状态方程为GRUNEISEN;空气域采用无偏应力流体动力模型( NULL ),状态方程用GRUNEISEN 描述;钢板的模型采用随动塑性模型 (PLASTIC-KINEMATIC) 。
1.3 计算方法
采用ALE算法对线性聚能装药干扰自锻弹丸的过程进行数值模拟,采用流固耦合算法对被干扰后的自锻弹丸侵彻靶板的过程进行数值模拟。采用控制变量法,不考虑其他变量,只研究线性聚能装药对自锻弹丸因干扰角度的不同对干扰效果造成的影响。
通过Lsprepost 后处理软件分析自锻弹丸与射流头部相遇前、相遇过程以及自锻弹丸被干扰后侵彻靶板过程3个阶段的数值模拟结果。分析结果为:射流头部与自锻弹丸在68μs时刚好相遇,120μs时被干扰后的自锻弹丸开始接触靶板,200μs时被干扰后的自锻弹丸失去侵彻能力。
2 结果与讨论
2.1 射流头部与自锻弹丸相遇前的结果分析
根据模拟结果,在研究射流与自锻弹丸相遇前这一阶段时,观察60μs时的状态,如图2所示。
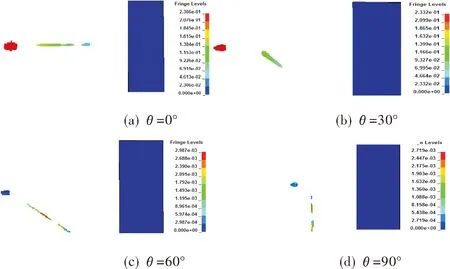
图2 60μs时线性聚能装药与自锻弹丸相遇前的效果图Fig.2 Impression drawing before meeting of linear shaped charge and self forging projectile at 60μs
当药型罩结构为大锥角(120°~160°)金属锥罩或曲率半径为1.00~2.36倍装药直径的球缺罩、双曲线罩时,炸药爆炸后形成的爆轰波作用于药型罩界面时形成自锻弹丸;药型罩锥角小于120°时形成射流。由图2可看到,60μs时自锻弹丸和射流尚未接触,此刻的速度可作为射流干扰自锻弹丸前的速度,测得此刻自锻弹丸速度为2020m/s,射流头部速度为3460m/s,尾部速度为670m/s。
2.2 射流头部与自锻弹丸相遇过程的结果分析
根据Lsprepost 后处理软件观察数值模拟过程,68μs时,自锻弹丸与射流头部开始接触;72μs时自锻弹丸与射流脱离接触,其效果图如图3所示。
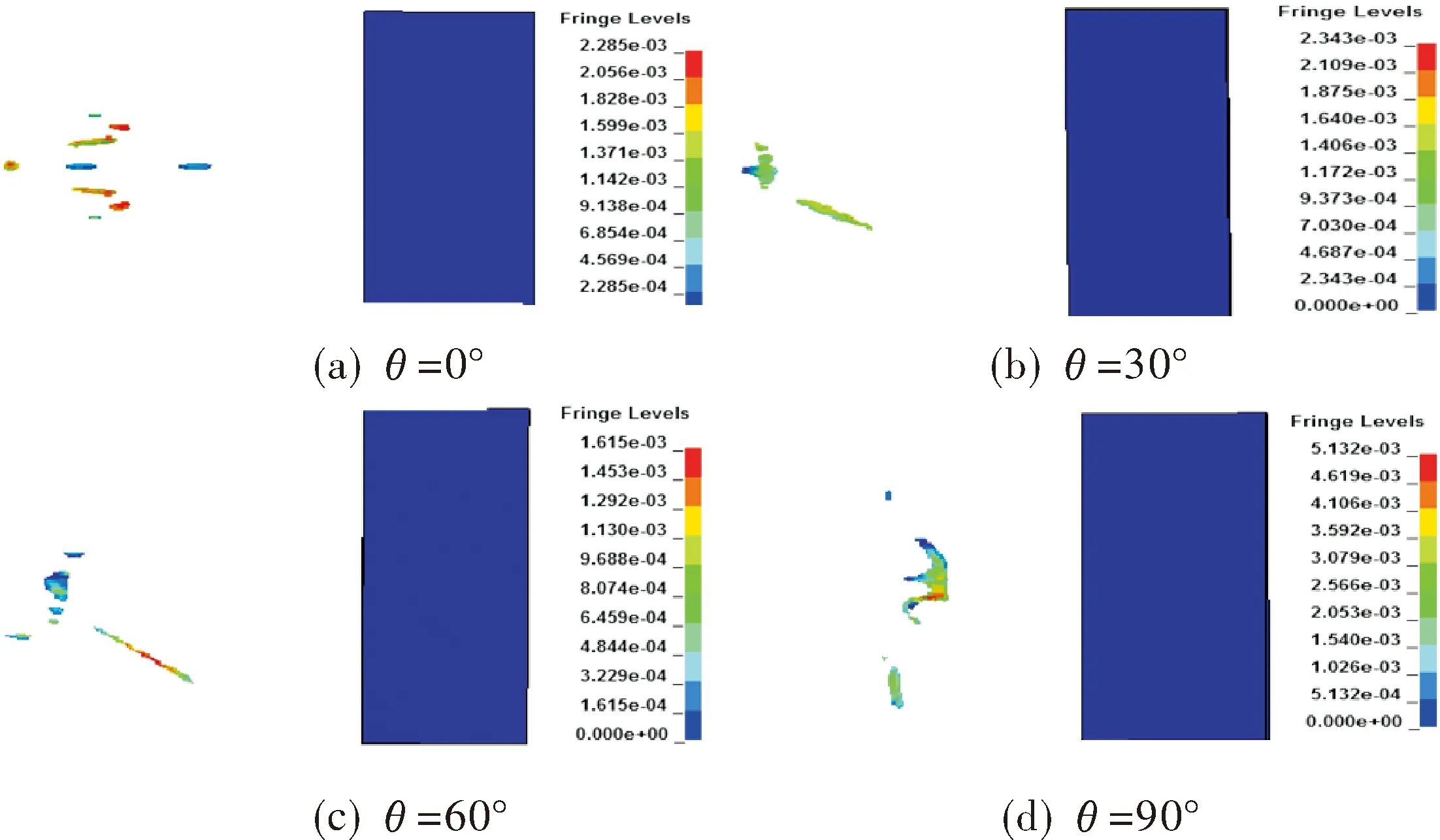
图3 72μs时自锻弹丸被线性聚能装药干扰后的效果图Fig.3 Impression drawing of after intercepting self forging projectile from linear shaped charge at 72μs
由图3可知,自锻弹丸与射流头部相遇时,由于二者均具有极高的速度以及自锻弹丸在形成过程中内部没有被完全压实,从而使自锻弹丸与射流相遇过程中发生破碎并产生大量碎片;且相遇过程中自锻弹丸在射流的干扰作用下还会偏离原有运动的路径(中心对称轴线)。由于线性聚能装药干扰自锻弹丸的角度(θ)不同,自锻弹丸的破碎程度和偏离程度也有一定的差异。直接分析破碎程度和偏离程度比较困难,因此本研究通过分析被干扰后的自锻弹丸开始侵彻靶板至失去侵彻能力这一时期靶板上的最大弹坑数目来说明自锻弹丸的破碎情况,分析最大侵彻深度偏离靶板轴线距离来说明自锻弹丸偏离中心轴线的程度。
2.3 自锻弹丸侵彻靶板过程的结果分析
自锻弹丸与干扰射流脱离接触后继续向前运动,在120μs时开始接触靶板,200μs时失去侵彻能力;在200μs时由于碎片间的相互影响其弹坑会发生重叠造成误差;通过观察后处理结果可知,在185μs时弹坑最为清晰,其效果图如图4所示。
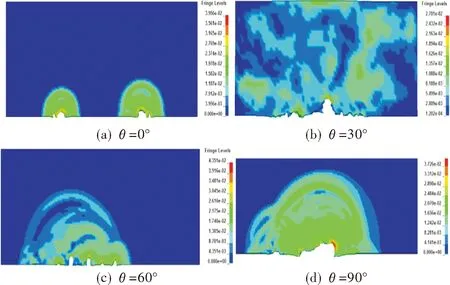
图4 185μs时自锻弹丸侵彻靶板的效果图Fig.4 Impression drawing of self forging projectile penetrating target plate at 185μs
由图4可知,靶板上的弹坑数目在干扰角度(θ)0°~90°内,θ越大弹坑数目越多,但θ接近90°时弹坑数目又随之减少;由此可知在θ为0°~90°内,随着θ的增大,自锻弹丸的破碎程度也随之增强,但θ接近90°其破碎程度将减弱。
在分析自锻弹丸偏离程度时,如果直接测量其偏离角度比较困难,因此,选择通过分析被干扰后的自锻弹丸在失去侵彻能力后在靶板上留下的最大侵彻深度的弹坑偏转中心轴线的距离来说明,通过后处理软件观察自锻弹丸在200μs时已经失去侵彻能力,其效果图如图5所示。
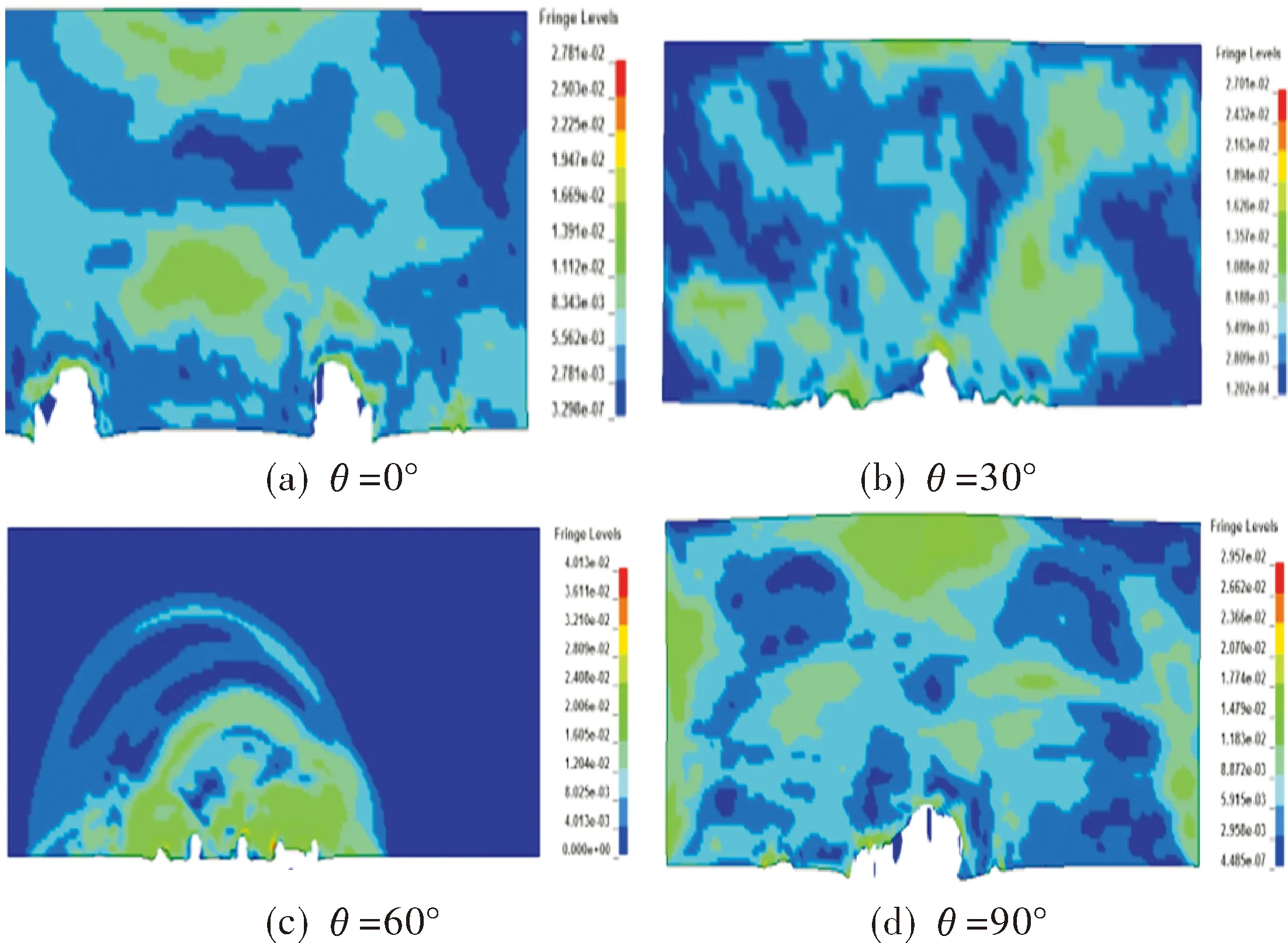
图5 200μs时自锻弹丸失去侵彻能力时靶板的效果图Fig.5 Impression drawing of target plate of loss of penetration ability of self forging projectile at 200μs
由图5可知,由于线性聚能装药对自锻弹丸干扰角度的不同,自锻弹丸被干扰后在侵彻靶板后靶板上的弹坑数目(n)、弹坑分布直径(D)、最大侵彻深度(h)、最大侵彻深度弹坑偏离靶板轴线距离(L)均存在一定的差异,测量200μs时靶板弹坑参数如表1所示。
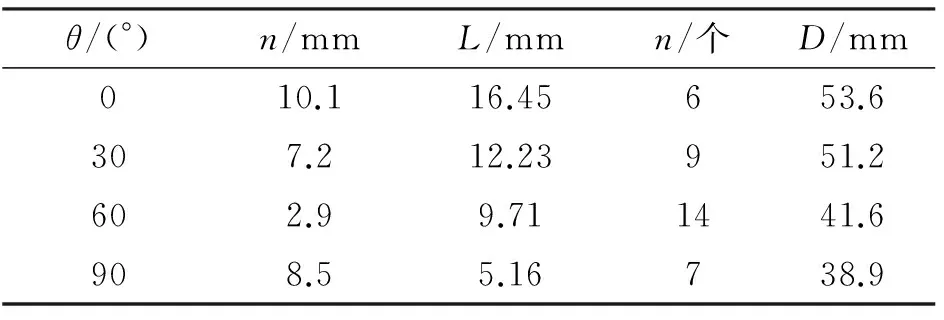
表1 200μs时的靶板弹坑参数
由表1可知,θ在0°~90°内,随着θ的增大,自锻弹丸被线性聚能装药干扰后最大侵彻深度减小,θ为60°时最大侵彻深度最小;随着θ的增大,被干扰后的自锻弹丸侵彻靶板最大侵彻深度偏离中心轴线的距离逐渐变小,靶板上的弹坑数目随着θ角的增大而增多,说明自锻弹丸的破碎程度随着θ角的增大而增强,但θ接近90°时其破碎程度降低;靶板上的弹坑分布直径随着θ的增大而逐渐减小,说明随着θ的增大,自锻弹丸被干扰后对靶板的影响范围变小。
因射流与自锻弹丸的接触时间极短,因此分析射流干扰自锻弹丸过程中可将射流假设为密度均匀、截面相等、速度为V的弹丸:根据模拟结果可知,θ为60°时,线性聚能装药对自锻弹丸的干扰效果最好。当θ为 60°时,线性聚能装药产生的射流与自锻弹丸相遇时可将其速度V分解为垂直于自锻弹丸中心轴线的方向速度V1和与自锻弹丸中心轴线平行速度V2(方向与自锻弹丸相反)两个方向,如图6所示。
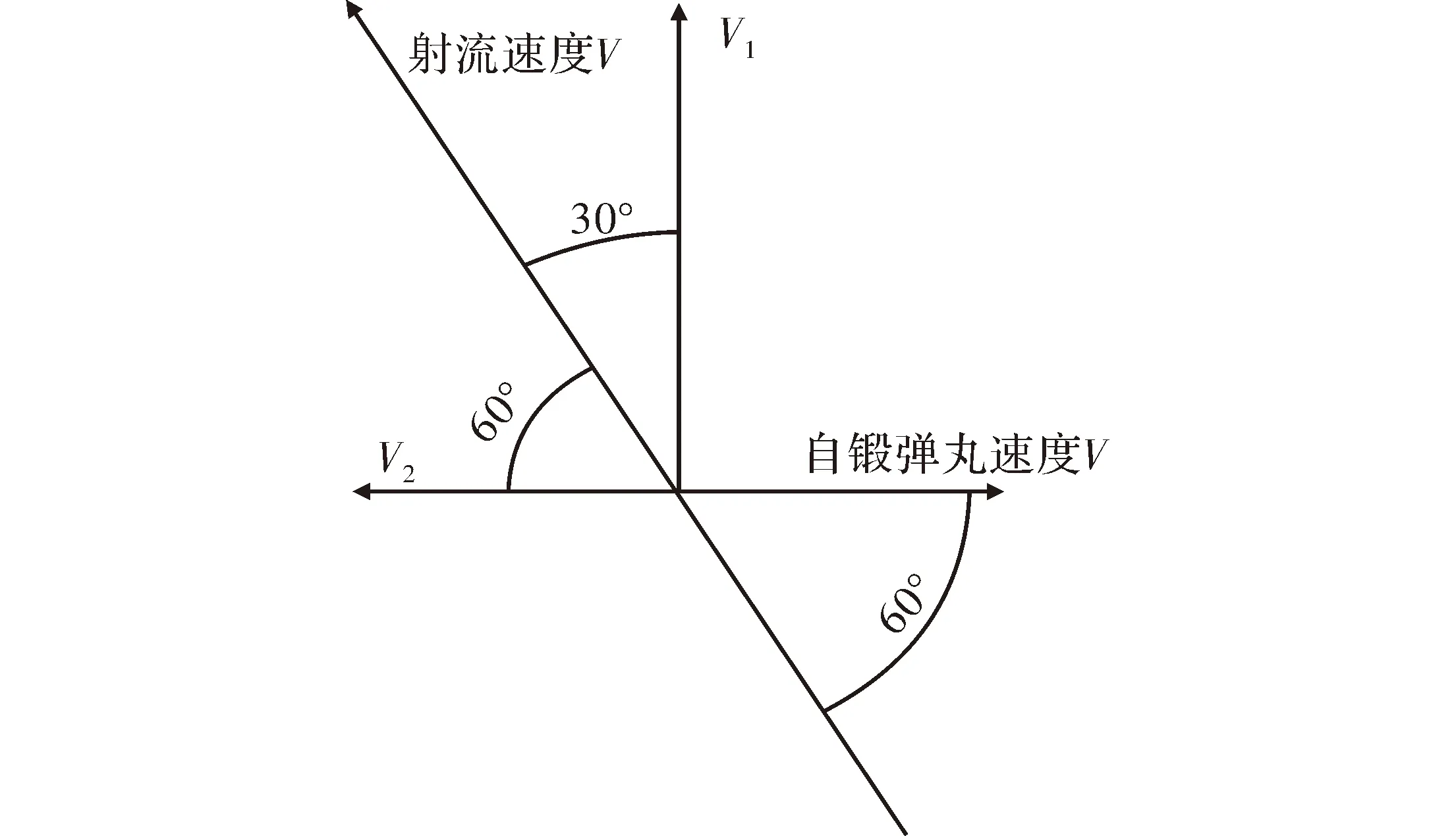
图6 射流速度分解图Fig. 6 Decomposition graph of jet velocity
比较θ为0°、30°、60°时射流的分速度(V1、V2)大小变化,当θ为 60°时,射流的分速度(V1)即与自锻弹丸运动路径垂直方向的速度最大,这说明在射流侵彻进入自锻弹丸内部后其垂直于自锻弹丸方向的能量最大,因此破碎程度较大,产生的碎片较多;当θ为90°时,虽然其垂直于自锻弹丸的速度(V1)最大,但是其与自锻弹丸平行且方向相反的速度(V2)为零,又因为射流速度(V)远大于自锻弹丸速度,在两者相遇时射流会瞬间以近似垂直于自锻弹丸中心轴线的方向将其穿透,因此其破碎程度也最低,干扰效果较差;由此也可得出,线性聚能装药干扰自锻弹丸的角度(θ)对自锻弹丸破碎程度有较大影响,而自锻弹丸的破碎程度直接影响其侵彻能力,进而验证了θ对干扰效果有较大的影响。
3 结 论
(1)采用数值模拟软件ANSYS/ls-dyna建立了数值模型,通过对自锻弹丸被不同干扰角度的线性聚能装药干扰后侵彻45号钢板的过程进行数值模拟,得出线性聚能装药可以有效地对来袭自锻弹丸进行干扰,其干扰效果与线性聚能装药的干扰角度θ有关。
(2)自锻弹丸在被线性聚能装药干扰后会发生破碎,其破碎程度与线性聚能装药的干扰角度θ有关。在0°~90°范围内,θ越大,自锻弹丸的破碎程度越大,但θ接近90°其破碎程度降低;自锻弹丸的破碎程度越高,其侵彻能力越低,干扰效果越好。
(3)在0°~90°内,θ越大,自锻弹丸被线性聚能装药干扰后对45号钢板的侵彻能力越强,当θ为60°时侵彻能力最弱,因此当θ为60°时干扰效果最好。
(4)自锻弹丸被干扰后会偏离原来的运动路径并且其产生的碎片仍然具有侵彻能力;自锻弹丸的偏离距离和在靶板上的分布范围随着θ的增大而减小。
[1] 王凤英. 装甲防护技术的发展[J]. 测试技术学报,2002(2):144-147. WANG Feng-ying.The development of armor fence[J].Journal of Test and Measurement Technology,2002(2):144-147.
[2] 李歌,王凤英,刘天生. 爆炸反应装甲干扰穿甲弹的试验研究[J]. 火炸药学报,2010,33(2):50-52. LI-Ge,WANG Feng-ying,LIU Tian-sheng.Experimental study on explosive reaction armor disturbing penetrators.[J].Chinese Journal of Explosives & Propellants(Huozhayao xuebao),2010,33(2):50-52.
[3] 董旭意. 反应装甲对射流的干扰机理研究[D].南京:南京理工大学,2008. DONG Xu-yi.Study on the interference mechanism of reactive armor to jet[D].Nanjing:Nanjing University of Science and Technology,2008.
[4] 戴广峰. 反应式装甲一席谈[J]. 现代兵器,1991(9):7-11. DAI Guang-feng.Brief introduction of armor[J].Modern Armament,1991(9):7-11.
[5] 王健,曹红根,周箭隆. EFP侵彻爆炸反应装甲过程研究[J].南京理工大学学报(自然科学版),2008(1):9-12. WANG Jian,CAO Hong-gen,ZHOU Jian-long.EFP penetrating explosive reactive armor[J].Journal of Nanjing University of Science And Technology(Natural Science Edition),2008(1):9-12.
[6] 焦丽娟. 新型反应装甲技术研究[D].太原:华北工学院,2001. JIAO Li-juan.Study on new technology of armor [D].Taiyuan:North University of China,2001.
[7] 李勇,刘天生. 线性聚能装药干扰杆式穿甲弹的数值模拟研究[J]. 工程爆破,2013(Z1):15-19,9. LI Yong,LIU Tian-sheng.Numerical simulation on the interference with rod penetor by linear shaped charge[J].Engineering Blasting,2013(Z1):15-19,9.
Numerical Simulation of Interference Self Forging Projectile from Linear Shaped Charge
RUAN Guang-guang,WANG Feng-ying,YUE Ji-wei,SHI Jun-lei
(School of Environment and Chemical Engineering,North University of China, Taiyuan 030051,China)
To study the effect of linear shaped charge on the interference of self forging projectile at different angles, the whole process of interference self forging projectile from linear shaped charge at different angles (0°、30°、60°and 90°) and penetrating into No.45 steel plate after the self forging projectile was intercepted was numerically simulated by finite element software ANSYS/ls-dyna.The three stages of physical change in the process of penetrating the No.45 steel plate of self forging projectile with the jet head of shaped charge before meeting, meeting process and after meeting were analyzed through the Lsprepost postprocessing software. The optimum interferencing angle of interferencing the self forging projectile from linear shaped charge was determined through the comparative analysis of deflection distance, broken degree, penetration ability etc. after the self forging projectile is interference.The results show that the linear shaped charge can effectively interfere with self forging projectile, and the interference angle has a great influence on the effect of interference. In the range of 0° to 90°, the effect of interference is best when the interference angle is 60°.
linear shaped charge; interference;shaped jet;self forging projectile; numerical simulation;penetration
10.14077/j.issn.1007-7812.2017.02.014
2016-09-25;
2016-12-05
国家自然科学基金(No.11572292)
阮光光(1990-),男,硕士研究生,从事战斗部设计研究。E-mail:rggjiayou@163.com
TJ55;O38
A
1007-7812(2017)02-0075-04
