圆周运动中临界位置不在最高点——一道模拟题引发的思考

安徽省太和中学(243173) 孙恒启●

安徽省当涂县石桥中学(243173) 麻继安●



圆周运动中临界位置不在最高点
——一道模拟题引发的思考

安徽省太和中学(243173) 孙恒启●

安徽省当涂县石桥中学(243173)
麻继安●

衡水中学2016-2017学年度上学期高三年级三调考试物理试卷第14题是一道选择题：

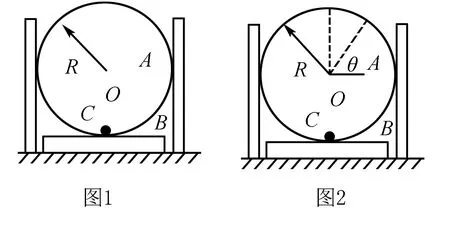
原题 如图1所示，A是半径为R的圆形光滑轨道，固定在木板B上，竖直放置；B的左右两侧各有一个光滑挡板固定在地面上，使其不能左右运动，小球C静止放在轨道最低点，A、B、C的质量相等.现给小球一水平向右的初速度V0，使小球在圆形轨道的内侧做圆周运动，为保证小球能通过轨道的最高点，且不会使B离开地面，初速度V0必须满足(g为重力加速度)( ).

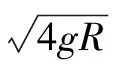
命题者所给的参考答案是B、D.

仔细研究会发现，该题应是一个单选题，答案应为B.而类似的问题在其他调研卷中同样存在，考查结果发现绝大部分学生也出现同样的问题.因此，很有辨析指正的必要.

失误探因 根据命题者所给的参考答案推测，其解题思路可能是：

设小球质量为m，运动至上顶点时的速度为V1，轨道对小球的压力为N，小球对轨道的弹力为N'，由机械能守恒定律可得：

在最高点由向心力公式可得：

由牛顿第三定律可得：N=N′

根据题意对轨道进行受力分析可得：

0≤N≤2mg

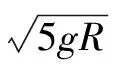
故答案为B、D.

错误诊断 本题在求V0的最大值时，是利用小球在轨道的最高点时小球对轨道的弹力等于2mg，也就是说认为小球在轨道最高点时对轨道的弹力的竖直分力最大，但是，事实真的如此吗？弹力竖直分力的最大值真的在轨道的最高点取得吗？

正确思路 设小球质量为m，其运动到与水平方向夹角为θ时速度为V2，轨道对小球的压力为N，小球对轨道的弹力为N′，由机械能守恒定律可得：

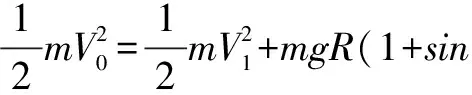
在最高点由向心力公式可得：

由牛顿第三定律可得：

N=N'

联立以上三式可得：

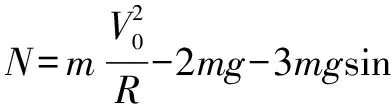
弹力的竖直分力为：

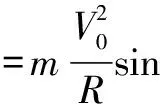
而Nsinθ≤2mg

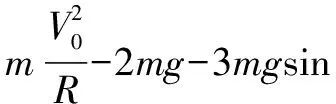
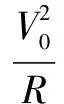
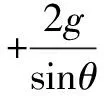
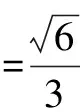
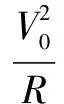
拓展延伸 不妨令圆形光滑轨道与木板B的总质量为M，那么上述问题就是M=2m的情况，那么M=m，M=3m，M=4m又是什么情形呢？如图2.

如图3，由数学知识可知该对勾函数在第一象限的图像大致为：

图3

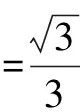
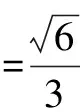
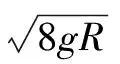
图4

同类链接 (改编)如图4所示，装置是足够长的光滑水平面，水平面上有一光滑的竖直圆环轨道，圆环轨道与水平面光滑对接但不固定，圆环轨道水平直径的左右两侧由光滑支柱P和Q能够控制轨道只能向上运动，圆环轨道的质量M=1.0kg，一质量为m=0.5kg的小滑块以初速度为5m/s从水平面上开始向右运动，g=10m/s2．求：若小滑块不脱离圆环轨道且圆环轨道不离开水平面，求圆环轨道半径的取值范围.

解 由题意可知，小滑块第一次经过竖直圆环轨道不脱离圆环轨道且圆环轨道不离开水平面，以后都不会实现分离，只需分析滑块第一次经过圆环轨道的情况就可以了.进入圆轨道不脱离圆轨道的条件有两种情况，下面分别讨论：

Ⅰ.物块上升到与圆心等高处时速度为零，物块将返回运动，且圆轨道不会离开地面.由机械能守恒定律有：

解得R=1.25m，故不脱离圆的条件是R≥1.25m.

Ⅱ.物块上升能通过圆轨道的条件是在轨道最高点：

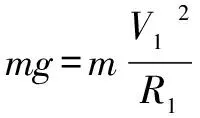
解得R1=0.5m

②当物块上升到圆心等高点以上的某一点时，设物块与圆环导轨间的作用力为N，此时物块速度为V2，令在圆环最低点时的速度为V0，由机械能守恒定律得：

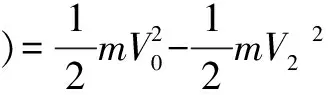
Nsinθ≤Mg

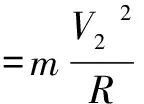
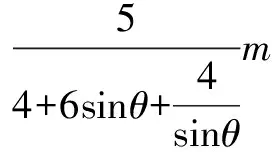
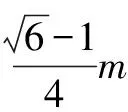
由此不难看出，在圆周运动中圆轨道的最高点未必是竖直分力最大的位置，而有些问题在这方面的解析避繁就简，有失准确性.

G

B

1008-0333(2017)10-0078-02