还原三视图的神奇宝盒

浙江省宁波市慈溪实验高级中学(315300) 俞 健●



还原三视图的神奇宝盒

浙江省宁波市慈溪实验高级中学(315300)
俞 健●

三视图是新教材引进的一个新内容，考查难度在逐年递增.其中关键的难点在于如何能把三视图还原成空间几何体.无论你如何远看成岭侧成峰，远近高低各不同，其实我们所有的问题都可以用一个万能长方体解决.

高中数学;三视图;还原

首先我们应该运用逆向思维，从出题者的角度看问题.出题者先确定空间几何体，再画出其三视图，要求考生根据已给出三视图，解答问题.而出题者所给出的所有空间几何体都必定是某长方体中的一部分.通过不同的割补手法，通常有常规式、切角式和组合式这三种空间几何体.

一、常规式——先定底再定头(常规几何体)

三视图刚出现的几年，出题者往往选择一些“普通”的锥体和柱体，最常见的就是三棱锥、四棱锥.给出一个最“简单”的摆放位置，给出三视图让我们还原，我们可以根据三视图的长、高、宽绘制一个能包住该空间几何体的长方体盒子，根据俯视图确定底面，再根据其他两个视图估计是锥体还是柱体，若是柱体，由俯视图在长方体的上表面确定上底面，从而得出结论；若是锥体，则由俯视图在长方体的上底面确定顶点.

而最近几年慢慢出现的变化是“普通”几何体的“不普通”放法，我们先定的底可能是由侧视图或正视图，把“普通”的几何体“放倒”，其实解题的策略还是一致的.

例1 若某几何体的三视图(如右上图)所示，则这个几何体中最长的棱长等于____，体积等于____.

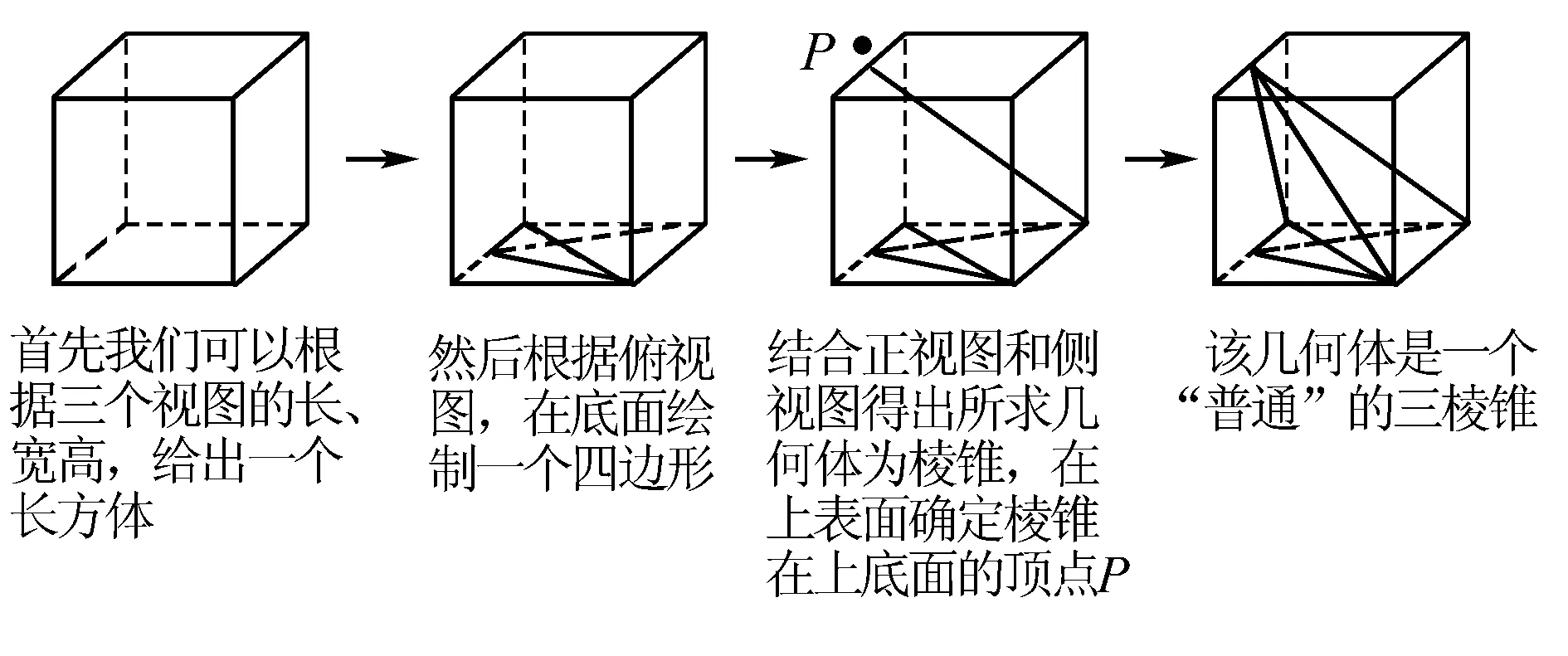
变1 根据右面的这个多面体的三视图画出其直观图

思路分析

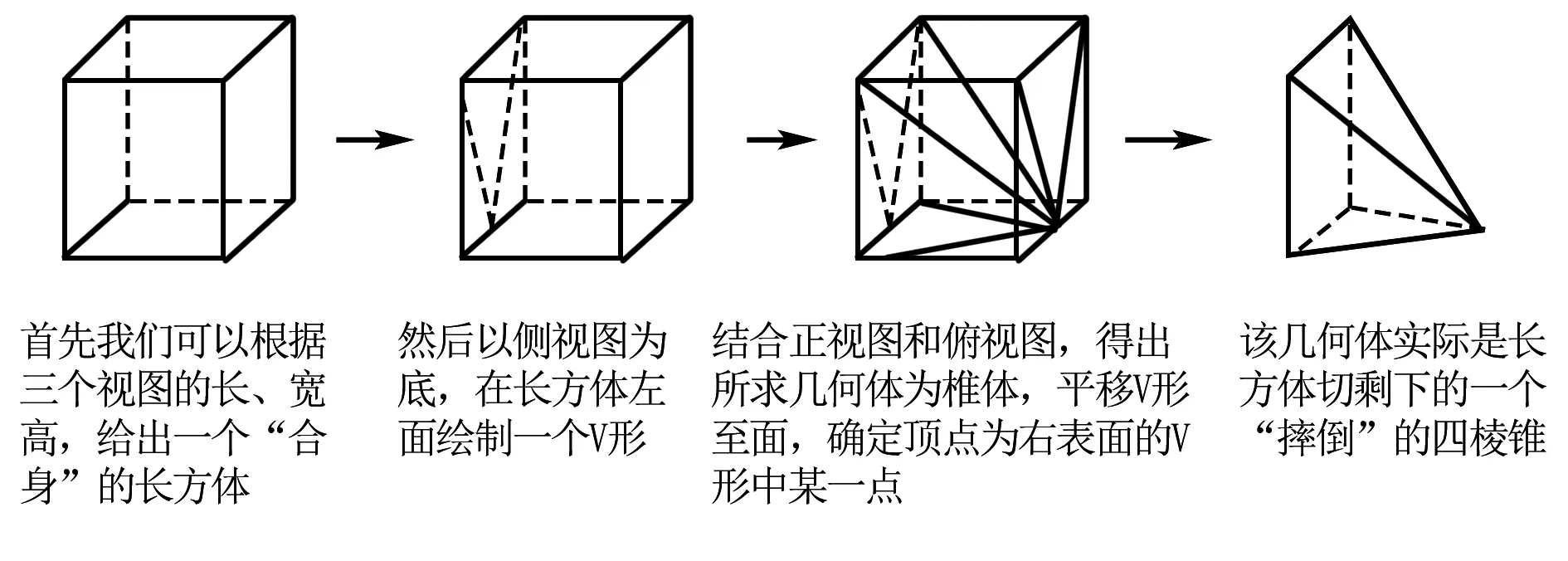
点评 不是所有图形都是从俯视图入手的.我们还原“普通”几何体时首先要确定的是该几何体的底，分成下上、左右、前后三类，左右和前后的顺序可根据线段的虚实确定.

二、切角式——长方体切掉简单几何体

这类几何体往往是从长方体中切去若干个“普通”锥体与柱体，剩下一个不规则几何体或者不规则放置的“普通”几何体.这类问题出现，往往让考生不能根据某个底，迅速想像出几何模型，那我们就要抛弃这个复杂的结果，考虑几何体形成的过程，简单—简单 = 复杂，回避问题的复杂性.

例2 根据下面这个多面体的三视图画出其直观图

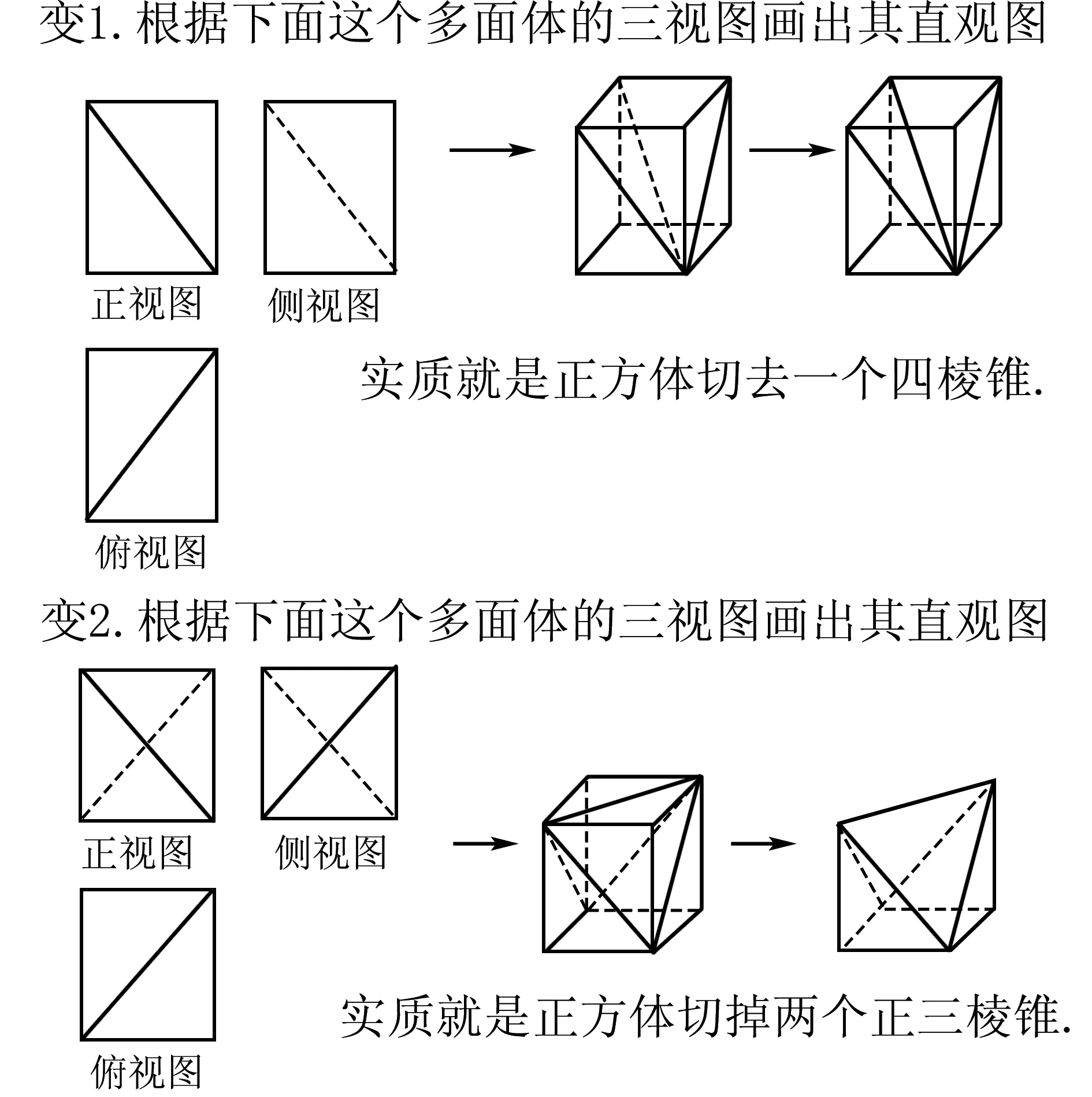
点评 其实在某种情况下，由三视图得出的直观图并不一定唯一,其实这种图形的变化也多种多样，我们在长方体周边切掉的三棱锥或四棱锥也可以在缩小到原棱长的一半，三分之一等等，这类问题的空间几何体原型是最简单的长方体，而切掉的也是常见的比较简单的几何体，对考生而言，都是比较熟悉和可以想象的，可这样：简单减去简单的过程之后，剩下的几何体则是我们日常生活和教学过程中不常见的几何体或者是“悬空”放置的一些几何体.所以，一旦我们遇到一眼不能快速想像“普通”几何体的问题，往往可以考虑这种切边角料的思路.

三、混搭式——简单几何体的组合

这类几何体往往是几种常见的几何体的一个组合，直观性比较强，我们也可以先给这个几何体定好包围在外的长方体，然后把常见的柱锥台组合猜想在一起.

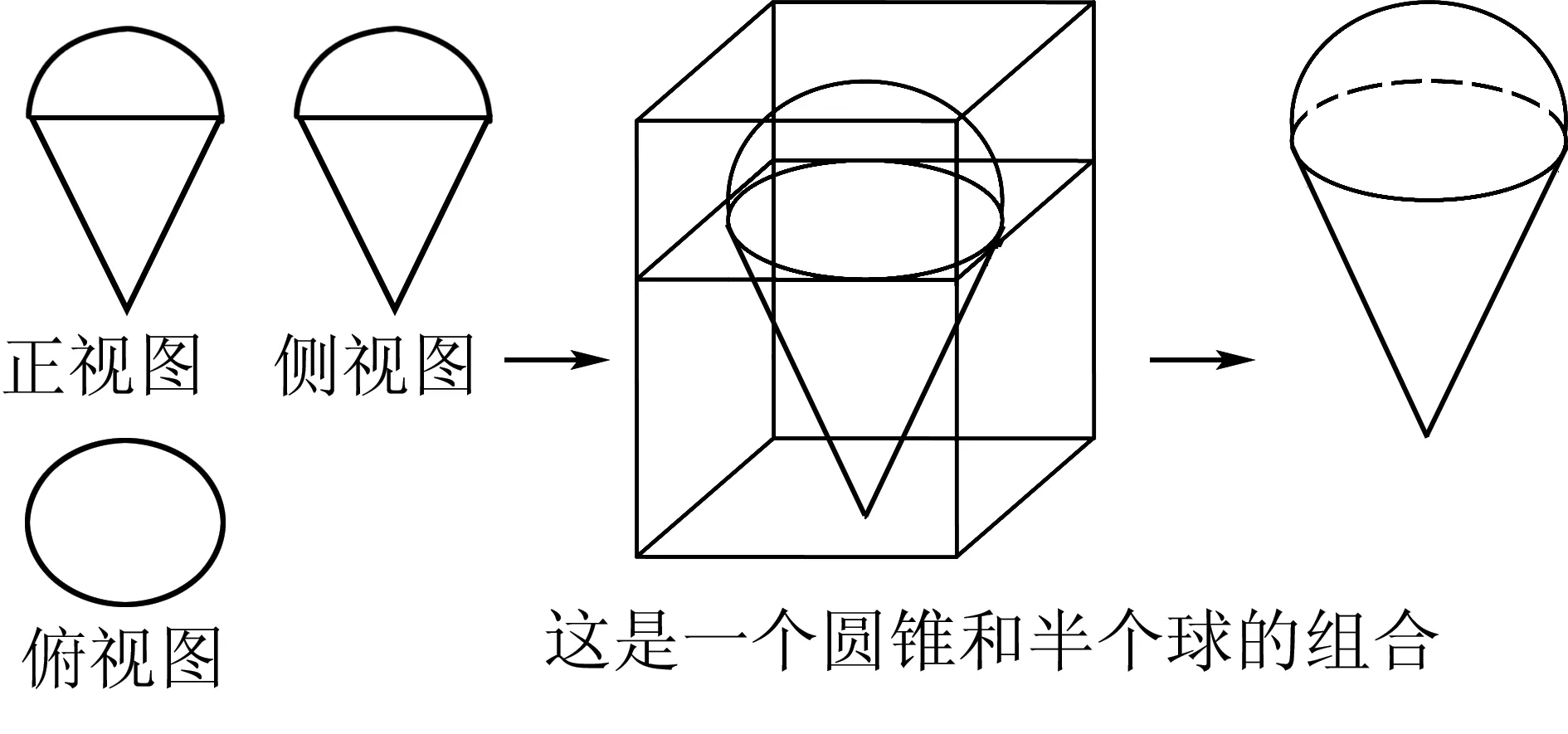
例3 (课本P15练习2)根据下面这个多面体的三视图画出其直观图如下图.

其实这个图形的组合还有很多，比如圆锥与圆柱，圆锥与棱柱，棱锥与圆柱，棱锥与球，圆柱与棱柱等等.出题者一般肯定是在棱柱、棱锥、棱台及圆柱、圆锥、圆台这6中常规几何体中选择2种或3种进行一个组合，明白出题者的命题方向，那么我们解题就能知己知彼，战无不胜.

解决了三视图的还原问题，那么接下来几何体的表面积，体积等等问题都可以迎刃而解，该问题较能体现学生的空间想象能力和学生对空间几何体的认知水平，而突破这个问题的关键就是要把所有的问题化归到学生非常熟悉的生活模型中，所以笔者从一个万能长方体入手，把所有几何体原型都装入这个万能盒子中，通过自下而上(或自左往右、自前往后)、简—简、简+简的三种构造方式来考虑问题，最后再用长方体的3个表面为底，验证构造的成功与否.有了这个长方体的“依靠”，三视图问题再也不是碰运气，而是有法可依.

G632

B

1008-0333(2017)10-0037-02